超阈值模型中时域外推GPD估计方法选择
2021-09-16王普长陈晋市张淼淼何春晖
王普长,孙 辉,陈晋市,张淼淼,何春晖
(1.江苏徐工工程机械研究院有限公司,江苏 徐州 221000; 2.吉林大学 机械与航空航天工程学院,吉林 长春 130025)
引言
近年来,随着工程机械行业的发展,我国逐渐推进国产零件从高产到高质的转变;而国产工程机械可靠性差,适用性不强的问题亟需解决。因此,我国大力支持可靠性领域的研究,推动可靠性理论研究的发展。载荷谱是整机零件在典型工况下所受载荷的时间历程,经数学方法处理后,得到其典型载荷的概率频次特征[1-2]。编制载荷谱可以通过极少的试验样本获得大量的样本数据[3],节约了时间和人力成本,为后续的台架加载提供原始样本,是可靠性研究的重要环节[4-5]。
载荷谱最初是针对航空航天领域提出的,经过数十年的发展,其研究范围已超出航空航天领域[6],早已应用至汽车、工程机械、机床等领域[7]。载荷谱外推分为雨流域外推与时域外推,时域外推中主要方法是极值外推法;极值外推法的主要思想就是将对零件损伤产生主要贡献的载荷进行预测。一般认为,超越量服从广义帕累托(GPD)分布。极值外推法的目的,就是寻找与GPD分布拟合最接近的阈值。因此,准确的参数估计方法,将数据对广义帕累托分布进行拟合,是极值外推重要环节之一。
针对拟合结果,国内外许多学者展开了大量研究:沙雪云等[8]分别将贝叶斯与极大似然估计法进行拟合,并对比拟合结果,得到拟合更好的方法;李景奎等[9]提出一种改进极大似然估计法,对3参数威布尔分布进行拟合,并将该理论应用到民航维修,为民航企业合理制定维修计划提供了理论依据;DANESHI N等[10]同样对极大似然估计进行改进,并利用到实际应用中,证明改进模型的可行性。
在可靠性方面的研究中,国内外许多学者对试验数据的处理进行探索:王蓉华等[11]提出逆L-矩估计,应用到疲劳寿命分析中,并与其他常用参数估计法进行对比,验证其方法的准确性;MUSSIE T等[12]提出一种新的寿命分布模型,利用矩估计与极大似然估计法进行拟合,最后用试验数据进行验证;崔策等[13]采用3参数Weibull分布对大型风机液力变桨系统失效率估算结果,表明3参数Weibull分布适应性更高;YIN F L等[14]基于极大似然估计法估计3参数Weibull分布,提出一种新的参数估计模型,实现更为精确的参数估计,并应用到轴承寿命分析中。
基于以上研究,常认为超阈值样本的分布服从GPD分布。本研究详述了3种最常用的用来拟合广义帕累托分布的参数估计方法,最大似然估计法、矩估计法及概率权矩估计法,其过程如图1所示。总结了不同参数估计方法的过程及注意要点,对比不同参数估计方法的拟合曲线及相关系数,并进行对比找出最优方法。
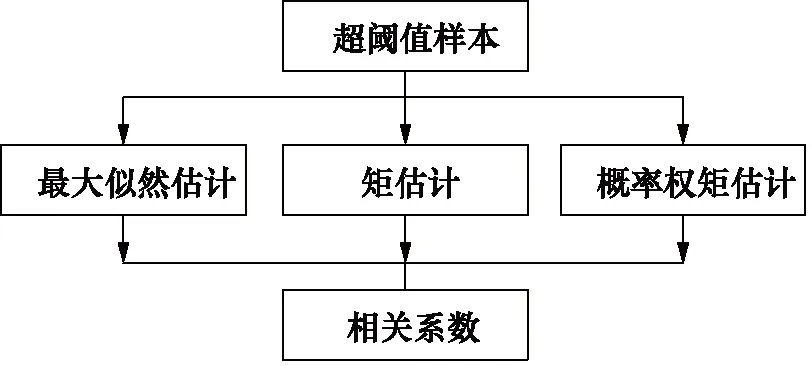
图1 参数估计过程Fig.1 Parameter estimation process
1 GPD分布
时域极值外推法的思想关键在于研究超越量的函数分布式,并由函数式随机生成新的样本点。
根据李昕雪等[15]研究表明,通常对于阈值较大的样本,超越量服从分布GPD。
GPD累计函数表达式为:
(1)
概率密度表达式为:
(2)
式中,z=xi-μ(i=1,2,3,…,n)为样本超越量;μ为阈值;σ为尺度参数;ξ为形状参数。
2 参数估计
2.1 最大似然估计(ML)
设x1,x2,…,xn为一组符合GPD分布的超阈值样本,根据GPD分布函数得到相应的对数似然函数为[16]:
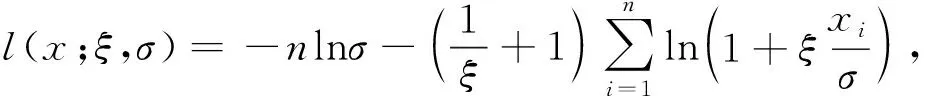
ξ≠0
(3)
式(3)分别对σ和ξ求偏导得:
(4)
令偏导数等于0,并联立方程组,解得:
(5)
通过式(5)可以解得参数σ和ξ。
2.2 矩估计(MoM)
MoM是由PEARSON提出的一种参数估计方法,根据辛钦大数定律可知,简单随机样本的原点矩依概率收敛于相应的总体原点矩,用样本矩代替总体矩,进而计算出未知参数的估计值。
设x1,x2,…,xn为一组符合GPD分布的超阈值样本,由式(2)得:
(6)
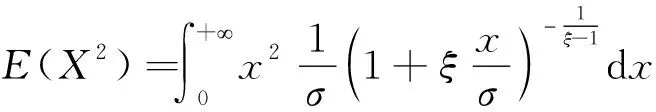
(7)
式中,E(X)和E(X2)分别表示超阈值样本的期望和二阶矩,σ和ξ分别表示尺度参数和形状参数。
根据式(6)及式(7)可得:
(8)
式中,D(X)表示超阈值样本的方差。
用样本的各阶矩替换总体的各阶矩,可得到σ和ξ的矩估计,即:
(9)
式中,E(X)和D(X)分别为样本的均值和方差。
2.3 概率权矩估计(PWM)
矩法的一般原则是让所研究的总体分布的各阶矩与对应的样本矩相等,但是样本的二阶及高阶样本矩抽样性质不好,因此引入一种新的矩估计方法,即概率权矩估计,设x1,x2,…,xn为一组符合GPD分布的超阈值样本,其公式如式(10):
ωn(θ)=E[XFn(X;θ)],n∈N0
(10)
将GPD函数代入到式(10)中,得到GPD分布的n阶概率权矩估计公式,如式(11):
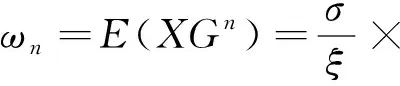
(11)
为估计GPD分布中参数σ和ξ的值,分别令n为0和1,得到相应的零阶和一阶概率权矩,并用样本概率权矩代替总体概率权矩得到参数估计:
(12)
式中,σ和ξ分别表示尺度参数和形状参数。
3 实例分析
3.1 载荷谱数据采集
柱塞泵是影响挖掘机挖掘性能的重要部件[17]。本实验以某公司20 t级反铲液压挖掘机为研究对象,测试场地为原生土场地且原生场地土壤不低于III级。
为方便驾驶人员操作及试验人员采集,本研究利用无线信号传输装置远程采集试验数据,原理如图2所示。

图2 压力传感器监测原理图Fig.2 Schematic diagram of pressure sensor monitoring
本试验主要测量挖掘机挖掘期间,主泵出口压力载荷的时间历程。为了方便后续数据处理及工况分割,还同时监测其他参数,如在油缸处安装压力传感器和线位移传感器,在发动机处安装转速传感器,监测油箱油位等。本试验采用松散土砂作为挖掘物料展开试验,挖掘现场如图3所示。

图3 物料挖掘现场Fig.3 Material excavation site
挖掘机工作环境恶劣,在进行数据采集时不可避免的会存在奇异点,因此本研究利用小波分析对采集的载荷谱进行数据降噪及去除奇异点处理,处理后的载荷时间历程如图4所示[18]。
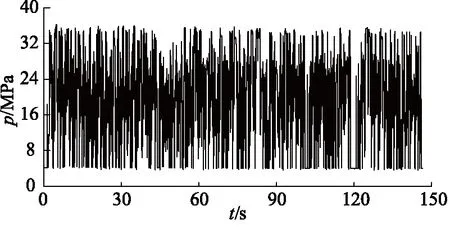
图4 挖掘机主泵出口压力Fig.4 Excavator main pump outlet pressure
3.2 参数估计
为了提高计算效率,将预处理后的数据按升序进行排列,选取该组数据中间位置的数值Z1和98%分位点处的数值Zm构成n个备选阈值[19]。利用上述3种方法,计算出各备选阈值所对应的GPD分布拟合参数,并以每种参数估计方法中各备选阈值所对应的GPD分布与超阈值样本之间的最小均方误差所对应的值作为最优阈值[20]。再通过对比各最优阈值的GPD分布和超阈值分布的CDF图,找到其中最优的参数估计方法。
根据测试挖掘机主泵载荷谱数据,计算出Z1=203,Z1420=344.9,分别用上述3种参数估计方法计算出1420个阈值所对应的最小均方根误差,得到各备选阈值和均方根误差之间的关系如图5所示。
根据图5所示各备选阈值u和均方根误差关系,可得最小均方根误差所对应的阈值,并选取载荷谱中最优阈值以上的数据,通过3种参数估计方法进行GPD分布拟合,得到3种估计方法所对应的最优阈值及GPD分布的参数估计结果,如表1所示。
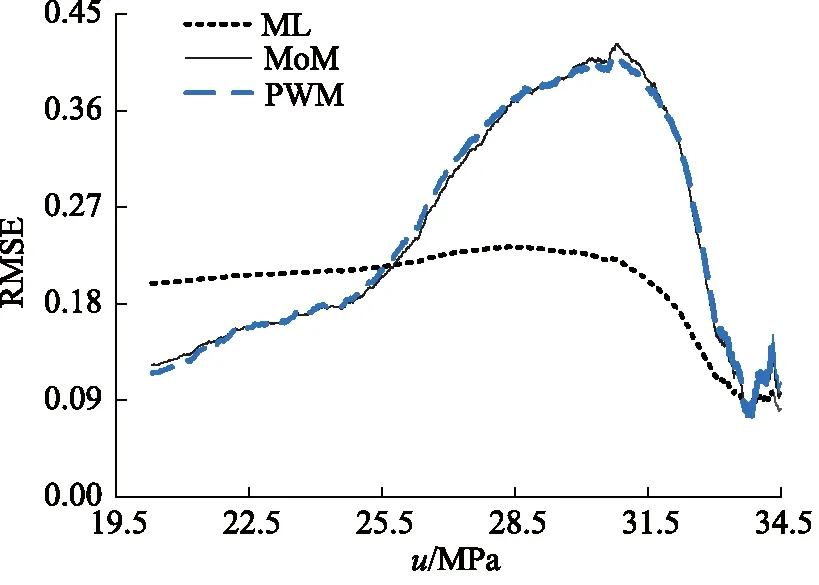
图5 备选阈值和均方根误差关系Fig.5 Alternative threshold and root mean square error relationship
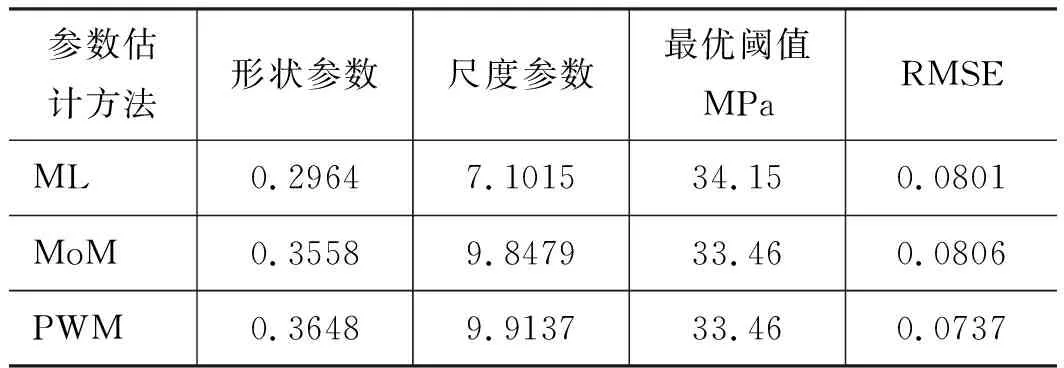
表1 GPD分布的参数估计结果Tab.1 Parameter estimation results of GPD distribution
为更加直观地反映每种GPD分布参数估计方法的优劣,分别绘制ML、MoM及PWM 3种参数估计方法拟合的GPD分布函数的累积分布频数图,如图6所示。
3.3 结果分析
由表1可知,ML参数估计方法所选的最优阈值较大,导致较多有效载荷数据丢失,MoM参数估计方法计算的最优阈值和PWM参数估计方法的最优阈值相同,但PWM参数估计方法的最小均方根误差略小于MoM参数估计的结果。累积分布函数P,根据图6可知,ML、MoM及PWM 3种参数估计方法所得到的样本值和拟合值之间的相关系数分别为0.9966,0.9971及0.9982,均大于0.99,因此3种参数估计方法均可以较好地拟合挖掘机主泵压力超阈值样本的GPD分布。相比于PWM参数估计方法,当超阈值样本数据小于1 MPa时,ML参数估计方法得到的CDF拟合图与超阈值样本载荷之间略大,当超阈值样本数据介于1~1.8 MPa之间时,MoM参数估计得到的CDF拟合图与超阈值样本载荷的CDF图之间差异略大。从图7可知,理论值u1、观测值u2,当超阈值样本数据大于8 MPa,ML参数估计的Q-Q图数据点偏离拟合直线,而MoM和PWM参数估计方法数据点均匀地分布在直线两侧,超阈值样本数据介于2~2.2 MPa之间时,PWM参数估计的Q-Q图偏离程度小于MoM参数估计。因此根据图6和表1可得,PWM可以作为挖掘机主泵超阈值样本GPD参数估计的最优选择。
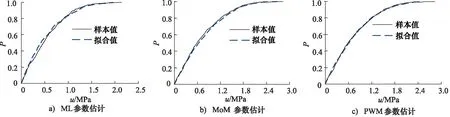
图6 最优阈值拟合CDF图Fig.6 Optimal threshold fitting CDF graph
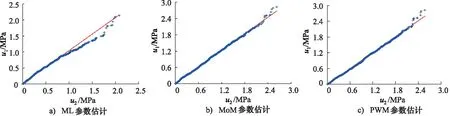
图7 最优阈值拟合Q-Q图Fig.7 Optimal threshold fitting Q-Q diagram
4 结论
本研究以最小均方根误差为检验准则,首先分别利用3种参数估计方法分别计算挖掘机主泵载荷谱POT模型的最优阈值和超阈值样本数据的GPD拟合参数,其次分别绘制超阈值样本数据及GPD分布的CDF图,得出以下结论:
(1) 极大似然估计、矩估计及概率加权估计所得到的参数均可以较好地拟合超阈值样本数据;
(2) 通过极大似然估计得到的最优阈值相对于矩估计和概率加权估计略大,会造成较多有效载荷数据的丢失;
(3) 概率加权估计得到的最优阈值可以保留较多的有效载荷信息,且通过概率加权估计方法得到的GPD分布与超阈值载荷样本之间的拟合更好。
