二阶可微型线对涡旋压缩机性能的影响
2021-09-16方占萍许世鹏
方占萍,许世鹏
(1.酒泉职业技术学院 新能源工程学院,甘肃 酒泉 735000;2.甘肃省太阳能发电系统工程重点实验室, 甘肃 酒泉 735000)
引言
以腔体容积变化为工作原理的涡旋压缩机因具有排量大[1]、性能高、结构紧凑、可靠性高等诸多优点被广泛应用在制冷和空调等领域[2-3],并随着研究的深入,其应用已拓展到涡旋增压器、涡旋泵、涡旋膨胀机等领域[4-6]。涡旋型线作为涡旋压缩机设计的基础,其设计方法是决定涡旋压缩机整机性能的根本因素。
目前涡旋型线的设计方法主要有等截面设计法和变截面设计法。等截面设计法采用1条解析曲线,因其固有特点,数学描述简单,加工较为方便,但压缩比较低且毛坯材料的利用率不高。在等截面型线设计中,吴臻等[7]采用基圆渐开线构建了动静涡旋盘,并建立了动静涡旋盘相啮合的三维流场数值模型;陈玉坤等[8]建立了等截面涡旋压缩机工作腔的几何模型,对工作腔中的气体流动进行了数值模拟;李超等[9]在多载荷耦合作用下,对等截面涡旋压缩机动涡旋盘的应力应变进行了深入分析。相对于等截面设计法,变截面设计法采用2条及以上曲线,虽然数学表述比较复杂,但能通过较少的圈数实现高的压缩比,同时还能充分利用毛坯材料,因此变截面设计法成为了研究的热点,得到了国内外相关学者的广泛关注。AHMAD等[10]利用建立的涡旋型线几何模型,模拟了涡旋盘在压缩过程中的运动变化;郝胜利等[11]建立了电动车空调用变壁厚涡旋压缩机的型线方程,并对其容积性能、动力性能和热力学性能进行了分析计算;刘国平等[12]利用有限元分析法对建立的涡旋型线几何模型进行了动态温度场分析;彭斌等[13]利用基圆渐开线-高次曲线-圆弧的组合形式建立了变截面涡旋压缩机的数学模型并对其开展了试验研究;王君等[14]采用全啮合涡旋型线的设计方法,建立了一种新型的全啮合变截面涡旋齿;侯才生等[15]利用Frenet标架对变截面涡旋型线进行了深入分析。这些研究极大地推动了涡旋压缩机变截面型线设计法的发展,但研究中均未涉及变截面型线在连接点处是否二阶可微的问题,而二阶可微与涡旋型线的光顺密切相关,从而直接影响涡旋压缩机的综合性能。因此有必要对变截面型线的二阶可微进行深入研究,进而尝试改进变截面型线的设计方法,提高涡旋压缩机的整机性能。
本研究基于涡旋型线设计理论,建立二阶可微变截面涡旋型线的容积模型和动力学模型,并在实际工况参数下,对涡旋型线的容积性能和作用在动涡旋上的气体力进行模拟分析,且与传统一阶可微型线进行对比,为涡旋压缩机变截面型线设计与方法研究拓宽了思路。
1 几何模型的建立
1.1 基线方程
图1为变截面涡旋压缩机型线的基线图。该基线由2段基圆渐开线和1段高次曲线构成,并且是按照基圆渐开线、高次曲线、基圆渐开线的顺序依次将3段曲线在连接点φ1和φ2(φ3)处连接,各段曲线的基线方程表示为:
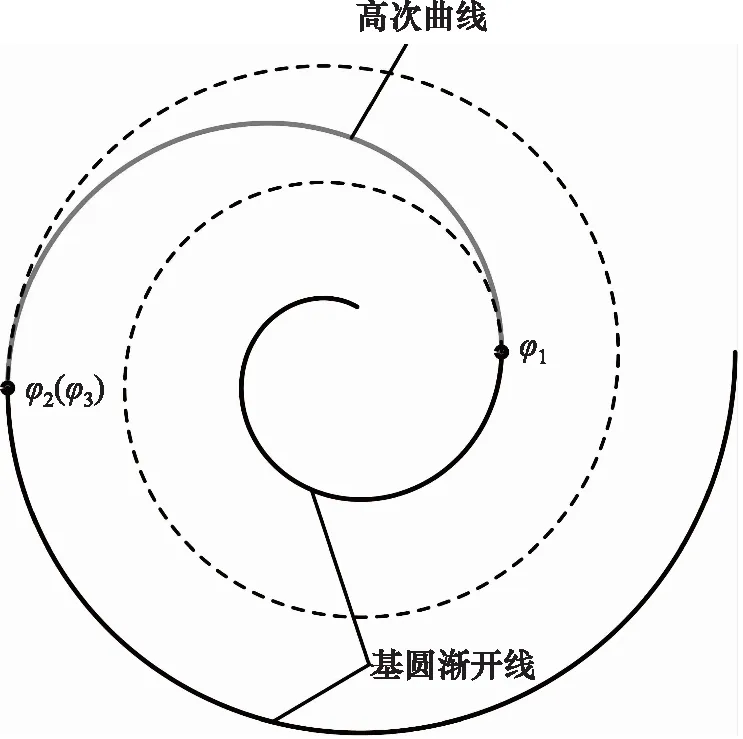
图1 涡旋型线的基线
第1段基圆渐开线方程:
(1)
式中,a—— 基圆半径
φ—— 型线的切向角
第2段高次曲线方程:
(2)
式中,Rg—— 高次曲线的基圆半径
Rs—— 展弦
可表示为Rs=B0+B1φ+B2φ2+B3φ3,B0,B1,B2,B3为待定系数,可由连续性条件确定。Rg与Rs两者之间存在如下的关系:
(3)
第3段基圆渐开线方程:
(4)
式中,φmax为型线的最大切向角。
1.2 型线的连续性条件
要使各段型线在连接点处能够光滑连接,需满足一定的连续性条件,为便于说明该连续条件,此处将型线方程表示为向量函数r(φ)的形式。
1) 点连续
第2段高次曲线r2(φ2)的末端与第3段基圆渐开线r3(φ3)的首端达到点连续,需满足:
r2(φ2)=r3(φ3)
(5)
2) 一阶可微
在连接点处斜率要相同,并且切矢方向相同。设α2和α3分别为型线r2(φ2)和r3(φ3)在连接点处切矢的模长,则两型线一阶可微的条件为:
(6)
3) 二阶可微
两涡旋型线r2(φ2)和r3(φ3)曲率相等,且法矢方向要一致,要满足如下条件:
(7)
同理,第1段基圆渐开线与第2段高次曲线在连接点处也需满足上述连续性条件。若满足上述条件中的前2个条件,则为一阶可微;若同时满足上述3个条件,则为二阶可微。
综合上述基线方程并对涡旋型线的齿头进行双圆弧修正后,运用法向等距法得到动、静涡旋的啮合图,如图2所示。
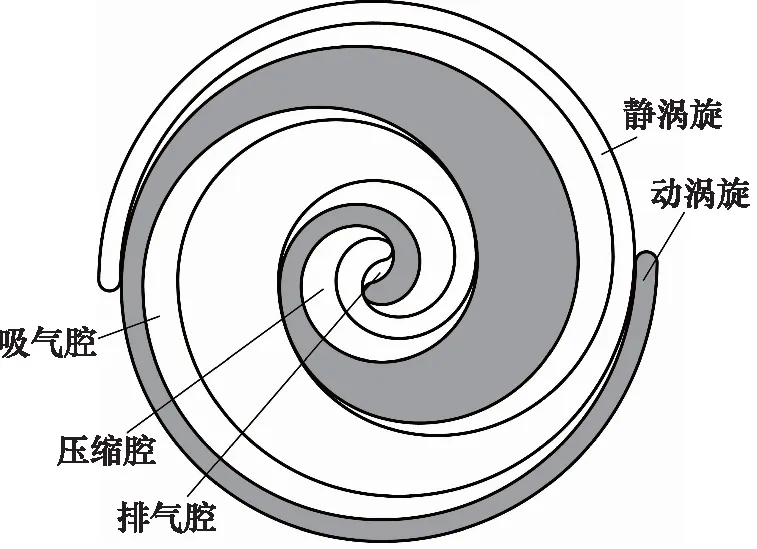
图2 动静涡旋的啮合
2 型线的容积性能
2.1 腔体容积计算
动、静涡旋啮合构成了一系列封闭的月牙形腔体,由外到内依次称为吸气腔(第一压缩腔)、压缩腔(第二压缩腔)和排气腔(第三压缩腔)。
1) 吸气腔容积
当主轴转角θ∈[0,φ2-φ1)时,吸气腔由第3段基圆渐开线和第2段高次曲线构成,此时腔体的容积为:
V11(θ)=2hRor[Rg(φ2)-a+L2+L3]
(8)
式中,Ror—— 回转半径
h—— 涡旋齿高
L2—— 第2段高次曲线对应基线的弧长
L3—— 第3段基圆渐开线对应基线的弧长
按下式进行计算:
(9)
(10)
当主轴转角θ∈[φ2-φ1,2π]时,吸气腔由2段基圆渐开线和1段高次曲线共同构成,此时其容积为:
V12(θ)=2hRor(L1+L2+L3)
(11)
其中:
(12)
(13)
(14)
式中,L1为第1段基圆渐开线对应基线的弧长。
综上所述,当θ∈[0,2π]时,吸气腔容积为:
V1(θ)=V11(θ)+V12(θ)
(15)
当主轴转角θ=0时压缩腔闭合,此时第一压缩腔容积V1(0)即为行程容积,该容积能够反映涡旋压缩机的压缩性能,对整机容积效率的影响较大。
2) 压缩腔容积
第1段基圆渐开线和第2段高次曲线构成了压缩腔,故第二压缩腔容积为:
V2(θ)=2hRor{L1+L2+[Rg(φ3-4π)-
Rg(φ3-2π)]}
(16)
其中:
(17)
(18)
3) 排气腔容积
如图3所示为双圆弧修正涡旋齿的示意图,图中φ为修正展角;∂为渐开线发生角;λ为修正圆弧中心角;Rd为修正大圆弧半径;Rx为修正小圆弧半径;γ为修正角。通过计算该涡旋齿,可得修正齿头的轴向投影面积为:
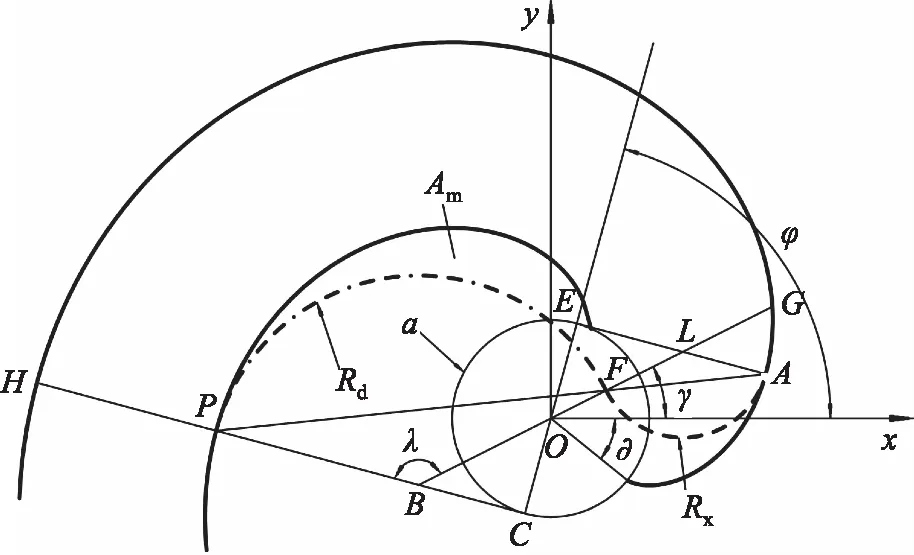
图3 双圆弧修正涡旋齿的示意图
(19)
θ*为开始排气角,大小为θ*=2π-γ。当θ>θ*时,第二压缩腔与排气腔连通,并合并为最大的中心排气腔,此时该腔体由第1段基圆渐开线和修正双圆弧构成,其腔体容积为:
(20)
2.2 压缩比
压缩比是衡量涡旋压缩机性能的一个重要指标,定义为:
(21)
式中,κ为绝热指数,通常取κ=1.3。
3 型线的动力学性能
涡旋压缩机在运行时,多个压缩腔会同时进行气体压缩,但由于压缩腔内的压力不同,会使气体对动、静涡旋产生气体作用力[16]。相对于静涡旋,作用于动涡旋上的气体力对涡旋压缩机的整机性能影响较大,因此本研究着重对作用在动涡旋上的气体力进行讨论。为便于分析计算,将气体作用力划分为轴向气体力、切向气体力和径向气体力3类。
3.1 轴向气体力
轴向气体力是沿主轴轴线方向作用在动涡旋上的力,该气体力会使动、静涡旋相互脱离,导致径向气体泄漏量增加,计算公式为:
(22)
式中,pi为第i个压缩腔的气体压力。
根据各压缩腔容积随主轴转角θ的变化规律,并假设压缩过程按绝热进行,则第i个压缩腔对应的气体压力为:
(23)
式中,p0为吸气压力,一般取p0=0.1013 MPa。
3.2 切向气体力
沿主轴切线方向作用在动涡旋上的气体作用力,称为切向力。该作用力会使动涡旋发生自转并产生倾覆力矩,其计算公式为:
(24)
式中,Lti为切向气体力作用线长度,具体可表示为:
(25)
(26)
(27)
3.3 径向气体力
径向气体力是沿动、静涡旋基圆中线方向作用在动涡旋上的气体力,该作用力会使动、静涡旋的径向间隙增大,导致切向气体的泄漏量加剧。计算公式为:
(28)
式中,Lri为径向气体力作用线长度,具体可表示为:
(29)
(30)
(31)
4 算例分析
以涡旋制冷压缩机为例,已知设计参数为:a=2.069 mm,h=35 mm,Ror=3 mm,连接点φ1=2.5 π,φ2=3.5 π,φ3=5.5 π。对涡旋型线的压力性能、容积性能和作用在动涡旋上的气体作用力进行数值模拟,结果如表1和图4~图8所示。
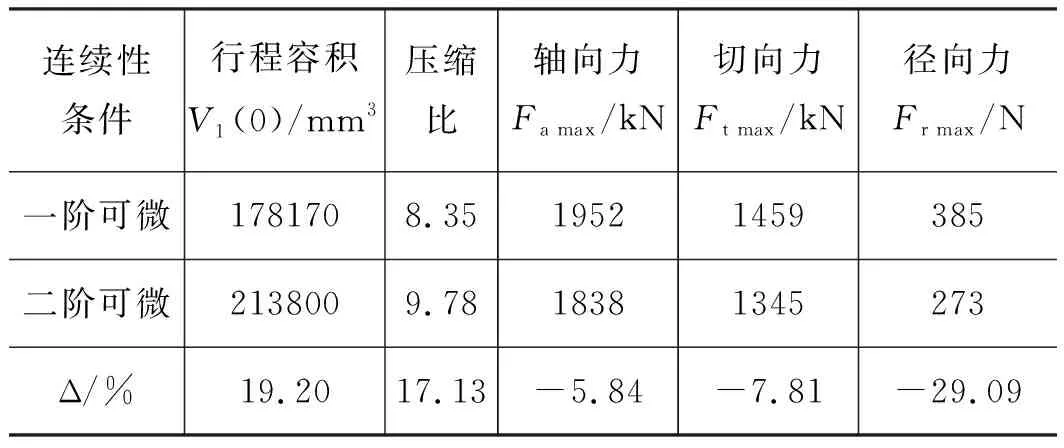
表1 不同连续条件下的型线性能
在由2条及以上曲线组合而成的变截面型线中,确保两曲线在连接点处能够光顺连接,是提升涡旋压缩机综合性能的关键。以往对组合型线在连接点处的研究,仅仅只是考虑将两曲线拼接,即只保证了2曲线在连接点处一阶可微,而并未将曲线的光顺性考虑在内,这样会使涡旋型线的性能降低,同时也不利于涡旋齿的加工。二阶可微能够使两曲线在连接点处的曲率相等,确保了曲线的光顺性。如表1中数据所示,是一阶可微和二阶可微条件下,得出的型线性能,可明显看出,二阶可微型线的各个性能均优于一阶可微型线的性能,即光顺的型线性能更好。
图4是根据涡旋型线的几何理论,模拟计算得出的不同连续条件下涡旋压缩机工作腔容积的变化规律。可以看出,虽然一阶可微和二阶可微型线的工作容积变化规律相似,但二阶可微型线的行程容积较大。与一阶可微型线相比,二阶可微型线的行程容积提高了19.20%,压缩比提高了17.13%。
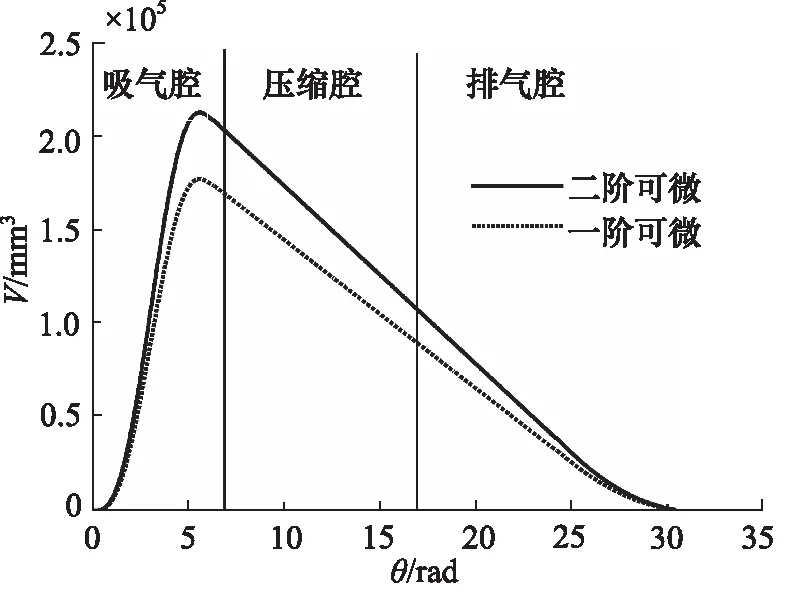
图4 工作腔容积变化规律
如图5所示,为涡旋压缩机压缩腔内气体压力的变化曲线图,当主轴转角θ在0~2π时,吸气腔尚未完全闭合,此时外界与吸气腔是相通的,工作腔内压力即为外界的气体压力;当θ≥2π时,工作腔内的气体开始被压缩,此时气体的压力值不断增大;当θ>θ*时,进入排气阶段,排气腔与外界相通,此时虽然腔体内的容积在不断减小,但气体压力值无变化,即为等压压缩。
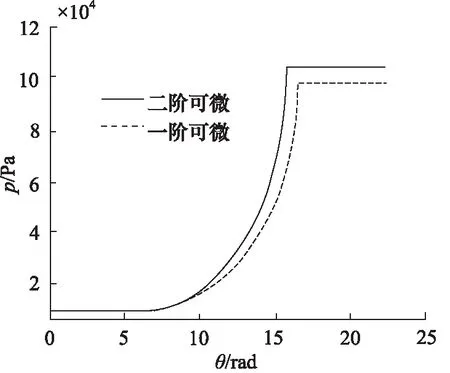
图5 气体压力变化曲线
图6~图8中,Fa1,Ft1和Fr1分别表示一阶可微条件下的轴向、切向和径向气体力,Fa2,Ft2和Fr2则分别表示二阶可微条件下的轴向、切向和径向气体力。
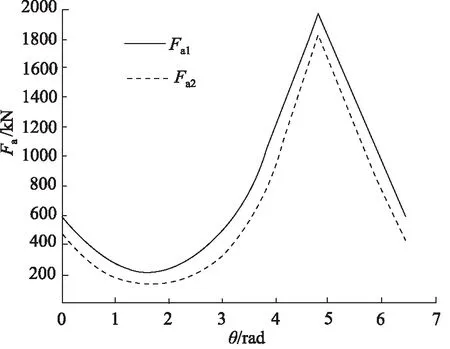
图6 轴向气体力
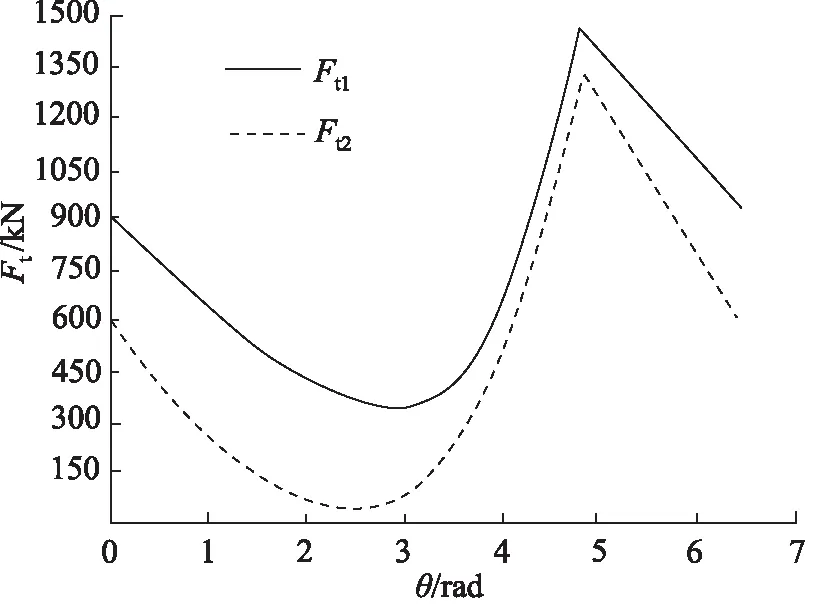
图7 切向气体力

图8 径向气体力
由图6和图7可知,轴向力Fa和切向力Ft都随着主轴转角θ的增大而先减小再增大最后变小,并且在二阶可微条件下受到的气体作用力均明显小于一阶可微条件下所受的力,而较小的气体力对于涡旋压缩机性能的提升是有益的。
由图8可知,径向气体力Fr的变化较复杂,二阶可微条件下所受的气体力较小,有利于减小切向气体的泄漏量。
5 结论
(1) 构建了二阶可微变截面涡旋型线,分析了封闭月牙形腔体的容积特性,并建立了涡旋型线的动力学随主轴转角的动态变化历程;
(2) 将二阶可微应用在组合型线设计中,不但解决了传统型线设计中只考虑将两段型线连接在一起而忽视型线光顺性的问题,而且也明显提升了涡旋型线的性能;
(3) 对涡旋型线的压力、容积性能和作用在动涡旋上的气体作用力进行了模拟分析,结果表明,与传统的一阶可微涡旋型线相比,二阶可微型线具有更大的压力、行程容积和压缩比,且3种气体作用力均明显较小,这为设计高效率和全性能要求的涡旋压缩机奠定了良好的基础,同时也为涡旋型线的设计提供了一种新的方法。
