罗茨转子轮廓的双对称图解构造法

李玉龙，秦运栋，张安民，赵 岩，李光宇

(宿迁学院 机电工程学院，江苏 宿迁 223800)

引言

罗茨泵的核心部件为2个完全相同的非接触转子，其旋转动力由同轴上另一对齿轮副提供[1]。由于转子轮廓是构成泵内多个容积单元的边界基础，因此其构造质量直接决定了如轻量化[2-3]、容积利用[4-5]、流场特性[6-7]、内泄漏[8]等的性能指标。目前，在充分降低径向泄漏和提高容积利用系数的轮廓方面，提出了以包络法和法线法为主的各种共轭轮廓构造方法[9]，以及由一对共轭段和若干过渡段组成的进一步提高形状系数的轮廓构造方法[2,10]。不过包络法需涉及2个转子轮廓间的共轭几何关系；法线法需涉及瞬径和瞬角的计算，其中将会涉及共轭轮廓曲线的二阶导数求解，甚至根本无法获得直接的函数表达式，这远非一般工程技术人员所能理解的[2]。另外在实物测绘后的轮廓构造中，由于不知道实物轮廓的具体曲线类型，所以必须全段测绘，而全段测绘中各分段误差又难以保证轮廓的构造精度[2,10]。有鉴于此，旨在将2个转子轮廓间的共轭关系，转化成单一转子轮廓上的双对称几何关系，以期实现便捷又高效地图解出待定分轮廓段的拟合曲线，并就此作进一步深入研究。

1 罗茨转子的半叶轮廓构造

罗茨转子的半叶轮廓如图1所示，由外同心圆弧段01、外过渡段12、外共轭段23、内共轭段34、内过渡段45、内同心圆弧段56共6部分首尾相连组成，相应的端点和连接点依序为位于(叶)顶(对称)轴O0上的顶点0、峰点1、外(共轭)起点2、位于中轴O3上的中节点3、内(共轭)起点4、根点5、位于(叶)谷(对称)轴O6上的谷点6，如图1所示。其中，转子上段12与配对转子上的峰点存在共轭关系，即段12为配对转子上的峰点在转子上的共轭轨迹线，转子上段45与配对转子上的内(共轭)起点存在共轭关系，即段45为配对转子上的内(共轭)起点在转子上的共轭轨迹线。

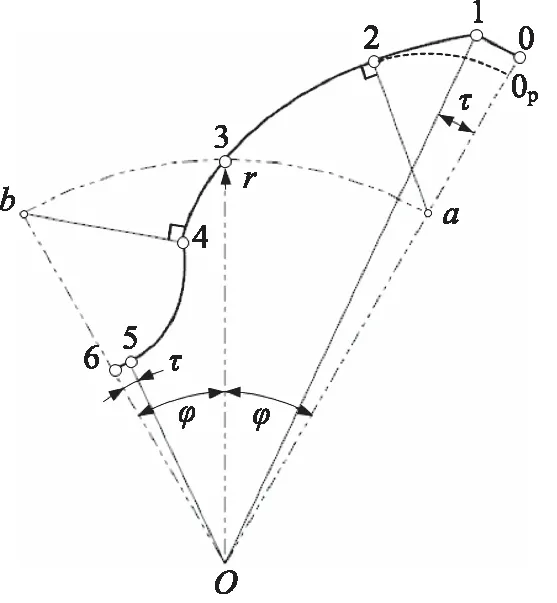
图1 罗茨转子的半叶轮廓构造

外同心圆弧段O1的设置，一方面因其等缝隙的密封方式能有效降低径向泄漏，另一方面也能充分缓解排气侧压缩反冲现象的影响[11]；O为转子中心，顶轴、中轴、谷轴及转子中心为确定半叶轮廓的端面轴系且由转子叶数N唯一确定，轴间角φ=π/(2N)，顶轴与节圆的交点为顶节点a，a2连线为外共轭段点2处法线，谷轴与节圆的交点为谷节点b，b4连线为内共轭段点4处法线。

以ε0表示共轭轮廓23的形状系数，即普通转子的形状系数，其值等于图1中O0p连线的长度除以节圆半径，设节圆半径为r，其中，0p2段为以a为圆心、a2为半径的圆弧；ε表示转子轮廓的形状系数，其值等于图1中O0连线的长度除以节圆半径；τ表示段01的圆弧角。则，段01为以O为圆心、εr为半径、τ为圆心角的圆弧；段56为以O为圆心、(2-ε)r为半径、τ为圆心角的圆弧。

研究表明，ε0越大和τ越小，ε及其容积利用系数就越大，容积效率就越高，且ε仅取决于ε0和τ的实际大小，与共轭轮廓的具体曲线类型及其连接形式无关[2,9-10]。其中，文献[12]给出了不同共轭曲线类型下ε0的不同上限取值及计算方法。

2 内外共轭段的双对称关系

2个完全相同罗茨转子在某一转角θ下共轭几何关系，如图2所示。其中，配对转子上各轮廓点及中心的标识以转子上对应标识后加“′”以示区别。设对应于转角θ的共轭点在转子、配对转子上的轮廓点分别为f，e′；c′e′为3′2′段的点e′处法线，且c′位于配对转子节圆上；fd为32段的点f处法线，且d位于转子节圆上。此时，c′和d重合且均为节点，c′e′的长度等于fd的长度设为ρ，c′e′与O′c′相交的锐角设为α。

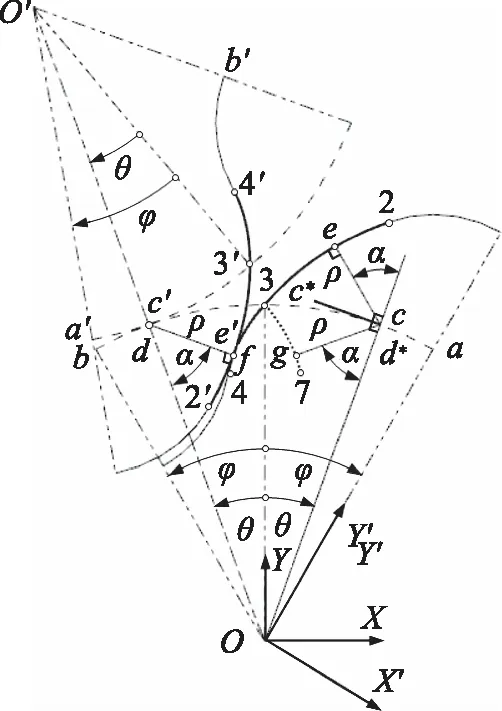
图2 共轭段间的双对称关系

由于转子与配对转子完全相同，则配对转子半叶轮廓上的c′e′，O′c′即转子半叶轮廓上ce，Oc，并作出点c处的节圆切线cc*。此时，ec与Oc相交的锐角等于α，ec的长度等于ρ。

在转子的半叶轮廓上，作出34，df段关于中轴O3对称的37，d*g段，此时d*与c重合，gc与Oc相交的锐角也等于α，gc的长度也等于ρ。

由ec与Oc相交的锐角等于gc与Oc相交的锐角，ec的长度等于gc的长度，得ec和gc关于cc*对称，即e和f间存在着“e↔cc*↔g↔O3↔f”的双对称几何关系，则：

(1)

式中，(xf，yf)和(xe，ye)为轮廓点f和轮廓点e在图2XOY坐标系下的坐标。

由给定的外共轭段23或内共轭段34，如果ρ(θ)，α(θ)一旦确定，那么待定的内共轭段34或外共轭段12由式(1)是极易构造的。但常见给定的共轭段多为图2中X′OY′坐标系下y′(x′)的函数表达形式，例如圆弧、椭圆弧、抛物线等，各自ρ(θ)，α(θ)的推导过程繁琐及结果表达复杂。如果在X′OY′坐标系下先依据已知共扼段的函数表达形式y′(x′)作出相应的轮廓曲线，然后利用双对称关系求出待定共轭段的轮廓曲线，则非常容易。

由于转子上外、内过渡段12，45分别为配对转子上的峰点、内(共轭)起点在转子上的共轭轨迹线，所以上述双对称关系同样适用于同一转子上过渡段12，45的求解。此时，已知的共扼段则变成为已知的峰点和内(共轭)起点。

3 双对称构造图解

3.1 待定共轭段

图2中，由给定共轭段的函数表达式及其ε0，在X′OY′坐标系中，作出共轭轮廓曲线。

如给定共轭段为外共轭段23。首先，在3a间的节圆弧上作出若干等分点c及在段23上的若干垂足点e和节圆切线cc*。其次，依据e→cc*→g→O3→f的双对称顺序得若干的点f。最后，由这若干的点f生成内共轭段34的拟合曲线。

如给定共轭段为内共轭段34。首先，作出内共轭段34关于中轴的对称曲线37，其次在3a间的节圆弧上作出若干等分点c及在37上的垂足点g和节圆切线cc*。其次，由这若干垂足点g关于各自对应的cc*对称后得若干对称点e。最后，由这若干对称点e生成外共轭段23的拟合曲线。

3.2 待定外过渡段

无论给定段为外共轭段还是内共轭段，通过前述待定共轭段的双对称构造后，内起点4及其关于中轴的对称点7的位置是已知的。

首先，在图3中ap间的节圆弧上作出若干等分点i及其节圆切线ii′，和中轴对称点7关于ii′对称后的若干对称点j。

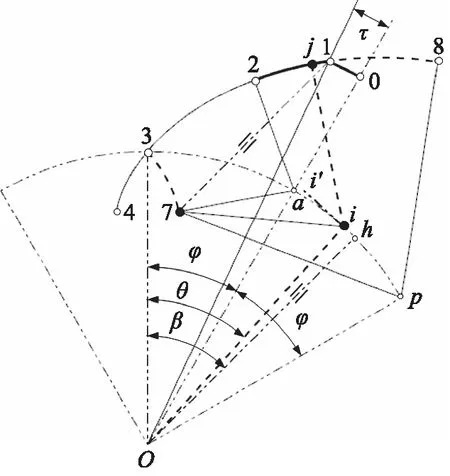
图3 内起点和外过渡段间的双对称关系

其次，由此若干的点j生成外过渡段28的拟合曲线，其与圆心角为τ的半径线O1的交点即为峰点1，并由此量测出O0的长度和计算出相应的形状系数ε，及截取出对应于圆心角为τ的外过渡段21的拟合曲线。

最后，作出过O且和71连线平行的直线段Oh，由其与节圆的交点得峰节点h和量测出峰点避让角β，该值在文献[2,10]中是由数值方法计算得到的。

3.3 待定内过渡段

在前述峰节点h确定后，设O1连线与节圆的交点为k。首先，在kh间的节圆弧上作出若干等分点m及其节圆切线mm′。其次，作出峰点1关于mm′对称后的若干点n。最后，由这若干的点n生成拟合曲线79，并由中轴对称出内过渡轮廓段45，如图4所示。

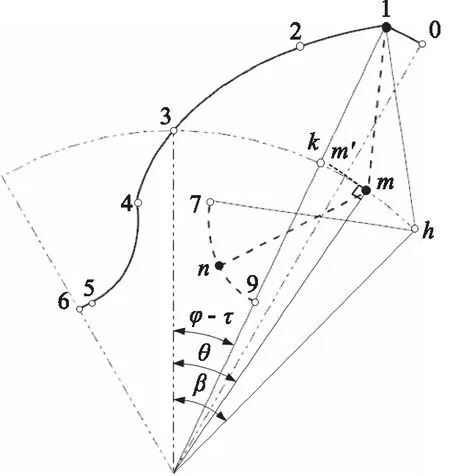
图4 峰点和内过渡段间的双对称关系

4 抛物线外共轭段双对称例

取外共轭段为N=3，φ=π/6，r=100 mm，τ=3°，ε0=1.3865下的抛物线：

(2)

其中，ρ(θ)，α(θ)难于求解[2]。

第一步，在图5X′OY′的坐标系下，先由式(2)作出该抛物线的规律曲线t3，并截取出对应于圆心角为3°的外共轭段23。后取5等分点c，由前述的双对称构造法，得内共扼段34的拟合曲线，且与其规律曲线[2]非常一致。事实上，抛物线为二次曲线，6点的拟合精度已非常高。

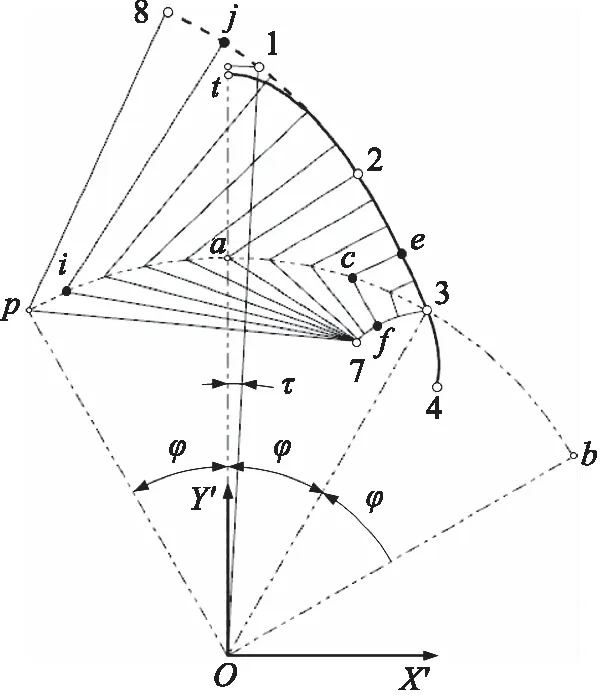
图5 抛物线例的峰点和外过渡轮廓段确定

第二步，图5中先取5等分点i，由前述待定外过渡段的双对称构造法，得峰点1、峰节点h及截取出外过渡轮廓段12拟合曲线段；然后测量和计算出ε=1.4807，β=49.71°，与数值方法的计算值完全相同[2]，如图6所示。

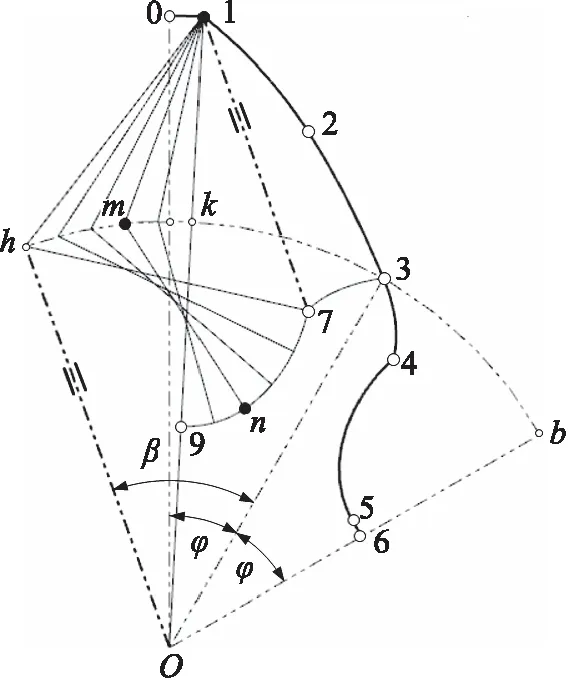
图6 抛物线例的峰节点和内过渡轮廓段确定

第三步，图6中取5等分点j，由前述待定内过渡段的双对称构造法，得内过渡段45的拟合曲线，与其对应的规律曲线非常一致[2]。

5 转子副共轭区多密封点位

当转子副以图7a所示为起始位置的旋转过程中，各分轮廓段均全程共轭参与，为此当旋转角在[0，τ)内时有5个，在旋转角为τ时有4个，在(τ，β-φ)内时有3个，如图7b所示，在旋转角为(β-φ)时有2个，在(β-φ，φ)内有1个密封点位。其中，图7a所示为转子谷轴与配对转子顶轴重合时的起始位置，图7b所示为由起始位置按转子逆时针、配对转子顺时针方向旋转10°后的位置。

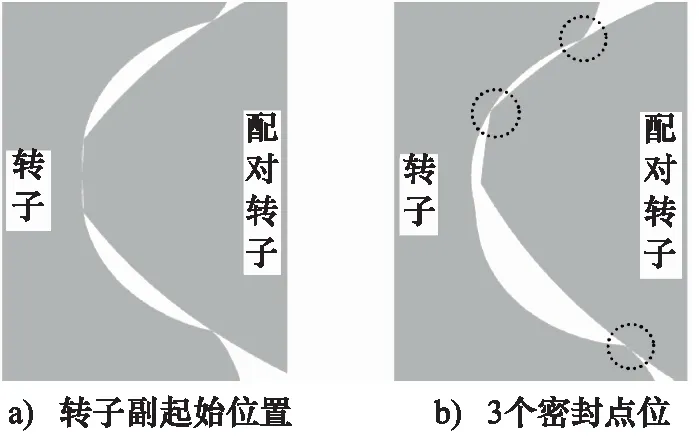
图7 转子副共轭区内的多密封点位

相对于全程仅有1个密封点位的普通转子[1]，多点位密封区间比为β/φ-1=65.7%，为此将取得更小的共轭泄漏，加上2τ径向等缝隙密封，内泄漏更小，容积效率更高。

由于非高速气体介质和非接触间隙的存在，所以共轭区多密封点位不会形成像齿轮泵那样的困油现象。

6 结论

(1) 罗茨泵/风机用转子的半叶轮廓由外同心圆弧、外过渡、外共轭、内共轭、内过渡、内同心圆弧共6段，首尾相连构成；

(2) 转子全轮廓关于中轴和节圆切线的双对称关系，实现了所有待定分轮廓段便捷又高效的拟合图解，拟合精度高，图解质量好；

(3) 转子全轮廓段的共轭参与将形成2～5个多密封点位和案例65.7%的密封区间，共轭泄漏更少，加上转子顶部的等缝隙密封构造，径向泄漏更小，容积效率更高。