不同气室充气容积对油气弹簧动态特性影响分析

刘同昊，石运序，曹常贞，戚积财，王兴旺，贾炎冰

(1.烟台大学 机电汽车工程学院，山东 烟台 264005；2.烟台未来自动装备有限责任公司，山东 烟台 264001)

引言

油气弹簧是油气悬架的核心部件，以气体(一般是氮气)作为弹性元件，在气体与活塞之间引入油液作为传力介质[1-2]。与传统减震器相比，具有良好的非线性输出特点，大大提高了车体的平顺性，所以广泛应用于矿用自卸车等非公路车辆悬架中。油气悬架一直是国内外学者研究的重点，王增全等[3]建立了连通式油气悬架数学模型，研究了参数变化对连通式油气悬架刚度与阻尼特性的影响。关晋凯等[4]根据某自卸车前悬油气缸的结构及工作原理，搭建了AMESim仿真模型，分析了影响悬挂缸输出特性的因素。刘文彦等[5]对油气悬挂输出特性进行了理论、模拟、实验三者的结果对比分析，针对模型参数进行了修正。袁加奇等[6]研究了油气弹簧不同工作状态下结构参数变化对油气弹簧输出力特性的影响，提高了车辆行驶的安全性和舒适性。

本研究以某公司设计的油气弹簧为研究对象，建立其输出特性数学模型，利用AMESim搭建了悬挂缸动态仿真模型，详细分析了悬挂缸输出特性曲线，研究了工作参数对动载压力随行程变化的影响和悬挂缸缓冲原理，为后续提高油气弹簧的使用寿命、数字化设计等提供了分析方法和理论依据。

1 单气室油气弹簧数学模型的建立

1.1油气弹簧力学模型分析

以矿用宽体车前悬油气悬挂缸为研究对象，在满载静平衡状态下对悬挂缸进行受力分析[7-8]。假定油液不可压缩，缸内气体与油液不互溶，建立单气室油气混合式悬挂缸的受力模型如图1所示。

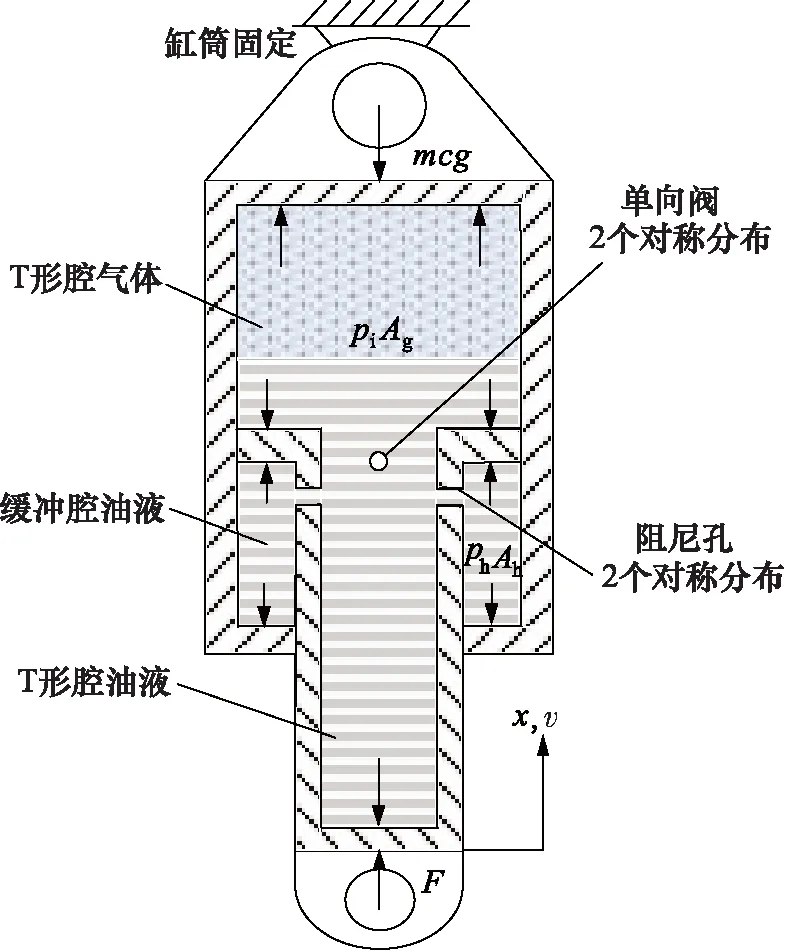
图1 油气弹簧受力简图

实际安装中油缸倒置，气室位于T形腔上层。设压缩方向为正方向，拉伸方向为负方向，当达到平衡状态时，缸体受到来自车身的重力，活塞杆受到来自车架的支撑力，其值等于悬挂负载。T形腔受到轴向的气体和液体压力；缓冲腔受到液压力。在静平衡状态下，无杆腔与环形腔压力相等。

忽略缸筒与活塞间的摩擦，对杆进行受力分析，得活塞杆输出力公式为：

FH=piAg-phAh

=pi(Ag-Ah)+(pi-ph)Ah

=Fe+Fd

(1)

式中,FH—— 活塞杆输出力

pi—— 气体工作压力

ph—— 缓冲腔油压

Ag—— 悬挂缸大腔有效面积

Ah—— 悬挂缸小腔有效面积

由式(1)可知：

(2)

式中，Fe—— 气体弹性力

Fd—— 油液阻尼力

Δp—— 两腔压差

1.2 弹性力数学模型建立

气体弹性力是指缸内气体被压缩时所产生的作用力。以油气弹簧压缩起点为初始状态，当活塞相对缸筒压缩时，此过程T形腔容积逐渐减小，缓冲腔容积逐渐增大。油液一方面经阻尼孔和单向阀流入缓冲腔；另一方面用来补充T形腔内被压缩的气体体积[9]。将腔内气体看做理想气体，得气体体积变化公式为：

Vi=V0-(Ag-Ah)·x

(3)

式中，Vi—— 气体瞬时体积

V0—— 初始充气体积

x—— 活塞杆与缸筒的相对位移

根据式(2)、式(3)，结合理想气体状态方程:

(4)

式中，p0为初始充气压力。

整理得油气弹簧弹性力公式为：

(5)

式中，r为气体多变指数。

1.3 阻尼力数学模型建立

阻尼力是指油液流经阻尼孔或单向阀时，因节流作用而产生的阻力。由油气弹簧节流孔尺寸，可知均属厚壁孔口，根据小孔流量方程[10-11]，流经阻尼孔和单向阀的流量方程可表示为：

(6)

式中,Cq—— 孔口流量系数

A—— 孔口节流面积

ρ—— 油液密度

油气弹簧物理结构如图2所示。

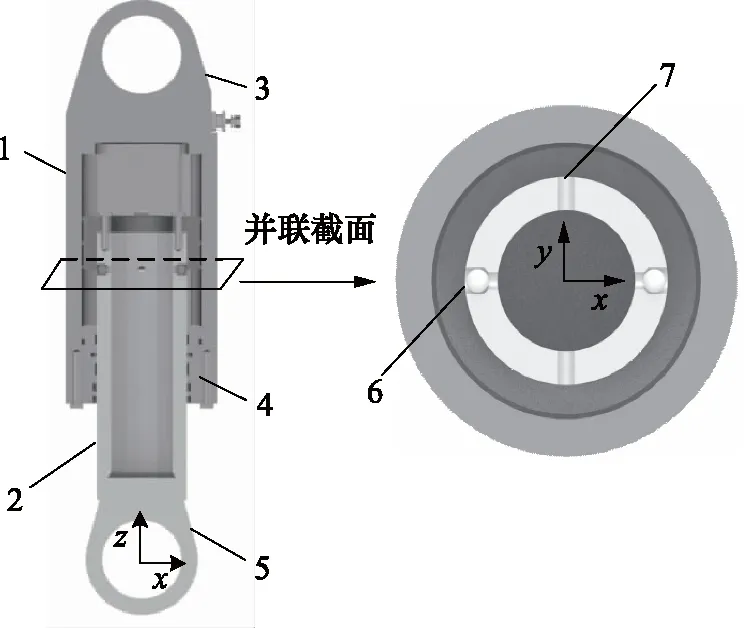
1.缸筒 2.活塞杆 3.上支耳 4.前盖5.下支耳 6.单向阀 7.阻尼孔图2 油气弹簧结构简图

由图2可知阻尼孔和单向阀均在同一水平面内且对称分布，属并联结构，因此二者孔口两端压差相等，即Δpo=Δpv。由于油气弹簧工作过程中，单向阀只在压缩行程时打开，在此引入符号函数sign，则腔内油液流量可表示为：

(7)

式中，Cd—— 节流孔流量系数

Cv—— 单向阀流量系数

Ad—— 阻尼孔过流面积

Av—— 单向阀过流面积

根据相关理论，单位时间里缓冲腔内增加或减少的流量等于流进或流出阻尼孔和单向阀的流量，则流经阻尼孔或单向阀的流量又可表示为：

Q=Ah·vr

(8)

式中,Ah—— 缓冲腔横截面积

vr—— 活塞与缸筒的相对运动速度

由式(7)、式(8)得两腔之间的压力差为：

(9)

联立式(2)、式(9)得阻尼力公式为：

(10)

式中，sign为符号函数；取油气弹簧压缩行程为正方向。在压缩行程中，速度v≥0，sign=1; 在拉伸行程中，速度v≤0，sign=-1。

2 仿真模型的建立

2.1 油气弹簧动态仿真模型建立

根据油气弹簧结构和工作原理，利用AMESim搭建如图3所示动态仿真模型。

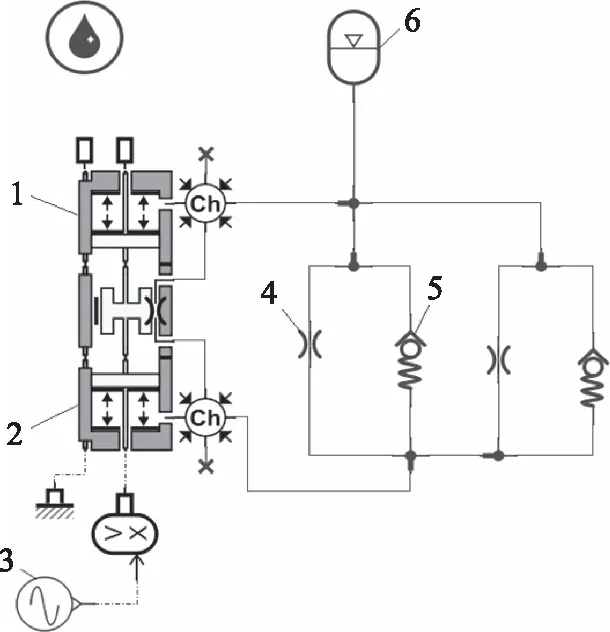
图3 油气弹簧动态仿真模型

将元件1活塞杆参数设为0，模拟图1中T形腔，元件2活塞杆直径设为120 mm，模拟缓冲腔，通过元件3输入频率和幅值等激励信号，模拟路况，元件4，5并联，分别模拟节流孔和单向阀，元件6模拟油气弹簧内气体，模型主要参数如表1所示。

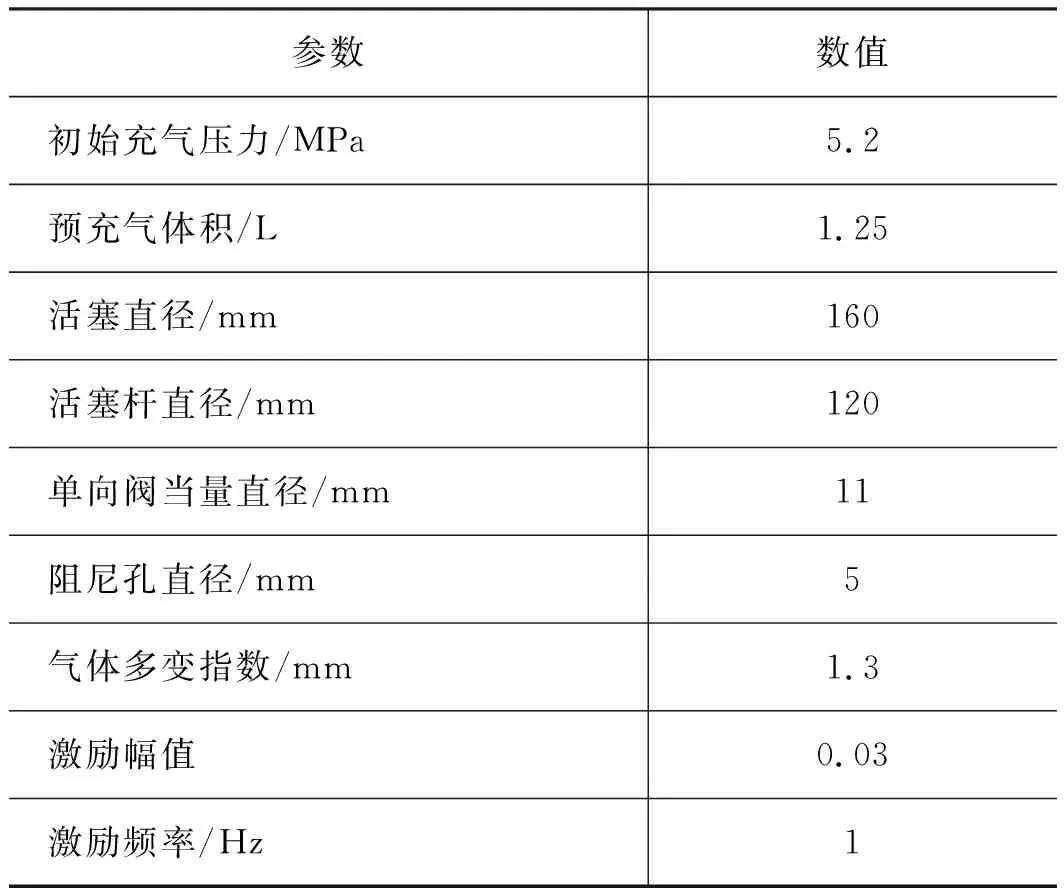
表1 主要参数设置

2.2 数学模型求解模块搭建

根据前面所建立的悬挂缸输出力数学模型，利用AMESim/信号库搭建如图4所示公式模型，对数学模型进行仿真求解。

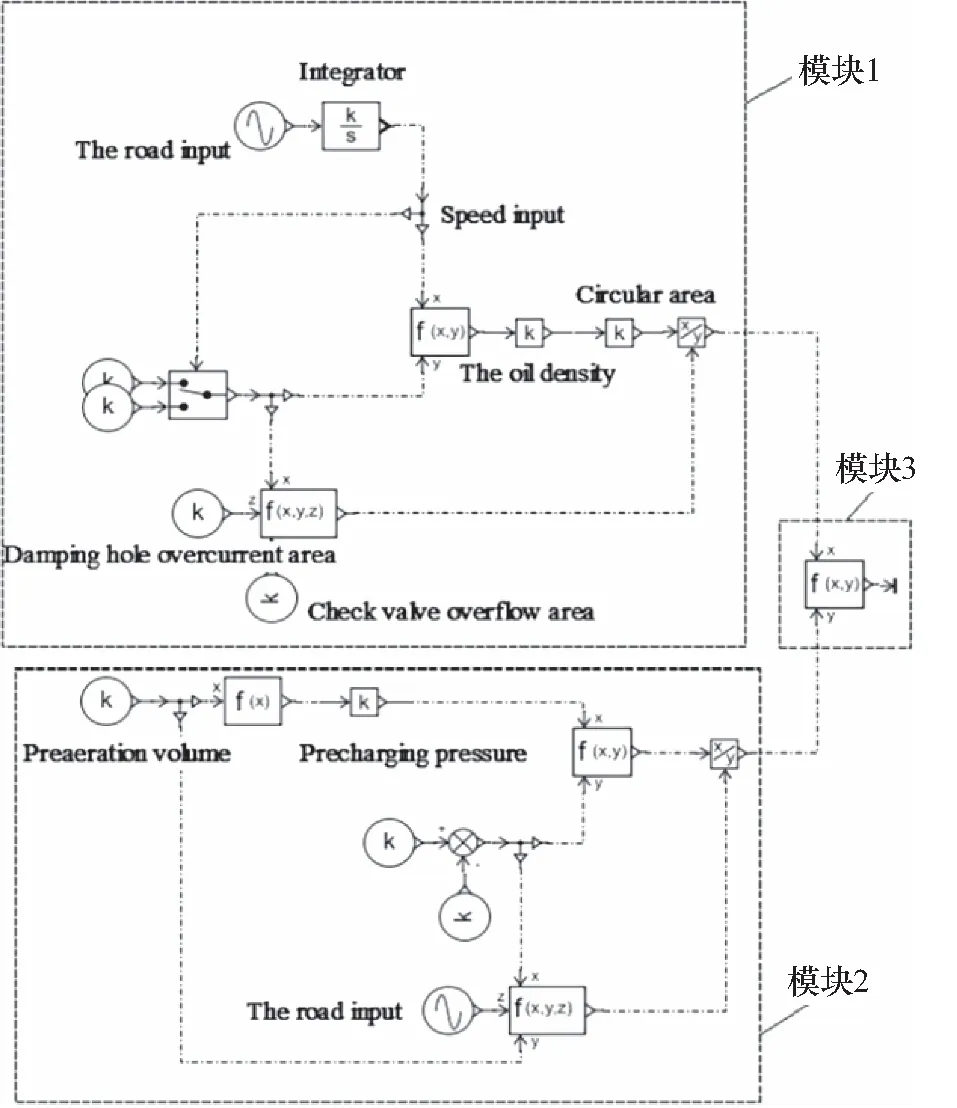
图4 油气弹簧公式求解模型

模块1为阻尼力理论求解模型，模块2为弹性力理论求解模型，模块3为悬挂缸输出力。

3 仿真结果分析

3.1 动态特性实验与仿真对比分析

实验初始条件与仿真模型一致，在动态仿真模型中输入幅值为0.03，频率为1 Hz的激励信号，将仿真时间设为1 s，仿真步长设为0.001 s。经后处理得如图5所示弹性力随时间变化对比曲线和图6所示阻尼力随时间变化对比曲线。

从图5可见，理论和仿真结果与实验数据基本吻合，弹性力随时间呈非线性变化趋势。0～0.5 s时，油气弹簧处于压缩行程，0.5～1 s时，处于拉伸行程。在压缩行程中，气体不断被油液挤压，体积逐渐减小，气体压力不断增加，而压力作用面积不变，因此弹性力随时间的推移迅速增大，当达到平衡位置时，弹性力最大为87 kN。在伸张行程中，活塞杆向外伸出，腔内容积增大，气体膨胀体积增大，压力不断变小，因此弹性力逐渐减小。当达到平衡位置时，弹性力最小为59 kN。综上可知，气体弹性力主要表现在压缩行程中，因此车辆在复杂路况行驶时，油气弹簧可以很好的缓解外部冲击，改善车辆行驶时的平顺性。

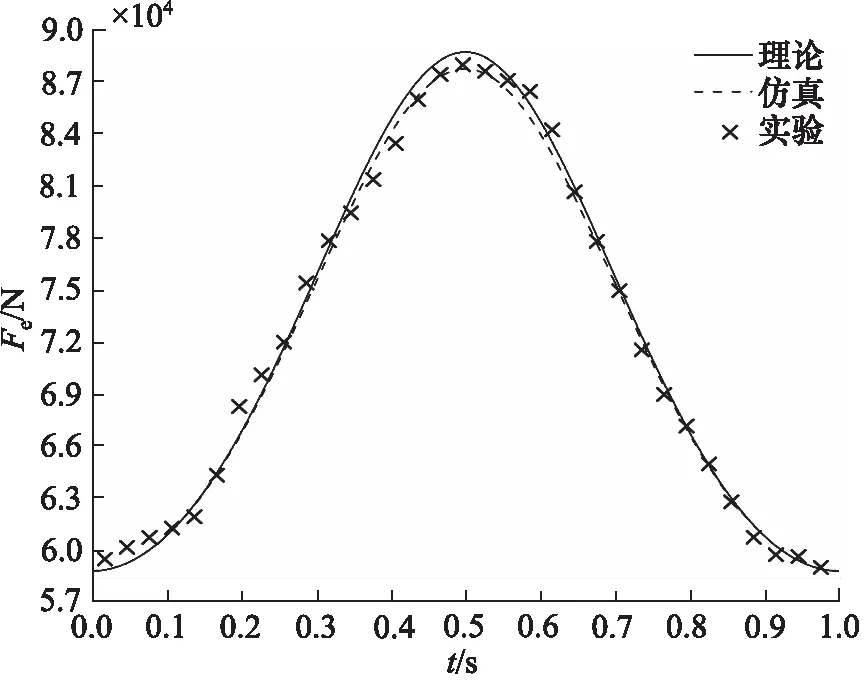
图5 弹性力随时间变化曲线

由图6可知，理论和模拟结果与实验趋于一致，阻尼力随时间呈非线性变化趋势。在0～0.5 s即压缩行程时，阻尼力较小且变化缓慢。由式(10)可知，压缩时T形腔油压大于缓冲腔油压，单向阀打开，油液通过阻尼孔和单向阀流入缓冲腔，当达到平衡位置的瞬时，两腔压差为0 MPa，阻尼力归为0 N。在0.5～1 s 即拉伸行程时，阻尼力较大且变化较快。T形腔油压小于缓冲腔油压，单向阀关闭，油液仅通过阻尼孔流入T形腔。因单向阀只在压缩行程打开，在拉伸行程中流过阻尼孔的流量要大于压缩行程，相应地拉伸流速也大于压缩流速，所以拉伸时阻尼力要明显大于压缩时阻尼力。综上可知，阻尼特性主要表现在拉伸行程中，当车辆在复杂路况行驶时，油气弹簧可以有效的衰减振动，防止活塞与缸筒底部发生相对碰撞，提高驾驶舒适性。

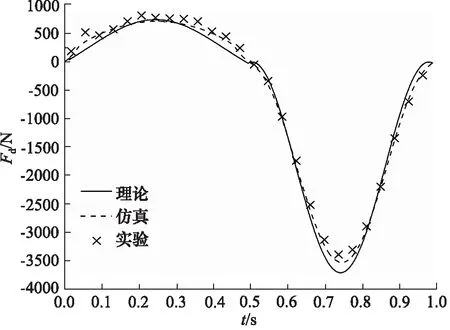
图6 阻尼力随时间变化曲线

由图7可知，理论、仿真和实验数据基本吻合，悬挂缸输出力随位移呈非线性变化，这主要是由气体弹性力和孔口出流所产生的阻尼力等非线性因素造成的。设位移为0 mm时为压缩起点，在一个往复运动的过程中，活塞杆首先相对缸筒向内压缩，压缩过程中，输出力呈非线性增大趋势，当到达平衡位置时，输出力达到最大值87 kN。在拉伸过程中，输出力呈非线性减小趋势，最后回到压缩起点，此时输出力最小为59 kN。结合图5和图6，由式(1)可知，由于拉伸过程阻尼力为负值，所以压缩过程的输出力要大于拉伸过程。因此形成了一个扁球形状的闭合面积，此面积则代表一个往复运动周期内悬挂缸所消耗的振动能量。

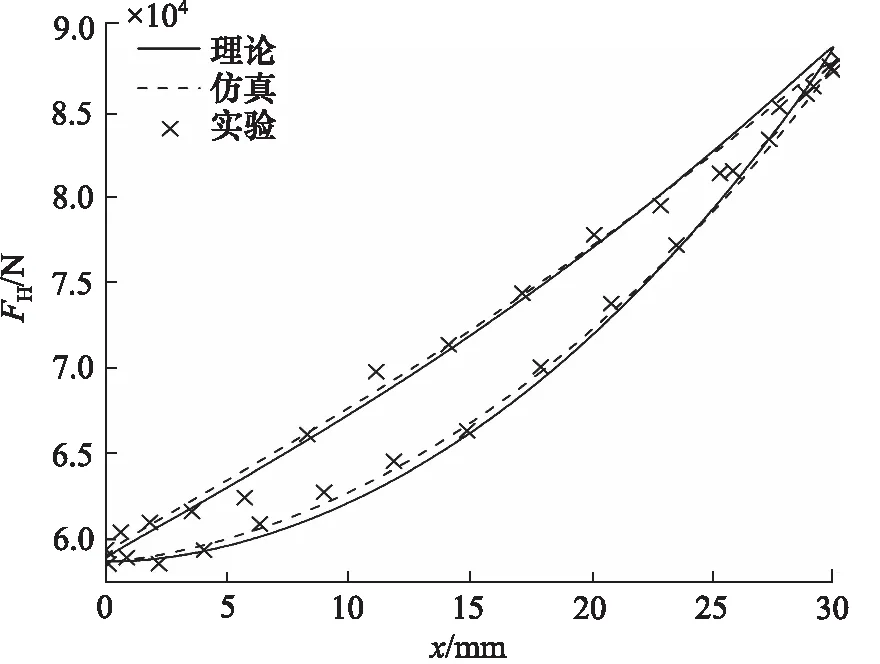
图7 输出力随位移变化曲线

综上可知，弹性力在压缩行程得到充分发挥,系统消耗振动能量较少，在拉伸行程阻尼力起主导作用，消耗振动能量较多。

3.2 不同预充气体积下行程长度对比分析

保持其他参数不变，取3种不同数值的初始充气体积分别为1.05, 1.25, 1.45 L，利用AMESim批处理功能，得悬挂缸动载压力随行程的变化曲线，如图8所示。

图8中实线为仿真模拟，虚线为理论计算。可见动载压力随行程呈非线性增大趋势，预充气体积越小，随行程变化时曲线的斜率越大，对应的动载压力也越大。以额定动载压力15.6 MPa为基准，由图8可知当初始充气体积为1.05 L时，对应理论行程为53 mm，仿真行程为57 mm；当初始充气体积为1.25 L时，对应理论行程为63 mm，仿真行程为67 mm；当初始充气体积为1.45 L时，对应理论行程为73 mm，仿真行程为77 mm。可见理论计算所得行程略低于仿真模拟所得行程，这是因为在建立数学模型时，将油液视为不可压缩，而利用AMESim软件建模仿真时，是考虑了油液压缩性的，所以仿真时，行程长度需要略大于理论行程，进一步压缩气体，才能使腔内达到与之相同的压力。以仿真数据为准，可知预充气体积越大，到达额定动载压力时的行程长度越大。

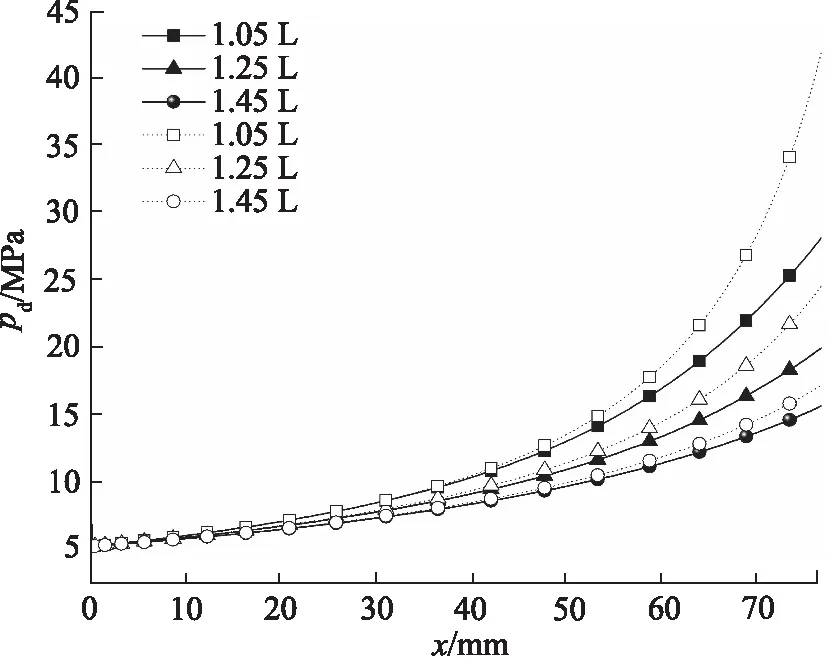
图8 不同充气体积下行程对比分析

通过以上分析得到当预充气体积为1.25 L，预充气压力为5.2 MPa时，行程长度不宜超过67 mm。

3.3 油气弹簧缓冲机理分析

采用正弦激励信号来模拟颠簸的路面，通过输入不同的激励幅值，来模拟研究油气弹簧在不同路面起伏下进行缓冲的原理。由3.1节可知，油气弹簧中主要由气室起到缓冲作用，相当于弹簧，因此主要分析弹性力及刚度特性来对缓冲原理进行研究[9]。对式(5)进行位移求导得刚度公式为：

(11)

取不同初始充气体积分别为1.15,1.25,1.35 L，得如图9所示刚度特性曲线。

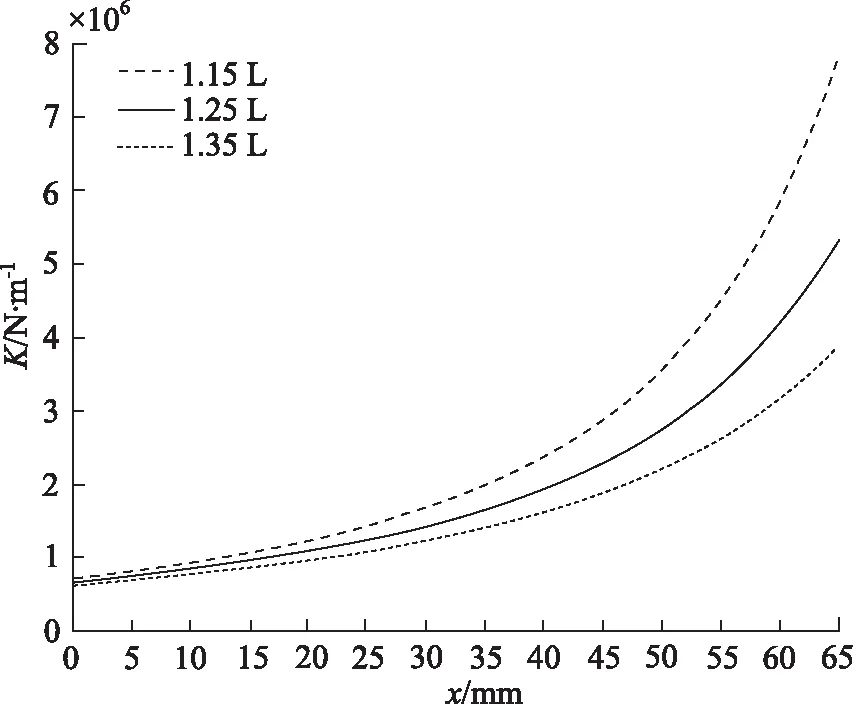
图9 刚度特性曲线

由图9可知，刚度随行程呈非线性增大趋势。当行程不变时，初始气室充气体积越大，刚度越小。

图10为不同路况下，达到压缩终点平衡位置时输出力与初始气室充气容积关系曲线。

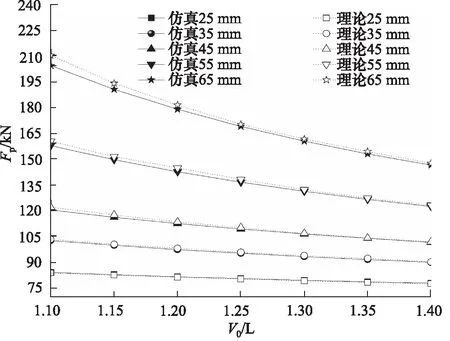
图10 平衡点输出力随初始气室容积变化曲线

图10中，实线为仿真数据，虚线为理论计算。可知，当路面起伏程度即悬架行程不变时，到达压缩终点平衡位置时的输出力随气室充气容积的增大而减小，且路面起伏越大，变化越明显。当初始气室充气容积恒定，平衡点输出力随路面起伏程度的增大而增大。

由图7可得，压缩终点平衡位置时的输出力等于最大弹性力。结合图9和图10，对悬挂系统缓冲机理进行分析，当车辆在起伏程度较小的路面行驶时，悬架行程较短，到达平衡位置时活塞杆输出力，即气体弹性力较小，因此油气弹簧在短行程内的刚度变化较小，此过程悬架较“硬”，有利于车辆操作的稳定性[12]。当车辆在起伏程度较大的路面行驶时，悬架行程较长，到达平衡位置时活塞杆输出力，即气体弹性力迅速增大，因此油气弹簧在长行程内的刚度变化较大，此过程悬架较“软”，有利于驾驶员乘坐的舒适性。

综上可知，可以通过改变气室初始容积来设置单气室油气悬架行程中的弹性力及刚度，使油气弹簧刚度控制在合适范围。从而使车辆在不同路况行驶时，既能保证乘坐舒适，又能保证操作稳定。

4 结论

本研究建立了悬挂缸输出力数学模型，利用AMESim软件搭建了某型号油气弹簧仿真模型，将仿真结果与实验数据对比，深入分析了输出力-位移特性曲线，研究了悬挂系统缓冲机理及工作参数对动载压力随行程变化的影响规律。结果表明：

(1) 悬挂缸输出力主要由气体弹性力和油液阻尼力共同决定;

(2) 当预充气体积为1.25 L，预充气压力为5.2 MPa时，行程长度不宜超过67 mm;

(3) 初始气室充气容积对悬挂系统缓冲性能影响较大，当悬挂行程小于35 mm时，悬架较“硬”，有利于操作稳定性，当悬挂行程大于35 mm时，悬架较“软”，保证了乘坐舒适性。由此可知，可以通过改变气室容积来设定到达额定动载压力时的行程长度和刚度范围，使油气弹簧在不同路况下，能在满足额定行程的范围内正常工作，对延长其使用寿命具有重要意义。