可变阻力特征对锥套拖曳位置的影响
2021-09-16张维峰薛长宝刘学强
徐 阳,张维峰,薛长宝,刘学强
(1.南京航空航天大学航空学院,南京 210016;2.中国航空工业集团有限公司南京机电液压工程研究中心,南京 211106;3.中国航空工业集团有限公司西安飞机工业(集团)有限责任公司,西安 710089)
空中加油技术在现阶段的航空领域具有重要的战略价值,其中软管⁃锥套式(简称软式)空中加油技术因其设备结构简单、易于拆装,且对加油机要求不高,为世界各国广泛采用。加油锥套是软式加油装置核心组件之一,安装在加油软管末端,能够增大受油接头的对接范围,其上安装的稳定伞可以提供阻力,使锥套在大气湍流、加油机尾涡和受油机头波等多重因素影响下保持相对稳定。目前,传统结构的稳定伞分为高速伞和低速伞。给低速飞行器,例如直升机加油时,加油机的飞行速度要在67 m/s 左右;给高速飞行器,例如喷气式飞机加油则需要180 m/s[1]。这种加油环境的不匹配要求加油机在附近的基地降落,在低速和高速加油设备之间更换,通常消耗至少30 min[2]。定义稳定伞的阻力特征为阻力系数Cd与参考面积S的乘积。由于传统稳定伞阻力特征恒定,加油包线较小,无法实现一伞通用,因此业内提出了可变阻力特征稳定伞的概念。可变阻力特征稳定伞就是通过一定的控制手段,在飞行速度和高度发生变化时调整稳定伞的结构,使阻力特征发生变化,控制锥套位移变化量在较小范围内,可以同时适用于高速和低速加油,极大地扩展传统加油设备的加油包线。
加油装置总阻力的75%以上是由稳定伞伞衣提供的[3],因此调整伞衣的迎风面积可以有效地改变整体结构的阻力,从而控制加油锥套的下沉量。目前可变阻力特征稳定伞有3 种思路[4]:(1)双层伞衣,需要较大阻力时打开两个伞衣,需要较小阻力时只打开主伞。(2)变伞撑角,通过机构控制伞撑角的变化,以此来控制伞衣的迎风面积。(3)弹性结构,通过弹性结构的变形改变稳定伞的迎风面积,实现阻力的自适应控制。目前多数设计都采用变伞撑角方案,文献[5⁃7]对传统稳定伞加装了不同的控制机构来改变伞撑角,从而控制伞衣的迎风面积。
加油机飞行速度和高度发生变化时加油锥套阻力特征与拖拽位置的关系如图1 所示。为确保对接过程中飞机安全,软式空中加油一般要求锥套下沉量在1.5~5 m 范围内(图中蓝色虚线范围)。当来流速度增大时,锥套整体下沉量减小,曲线向下移;当海拔升高时,锥套下沉量增大,曲线向上移。从图中可以看出阻力特征恒定时可覆盖的速度域和高度域都很小,如图中红色直线1 所示,阻力特征固定为0.3 时,覆盖的速度域为马赫数0.5以上,高度域为6 000 m 以下;当阻力特征从0.3 变化到0.8 时,如直线2 所示,速度域可以拓宽至马赫数0.35,高度可以拓宽至10 000 m。阻力特征变化范围越大,可覆盖的速度域和高度域范围就越广。因此,改变稳定伞的阻力特征可以显著地扩展加油包线。

图1 稳定伞阻力特征与下沉量关系图Fig.1 Relationship between drag characteristic and paradrogue draught position
1 变阻力特征稳定伞模型
目前各国使用的稳定伞结构基本相同,由两部分构成:支架和伞衣。支架由金属材料制成,起到支撑和传递载荷作用。伞衣成锥环装,由柔性织物制成,有的伞衣上会有开孔或缝隙,用来提高稳定性和减小阻力。Kapseong 等[3]通过全因子实验分析,给出了支架迎角、稳定伞伞面面积以及伞面开孔等因素对于锥套稳定伞整体阻力的影响。支架数量对于整体的阻力也有影响,在不加装伞衣的情况下,支架数量越多,稳定伞阻力越大;加装伞衣后,增加支架数量会导致伞衣的有效面积减小,整体阻力减小[8]。本文采用文献[6]中的变伞撑角稳定伞模型,如图2 所示。该模型通过弹簧的收缩来调节伞撑角从而实现阻力的控制。支架部分变伞撑角原理如图3 所示:当软管在空中的拖曳形状与锥套的下沉位置保持稳定时,称这种情况为平衡状态,平衡状态下伞面传递给支架的载荷与弹簧变形产生的拉力达到平衡,稳定伞保持结构不变;当加油机速度增大或者来流空气密度增大,稳定伞表面的气动载荷也增大,平衡状态被破坏,伞面传递给支架的载荷增大,迫使支架“并拢”,弹簧形变量增大,伞衣减小的迎风面积抵消了一部分增大的气动载荷,最终与弹簧产生的拉力相平衡,重新恢复平衡状态;反之亦然,当外部工况变化导致稳定伞产生的载荷减小时,弹簧产生的拉力拉动杠杆臂向内转动,支架“张开”,伞撑角变大,伞衣迎风面积增大,补偿了一部分减小的阻力,当气动阻力与弹簧拉力相平衡时,系统恢复到平衡状态。

图2 稳定伞模型Fig.2 Paradrogue model
稳定伞伞面形状的确定采用文献[9]中的方法,将伞面轮廓离散为微段,在来流速度V∞下求解离散轮廓运动方程直至收敛稳定。计算时将伞衣当作不可变形面,简化后不同伞撑角的锥套模型如图4 所示。

图4 不同伞撑角下稳定伞模型Fig.4 Paradrogue model at different struct-arm separation angles
2 软管数学模型
2.1 软管形状建模
经典的柔性体系统理论中,理想的绳索是一种不抗压、不抗弯、不抗扭、只受拉的结构元素,加油软管作为一种类绳索橡胶管,横截面由内衬层、埋线层和外衬层组成[10],当加油过程正常时,软管的受力模型很大程度与理想绳索相同,但相比柔性绳索加油软管具有一定的承压、抗弯和抗扭能力。绳索系统常见的建模方式有两种,一种是偏微分方程形式的连续体模型,另一种是常微分形式的有限段离散模型[11]。相比第一种方式,第二种方法更为直观、便捷,并且可以保证良好的精度。本文使用常微分形式的有限段离散模型对软管进行建模,采用球棍模型,如图5 所示,将软管离散为一段段由光滑球铰链接的刚杆,刚杆质量集中在球铰上。为方便表示,对软管和节点进行编号。将软管离散为n段,第i段软管长度为li,则有n+1 个节点,与加油吊舱相连的为0 号节点,第i个节点的质量为


图5 软管-锥套参考系示意图Fig.5 Reference frames of the hose-drogue system
式中:ρhose表示软管线密度,mhose表示锥套质量。
2.2 节点受力分析
对节点i进行受力分析,如图6 所示。图中Wi表示节点i所受重力,Ti表示软管内部张力,Qi表示软管所受气动力的合力,Fi表示软管微段之间由于弯曲产生的等效恢复力,则节点i的合外力Hi可表示为

图6 节点i 受力分析Fig.6 Force analysis for node i

2.3 气动力计算
不考虑加油机尾涡和受油机头波的影响,软管在空中稳定拖曳时所受到的气动力主要包括3 部分:软管末端的锥套⁃稳定伞组件产生的气动阻力、软管表面受到的空气摩擦阻力和压差阻力。软管微段受到的分布气动力可以用质心处的等效集中力代替,由于离散模型中的软管质量集中在两端球形铰链上,可进一步将质心处的集中力用两端球铰的等效力,如图7 所示。下面给出各部分气动阻力的计算方法。

图7 软管微段气动力等效示意图Fig.7 Equivalent figure of aerodynamic of the hose micro segment
2.3.1 锥套⁃稳定伞气动阻力
锥套⁃稳定伞组件产生的气动阻力可通过如下公式计算

式中:ρ∞表示来流密度,V表示当地速度,ddrogue表示稳定伞完全张开后直径,Cddrogue表示稳定伞的阻力系数,阻力方向与来流方向相同。
2.3.2 摩擦阻力
考虑空气的黏性作用,软管在加油机尾涡流场中运动时,周围气流的速度梯度会沿着软管表面产生分布的切向力,沿轴向积分便形成了软管所受到的摩擦阻力。圆柱体所受的摩擦阻力因数是雷诺数Re的函数,工程上可以通过Hoerner[12]实验得出的经验公式计算得出

式中:V表示气流相对于软管微段中心的速度;μ表示空气的运动黏性系数,值取1.46×10-5m2/s;L表示软管微段的特征长度,定义为

式中:dhose为软管外径,α为软管轴线与相对速度V的夹角。对第i节软管微段,相对速度V定义为

式中:Vabs表示气流相对地面的速度矢量,Vi-1、Vi分别表示第i-1、i个节点的速度矢量。
计算得出Cf后,软管微段的摩擦阻力Dskf可通过下式得到

式中:Vτ表示相对速度的切向分量,l表示软管微段的长度,摩擦阻力的方向与切向速度方向相同。
2.3.3 压差阻力
由于空气的黏性作用,气流流经加油软管时会在软管表面后部发生流动分离,导致在软管迎风面的压力比背风面要高,这种压力差形成了压差阻力。与摩擦阻力因数类似,压差阻力系数同样是雷诺数Re的函数,计算方法同样使用Hoerner 由实验得到的经验公式给出

压差阻力的方向与法向速度方向相同。
2.3.4 软管恢复力
软管在空中拖曳时会在气动阻力的作用下发生弯曲变形,软管内部产生一个恢复力矩,令软管产生抵抗弯曲的趋势,软管微段的受力情况可以简化为简支梁,内部的弯曲力矩可以通过一个作用在简支梁中间的集中载荷来代替[13⁃14],用等效恢复力Fei表示,如图8 所示。简支梁的两端可以在发生弯曲时自由旋转,对于节点i,等效恢复力的大小Fei与微段两端的扭转角θL、θR有关

图8 软管微段弯曲等效模型Fig.8 Equivalent model of the bending hose micro segment

式中:L表示软管微段的长度;E为软管的弹性模量;I为软管截面的几何惯性矩,可通过式(14)计算得出

式中:dhi表示软管内径直径,dho表示软管外径直径。
等效恢复力的方向为

扭转角θL、θR可通过式(16)计算得出。

3 变阻尼过程仿真模拟
3.1 流场计算方法验证
为了验证数值方法的可信度,对文献[15]中所使用的稳定伞建立三维模型,进行气动力数值模拟,并将数值模拟的结果与NASA 飞行试验数据进行对比。飞行试验中使用的锥套⁃稳定伞及对应的简化三维模型如图9 所示,数值模拟与实验对比结果如图10 所示。结果表明,所采用的数值方法得到的阻力值与实验数据吻合较好,佐证了数值方法的可信度,同时表明伞面透气性对于稳定伞整体阻力的影响不大。

图9 验证用CATIA 模型Fig.9 Paradrogue CATIA model for verificaion

图10 实验与仿真数据对比Fig.10 Comparison of operation and simulation data
3.2 数值仿真设置
空中加油系统要求设备能够在高度为海平面至40 000 英尺(约为12 000 m)范围,速度在370~550 km/h(约为0.3~0.5 马赫)范围内正常工作。本文仿真模拟环境主要在此范围之内,计算域选择底面半径为5 000 mm、高为15 000 mm 的圆柱形区域,选用四面体网格,如图11 所示。经过网格无关性验证后,网格总量超过300 万个时网格数对计算结果影响很小。在稳定伞附近进行网格加密,网格总量约400 万个。

图11 稳定伞流场网格Fig.11 Fluid mesh of paradrogue
3.3 数值仿真结果
本节给出了稳定伞气动力数值模拟的结果。根据稳定伞的阻力,分析了不同飞行速度和海拔高度下软管的拖曳形状。加油机的迎角为0°,来流方向如图5 所示,软管的各项参数如表1 所示。

表1 软管锥套参数Table 1 Parameters of hose⁃drogue
3.3.1 变速度气动特性
图12 和图13 分别是3 种伞撑角模型阻力特征与阻力随速度的变化趋势,从图12 中可以看出,当伞撑角从10°变化到20°的过程中,稳定伞的阻力特征可以从0.4 变化到1.1,变阻尼区间较大。图14是加装了3 种伞撑角模型后软管的拖拽形状,从图中可以看出,伞撑角为10°的模型适用的马赫数范围为0.5~0.6,15°模型适用的马赫数范围为0.4~0.6,20°模型适用的马赫数范围为0.3~0.5,3 种模型适用范围各不相同,同时又有重叠区域,伞撑角从10°变化到20°过程中可以完整覆盖马赫数0.3~0.6 的速度域。

图12 阻力特征-速度关系曲线Fig.12 Relationship between drag characteristic and velocity

图13 阻力-速度关系曲线Fig.13 Relationship between drag and velocity

图14 稳定伞拖拽位置Fig.14 Stable draught position of paradrogue
3.3.2 变高度气动特性
图15 和图16 分别是3 种伞撑角模型阻力特征与阻力随高度的变化趋势,图17 是加装了3 种伞撑角稳定伞后软管的拖拽形状。从图中可以看出,伞撑角为10°的模型适用范围为2 000~6 000 m,15°模型适用范围为2 000~10 000 m,20°模型适用范围为6 000~10 000 m。仅考虑高度的变化时,10°模型适用于低海拔、高密度区;20°模型适用于高海拔、低密度区;15°模型作为前两者过渡模型具有最广的高度适用范围。结果表明,伞撑角从10°变化到20°过程中可以完整覆盖2 000~10 000 m 的高度域。
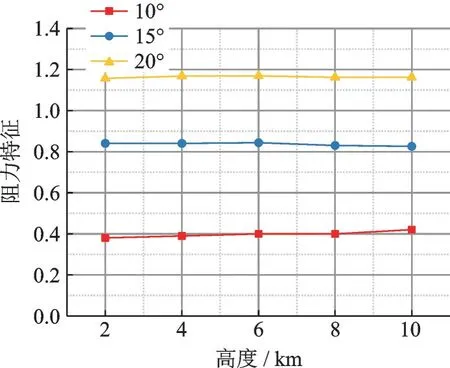
图15 阻力特征-高度关系曲线Fig.15 Relationship between drag characteristic and altitude

图16 阻力-高度关系曲线Fig.16 Relationship between drag and altitude

图17 稳定伞拖拽位置Fig.17 Stable draught position of paradrogue
4 结 论
仿真结果表明,单一考虑速度或高度的变化,通过改变稳定伞的伞撑角,可以控制阻尼特性的变化,使稳定伞能够覆盖更宽的速度域和高度域。10°模型由于阻力特征小,相同条件下产生阻力最小,因此可用于高速度、低海拔区域来降低产生的阻力值;20°模型阻力特征最大,产生阻力也最大,因此可用于低速度、高海拔等需要较大阻力的情况;15°模型作为前两者的过渡模型,可以保证所覆盖速度域和高度域的连续性。当速度和高度同时发生变化时,调节伞撑角可以有效控制加油锥套的下沉量,有效拓展了传统稳定伞的加油包线,对软式空中加油技术的应用有着显著的改善。
