设计参数及大气参数对降落伞充气性能的影响

贾贺 包进进 荣伟

（1 北京空间机电研究所，北京 100094）（2 南京航空航天大学航空学院，南京 210016）

0 引言

降落伞系统作为一种高效、可靠的回收手段，在我国载人飞船、返回式卫星以及月球探测、火星探测等回收或减速着陆过程中，都得到了广泛的应用[1-2]。随着探月工程月地高速再入返回试验任务的成功实施[3]，我国对于地外行星探测的研究也已经进入实质阶段。

地外行星的大气层的成分、物理性质与地球大气层存在着较大的差别，因此，针对地外行星大气环境下的降落伞系统设计需要考虑更多的影响因素，除了降落伞的设计参数外，大气参数对降落伞充气性能的影响是重中之重。然而，目前用来计算降落伞充气性能参数的经验公式对于地外行星，例如火星这样稀薄的大气环境将不再适用[4-6]。

国外对于降落伞工作过程的数值模拟研究已经比较深入[7-10]，国内使用LS-DYNA 软件对降落伞工作过程仿真的研究近十年也有了一定的进展[11-17]。本文以降落伞充气过程为研究对象，使用LS-DYNA 软件进行数值模拟，研究降落伞设计参数及大气参数对降落伞充气性能的影响情况；进一步验证使用LS-DYNA软件模拟充气过程的可行性，获得降落伞设计参数及大气参数对降落伞充气特性影响的一般规律，为后续用于外行星探测的降落伞系统设计提供一定的参考。

1 仿真模型的建立及仿真控制参数的选择

1.1 仿真模型的建立

（1）降落伞仿真模型的建立

根据文献[12]建立降落伞仿真模型，选用美国的经典伞型-C9 伞，伞型为平面圆形伞。对降落伞仿真模型做如下假设：模型为轴对称的结构；模型的初始形状为有一定的进气孔尺寸，截面为梅花形状的模型；模型只考虑伞绳的连接，对于伞衣径向带、顶孔绳等不做考虑，如图1 所示。Dc为伞衣的结构直径，Dv为伞衣的顶孔直径，Dp为伞衣的充满直径，hs为伞衣幅上顶点到底边的高度，hp为伞衣充满的高度，le为伞绳长度，es为伞衣幅底边长，N为伞衣幅数。

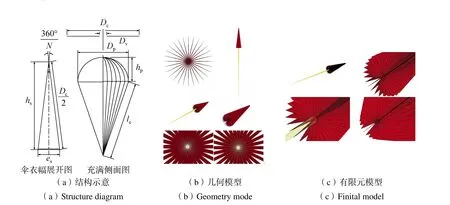
图1 降落伞模型Fig.1 Parachute model

伞衣材料选用美军标的MIL-C-7020III 材料，材料的密度为533.77kg/m3，弹性模量为0.4309GPa，泊松比为0.14，伞衣厚度为0.0001m；伞绳材料的密度为462.00kg/m3，弹性模量为97.0GPa。假设伞绳的横截面为圆形，面积为4.91×10–6m2。

在LS-DYNA 的前处理软件中对降落伞仿真模型进行有限单元的网格划分，得到降落伞的有限元模型。降落伞仿真模型的伞衣单元选择薄壳单元，伞绳选择离散的梁/索单元。

（2）流场几何模型的建立

根据文献[12]建立流场仿真模型，运用LS-DYNA 的前处理软件建立流场几何模型。对流场仿真模型做如下假设：不可压缩流场，符合N-S 方程；稳态定常流，即流体的速度方向恒定，且速度大小不变；外表面为与风洞壁性质一样的边界约束条件，如图2 所示。v为来流速度，Df为流场直径，Lq为流场前端面距伞绳汇交点的长度，Lh为未充气流场后端面距伞衣顶端的长度，Lf为流场长度。

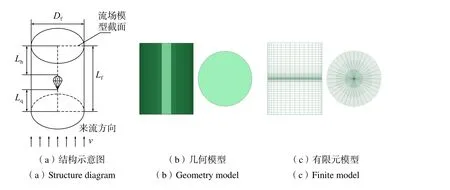
图2 流场模型Fig.2 Fluid model

流场仿真模型的流体定义为理想气体，满足理想气体状态方程。气体的密度为1.18kg/m3，动态粘度系数为1.7456×10–5，气体的比热容比（γ）为1.4。

同样，在LS-DYNA 前处理软件中，根据有限元网格划分的基本原则对流场的几何模型进行有限单元的网格划分，得到流场的有限元模型。流场仿真模型的单元选择体单元。流体单元算法是单点ALE 多物质单元方程。

1.2 仿真控制参数的选择

在LS-DYNA 中，结构模型与流体模型之间的耦合关系是通过关键字的参数设置来定义的，选用最优化的控制参数值对仿真过程的实现起着决定性作用。本文在数值模拟降落伞充气过程时，所采用的流固耦合过程的控制关键字见文献[18-19]。

2 降落伞设计参数对降落伞充气特性的影响及分析

2.1 伞绳长度对降落伞充气特性的影响

在LS-DYNA 软件中，选用平面圆形伞-C9 伞作为研究对象，对伞绳长度分别为6m、9m、12m 的三种降落伞仿真模型进行仿真，得到了三种不同的伞绳长度状态下充气特性的情况。

（1）伞绳长度对伞衣投影面积变化的影响

三种不同伞绳长度的伞衣投影面积（At）与名义面积（Ao）比（以下简称伞衣投影面积比）随充气时间（tf）的变化情况如图3 所示。

由图3 中可以看出，伞绳长度为6m 的伞衣投影面积比最大的时候为0.3 左右，充气稳定后，伞衣的投影面积比大概保持在0.25 左右；而伞绳长度为12m时，伞衣投影面积比最大时可以达到0.52，稳定后保持在0.48 左右。可见，随着伞绳长度的增长，伞衣的投影面积比增大。

图3 不同伞绳长度的伞衣投影面积比的变化Fig.3 The change of the projection area ratio of parachute in different lengths

（2）伞绳长度对充气时间的影响

同样，从图3 中还可以看出，伞绳长度为6m 的仿真模型在0.13s时伞衣外形形状达到最大值，在0.28s时伞衣的充气形状基本达到稳定状态，充气全过程完成；而对于伞绳长度为12m 的仿真模型，其外形形状在0.18s时才达到最大值，但是其在0.24s时伞衣就基本达到稳定状态，完成了充气的整个过程。可见，随着伞绳长度的增长，伞衣充气稳定的时间减小。

（3）伞绳长度对充气特性影响的分析

通过LS-DYNA 中的数值模拟，发现随着伞绳长度的增长，伞衣投影面积与名义面积比增大，最终达到稳定状态的时间减小。这是因为当伞绳长度增长时，阻碍伞衣底边张开的作用力减小，使得伞衣的充气过程可以更快地达到稳定状态。

2.2 伞衣透气量对降落伞充气特性的影响

由文献[8-9]可知，在LS-DYNA 软件中，是通过定义关键字*CONSTRAINED_LIS 中的粘性系数（a1）和惯性系数（b1）两个控制参数来表征降落伞伞衣织物透气性的。已知伞衣材料美军标MIL-C-7020 III 型尼龙材料的a1为1.599×106kg/m3s，b1为4.805×105kg/m4。

选用三种伞衣透气量参数进行仿真（选取三种不同的a1和b1值），即1/2 的MIL-C-7020 III 透气量值、MIL-C-7020 III 的标准透气量值和2 倍的MIL-C-7020 III 的透气量值，得到了三种不同伞衣透气量状态下充气特性的情况。

（1）伞衣透气量对伞衣投影面积变化的影响

三种不同伞衣透气量的伞衣投影面积与名义面积比随充气时间的变化情况如图4 所示。

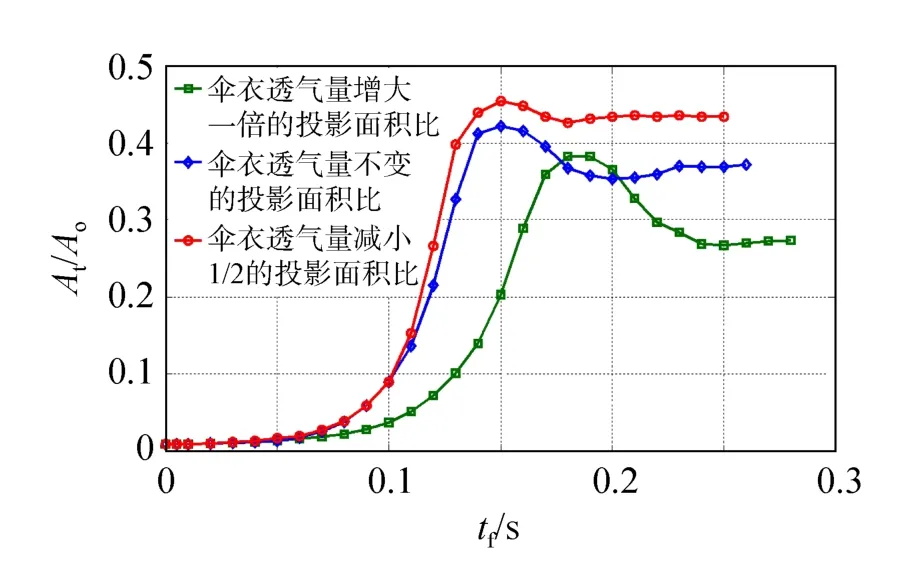
图4 不同伞衣透气量的伞衣投影面积比的变化Fig.4 Changes of projection area ratio of parachute in different air permeability

由图4 中可以看出，2 倍伞衣透气量值的伞衣投影面积比最大值可以达到0.38，充气过程稳定后，也可以维持在0.28 左右；而1/2 伞衣透气量值时，伞衣投影面积比最大时可以达到0.46，稳定后保持在0.43左右。可见，随着伞衣透气量的减小，伞衣充得更满，伞衣的投影面积比增大。

（2）伞衣透气量对充气时间的影响

同样，从图4 中还可以看出，2 倍伞衣透气量值的降落伞仿真模型在0.19s时伞衣外形形状达到最大值，在0.28s时伞衣的充气形状基本达到稳定状态，充气全过程完成；而对于1/2 伞衣透气量值的降落伞仿真模型，其外形形状在0.15s时就已经达到最大值，并且其在0.21s 左右伞衣就基本达到稳定状态，完成了充气的整个过程。可见，随着伞衣透气量的增大，伞衣充气稳定的时间增大。

（3）伞衣透气量对充气特性影响的分析

通过上述在LS-DYNA 中的数值模拟，可以很清楚地发现随着伞衣透气量的增大，伞衣投影面积与名义面积比减小，充气时间增大。其原因是因为当伞衣透气量增大时，会导致在充气过程中伞衣内部气体的体积增量减小，使得伞衣充气的过程变缓，伞衣则需要更长的时间才能达到稳定状态，同时还会导致伞衣投影面积比减小，即伞衣的充气形状在伞衣达到稳定状态后依然不是很饱满。

2.3 伞衣名义直径对降落伞充气特性的影响

（1）伞衣名义直径对伞衣投影面积变化的影响

选用降落伞仿真模型的伞衣名义直径分别为4.2m、6.2m 和8.5m。对三种不同伞衣名义直径的仿真模型进行数值模拟，得到其伞衣投影面积与名义面积比随充气时间的变化情况，如图5（a）所示。可以看出，伞衣名义直径不同，三种仿真模型的伞衣投影面积比稳定时都在0.35 左右。但是三种模型伞衣投影面积比的变化曲率却有所差别，如图5（b）所示。无因次充气时间（T）为降落伞工作时间（t）与降落伞充气时间的比（T=t/tf）。

随着伞衣名义直径的增大，伞衣投影面积比的变化曲率不断的增大。当伞衣名义直径为4.2m时，伞衣投影面积比在0.11s 左右就达到了最大值，变化较为剧烈；而当伞衣名义直径为6.2m时，伞衣投影面积比在0.15s时才达到最大值。可见，随着伞衣名义直径的增大，伞衣投影面积比的变化有逐渐变缓的趋势。

图5 不同伞衣名义直径的伞衣投影面积比Fig.5 The projection area ratio of different parachute nominal diameters

（2）伞衣名义直径对充气时间的影响

同样由图5（a）中还可以看出，伞衣名义直径为4.2m 的仿真模型在0.11s时伞衣外形形状达到最大值，即伞衣第一次达到最大外形状态的充气时间为0.11s，且伞衣在0.16s 左右就达到了稳定状态，充气过程完成；而当伞衣名义直径为6.2m 的仿真模型在0.15s 才达到伞衣外形形状的最大值，并且在0.20s 左右达到稳定状态，即其完成稳定状态充气的时间为0.20s。可见，随着名义直径的增大，伞衣达到充气稳定状态的时间相应的增大。

（3）伞衣名义直径对充气特性影响的分析

通过对不同伞衣名义直径的仿真模型在LS-DYNA 中的数值模拟，可以发现，随着伞衣名义直径的增大，充气时间增大。其原因是因为当伞衣名义直径增大时，其充气时需要的伞衣内部的气体体积增大，但由于速度恒定，体积的变化率没有太大的增加，就使得伞衣的充气过程变得比较缓慢，伞衣投影面积与名义面积比的变化曲率增大。

3 大气参数对降落伞充气特性的影响及分析

3.1 流场速度对降落伞充气特性的影响

采用相同的降落伞仿真模型（平面圆形伞-C9 伞）在流场速度分别为40m/s、80m/s 和120m/s 三种状态下数值模拟其充气过程。

（1）流场速度对伞衣投影面积变化的影响

三种不同流场速度下，伞衣投影面积与名义面积比随充气时间的变化情况如图6（a）所示，可以看出，流场速度不同，对伞衣投影面积比稳定时的最终值影响不大。三种流场速度下，在伞衣达到充气稳定状态时的伞衣投影面积比都在0.36 左右。但是对伞衣投影面积比的变化曲率影响比较大，如图6（b）所示，随着流场速度不断的增大，伞衣投影面积比的变化曲率不断的减小。当流场速度为120m/s时，伞衣投影面积比在0.12s 左右就达到了最大值，变化很剧烈；而当流场速度为40m/s时，伞衣投影面积比在0.25s时才达到最大值。可见，随着流场速度的增大，伞衣投影面积比的变化更加剧烈。

图6 不同流场速度的伞衣投影面积比Fig.6 The projection area ratio of canopy in different velocity of flow field

（2）流场速度对充气时间的影响

从图6（a）中还可以看出，流场速度为40m/s 的仿真模型在0.30s时伞衣外形形状达到最大值，伞衣在0.36s 左右达到了稳定状态，充气过程完成；而流场速度为120m/s 的仿真模型则在0.13s 就达到了伞衣外形形状的最大值，即伞衣第一次达到最大外形状态的充气时间为0.13s，伞衣在0.19s 左右就达到了稳定状态，即其完成稳定状态充气的时间为0.19s。可见，随着流场速度的增大，伞衣达到充气稳定状态的时间相应的减小。

（3）流场速度对充气特性影响的分析

通过上述的数值模拟，可以很清楚地发现随着流场速度的增大，充气时间减小。其原因是因为当流场速度增大时，会导致在充气过程中伞衣内部气体的体积增量增大，使得伞衣的充气过程可以较为迅速的完成，伞衣投影面积与名义面积比的变化曲率减小。同时，还可以发现在LS-DYNA 中流场速度增大时，获得的充气时间与理论值的误差较小；而在流场速度减小时，获得的充气时间与理论值却有一定的差距，这主要是因为对流场的设置还有一些需要改进的参数，导致对流场的控制不能完全达到理想状态。

3.2 大气密度等对降落伞充气特性的影响

（1）大气气密度等对伞衣投影面积变化的影响

本文采用相同的降落伞仿真模型（平面圆形伞-C9 伞）在三种不同的气体状态参数下数值模拟其充气过程。三种大气密度等气体状态参数的设置如表1 所示[20]。

表1 气体状态参数设置Tab.1 Atmospheric parameters settings

在三种不同的气体状态参数设置下，伞衣投影面积与名义面积比随充气时间的变化情况如图7（a）所示。

图7 不同气体状态参数的伞衣投影面积比Fig.7 The projection area ratio of canopy in different atmospheric parameters

由图7（a）中可以看出，气体状态参数不同，主要是密度的不同，对伞衣投影面积比稳定时的最终值影响不大。三种气体状态参数下，在伞衣达到充气稳定状态时的伞衣投影面积比都在0.36 左右。但是其对伞衣投影面积比的变化曲率影响比较大，如图7（b）所示，随着大气密度的不断减小，模拟的高度不断增大，伞衣投影面积比的变化曲率不断增大。当模拟高度为6km时，伞衣投影面积比在0.22s 左右才达到最大值，其变化曲率较0km 的时候增大了些；而当模拟高度为12km时，伞衣投影面积比在0.29s时才达到最大值，其变化曲率较前两者而言，又增大了不少。可见，随着高度的增大，伞衣投影面积比的变化曲率有增大的趋势。

（2）大气密度等对充气时间的影响

同样，从图7（a）中还可以看出，模拟高度为6km 的仿真模型在0.22s时伞衣外形形状达到最大值，但是伞衣在0.34s 左右才达到稳定状态，充气全过程完成；而当模拟高度为12km时的仿真模型则在0.29s才达到了伞衣外形形状的最大值，并在0.38s 左右达到了伞衣的稳定状态。可见，随着模拟高度的增大，大气密度的减小，充气时间增大，伞衣达到充气稳定状态的时间也跟着增大。

（3）大气密度等对充气特性影响的分析

通过上述三种气体状态参数下对仿真模型在LS-DYNA 中的数值模拟，可以很清楚地发现随着模拟高度的增大，大气密度的减小，充气时间增大。究其原因，是因为当大气密度减小时，其动压会相应的减小，使得伞衣的充气过程变得比较缓慢，伞衣投影面积与名义面积比的变化曲率增大。

4 结束语

通过数值模拟可知，降落伞设计参数及大气参数对充气性能影响的一般规律如下：

1）随着伞绳长度的增长，充气时间减小，伞衣投影面积与名义面积比增大；2）随着伞衣透气量的增大，充气时间增大，伞衣投影面积与名义面积比减小；3）随着伞衣名义直径的增大，充气时间增大，伞衣投影面积比的变化曲率增大；4）随着流场速度的增大，充气时间减小，伞衣投影面积与名义面积比的变化曲率减小；5）随着模拟高度的增大，大气密度的减小，充气时间增大，伞衣投影面积比的变化曲率增大。

本文分析得到的上述降落伞设计参数及大气参数对充气性能影响的规律，进一步验证了使用LS-DYNA 软件数值模拟降落伞充气过程的可行性，为后续研究地外行星探测用降落伞系统的充气性能提供了一种新的分析手段。