基于成本的机载通信系统可靠性安全性一体化设计

刘睿禹，吴红兰，陶旭东

（南京航空航天大学民航学院，南京 211106）

航空电子系统是飞机的“大脑”，对于民用客机有着“神经中枢”的关键作用，其综合化程度决定了飞机的性能和发展水平，至今已经历4 代典型技术发展[1]。机载通信系统作为民用客机的关键航电系统之一，其子系统包括高频通信系统、甚高频通信系统、卫星通信系统、内话通信系统、应急发射系统等，承担着飞机语音通信、数据传输、语音记录与应急发射等关键功能，对整机的安全性、可靠性至关重要[2]。对于广泛运用新技术的系统研发，通信系统具有更高的安全性与可靠性要求，代价则是过高研发成本。如何在保证系统安全性与可靠性的前提下约束降低研发成本，在三者之间进行分配权衡是本文的主要研究目标。

在机载通信系统可靠性安全性研究方面，江玉峰基于机载语音通信系统搭建了较为完善的故障树，研究了系统可靠性与安全性的内在关系[3]。孙毅刚等[4]针对机载航电系统性能指标分配问题，提出了一种基于序列二次规划的性能指标优化分配方法。Susova 与Petrov[5]首次运用马尔可夫模型对飞机系统的可靠性与安全性进行权衡分析。Gürsu[6]针对机载通信系统搭建了通用可靠性分析框架，并对现有的飞机无线通信技术进行了可靠性的对比分析。

在研制成本方面，吕文涛等[7]运用TruePlan⁃ning 成本估算系统模型搭建了航电系统制造成本与可靠性之间的数学模型。王发丽[8]从不同层次详细分析了飞机研制项目成本的影响因素，在此基础上建立了参数法成本估算模型。Assidmi[9]提出一种系统思维方法成本增长估计系统生命周期成本，将研制成本纳入全寿命周期成本进行分析。Castagne 等[10]面向飞机机身提出了一种运用分层技术与线性规划算法，在早期设计阶段引入成本影响作为设计参数，从而进行集成来估算研制阶段的成本影响的方法。Lammering[11]基于飞机详细设计参数，提出了一种评估飞机初步设计成本和收益的新方法，并搭建了成本与参数之间的非线性数学模型。该模型可以估算飞机单位成本以及开发和生产的非重复和重复性成本。

在一体化设计方面，褚双磊等[12]运用线性加权评分模型，对飞机多目标性能参数进行优化，一体化评估了整机的性能。Chanchal 等[13]基于可靠性与维修性，针对直升机的全寿命周期成本，搭建了三者之间的数学模型，分别从定性与定量的角度做了一体化分析。Das 等[14]提出了一种面向设备单元制造系统设计的多目标混合整数规划模型，该模型最大程度地降低系统总成本，并实现设备单元可靠性最优化。

基于上述背景，本文首先确定通信系统安全性与可靠性量化指标与分配方法，进而以民用客机通信系统为例，运用灰色线性回归关联模型确定影响共性因子，最后运用多元线性规划与无量纲评估模型进行一体化权衡寻优，并运用基于核与灰度的灰色马尔科夫预测模型结果对比寻优结果进行验证。

1 通信系统安全性、可靠性与成本量化指标

安全性关注系统不发生以及引发事故的能力，目的在于防止事故发生，避免人员伤亡与财产损失，侧重于故障发生后对系统的影响；可靠性着眼于维持系统功能的正常发挥，实现系统目标，侧重于研究故障发生之前到故障发生为止的系统状态。

同时，两者之间的联系也非常密切：可靠性分析是开展安全性评估的基础，可靠性目标与指标的确定与优化往往是基于最低可接受的安全性水平开展的。同时可靠性活动为安全性活动提供底层的可靠性数据与信息，以支持安全性设计、确认与验证工作的开展。可靠性的数据与相关的可靠性预计分析还能为系统某些特定的安全性要求提供最有力的证明。

安全性、可靠性量化指标是系统的安全性、可靠性的度量，是系统安全性工作的基础和重要参考标准，本节首先确定量化指标，为后文一体化设计做好铺垫。

1.1 安全性量化指标的确定

安全性作为民航业的生命线，若发生安全性事故则可能造成重大的财产损失、飞机损毁甚至是人员伤亡。对系统安全性进行设计与评估的重要性不言而喻，系统安全性没有满足相关的适航标准，对于其研制成本与可靠性水平的优化分析也就无从谈起。在研究基于成本的可靠性安全性一体化设计过程中，首先确定了机载通信系统的安全性基本要求，并将其设为后文多目标优化的固定约束条件。

为提高衡量安全性目标的可操作性，适航咨询通告（AC）25.1309 综合考虑失效状态对飞机的影响、乘客和机组人员的影响，确定失效状态的严重程度[15],表1 列出了失效状态严重程度类别以及对应的影响描述与定性定量概率要求。

表1 失效状态严重程度类别与定性定量概率Table 1 Severity category of failure state and qualitative and quantitative probability

根据联邦航空条例（FAR）25 部、中国民航规章（CCAR）25 R4《运输类飞机适航标准》F 分部25.1309 条，对飞机系统安全性设计做了如下要求：（1）发生任何妨碍飞机继续安全飞行于着陆的失效状态的概率为极不可能；（2）发生任何降低飞机能力或机组处理不利运行条件能力的其他失效状态的概率为不可能。民用航空产品技术标准规定（CTSO）C59b 部分对机载通信系统的失效状态做出了如下要求：（1）本CTSO 定义的功能丧失属微小的失效状态。对于主通信系统和应急通信系统，跨洋/远距离运行的风险是微小的；（2）设备的设计保证等级应至少与这种失效状态类别相对应。

本文对于机载通信系统的安全性分析以及优化是在满足国内外相关适航标准的前提下进行的，通信系统故障对应微小失效状态的Ⅲ类故障，则是CTSO 标准所允许最低的安全性要求。但在实际情况中，机载通信系统一般对应Ⅳ、Ⅴ类失效状态，综上，对于安全性指标的定量概率要求应在10-5/飞行小时与10-3/飞行小时水平之间。

目前我国在整机级与系统级常用的安全性指标参数有：平均事故间隔时间、事故率（事故概率）、安全可靠度和损失率（损失概率）。4 个参数彼此之间存在着一定的联系，但侧重点不同：安全可靠度取决但不同于事故概率，其更关注灾难性事故，对其他严重等级的事故考虑较少，并且衡量的时间范围为系统的工作时间，而不是系统的全寿命周期；损失率是事故率特例，但前者关注侧重点是灾难性事故，而后者则囊括几乎所有严重程度的事故，故障率则覆盖内容更广泛，与事故率不同在于其关注系统所有的故障，不论造成事故与否[16]。

民用客机安全性参数大多以事故作为研究对象，导致不易衡量，而直接测试系统的安全性成本代价过高。上文所列出的4 种常用安全性参数均为统计参数，如果限制其统计范围，则可以提供顶层的安全性要求。鉴于传统安全性参数的局限性，可尝试用故障率、失效率等指标来代替。

根据安全性指标要求与实际情况，对应表1 中的系统失效状态的定量概率要求，本文使用故障率通过量化指标的运算评价飞机系统安全性。

1.2 可靠性量化指标的确定

民用客机通信的根本目的是及时准确地完成传递、交换飞行相关信息与数据的任务。衡量民用客机通信系统性能的一个重要指标是高可靠性，一般系统的可靠性指标主要有平均故障间隔时间(MTBF)[17]，对于数字通信系统，其特有的可靠性指标为传输误码率。

平均故障间隔时间，是指产品或系统在两相邻故障间隔期内正确工作的平均时间，也称平均无故障工作时间，它是标志产品或系统能平均工作多长时间的量。对于民用客机，平均故障间隔时间作为可靠性指标是具有普适性的，既可用于评估整机级可靠性，亦可用于评估系统、子系统与设备的可靠性，是非常具有代表性的可靠性指标，在量化上也有比较成熟的技术支撑。

在实际传输数据的情况中，飞机通信出现误码是比较正常的现象，由于其通信间隔短，且传输质量不断改善，消除误码的方式日益成熟，目前民用客机的通信系统误码率浮动已经对系统以及飞机安全性几乎没有影响，所以不选用误码率作为系统可靠性指标。综上，本文选用普适性强的平均故障间隔时间作为通信系统可靠性指标。

1.3 成本指标的确定

目前，对于民用客机的成本分析，国内外学者一般按照全寿命周期的不同阶段进行划分，本文面向机载通信系统的研制阶段开展研究。

对于一般的飞机系统，研制成本一般由计价成本和不可预见成本组成，其中计价成本由研制过程中产生的设计费、材料费、外协费、专用费、试验费、固定资产使用费、人员薪资、管理费等8 项内容构成[18]，在研制项目成本管理过程中，要求不可预见成本不超过计价成本的5%。因此，计价成本占总体系统研制成本的95%以上，在本研究中不可预见成本可以忽略不计，由上述8 项费用构成的计价成本可视作成本指标，下文中均略写为成本，均指上述8 项成本费用总和。

2 共性影响因子分析

民用客机通信系统的高安全性、可靠性是多种因素综合影响的结果，而为了实现权衡模型的简洁性和可操作性，在进行研究时往往只选取数个重要的影响因素，而没有必要且不可能将所有因素都纳入预测模型中。由于民用客机通信系统的结构与研发过程属于综合航电系统的一部分，各通信子系统的研发过程、安全性要求、研发成本需要均不相同，也没有一个完整的关于飞机通信系统研发过程影响因素划分的记载。根据对机载通信系统进行不同失效模式的故障树分析，首先对通信系统研制阶段的可靠性、安全性影响参数进行归纳，共4 项一级影响因子，11 项二级影响因子，如图1 所示。

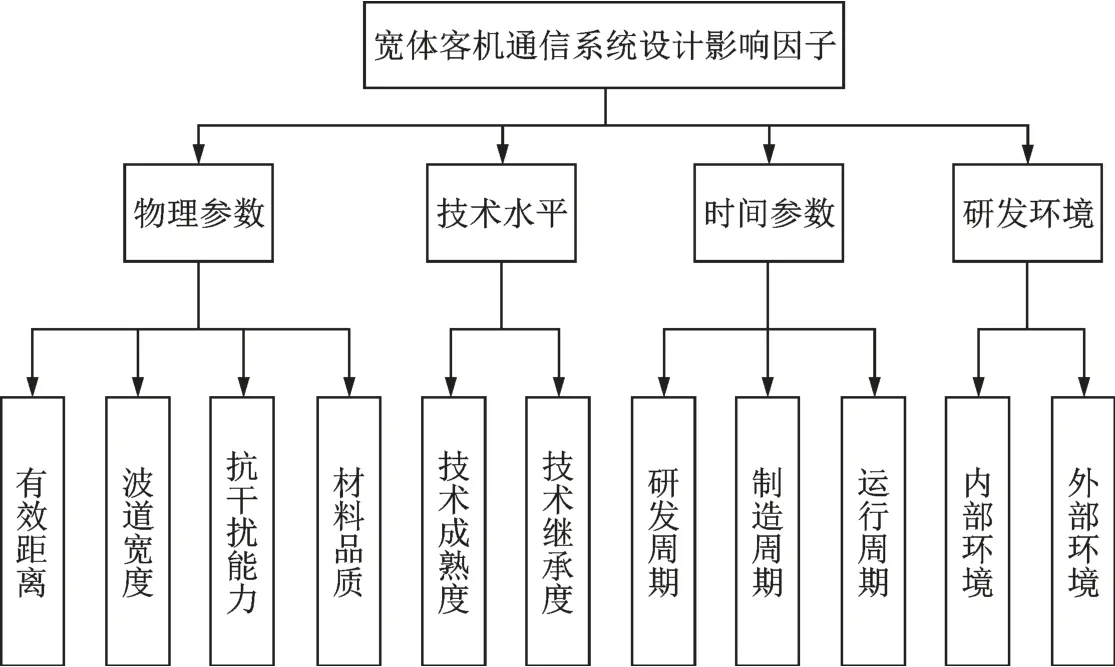
图1 通信系统研发影响共性因子Fig.1 Common factors influencing communication system development

2.1 共性因子灰色关联分析

灰色关联分析是基于各影响因子描绘的曲线几何结构与目标序列描绘曲线的相似性判断其联系的紧密程度这一基本思想。曲线越偏离，说明影响因素与历史数据序列之间关联度就越小，反之同理。灰色关联分析法对数据序列内部规律性或样本量没有限制，且相对计算量较少，操作简单方便，不会出现结果不相符合的情况[19]。其中关联度能够准确反映影响因素的作用程度，一般关联度在0.5 以下的指标可以被直接剔除。首先基于研发成本通过灰色关联分析处理共性因子，得到关联度排序。

步骤1 确定分析数列。本文采取市场上8 种民用客机通信系统构型的研发成本数据作为参考序列Y={Y(k)|k=1,2,…,8}，将这些系统的11 项共性影响因子的相对评分值作为目标序列Xi={Xi(k)|k=1,2,…,8},i=1,2,…,11。

步骤2 将共性影响因子无量纲化。由于系统中各因素列中的因子因量纲不同，且部分因子难以量化，不便于比较或在比较时难以得到正确的结论，故先将绝对参数转化为统一的相对参数，根据ATA 第23 章相关要求，为更好地表示参数评价水平，本文作者提出将相对参数范围确定为0～15，具体化分标准见表2。

表2 共性因子无量纲量化范围Table 2 Dimensionless quantitative range of common factors

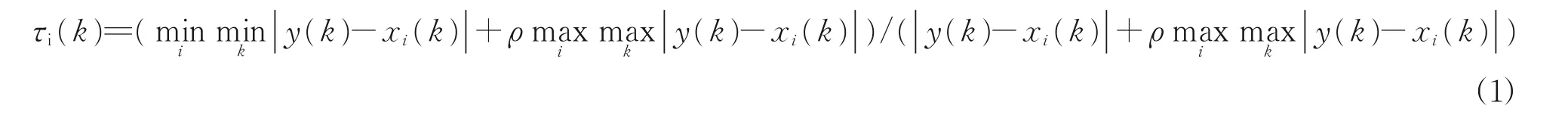
步骤3 计算灰色关联系数。Y(k)与Xi(k)的灰 色关联系数计算公式如下式中：ρ为分辨系数，ρ越小，分辨力越大，一般ρ的取值区间为(0,1)，具体取值可视情况而定，通常取ρ=0.5。根据步骤2 给出的评分标准与8 种典型民用客机机型通信系统研发成本以及共性因子实际评分情况代入式（1）计算得到。

步骤4 得到准确灰色关联系数。因为关联系数是比较数列与参考数列在各个时刻的关联程度值，所以它的结果值不止一个，而信息过于分散不便于进行整体性比较。因此有必要将各个时刻（即曲线中的各点）的关联系数集中为一个值，即求其算数平均值，作为比较数列与参考数列间关联程度的数量表示，最后对关联度进行排序，关联度公式如下

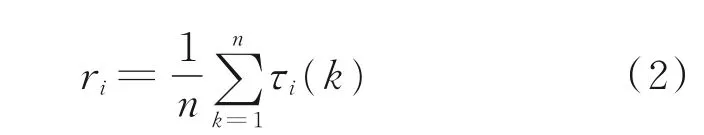
根据计算，11 项共性因子的关联度排序如表3所示。

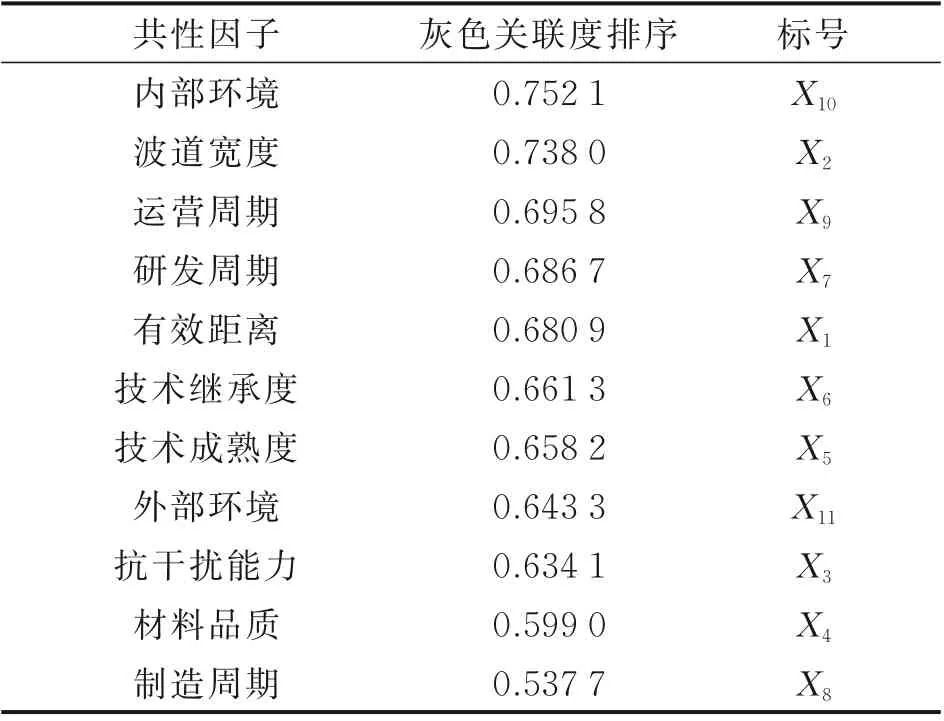
表3 共性因子灰色关联度排序Table 3 Ranking of common factors by gray correlation degree

首先由表可知各共性因子与通信系统的研发成本之间的灰色关联度均高于0.5，证明均与系统研发成本有强的关联，证明了共性因子归纳划分的合理性；其次，以关联度0.6 为基准，共有内部环境、波道宽度等9 项共性因子是关联较为紧密的。

2.2 共性因子多元回归分析

通过上节的灰色关联分析，证明了共性因子归纳的合理性，并筛选了关联度较高的9 项因子，本节采用多元线性回归法，确定各因子与系统成本的具体映射关系，建立相应的回归方程，得到预测公式。通过影响权重因子的重要程度筛选，在灰色关联分析的基础上，对11 项关联度高的因子进行线性回归处理，确定综合相关系数排名前六的因子，进而精简函数关系，将6 项因子再进行线性回归分析得到回归方程，经过数值检验，拟合度较高，表明函数表达式合理。

首先建立多元线性回归方程

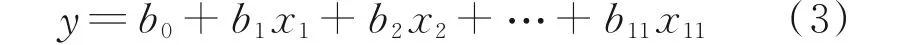
剔除低关联度因子x4与x8后，对余下9 项因子进行处理，同样以通信系统高成本为应变量，b0为常数项，b1，b2，…，b11为回归系数，是自变量每增加一个单位x对应变量y产生的影响效应，即x对y的偏回归系数；经过计算得到回归系数绝对值排前6 位的因子如表4 所示。

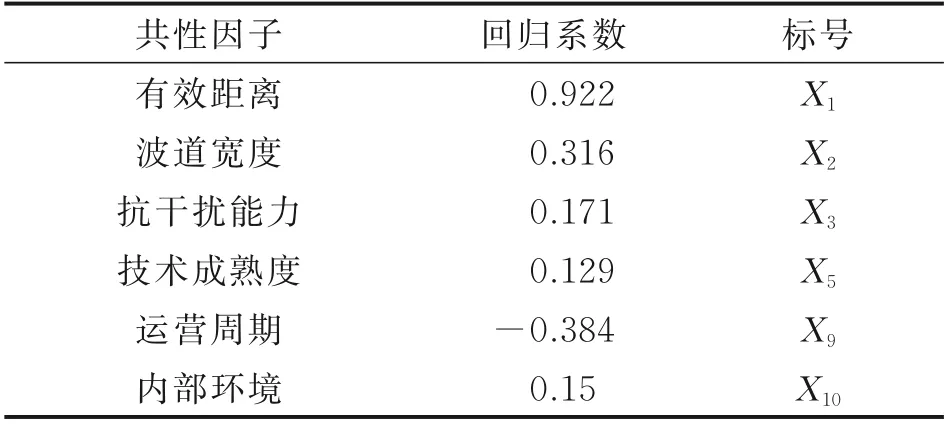
表4 共性因子回归系数Table 4 Regression coefficient of common factors

得到标准化多元线性回归方程

式中，通信系统有效距离与成本成正比，波道宽度与成本成正比，抗干扰能力与成本成正比，技术成熟度与成本成正比，运营周期与成本成反比，内部环境与成本成正比。回归方程得到的拟合度R2=0.875，证明上述6 项共性影响参数能够很好地解释对成本的影响，通过灰色关联分析⁃多元线性回归分析得到的共性因子是合理可行的。

根据确定的6 项主要共性因子与民用客机通信系统故障率与平均故障间隔时间数据，同样运用多元线性回归分析得到关于平均故障时间的标准化回归方程，拟合度R2=0.916，拟合效果较好，标准化回归方程为

3 项回归方程的平均拟合度为R△=0.852，运用灰色线性回归关联模型分析的总体效果较好。

3 一体化权衡寻优分析

基于成本对民用客机通信系统进行可靠性安全性一体化权衡，其中关键的步骤即一体化权衡寻优。根据上文拟合归纳出的量化回归方程关系，在一定的约束条件下寻找优化解域，并对不同域进行权衡对比。

首先，给表4 中6 项共性因子量化值界定范围，运用表2 给出界定某型客机通信系统各项参数评分范围，联系实际研制需要，给出表5 中相关约束范围预设值。

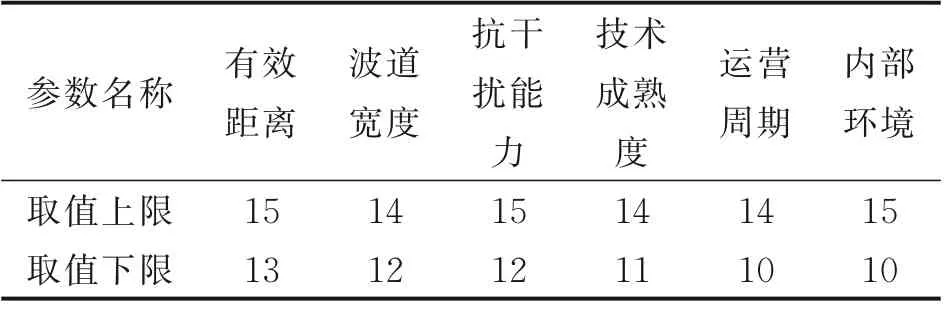
表5 一体化权衡寻优模型约束条件范围Table 5 Constraint range of integrated tradeoff optimi‑zation model

3.1 单目标寻优

根据多元线性回归方程，运用MATLAB 软件实现线性规划寻优，由表5 中的约束范围，首先通过线性规划得到单目标优化值。3 个单目标线性寻优方程运用2.2 节中进行共性因子筛选后得到的标准化回归方程，其中以成本为目标的寻优方程为式（4），以MTBF 为目标的寻优方程为式（5），以故障率为目标的寻优方程为式（6），6 项共性因子作为寻优方程变量，计算结果如表6 所示。

表6 单目标寻优结果Table 6 Single objective optimization results

根据单目标寻优结果，可以分析出三者之间的动态关系，当研制成本最优时，也就是成本最低为6 023.8 万元，系统平均故障间隔时间为95 841 h，故障率为5.96e-5，可知虽然节省了成本，但是设计得到的系统可靠性、安全性指标值相对较低。

当平均故障间隔时间最优时，即时长最长171 839 h，可靠性最好，系统研制成本为11 401.2 万元，故障率为4.53e-5，由于可靠性与安全性两者有一定的相关程度与趋势，所以在MTBF 值最大时，故障率相应地下降，但研制成本大幅增加。

当故障率最低为2.18e-5，系统安全性最好时，系统研制成本为14 044.3 万元，MTBF 值为158 423 h，故障率在最低时，成本有很大幅度增加，同时平均故障时间间隔也大幅增加。

3.2 多目标寻优模型

民用客机通信系统的可靠性、安全性权衡一体化验证就是要在满足系统性能要求的基础上，在共性因子约束条件范围内，确定可靠性与安全性最优值，使系统性能尽可能达到飞机用户的使用要求且控制成本。本节考虑的多目标优化问题可以描述为：3 个设计变量、6 个飞机性能约束条件与给定的约束范围，多目标函数为可靠性、安全性尽可能高，所对应的系统研制成本尽可能低，最终构建了一个多目标优化模型。

由于机载通信系统有系统冗余，设备级也存在新技术设备的不均匀冗余，若全部加以分析则过于复杂，不宜呈现对比趋势关系，此处默认为独立一套通信系统，暂时排除冗余系统以及冗余设备的影响。

在以平均故障间隔时间、研制阶段成本、故障率为多目标进行优化时，首先将3 个目标函数的权重都设置为1。对单目标进行归一化处理，使3 个单位不同的目标函数在取值处于相同水平。本文运用加权指数ZETA 评分模型进行综合评估，模型公式如下

表7 目标函数基准值Table 7 Benchmark value of objective function

由于成本的优化趋势为降低，故障率的优化趋势也为降低，平均故障间隔时间优化趋势为升高，3个目标趋势不同，所以式(7)中的基准值分数位置不同。

上文进行的线性规划单目标寻优是较为片面的，也是实际要求差距较大。对于可靠性、安全性一体化验证实质上是要寻找权衡域，根据表5 给出的约束条件，结合式（7）模型，通过多元线性规划寻优，得到多目标优化结果如表8 所示。

对于表8 给出各个次优值的量化参数值，明显有两个区域的权衡选择，优化值1、2、3 基本属于同一个权衡域，次优值4、5 属于一个权衡域，对比来看前者相对于后者平均成本节省了39%，但平均故障间隔时间减少了37.3%，故障率提高了 22.4%，对比数据的柱状图如图2 所示。

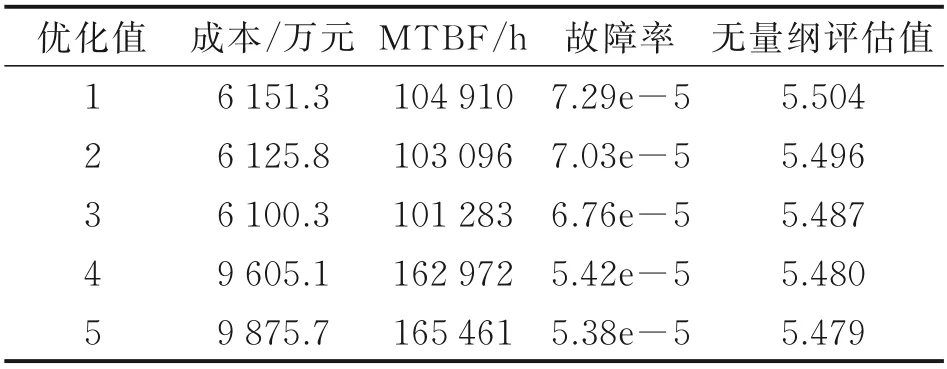
表8 多目标寻优结果Table 8 Multi‑objective optimization results

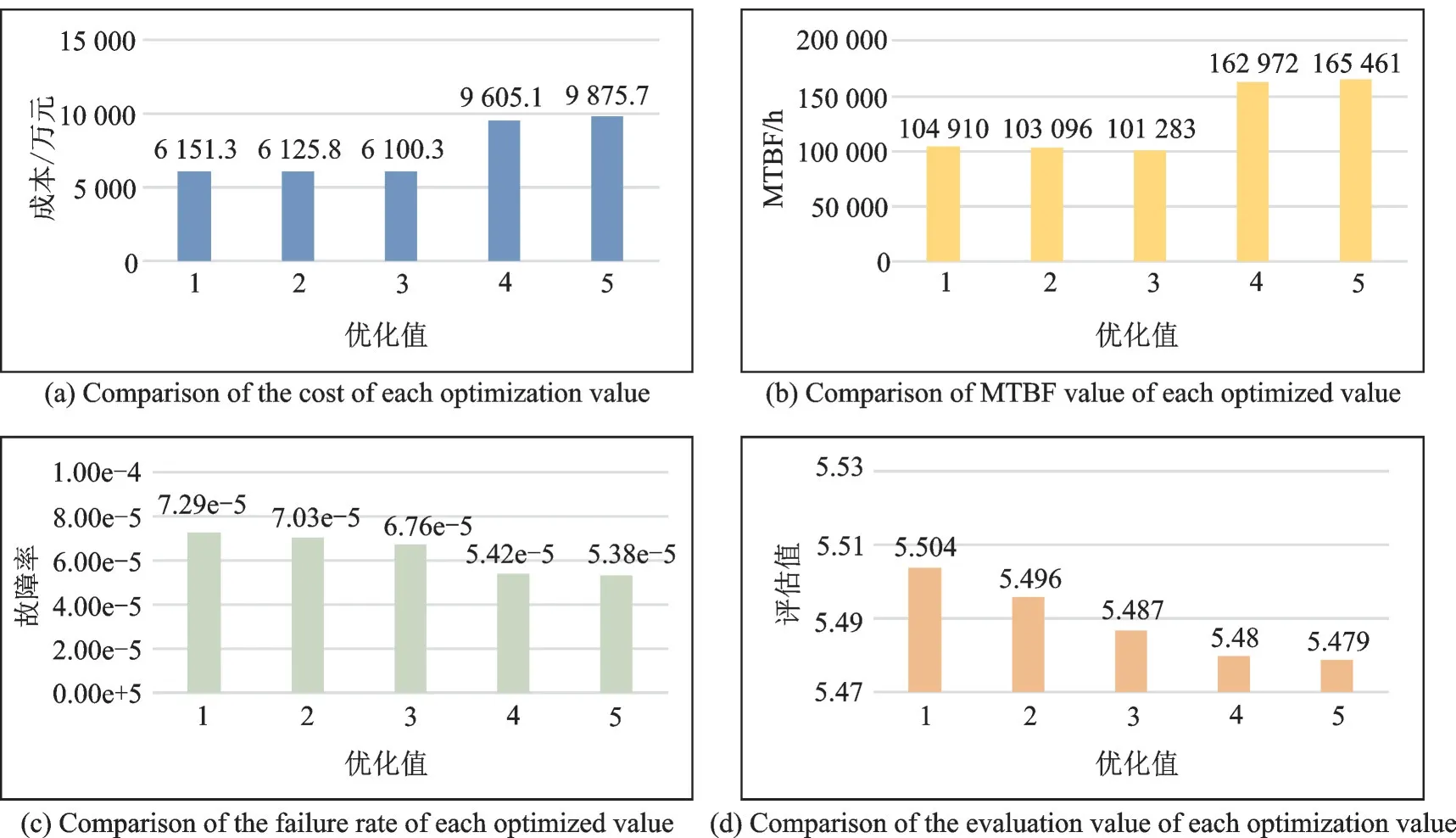
图2 多目标寻优结果对比Fig.2 Comparison of multi⁃objective optimization results

对以上的优化结果进行趋势对比，可根据不同的要求进行设计目标的确定，若系统的研发经费比较充裕，在系统可靠性、安全性方面可以做出一定的提升，则可将次优值4、5 及周围权衡域作为设计目标。如果研发经费比较紧张，可将次优值1、2、3及周围权衡域作为设计目标，但系统可靠性、安全性方面牺牲较大。

由于权重值β可以调整，故模型的灵活性较好，分别令β1=1.1、β2=0.9、β3=0.9，得到侧重成本的评估模型，作以对照

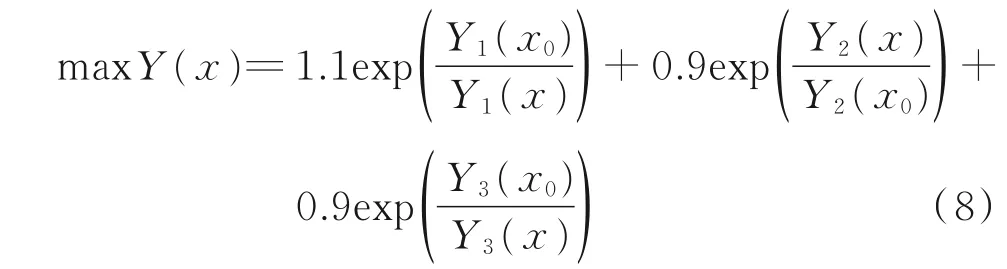
由该模型进行寻优得到表9 的寻优结果，明显可见，由于对研制成本的侧重，无量纲评估值靠前的各优化值成本均靠近单目标寻优的最优值6 023.8 万元，且MTBF 值与故障率值均非常接近，故处于同一权衡域中，决策者可以根据实际需要进行选择与参考。该结果同时说明，随着决策者在民用客机通信系统在研制不同阶段的侧重点不同，模型应当更改相应的权重以适应要求，例如本例中通信系统构型基本处于成熟阶段，安全性、可靠性量化指标趋于稳定，此时更低研制成本的方案将更受青睐。

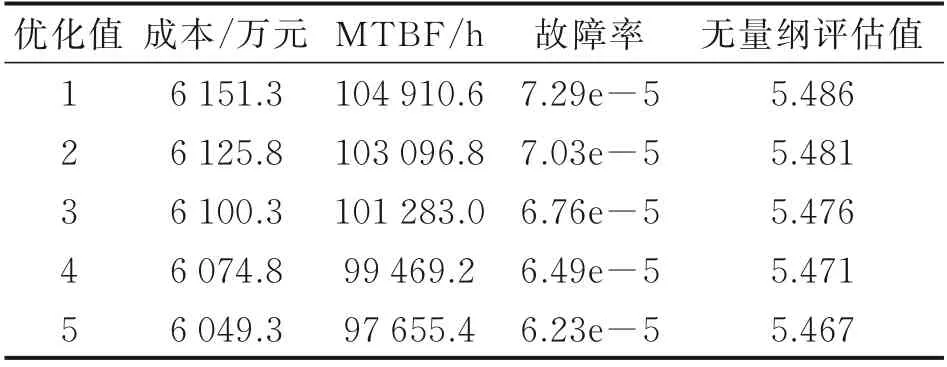
表9 侧重成本的多目标寻优结果Table 9 Multi‑objective optimization results focusing on cost

3.3 基于核和灰度的灰色马尔科夫预测模型

灰色预测就是通过原始数据的分析处理以及对灰色模型的建立，找寻系统的客观发展规律，而后对既含有已知信息，又含有未知不确定信息的系统进行预测。灰色GM（n,h）模型是灰色系统理论的基本模型，GM 表示灰色模型，n表示微分方程的阶数，h表示系统包含的变量个数。GM（n,h）模型是以变量的时间序列为基础，以微积分方程拟合而建立的模型。在对研发成本进行预测的各类方法中，较常用的灰色预测模型是GM（1,1）模型，即指考虑单个变量的灰色预测模型。

对于不同的机型不同适配的航电系统，机载通信系统的成本具有很强的不确定性，由于公开的详细系统成本数据极少且不准确，本文运用基于核和灰度的灰色预测模型，将原始序列定位为随机波动较大的区间数，同时为降低原始序列波动性以及趋势不确定性，引入马尔科夫预测模型进行修正[20⁃22]。

在灰色预测GM（1,1）中，原始数据设为按照投入市场时间排列的某系列客机通信系统研制成本范围原始数据序列，根据航空市场相关信息，将该模型的论域设定为η∈[5 500,13 500]，论域λ（η）范围为8 000 万美元根据上述定义与表10，首先得到8 种通信系统构型按投入市场时间排列后的成本范围X(⊗)，其核序列为

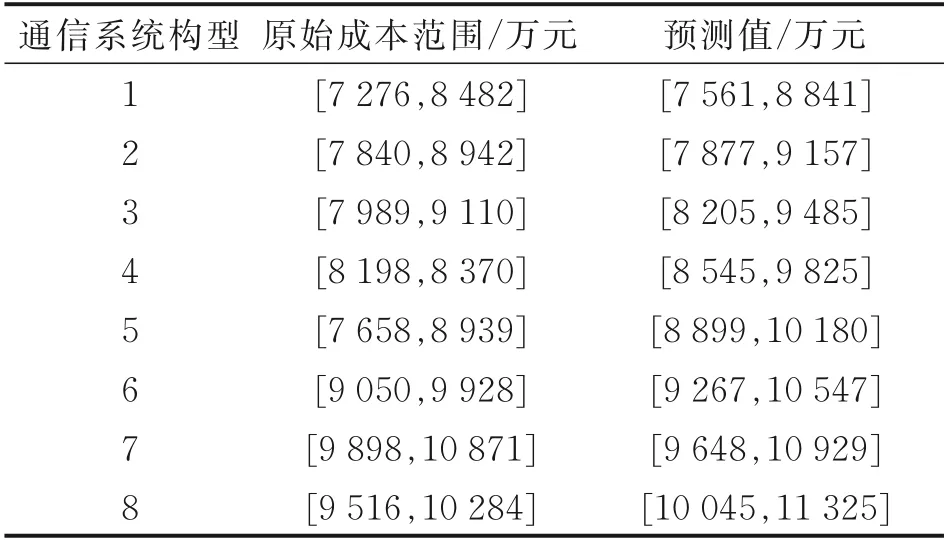
表10 8 种通信系统构型的原始成本范围与预测值Table 10 Original cost range and forecast value of eight communication system configurations

根据上文灰度计算方法与灰度不减原理：多不同灰度的区间灰数做基本运算时，运算结果灰度大于等于原始序列灰度中最大的灰度值；X(⊗)的灰度序列为

则区间灰数预测值的灰度为序列最大值0.16。

最后通过式（16）计算预测范围的核与实际核的误差率，并求平均误差率

预测平均误差率超过5%，证明马尔科夫预测模型修正的必要性。基于核和灰度的GM（1,1）预测模型结果为一条整体较为平滑的曲线，可以反映大体趋势，但对于实际情况中波动起伏大的区间序列，拟合度与精确度是较低的，对于民用客机的通信系统研制工作，由于未来新技术、新工艺的运用，有可能出现保证安全性、可靠性的同时降低成本的情况，这种情况下基于核的GM（1,1）预测模型结果的单一趋势将导致很大的误差，故采用无后效性的马尔科夫模型进行修正，减弱前列数据的影响，平衡数据随机起伏的局限性。

首先结合表10 中的实际成本范围与灰色预测成本范围，划分以下的3 种状态。

状态1：误差比例为[-5%，0%)，预测结果偏低，出现频数为1；

状态2：误差比例为[0%，5%)，预测结果偏高，出现频数为4；

状态3：误差比例为[5%，15%)，预测结果过高，出现频数为3。

上述各状态对应的结果如表11 所示，并由此得到初始状态概率转移矩阵，如表12 所示。

表11 8 种通信系统构型核预测误差比例与状态Table 11 Core prediction error ratio and status of eight communication system configurations

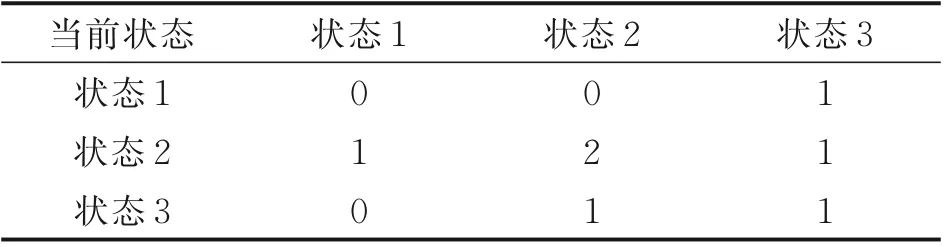
表12 初始状态转移矩阵Table 12 Initial state transition matrix

初始转移概率矩阵为

根据马尔科夫预测原理，首先由得到对该系列机型的通信系统研制成本的预测状态向量与预测区间值，状态概率向量由上代机型成本所处状态决定，例如机型8 为状态3，对应机型9 的转移矩阵中的向量为[0.125,0.5,0.375]，即转换为状态2 的概率最高；机型10 的转移矩阵由机型9 与原始状态转移矩阵决定，以此类推得到表13 状态概率值。

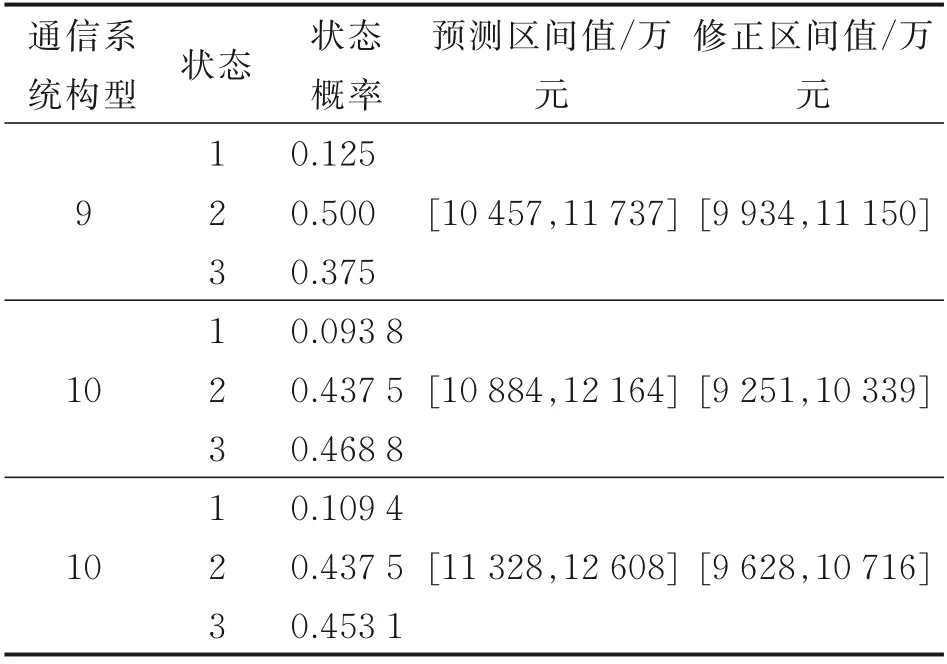
表13 预测区间与修正区间Table 13 Prediction interval and modified interval

根据得到的状态转移概率，结合设定的不同状态的误差幅值，在基于核的灰色预测区间结果上进行误差修正，如机型9 处于状态2 的概率最高，对应的误差幅值为0%～5%，则将预测区间按此幅值下调修正，具体取值可根据实际情况进行调整，本文采用最高幅值，得到的系统研制成本修正区间值。

由3.2 节得到表8 与图2 中的结果可得，该系列民用客机通信系统研制成本的权衡结果中优化值4 与优化值5 研制成本值分别为9 605 万元与9 875/万元，对应表13 中的各个预测结果，以区间的核计算误差分别为13.93%、18.31%、22.87%、平均误差为18.37%，以修正区间的核计算误差分别为8.23%、0.56%、4.43%，平均误差为4.4%，以及对比式（16）的误差计算结果，可证明：

(1)由3.2 节的多目标寻优模型得到的不同优化值需要与修正后的预测结果互为验证，才可证明权衡结果的可行性与可信度。

(2)以一体化寻优结果为基准，基于核和灰度的灰色预测模型预测平均误差为18.37%，将马尔科夫预测模型引入之后平均误差降低至4.4%，有效提高了预测模型的精确性与可信度。

(3)以修正的系统构型3 种预测成本为基准，对比安全性、可靠性、成本的权衡寻优结果4、5，误差率分别是8.23%、0.56%、4.43%，相较于权衡寻优结果1、2、3 的超过45%的误差率，是更加符合实际情况的，权衡寻优结果4、5 可以作为有效的工程参考。

4 结 论

本文主要研究民用客机通信系统，在基于成本的约束条件下进行可靠性安全性一体化设计，主要结论如下：

(1)对于系统共性因子筛选，提出了灰色线性回归关联分析组合算法，有效提高了灰色相关度与线性拟合度，从而提升了的系统共性因子提取有效性与可信度；

(2)提出加权指数ZETA 评分模型，进行单目标⁃多目标一体化框架搭建，该评分模型对优化结果进行无量纲值对比，具有灵活性强、可理解性强、精确度高的优点；

(3)由于机载通信系统研制成本的波动性，本文提出采用基于核和灰度的灰色马尔科夫预测模型，将预测模型误差由18.37%降低至4.4%，大幅提升了模型预测准确度。

(4)本文提出一体化权衡验证方案适用于指标动态变化过程，为机载通信系统以及其他飞机系统的综合评估提供一定的工程参考价值，目前已应用于新一代国产民用客机的设计验证阶段。

民用客机在通信系统结构、设备、性能以及软件方面做了很多的升级与革新，其总体上为系统贡献了更高的安全性与可靠性，但代价是付出更多的研制成本，就实际情况来看，如出于节省一定的成本的角度，在保证功能完整的情况下，可以牺牲一定的安全性，在设备级运用不同配套设备的组合工作模式，或运用技术创新性低，但更加成熟，安全性、可靠性更为稳定的系统，未来随着制造工艺的进步与研发环境的改善，在降低成本净值的基础上获得更高的系统安全性与可靠性是极有可能的。