亚声速外流与流体振荡器射流流场干扰研究

2021-09-16马志明黄河峡谭慧俊林正康唐学斌

南京航空航天大学学报 2021年4期

马志明，黄河峡，谭慧俊，林正康，唐学斌，蔡佳,2

（1.南京航空航天大学能源与动力学院，南京 210016；2.南京工业职业技术大学航空工程学院，南京 210023）

流体振荡器是一种在入口输入给定压力气源，在出口产生周期性振荡射流的主动流动控制装置［1］。流体振荡器形成振荡射流的机制主要有两点：一是Coanda 效应［2］，即流体的附壁效应；二是利用反馈通道形成负反馈回路，即流体附着在一侧壁面时，部分流体从出口流出，另一部分流体会沿着反馈通道流回混合腔入口处，附着在壁面的流体与壁面间会产生一个分离区［3］，在反馈通道中回流的流体作用下，使该分离区的尺度不断增加，从而迫使主流向另外一侧壁面靠近，直到附着于另一侧壁面。因此混合腔内的主流反复附着于壁面两侧，在出口处产生了周期性振荡射流［4⁃6］。流体振荡器具有无可动部件、结构简单、出口射流动量大、自激振荡、自激维持等优点，目前已应用在机翼边界层分离控制［7⁃9］、燃烧室中燃料增强混合［10］、燃气轮机叶片的气膜冷却［11］、噪声抑制［12⁃13］方面，并取得了有益效果。

基于其上述优点，吸引了众多学者对流体振荡器的流动特性进行了研究。Gaertlein［6，14］等通过实验手段，基于流体振荡器内部速度和压力的变化对振荡周期进行了相位平均，阐明了混合腔内分离区的演变过程，解释了内部振荡形成的原因。Park等［15］通过实验研究了流体振荡器入口落压比及几何结构对流体振荡器内部流动特性的影响，发现流体振荡器的振荡频率与出口射流最大扫掠角成反比，振荡频率越大，最大扫掠角越小，即振荡器出口射流扫掠范围越小；入口落压比、混合腔入口宽度越大，流体振荡器振荡频率越大；流体振荡器长度越长，振荡频率越小；此外反馈通道长度以及反馈通道宽度对振荡频率影响很小，可以忽略不计。雷晗等［16］通过二维数值仿真的方法研究了流体振荡器喉道宽度、出口二喉道宽度对其流动特性的影响，发现存在一个临界二喉道宽度值，当超过这个临界值，流体振荡器不能起振。Otto 等［17⁃18］通过实验对流体振荡器出口振荡射流与稳定射流的下游空间流场进行了对比，发现在振荡器出口下游较远距离处，振荡射流仍能够提供显著的控制效果，主要是振荡射流所产生的流向旋涡所致，说明出口振荡射流的扫掠行为对于实现有效的主动流动控制是关键的。因此，在输入同样的高压流体下，利用流体振荡器可以获得更好的控制效果。孟腾等［19］采用数值仿真的方法研究了流体振荡器的布局位置对S 形进气道流动分离中的控制效果，发现射流角度为45°时，控制效果最佳，总压恢复系数增加0.403%，总压畸变指数减少6.96%，分离区长度减少8.07%。

尽管目前流体振荡器已经在流场控制方面取得了很多的应用，但振荡射流是如何和外流，特别是和边界层之间传递动量，外流又对振荡射流有何影响尚缺乏相关的研究，而这对于揭示流体振荡器的流动控制机理具有重要作用。为此，本文针对外流和流体振荡器振荡射流相互干扰开展仿真研究。

1 研究对象及仿真方法

1.1 几何模型

为了开展研究，设计了一流体振荡器，其几何模型如图1 所示。流体振荡器主要由入口、混合腔、出口及反馈通道组成，其中Inlet 为流体振荡器入口，Throat 为喉道，喉道宽度La=2 mm；喉道下游为混合腔，混合腔入口宽度Lb=3.2 mm，长度Lg=13.1 mm，壁面扩张角β=77.5°；混合腔下游为二喉道，宽度为Lc=3.1 mm；流体振荡器出口的宽度Ld=10 mm，出口壁面扩张角β=60°。混合腔两侧的流道为反馈通道，反馈通道宽度Le=1.6 mm，长度Lf=16.5 mm，流体振荡器长度Lh=28.3 mm，厚度b=2 mm，出口当量直径D=10/3 mm。

图1 流体振荡器几何模型Fig.1 Geometric model of fluidic oscillator

1.2 计算方法介绍

本文采用ANSYS ICEM 软件对计算域进行网格划分，并采用结构化网格对计算域进行离散，在近壁区域及射流与外流耦合区域进行网格加密，计算区域及网格示意图如图2 所示，网格数量在350 万个左右。选用Fluent 软件进行三维流场计算，通过求解雷诺平均Navier⁃Stokes 方程模拟真实流场，选用k⁃ωSST（Shear stress transport）模型作为湍流模型，采用二阶精度的迎风格式对流动控制方程进行离散，假定流体为定比热的理想气体，分子黏性系数采用Sutherland 公式给定。采用二阶隐式的非定常进行计算，时间步长设置为1×10-6s。边界条件的设置包括：压力远场、压力入口、压力出口和无滑移绝热壁面，其中压力远场的来流马赫数分别为0、0.2、0.4、0.6、0.8，流体振荡器入口采用压力进口边界，其总压按落压比（Nozzle pressure ratio，NPR）为1.5、3 设定。

图2 计算区域及网格示意图Fig.2 Schematic diagram of calculation area and grid

1.3 算例验证

为了验证上述仿真方法的准确性，采用该仿真方法对文献［15］中的流体振荡器模型（图3）开展了不同NPR 的仿真计算，并将仿真与实验结果进行对比。仿真及实验的流体振荡器频率由图4 给出，其中Simulation 为本文仿真结果，Kulite sensor 为用压力传感器测得的实验结果。从图4 可见仿真结果与实验结果吻合较好，说明本文采用仿真方法可以准确地模拟流体振荡器的非定常射流特性。

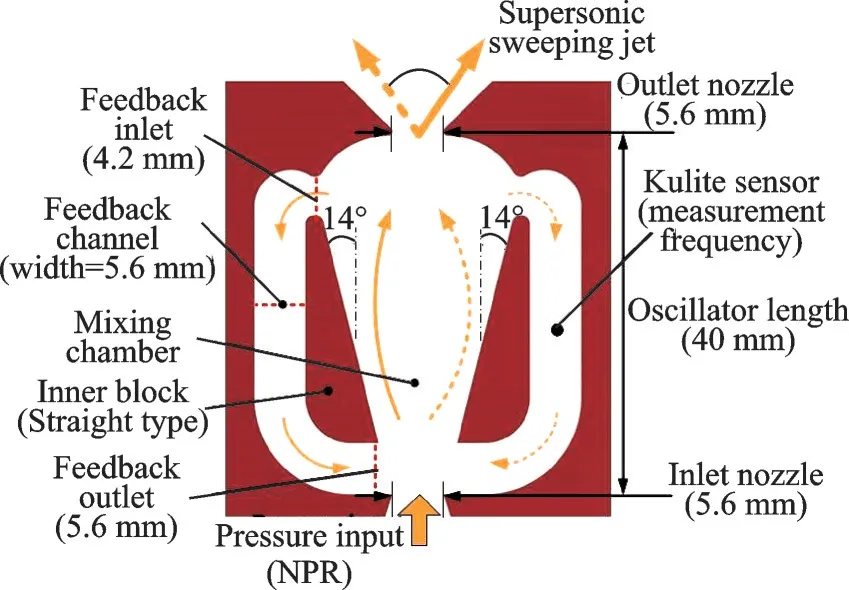
图3 参考文献[15]中流体振荡器构型及几何参数Fig.3 Configuration and geometric parameters of fluidic os⁃cillator in Ref.[15]

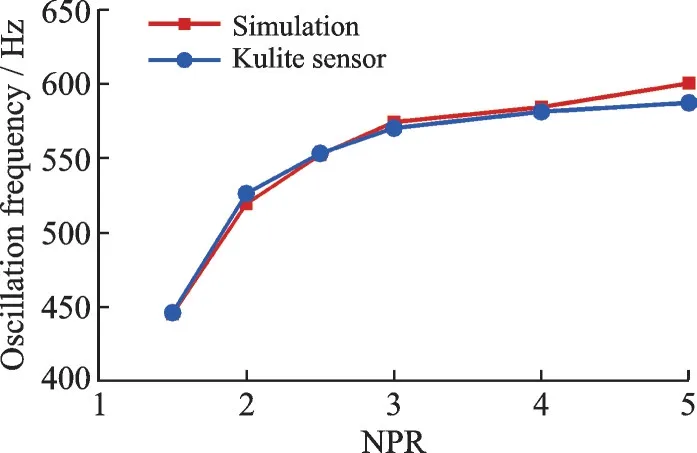
图4 不同落压比下流体振荡器的振荡频率Fig.4 Oscillation frequency of fluidic oscillator at NPR

2 仿真结果分析

2.1 外流对流体振荡器的内部流动特性的影响

为了评估外流是否会对振荡器内部流场产生影响，通过快速傅里叶变换对比了落压比NPR=1.5、3 时不同外流马赫数下流体振荡器出口速度在z方向的分速度Uz的频谱特性，表1 给出了不同外流马赫数下入口落压比NPR=1.5、3 时流体振荡器的振荡频率。由表1 可知，当入口落压比NPR=1.5，外部为静止外流时（Ma=0），流体振荡器的振荡频率为1 515 Hz。随着外流马赫数的增加，射流的振荡频率从1 515 增加至1 650 Hz，这说明来自外流的扰动会影响流体振荡器的振荡频率。图5给出了落压比NPR=1.5 时不同外流马赫数下的流体振荡器内部时均马赫数云图，其中时均流场通过对10 个周期的流场进行时间平均处理得到。由于积分的时间很长，振荡器左右振荡效应被抹平，其时均流场呈现出很好的左右对称特性，可以看到出口二喉道处均为亚声速，不能隔离外流扰动，这可能是因为外流马赫数增加之后，外流对射流的束缚作用增强，使得从二喉道流出的流量减少，更多的流体流入反馈通道，从而反馈通道内的气流流速增加，振荡器的振荡频率逐渐增大。当入口落压比NPR=3，Ma=0、0.2、0.4、0.6、0.8 时，射流的振荡频率均为2 500 Hz。频率增大的原因是，入口落压比越大，如图5、6 所示，振荡器内流体过膨胀程度削弱，气流的流速越大，振荡器流场时均马赫数由0.045 增加到0.11，气流在混合腔的两侧壁面之间来回振荡的时间减小，从而振荡频率增大。为了解释频率保持不变的原因，图6 给出了NPR=3 时不同外流马赫数下的流体振荡器内部时均马赫数云图，图中用黑色实线标注出了声速线，可以看到出口二喉道处均达到临界状态，在二喉道下游存在一个小范围的超声速区。因此，NPR=3 状态下，二喉道处声速截面的存在可以隔离外流扰动，使得流体振荡器的内部流动特性不受外流的影响。

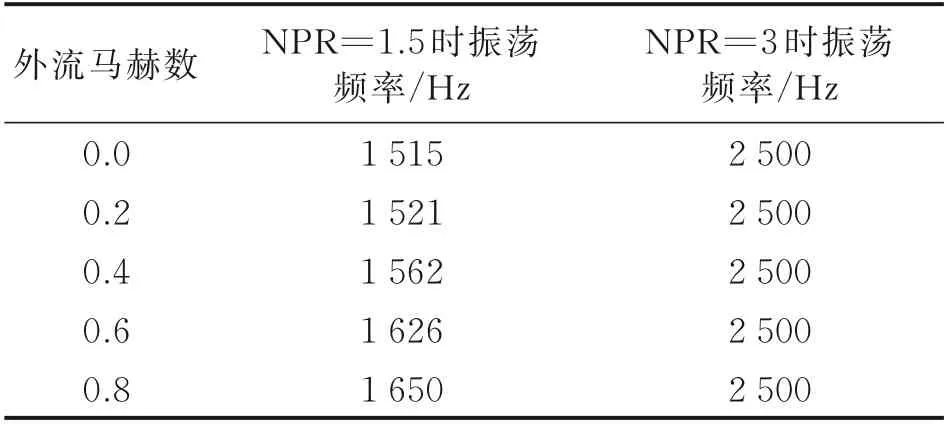
表1 不同外流马赫数下入口落压比为1.5、3 时流体振荡器振荡频率Table 1 Oscillation frequency of fluidic oscillator at dif⁃ferent crossflow Ma when NPR = 1.5，3

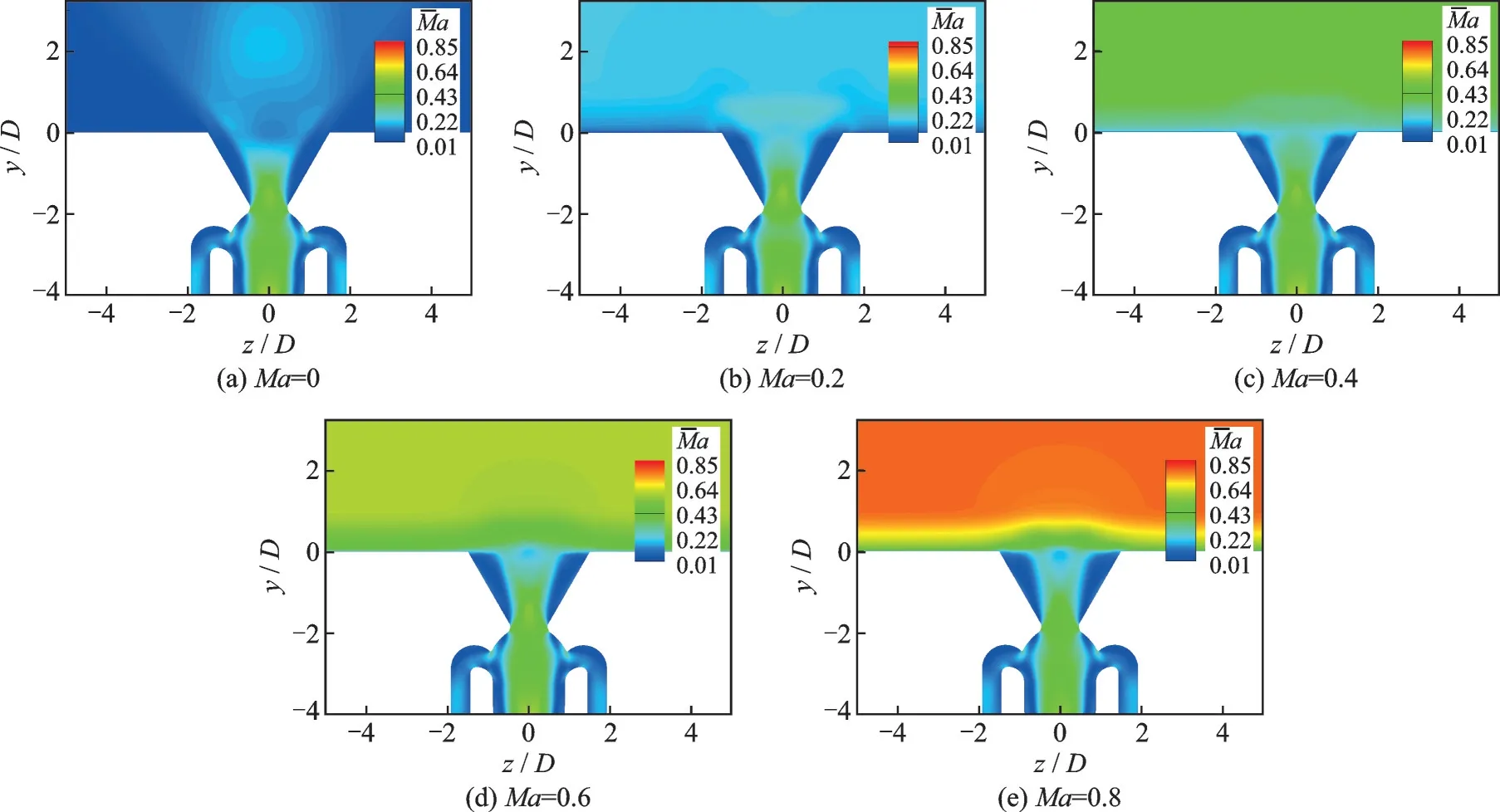
图5 NPR=1.5 时不同外部来流马赫数下的流体振荡器时均马赫数云图Fig.5 Time averaged Ma cloud diagram of fluidic oscillator at different crossflow Ma when NPR = 1.5

图6 入口落压比NPR=3 时不同外部来流马赫数下的流体振荡器时均马赫数云图Fig.6 Time averaged Ma cloud diagram of fluidic oscillator at different crossflow Ma when NPR = 3

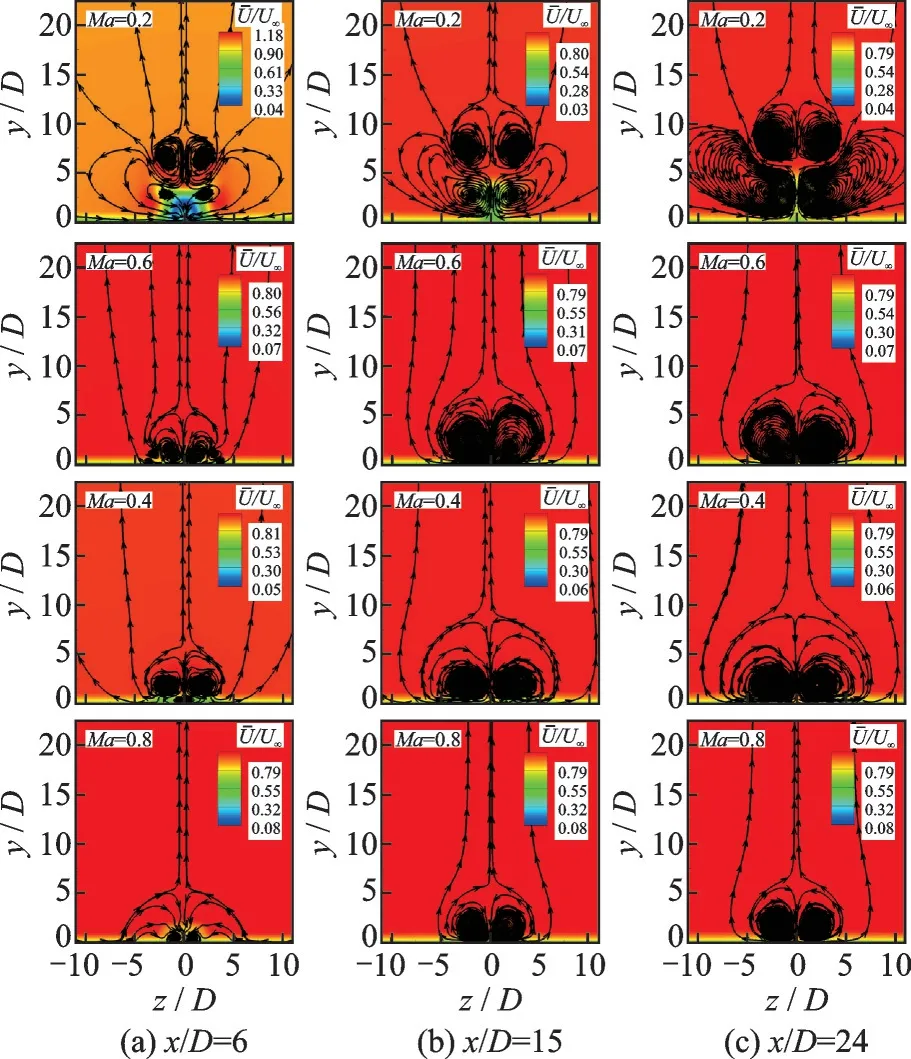
图7 入口落压比NPR=3 时不同外流马赫数下沿流向截面的时均流线图Fig.7 Time averaged streamline along the flow section at different crossflow Ma when NPR = 3

2.2 NPR=3 时外流干扰下流体振荡器出口振荡射流空间流场结构

一外流马赫数下，射流诱导的流向旋涡的涡核位置沿流向截面逐渐远离壁面和截面中心线。随着外流马赫数越小，同一流向截面位置流向旋涡的涡核位置越远离壁面和截面中心线，说明射流的穿透深度和射流影响域都在增加。射流，射流剪切层内存在一系列Kelvin⁃Helmhotz旋涡；当外流马赫数增加之后，旋涡随外流向下游对流，上方的旋涡会由圆环状逐渐转变为尖头状。

表2 NPR=3 时不同外流马赫数下右侧流向旋涡涡核位置Table 2 Position of right vortex core in flow direction at different crossflow Ma when NPR = 3

图8 入口落压比NPR=3 时不同外流马赫数下流场三维旋涡结构Fig.8 Three dimensional vortex structure of flow field at different crossflow Ma when NPR = 3

图9 给出了振荡射流在z/D=0 截面处的速度流线图对比，其中Uy为时均速度在y方向上的分速度；可以看出，外流Ma=0 时流体振荡器出口射流的流线是直直地向上；来流Ma=0.2 时，射流受外流压迫向下弯曲，由于外流速度较低，射流的弯曲程度较小，射流下游存在一个大的回流区，之后射流始终脱离壁面，如图9（c）所示；当来流Ma=0.4 时，射流在下游快速贴近壁面，射流下游回流区较小；当外流马赫数进一步增加时，射流来流Ma=0.6 和Ma=0.8 的射流非常贴近壁面，几乎没有回流。表3 给出了NPR=3 时不同外流马赫数下射流最大穿透深度，可知在NPR=3 时，外流马赫数越大，射流的最大穿透深度越小。

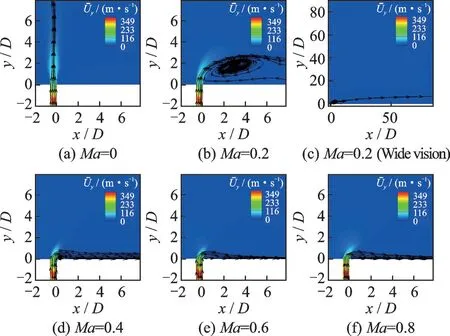
图9 射流在z/D=0 截面处的流线图对比Fig.9 Comparison of streamline diagram of jet at section z/D = 0

表3 NPR=3 时不同外流马赫数下射流最大穿透深度Table 3 Maximum penetration depth of jet at different crossflow Ma when NPR = 3

为了分析外流马赫数对射流流场内流结构的影响，表4 列出了不同外流马赫数状态下对应的动量比。动量比的计算公式为

表4 NPR=3 时不同外流马赫数下射流与外流动量比Table 4 Jet to crossflow momentum ratio at different crossflow Ma when NPR = 3

式中：ρ、U分别为密度和速度，下标jet 代表射流，下标∞代表外流。射流的出口动量通过时间积分得到，可以看到，当外流马赫数为0 时，动量比为无穷大，外流马赫数为0.2 时，动量比为2.21。随着外流马赫数的增加，外流本身的动量随之增加。根据前面的分析，外流对振荡器内部流场没有影响，射流的出口动量不随外流的改变而改变，射流和外流的动量比呈现出逐渐降低的趋势，并且当外流马赫数超过0.4 之后，射流与外流动量比小于1。故当外流马赫数为0.2 时，由于此时射流的动量较外流动量高得多，射流的穿透深度大，射流形成气柱诱导外流边界层分离，卷起马蹄涡；当外流马赫数增加之后，外流对射流的束缚能力增强，射流穿透能力很弱，形成的气柱很难诱导外流边界层分离，因此在流场中无法观测到马蹄涡的存在，射流流场以流向涡对占据主导。

2.3 NPR=3 时外流对射流时均速度场的影响

边界层内的速度分布直接决定了边界层抵抗下游逆压梯度的能力，为此，图10 给出了不同外流马赫数下，沿流向截面x/D=6、15、24 处的时均速度比（速度比=当地时均流速/外流流速）图。从图中可以看出，在Ma=0.2 时，x/D=6 截面处，在中心处存在一低速环形区域，实际上该区域对应于射流所形成的马蹄涡；在x/D=15、24 截面处，随着旋涡进一步向上方运动并和外流形成较强的流动掺混，低速区内的速度随之增高。当外流马赫数Ma增加至0.4 时，会形成中心处高、两端低的速度比云图，随着向下游发展，中心处的低能流会逐渐减少，这是因为一对左边顺时针，右边逆时针的流向旋涡会将中心处的低能流逐渐排移到两侧。Ma=0.6、0.8 时的速度比云图和Ma=0.4 时的大致相同。

图10 不同外流马赫数下沿流向截面的时均速度比Fig.10 Time average velocity ratio along the flow section at different crossflow Ma

图11 进一步定量对比了x/D=24 截面z/D=0、3、9、15 位置的速度剖面，其中纵坐标为距离壁面的高度，横坐标为当地流速与来流流速的比值，z/D=15 位置远离射流影响区，可作为未受扰动区的基准。表5 给出了不同外流马赫数下沿流向x/D=24 截面不同展向位置速度剖面的形状因子H1，其中H1为流量损失厚度与动量损失厚度的比值。当Ma=0.2 时，z/D=0、3、9、15 位置的形状因子分别为1.384、1.175、1.301、1.331，结合图11（a）可知，在z/D=0 处的速度剖面较z/D=15 位置更加削瘦，在z/D=3、9 处的速度剖面比z/D=15 处的更加饱满。结合图7 可以发现，这种速度剖面分布主要是由于马蹄涡的存在导致的。当外流Ma=0.4、0.6、0.8 时，z/D=0 处的速度剖面，特别是非常靠近壁面位置，较z/D=15 更为饱满，但会使得速度边界层增厚，这是由于上方流向旋涡速度较低所导致的；z/D=9 处的速度剖面与z/D=15处基本一致，说明Ma=0.4、0.6、0.8时振荡射流的影响区域相较于Ma=0 更小。当外流Ma=0.4、0.6、0.8时，z/D=0、3、9位置的形状因子相较于各个状态z/D=15 位置的形状因子逐渐增大，这说明射流与外流所诱导的流向旋涡可以提高抗分离能力。

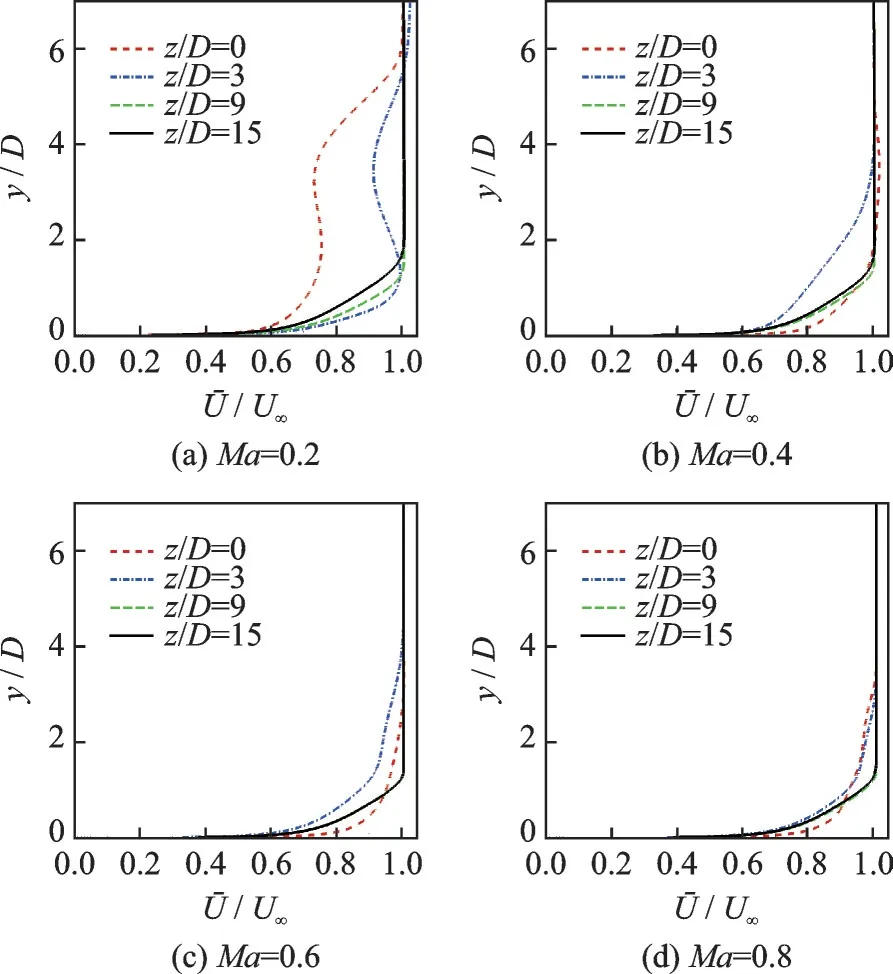
图11 沿流向x/D=24 截面位置速度剖面Fig.11 Velocity profile along the flow direction at section x/D = 24

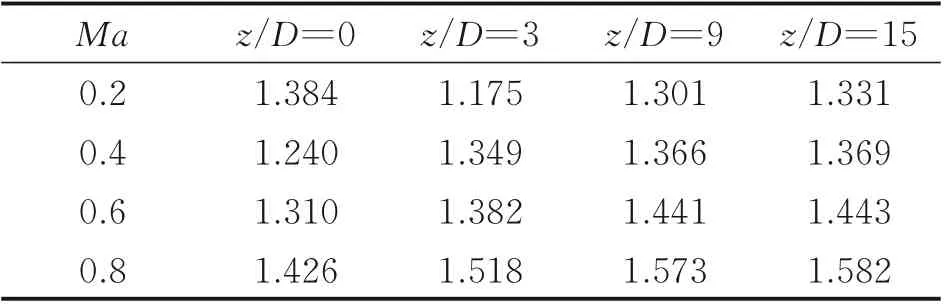
表5 不同外流马赫数下沿流向x/D=24 截面不同展向位置速度剖面的形状因子H1Table 5 Shape factor H1 of velocity profiles at different spanwise positions along the section with flow direction x/D = 24