姿态传感器的坐站转移测量系统研究
2021-09-14陈宝亮肖飞云
刘 鹏,陈宝亮,肖飞云,王 勇
(合肥工业大学 机械工程学院,合肥 230009)
坐站转移运动是人类最基本的功能性活动,是人类独立进行日常生活活动的基本前提[1-2],从生物力学的角度来看,坐站转移运动需要不同肌肉之间的相互协调,以及需要足够的肌肉力量提升身体重心运动;对于脑卒中偏瘫患者而言,坐站转移能力是决定其能否独立生活的重要功能基础[3]。因此,对于坐站转移能力的评估显得尤为重要。在临床上,关节力矩是评估坐站转移能力的常用指标[4],在康复训练器材的设计上,关节力矩对于驱动器的选择具有重要意义。近年来一些学者也开始了坐站转移运动辅助训练器材的研究[5-7],然而,建立一个有效的人类日常活动的动力学模型是设计残疾人辅助装置的关键步骤[8]。因此,分析人体坐站转移运动对于康复评估和康复训练器材的设计显得至关重要。
在人体生物力学的研究中,三维运动捕捉系统通常被认为是人体运动分析的黄金标准,Pinheiro C等[9]通过运动捕捉系统和测力板对人体坐站转移进行了运动学和动力学分析;Yoshioka S等[10]通过运动捕捉系统对人体坐站转移的运动学和关节最小峰值力矩进行了研究;Shia V等[11]研究了基于摄像系统的坐站转移的事件检测,然而基于摄像机的运动捕捉系统虽然测量精度高,但是价格昂贵,测量环境要求高,只能在特定的实验室内进行。近年来,传感器技术的进步使小型和低成本的可穿戴设备得以迅速发展,这些设备具有复杂的功能来监测人体的运动。例如,李元良等[12]研究了一种基于MEMS(micro-electro-mechanical system)传感器的人体运动识别系统;Kong A等[13-15]实现了基于三轴加速度传感器的人体跌倒的检测;刘坤等[16]通过可穿戴传感器和测力板分析了人体坐站转移的动力学特性,并与运动捕捉系统进行比较,然而其传感器必须安装在人体体段的质心位置,难以实现实际安装。目前,基于姿态传感器来分析人体运动的相关研究较少,姿态传感器能够精确测量载体的姿态角,其内部包含了三轴陀螺仪、三轴加速度计、地磁场传感器,采用高性能的微处理器和先进的动力学解算与卡尔曼动态滤波算法,能够快速求解出模块当前的实时运动姿态,这对于人体运动分析提供了便利。
通过以上文献分析,在人体坐站转移的运动研究中,现有方法大都采用运动捕捉系统采集人体的关节角度信息。基于摄像机的运动捕捉系统价格昂贵,反射标记的安装耗时长,对于安装位置要求较高,而且容易被遮挡,同时需要专用的实验室空间,后处理(包括反射标记的识别、跟踪、空间坐标的计算)时间长,不适合作为一种临床的技术手段。
因此,为解决上述技术问题,基于多个姿态传感器解算人体在坐站转移运动过程中踝关节、膝关节和髋关节的运动角度,通过建立简化的人体动力学模型,将理论计算得到的足底压力信息与测力板测得的实际数据进行了对比,验证基于姿态传感器的坐站转移测量系统的准确性与有效性,并利用拉格朗日方法对坐站转移运动进行动力学分析。
1 运动学信息采集及动力学建模
1.1 运动模型的建立及参数获取
对人体坐站转移的运动进行分析,首先需要将人体简化为适当的计算模型,再运用坐标变换的数学方法解决人体运动位姿的计算[17]。本文研究人体坐站转移的运动学信息,不考虑上肢和头部姿态,所以将头部、上肢和躯干简化为一根连杆,假设人体坐站转移的运动是关于矢状面对称的且只在矢状面内运动[18],足部始终与地面接触且不发生相对运动,把左右小腿和大腿均用连杆表示,故将人体简化为三连杆模型,三连杆之间通过转动副连接。
简化的人体三连杆刚体模型如图1所示,按照右手定则,定义姿态传感器的惯性坐标系W,在足部建立全局坐标系{OXYZ},坐标原点O位于踝关节处,规定Y轴垂直于地面向上,X轴水平向前,在小腿、大腿和躯干分别建立局部坐标系{oixiyizi},i=1,2,3,坐标原点分别位于踝关节、膝关节和髋关节处,如图1中所示,yi由关节i指向关节i+1,xi垂直于yi向前,规定关节角度θi为yi与X正方向的夹角;其中关节角度θi通过如下方法计算:
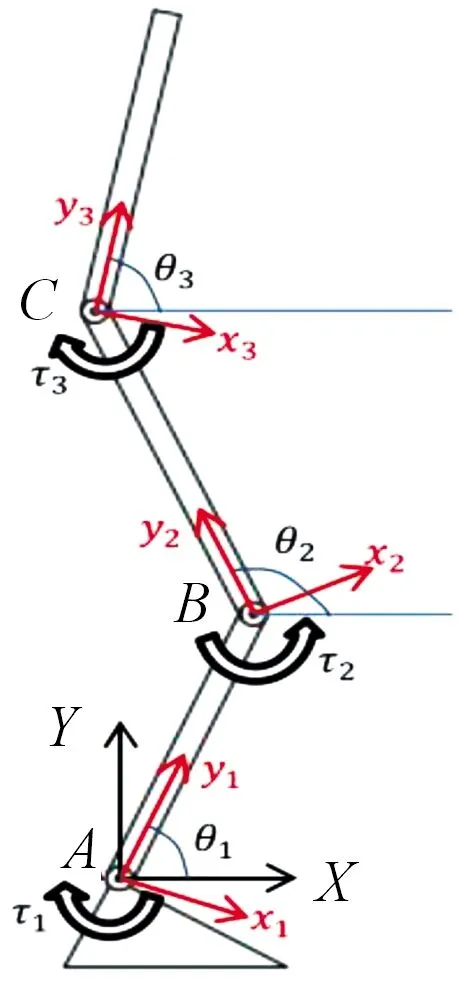
图1 人体三连杆刚体模型示意图
设小腿、大腿和躯干的长度分别为l1、l2和l3,关节回转中心分别为A、B、C,对于踝关节角度θ1,膝关节中心B在坐标系{o1x1y1z1}下的位置矢量为:
(1)
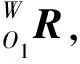
(2)
则膝关节中心B在坐标系{OXYZ}下的位置矢量为:
(3)
A点到B点的方向向量记为a,故a为:
(4)
因此,向量a与X轴正方向的夹角即踝关节角度为:
(5)
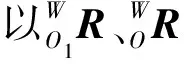
(6)
因此:
θ1=cos-1(ox)
(7)
同理,θ2、θ3可由同样的方法得到。
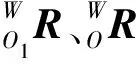
该姿态传感器在用欧拉角表示姿态时的坐标系旋转顺序为z-y-x,这种描述姿态传感器上的局部坐标系{oixiyizi}的方位的法则为:局部坐标系{oixiyizi}的初始方位与惯性坐标系W相同,首先使其绕zi轴旋转γ角,然后绕yi轴旋转β角,最后绕xi轴旋转α角,其中各次旋转都是相对于运动坐标系的某轴进行的,从而得到表达式:
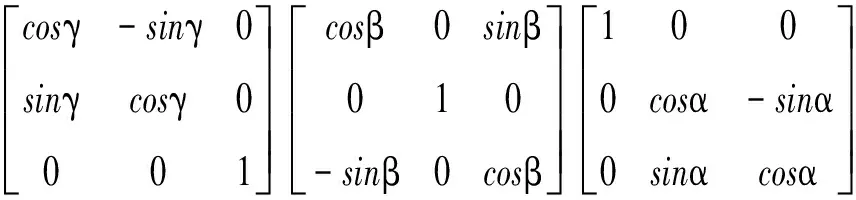
(8)
即旋转变换通式:
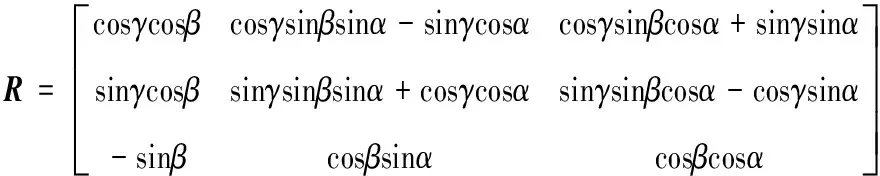
(9)
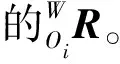
1.2 坐站转移的动力学建模
刚体动力学分析的主要方法有牛顿—欧拉方法、拉格朗日方法,牛顿—欧拉方法在运用时既要考虑外界驱动力,又要考虑产生加速度的惯性力,拉格朗日方法则基于系统能量的概念,这种方法只需速度而不必求各杆件的内作用力,直接求出关节的驱动力矩,是一种比较清晰简便的方法[20]。本研究采用拉格朗日方法进行动力学分析。
在任一时刻,连杆1的质心位置:
xc1=lc1cosθ1
(10)
yc1=lc1sinθ1
(11)
连杆2的质心位置:
xc2=l1cosθ1+lc2cosθ2
(12)
yc2=l1sinθ1+lc2sinθ2
(13)
连杆3的质心位置:
xc3=l1cosθ1+l2cosθ2+lc3cosθ3
(14)
yc3=l1sinθ1+l2sinθ2+lc3sinθ3
(15)
其中:lci(i=1,2,3)为体段i质心到其局部坐标系原点的距离。
在坐站转移过程中,当人体脱离座位后,此时只受到地面对人体的作用力,所以此时系统的势能为:
m1glc1sinθ1+m2g(l1sinθ1+lc2sinθ1)+
m3g(l1sinθ1+l2sinθ2+lc3sinθ3)
(16)
其中:mi表示刚体i的质量,g表示重力加速度。
系统的动能为:
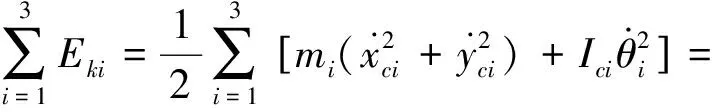
(17)
其中:Ici(i=1,2,3)表示刚体i相对于其质心的质量惯性矩。
拉格朗日函数L定义为系统的动能Ek与总势能Ep之差,即:
(18)
则系统的动力学方程为:
(19)
联立可得,脱离座位后各关节力矩:
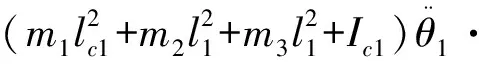
(m1lc1+m2l1+m3l1)gcosθ1
(20)
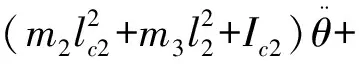
(m2lc2+m3l2)gcosθ2
(21)
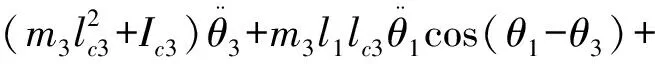
(22)
在坐站转移运动中,由于躯干所受的外力始终只有重力作用,在脱离座位前,式(22)仍然适用。
由牛顿第二定律可知,地面的支撑反力为:
Fy=(m0+m1+m2+m3)g+
(23)
2 实验及结果分析
2.1 实验
为验证前述方法的准确性与可行性,搭建了基于姿态传感器的人体坐站转移运动测量系统,通过3个姿态传感器采集人体坐站转移过程中的下肢关节角度信息。同时,利用测力踏板采集人体坐站转移运动过程中足部受到的地面反力,如图2所示。
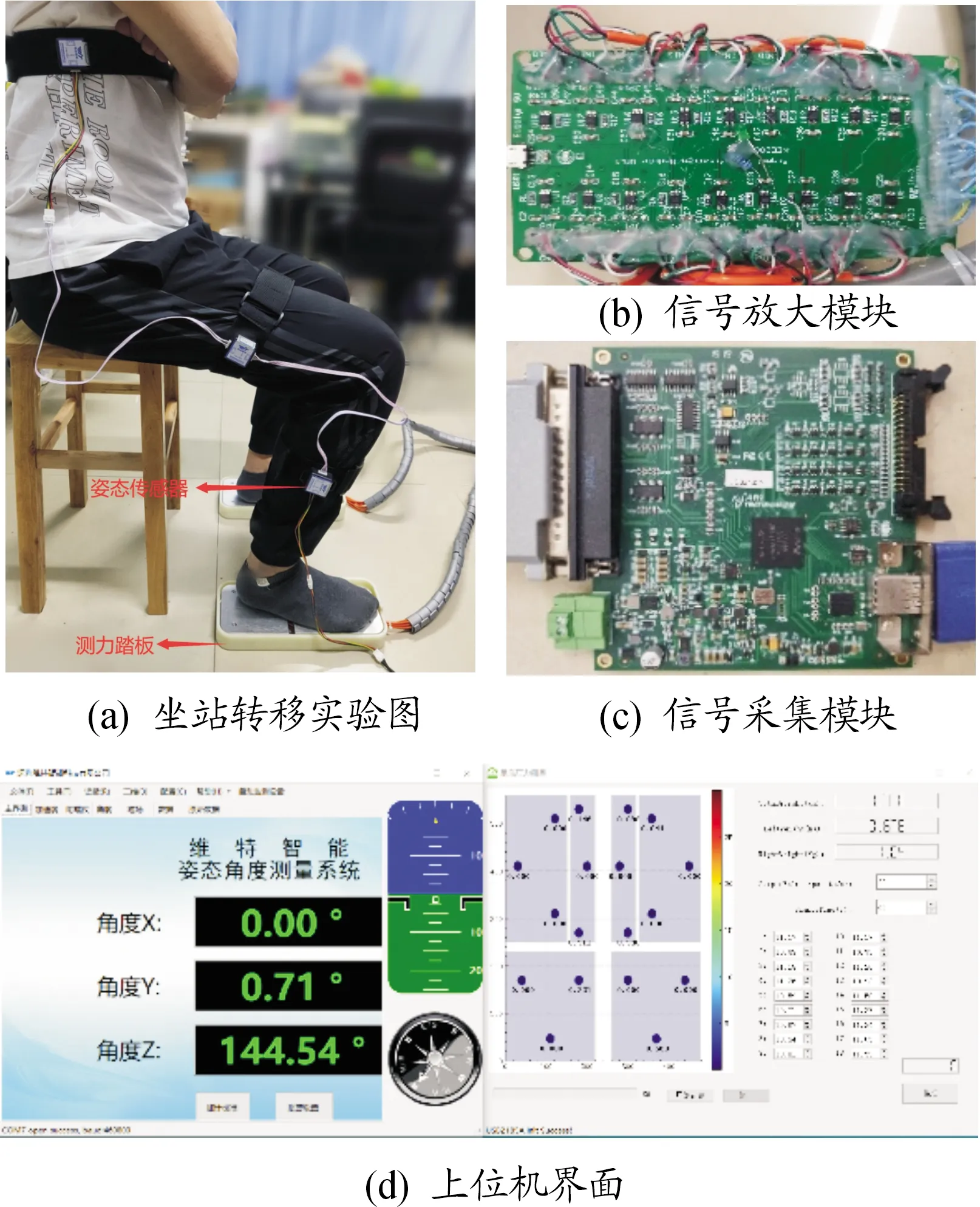
图2 坐站转移运动测量系统
采用深圳维特智能科技有限公司型号为WT 901C 485的姿态传感器,该传感器支持多个模块级联,在上位机上能够同时采集多个模块的数据,该模块内部集成了高精度的陀螺仪、加速度计、地磁场传感器,能够在动态环境下准确输出模块的当前姿态,姿态测量精度0.01°,加速度测量精度0.01g,角速度测量精度0.05(°)/s;姿态传感器通过USB直接与上位机通信,采样频率为50 Hz;测力踏板压力传感器选用蚌埠大洋传感公司型号为DYLY-108的压力传感器,量程为50 kg;该传感器的输出灵敏度为1.0~2.0 mV/V,工作电压为5.0~10.0 V;测力踏板通过信号放大模块和信号采集模块与上位机实时通信,采样频率为50 Hz。
实验招募了7名健康且没有任何运动障碍的男性在校学生,7名受测者的基本信息如表1所示。根据《GB/T 1000—1988.中国成年人人体尺寸》和《GB/T 17245—2004.成年人人体惯性参数》,受测者的各项人体测量学数据如表2所示。表2中给出了7名受测者各肢段的长度li、质量mi、质心位置lci以及关于质心的转动惯量Ici,在实验中,受测者以平时的习惯性坐姿为准,双手自然放置于膝盖上,座位高约为0.45 m,3个姿态传感器通过绑带分别固定于小腿、大腿、躯干位置,保证每个姿态传感器的y轴方向沿着所在肢段两端关节的连线,并由下端指向上端,2个测力踏板放置于受测者脚下,左右距离以个人平时习惯性坐姿为准,由于健康人群的坐站转移运动通常被认为是关于矢状面对称的[18],因此在实验中只采集身体一侧的运动数据;受测者穿戴好实验器材后,要求受试者保持稳定的站立姿势,对姿态传感器的安装误差进行校准;由于实验对象都是健康的大学生群体,因此本研究认为,在静态站立时,受测者身体与地面保持垂直,以此校准姿态传感器的安装误差。
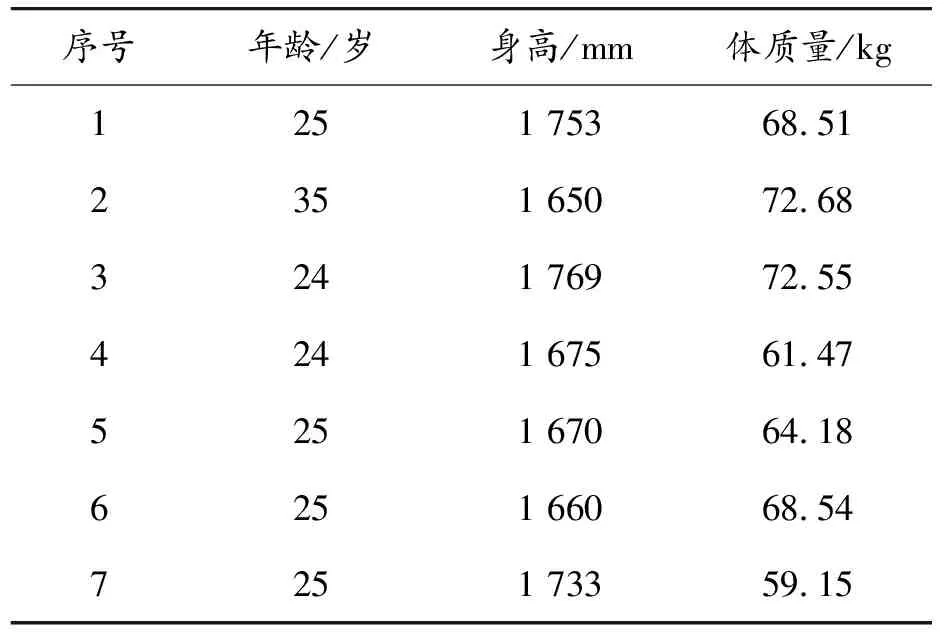
表1 7名受测者的基本信息
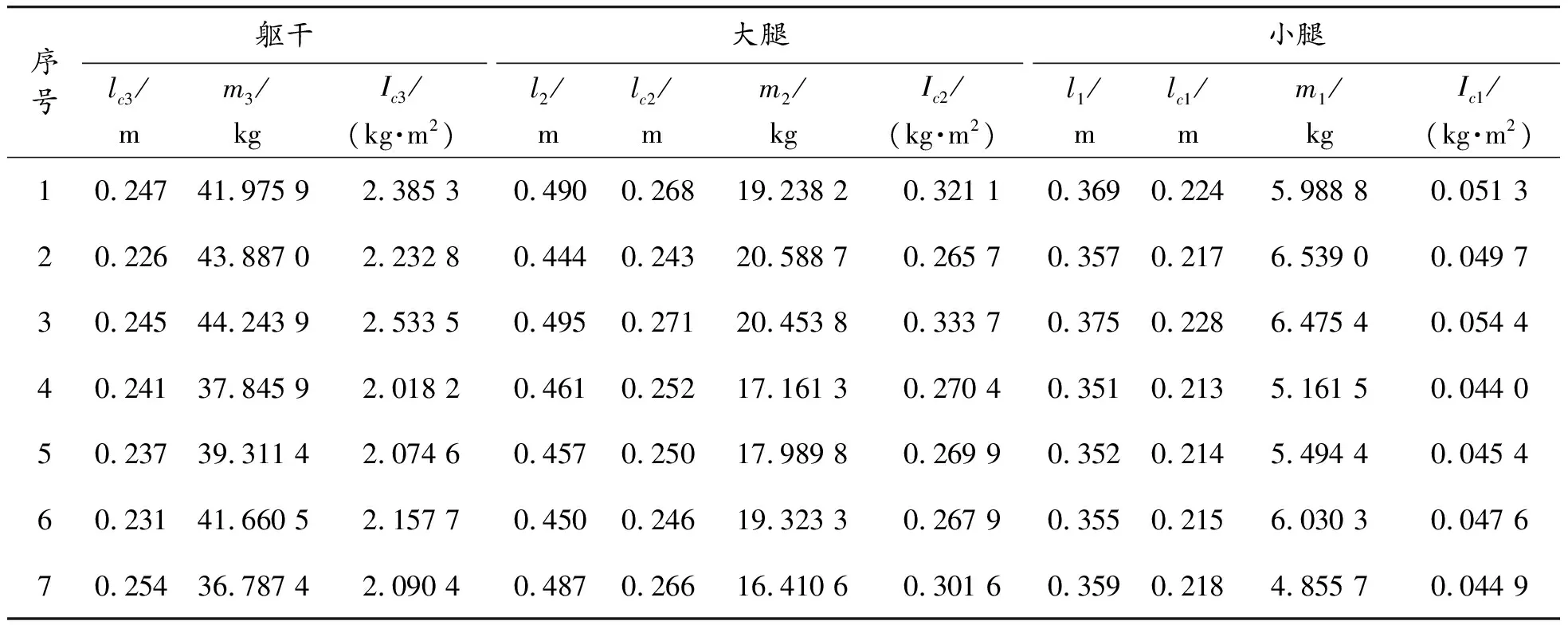
表2 7名受测者的人体测量学数据
2.2 实验结果分析
实验完成后,将受测者的坐站转移时间做归一化处理,将足底压力与受测者体重进行标准化处理;最终得到7名受测者坐站转移运动的关节角度数据和足底压力数据;其中1名受测者的坐站转移运动的关节角度曲线和足底压力曲线如图3、4所示,图中A1、B1、C1分别表示θ1、θ2、θ3在运动初始时刻的角度;A2、C2分别表示θ1、θ3在运动过程中的最大屈曲角度;A3、B3、C3分别表示θ1、θ2、θ3在运动结束时刻的角度(最大伸展角度),同理,F1、F2、F3、F4、F5分别表示运动初始时刻的压力值、运动过程中的压力峰值以及运动终止时刻的压力值;7名受测者各个时刻的角度数据和足底压力数据见表3、4。
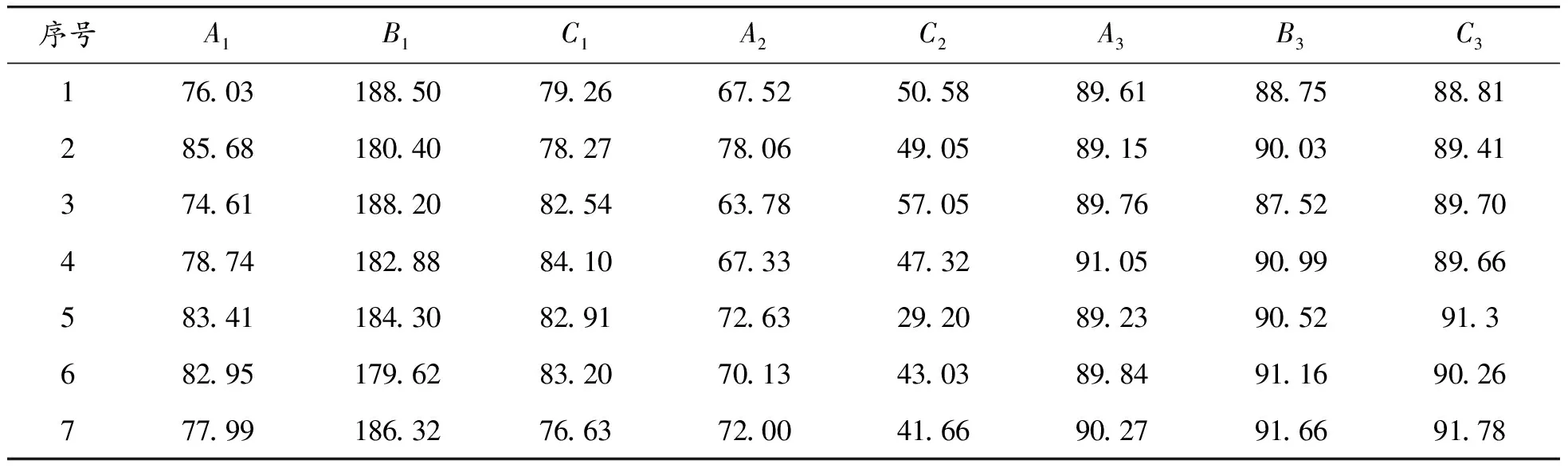
表3 7名受测者各时刻关节角度数据 (°)
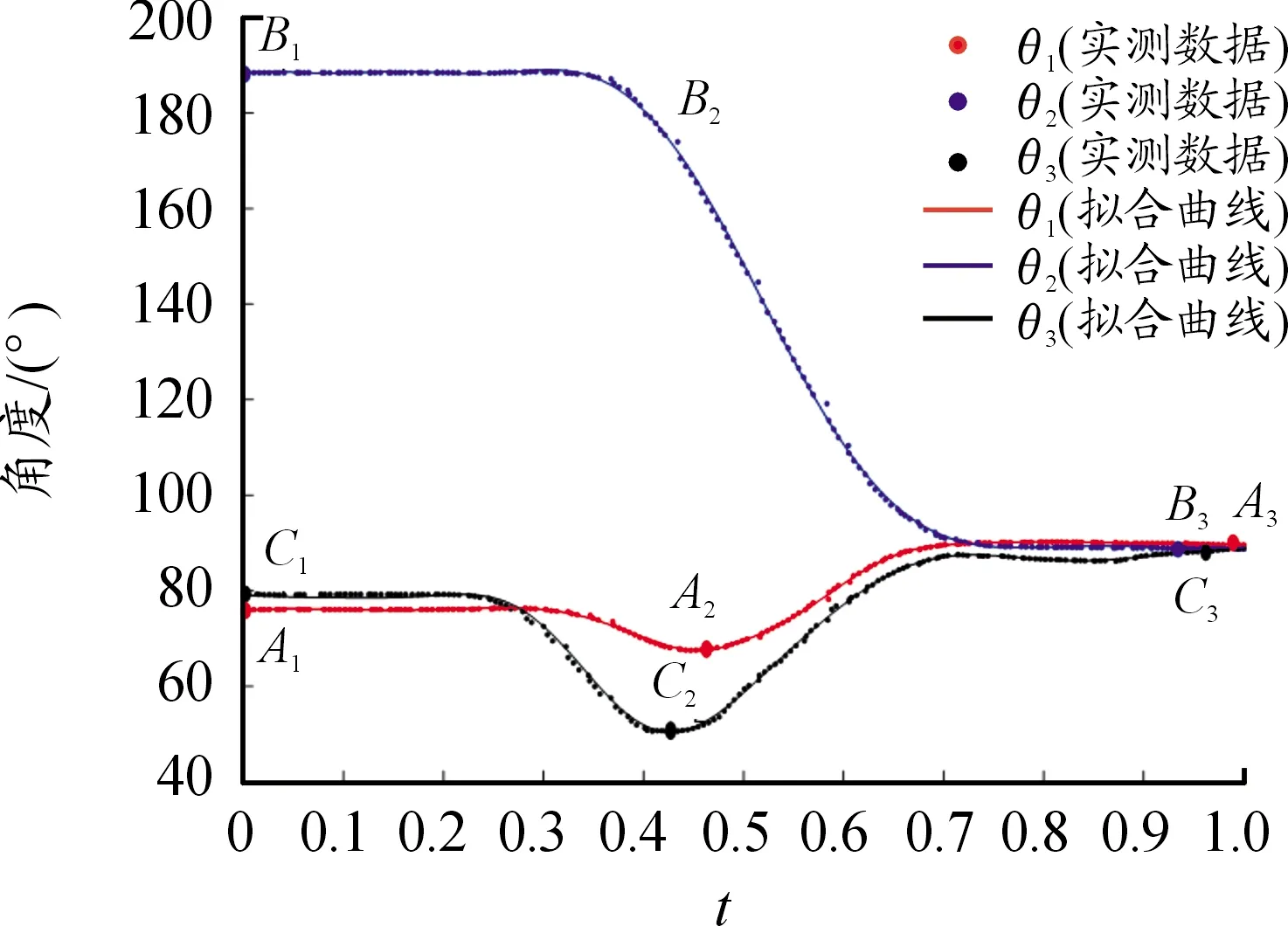
图3 1名受测者坐站转移的关节角度曲线
由图3、4可知,在坐站转移的开始阶段,此时躯干与水平面夹角大约为80°,之后髋关节角度开始变化,躯干开始前倾,此时足底压力开始减小,当足底压力到达第一个波谷后(F2),踝关节和膝关节开始运动,身体由一个稳定的坐姿状态加速上升,此时足底压力快速增大,当足底压力达到最大值后(F3),重心继续上升,足底压力开始减小,当足底压力到达第二个波谷后(F4),足底压力开始增大,身体逐渐伸直至完全站立。
为了验证姿态角解算关节角度的正确性,将关节角度数据代入式(23),从而得出足底压力的理论计算数据,由于姿态传感器放置在衣服的外侧,人体肌肉的形变和衣服的滑移,使姿态传感器相对于非刚性的人体产生微小的位姿变化,造成曲线的不圆滑,本研究对角度曲线进行了拟合,如图3所示。将拟合后的关节角度曲线数据代入式(23),进而得出足底反力的理论计算数据;在坐站转移过程中,当人体离开座位前,式(23)的计算数据不能反映足底的受力情况,因此需要确定人体离开座位的时间点。文献[21]中,当足底的支撑反力达到最大时,认为可作为离开座位的时刻。本文中以最大地面反力出现的时刻(F3)为起始点,将实际测量的地面反力数据与理论计算结果进行对比,其中1名受测者理论计算数据和实际测量数据曲线见图4,7名受测者数据见表5。表5中给出了离开座位后,足底压力的理论计算与实测数据间的均方根误差(RMSE)和相关系数(R)。从表5可以看到,通过理论计算和测力板得到的地面反力二者间具有较大的相关系数(R≥0.91),实测数据和理论计算数据有一定的误差,但误差较小(RMSE≤0.44);因此,基于姿态传感器的测量系统是可靠的,可以用于坐站转移的研究。通过分析左右测力踏板各自压力数据可以发现,在坐站转移过程中,左右脚的足底压力并不是对称的,如图5所示,因此,足底压力的不对称性在一定程度上反映了运动的不对称性,使理论计算数据与实际测量数据之间存在偏差,然而从实验结果来看,这种运动不对称性对于误差的影响并不大,在实际应用中,对于偏瘫和下肢功能障碍者,可能需要同时采集左右两侧的关节角度数据;另外,本研究力学模型的参数是根据受测者的体重和身高按照国家标准提供的回归方程求得,与实际人体的质量分布和体段参数存在较大差异,这也造成了误差。
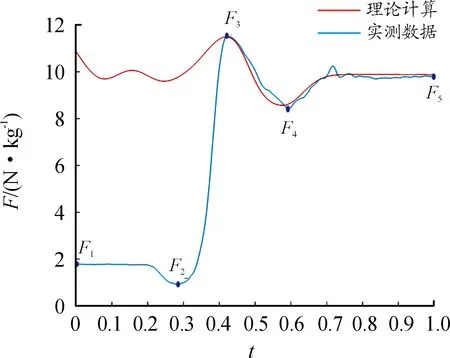
图4 1名受测者坐站转移的足底压力曲线
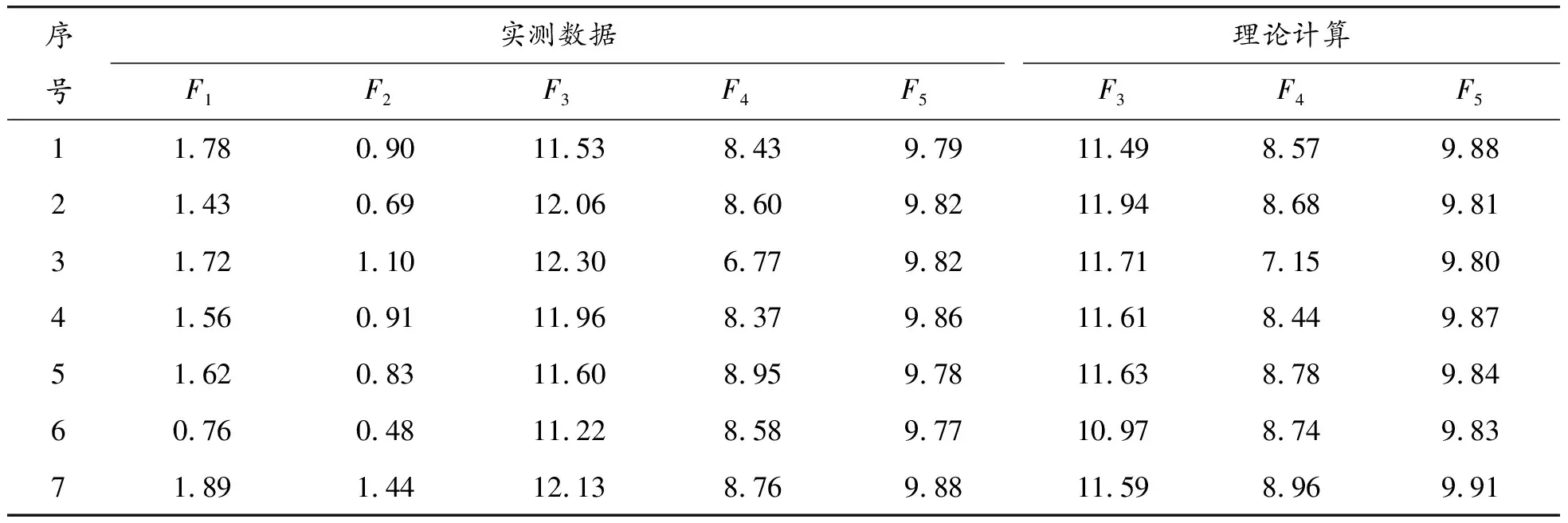
表4 7名受测者各时刻足底压力数据 N/kg

表5 7名受测者足底压力的理论计算与实测数据
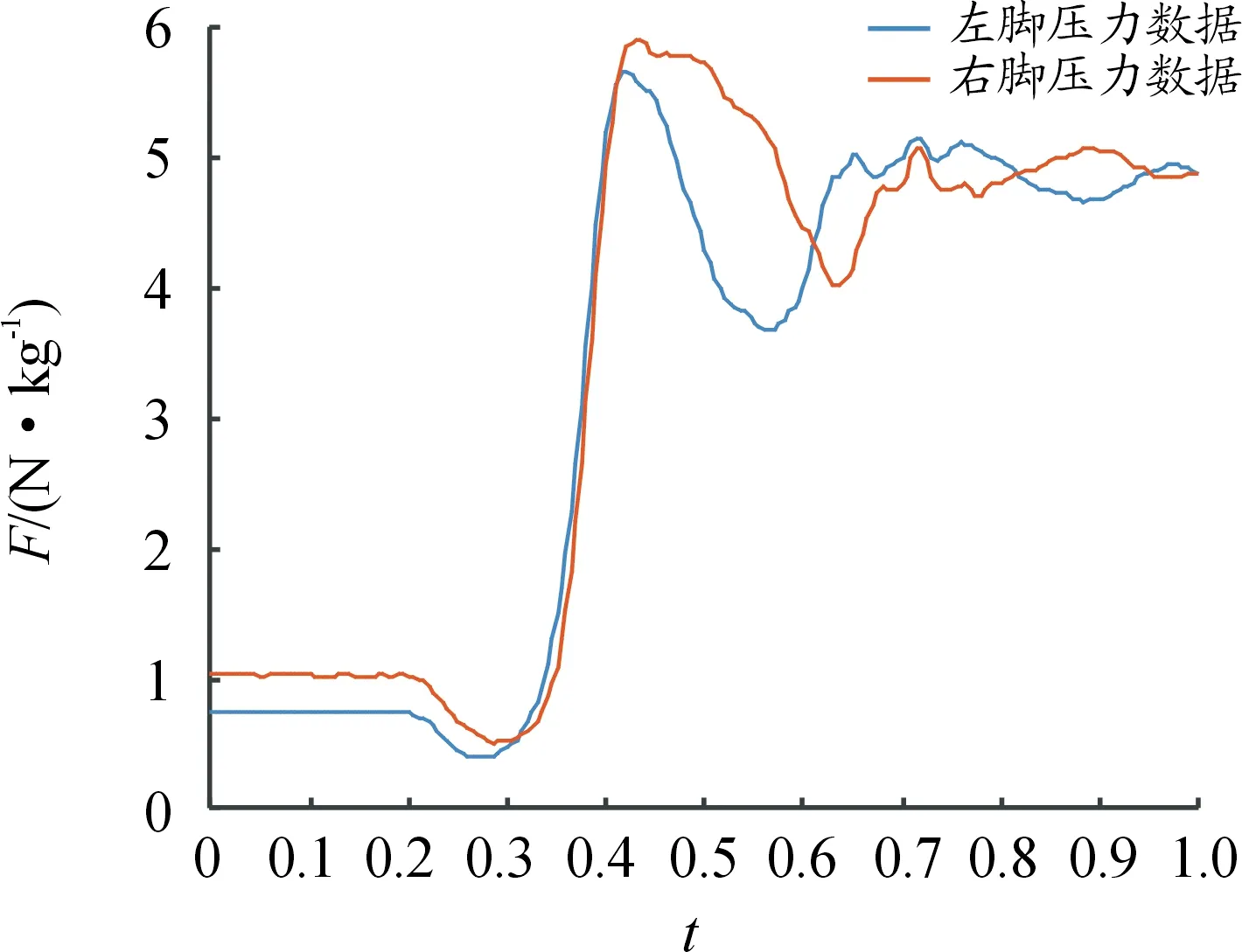
图5 1名受测者坐站转移的左、右脚足底压力曲线
在坐站转移运动中,关节峰值力矩是评估其下肢能力的重要指标[10],因此,将姿态传感器测得的关节角度数据代入式(20)~(22)中,根据表2中的人体各项体段参数,得到坐站转移过程中髋关节、膝关节和踝关节的力矩曲线,如图6所示。当人体离开座位前,由于没有考虑人体与座位之间的接触力,因此只绘出离开座位之后的膝关节和踝关节力矩曲线(逆时针方向为正),图中虚线表示离开座位的时刻;每个关节的力矩与身体质量乘以身高进行归一化,以便于不同体型受试者之间的比较。由图6可知,在坐站转移的开始阶段,髋关节力矩小于0.1 N·m/(kg·m),在躯干前倾阶段,髋关节力矩逐渐增大,在离开座位后很短一段时间内,髋关节力矩达到最大值,之后髋关节、膝关节和踝关节力矩逐渐减小,躯干、大腿和小腿逐渐伸直。7名受测者的关节最大峰值力矩见表5所列,在坐站转移实验中,7名受测者膝关节力矩峰值均大于1.0 N·m/(kg·m),其中有6名受测者的膝关节力矩峰值大于1.2 N·m/(kg·m),这是因为在坐站转移运动中,膝关节需要通过较大的角位移来使身体重心向上运动,这也意味着膝关节损伤患者在进行坐站转移运动时可能更容易跌倒。在7名受测者中,受测者1和受测者3的踝关节峰值力矩大于其髋关节峰值力矩,由表1可知,受测者1和受测者3的身高较其他受测者更高,这可能意味着更高的身高需要更大的踝关节力矩控制身体重心位于足底支撑面内。
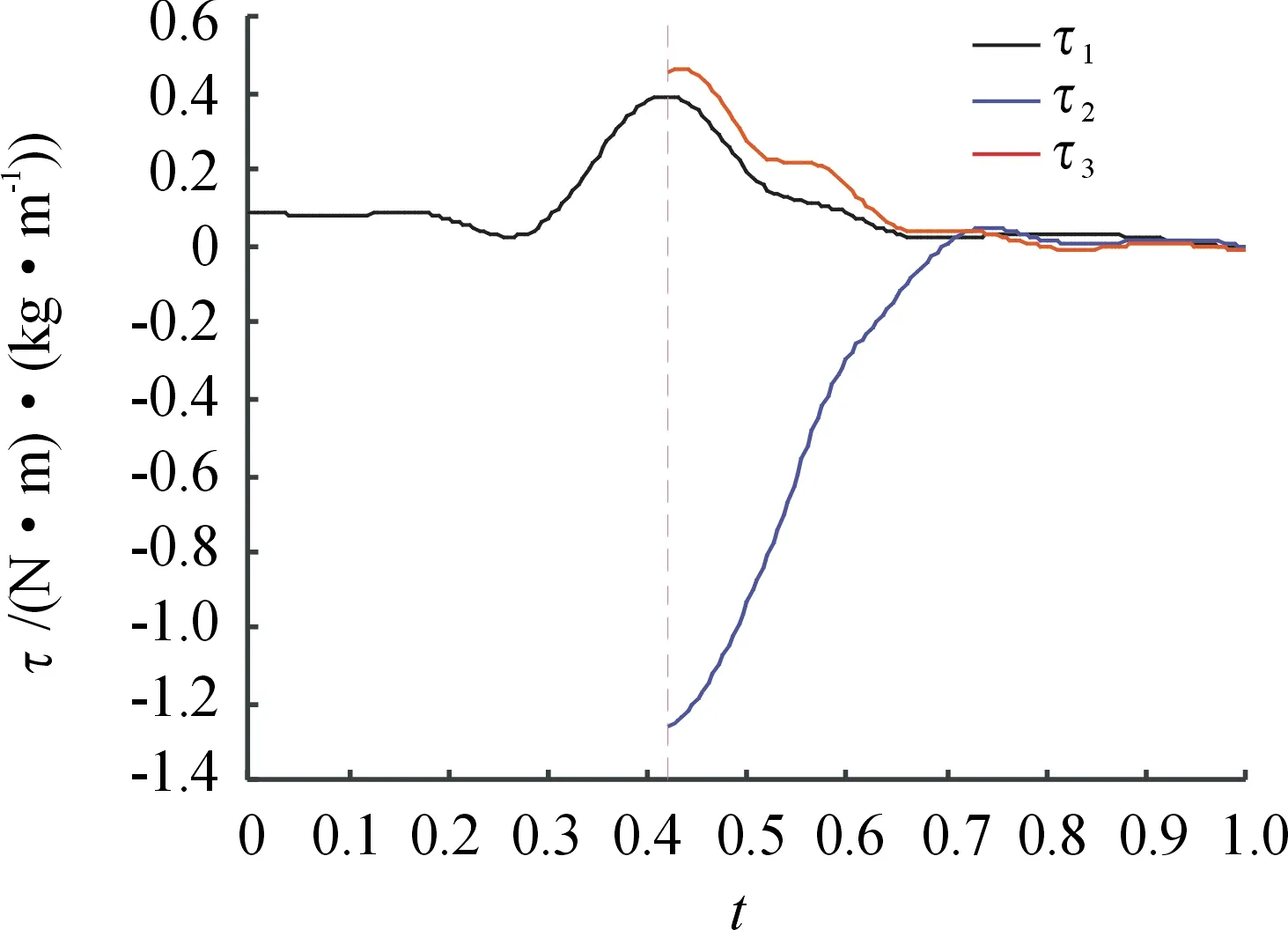
图6 1名受测者坐站转移的关节力矩曲线

表6 7名受测者的关节最大峰值力矩 N·m/(kg·m)
3 结论
搭建了一种基于姿态传感器的人体坐站转移运动测量系统,通过姿态传感器采集的姿态角解算人体坐站转移的下肢关节角度数据,利用足底测力踏板验证了基于姿态传感器的测量系统的可行性与有效性,实测地面反力数据与理论计算地面反力数据相关系数R≥0.91,均方根误差RMSE≤0.44,通过拉格朗日动力学方法计算了人体坐站转移过程中关节的最大峰值力矩,其中踝关节平均最大峰值力矩为(0.413±0.091)N·m/(kg·m),膝关节绝对平均最大峰值力矩为(1.241±0.076)N·m/(kg·m),髋关节最大峰值力矩为0.427±0.065 N·m/(kg·m)。
由于本研究的实验对象仅限于7名健康大学生,其运动学和动力学参数不足以涵盖所有人群,为了进一步提高基于姿态传感器的人体坐站转移测量系统的准确性,应对不同的群体开展更广泛的研究,以验证该系统的稳定性和可靠性。同时,应对坐站转移过程中下肢对称进一步研究,对于偏瘫及对于坐站转移障碍患者的平衡评估具有重要意义。
基于姿态传感器的人体坐站转移测量系统,相较于运动捕捉系统,更能满足临床的实际应用,为坐站转移康复评估提供了更加便利的方法,也可以为坐站康复训练器具的研发提供参考。
