注重数形结合创设灵动课堂
2021-09-13高国栋
摘 要:随着教育改革的稳健发展,如何创建灵动课堂,满足学生全面成长需求,成为教师需要思考与解决的育人难题之一.其中,数形结合作为经典数学思想及解题方法,在“以形助数”、“以数解形”基础上调用学生数学思维,解决具体问题,使学生推理能力、抽象思维能力、空间想象力、运算能力等核心素养随之增强,继而完成立德树人教改任务,数形结合教学实践价值可见一斑.本文通过探析初中数学教学中数形结合应用策略,以期创建灵动课堂,发展学生数学素养.
关键词:数形结合;初中数学;应用
中图分类号:G632 文献标识码:A 文章编号:1008-0333(2021)23-0014-02
收稿日期:2021-05-15
作者简介:高国栋(1985.9-),男,吉林省德惠人,本科,中学一级教师,从事中学数学教学研究.
数与形是数学研究两个基本对象,在一定条件下二者可自由转化,将数与形关联在一起,继而有效解决数学问题.华罗庚(著名数学家)曾说“数形结合百般好,隔裂分家万事休”.数与形在特定条件下是相互对应的关系,将抽象数量关系、数学语言与位置关系、直观几何图形联系到一起,在“以数解形”、“以形助数”基础上运用形象思维、抽象思维攻克解题难关,使抽象问题变得具体,复杂问题得以简化,有效优化解题途径.基于此,为提高初中数学教学质量,探析数形结合应用策略显得尤为重要.
一、初中数学课堂上数形结合应用必要性
1.降低学生数学知识学习及理解难度
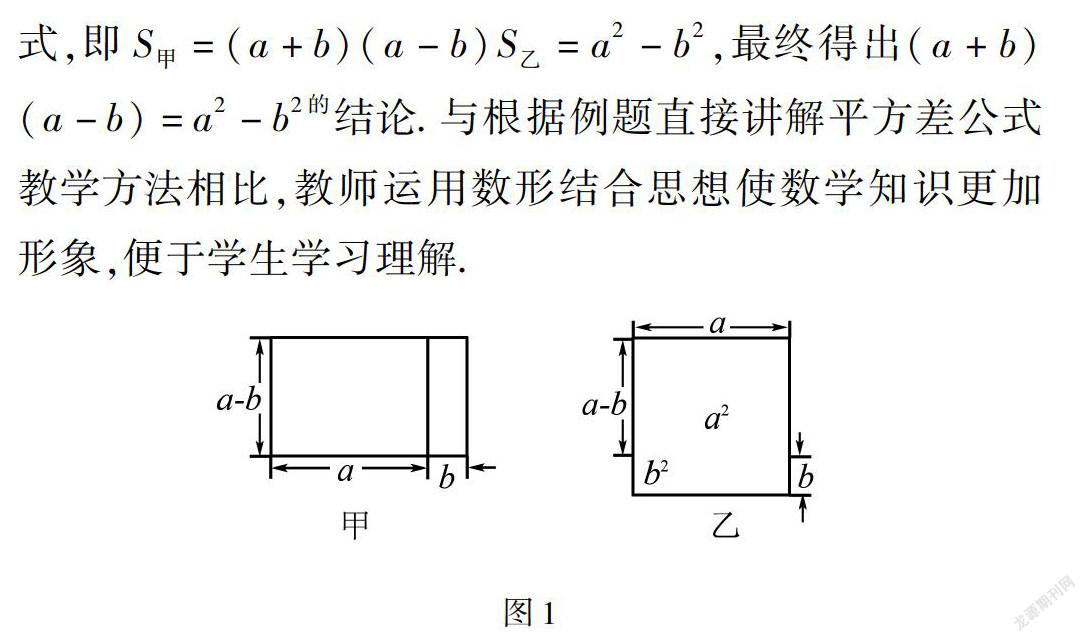
数学知识较为抽象,单纯通过文字很难理解其深意,加之学生数学学习基础不同,理解能力各异,徒增数学学习阻力.基于此,教师需在育人过程中应用数形结合理念,鼓励学生在理解抽象概念同时绘制直观几何图形,使数学知识更加通俗易懂,有效提高学生学习效率.例如,教师在讲解“平方差公式”时,若只要求学生硬性记忆公式将陷入灌输式教学误区,无法有效培养学生数学素养,为此教师可先引领学生“做一做”,将图1中甲图绿色长方形换到乙图上,根据两图面积关系直观说明平方差公式,即S甲=(a+b)(a-b)S乙=a2-b2,最终得出(a+b)(a-b)=a2-b2的结论.与根据例题直接讲解平方差公式教学方法相比,教师运用数形结合思想使数学知识更加形象,便于学生学习理解.
2.丰富初中数学教学模式
教学改革要求教师不断扩宽育人路径,根据教学实况有效创新育人方法,使知识传导效率得以提高,达到创建灵动课堂目的.例如,教师在进行“数据的收集与表示”教学时,可采用案例分析教学法,率先为学生讲述第28届悉尼奥运会上日本、美国、澳大利亚、俄罗斯、中国等国家金牌、银牌、铜牌数量,而后引领学生绘制统计表,在此基础上提出问题,即“如何直观体现各国金牌占比”,继而鼓励学生通过绘制扇形统计图、条形统计图體现数据统计分析结果,在此基础上树立数形结合意识,加上数据收集与表示训练,提升学生数据分析能力、创新实践等能力,通过应用数形结合教学方法落实育人目标.
二、初中数学课堂上数形结合应用的关键
1.以人为本,及时启发
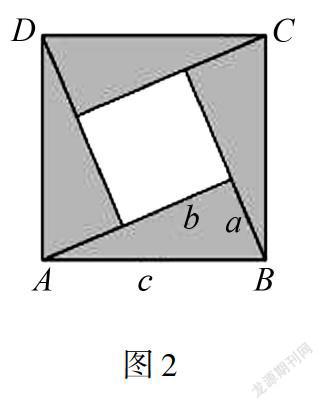
为保障学生能树立数形结合意识,教师需开发学生思维灵活性、开阔性,让学生能积极参与数学教学活动,用抽象思维及形象思维解决数学问题.基于此,教师需发挥引导、启发、鼓励作用,助力学生图2攻克数学学习难关,使学生有信心、有能力应用数形结合方法.例如,教师在进行“勾股定理”教学时,可创建师生互动自由探知教学环境,让学生剪出4个全等直角三角形并拼成图2所示形状,启发学生利用面积证明勾股定理.S正方形=c2,也可用2ab+(a+b)2表示,则c2=2ab+(a-b)2,最终得出c2=a2+b2结论.在学生完成证明任务后教师还可鼓励学生多角度解决证明问题,助力学生灵活运用数形结合方法,提升个人数学素养.
2.立足教材,突出能力
为保障数形结合的应用与初中数学教学目标一致,教师需加大教材研读力度,找准数形结合育人立足点,做好教学规划,有目的、有计划的应用数形结合.旨在构建灵动课堂,渗透立德树人理念,在激活学生抽象思维、形象思维前提下,培养学生数学核心素养,如运算能力、直观想象、数据分析等.
三、初中数学课堂上数形结合应用策略
1.在教学导入环节应用数形结合理念
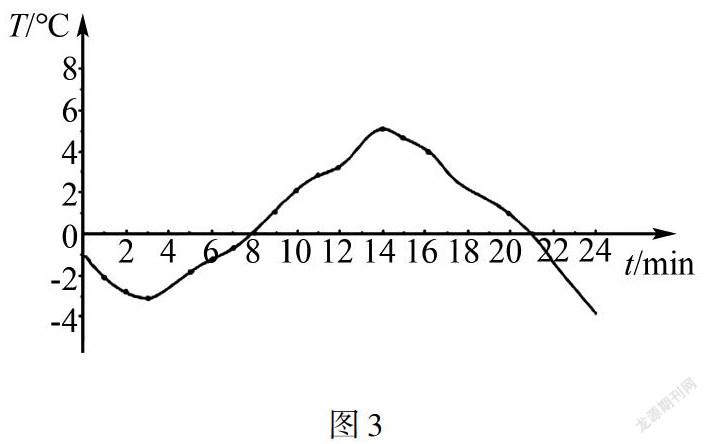
良好的教学导入可起到事半功倍育人效果,为学生进入数学知识的世界搭建桥梁.与抽象数学概念相比,图形更加直观且具有感染力,能帮助学生降低数学知识的理解难度,为此教师可在教学导入环节应用数形结合.例如,教师在进行“函数及其图像”教学时,可率先研读教材明确教学重难点,即掌握函数图像画法,能在观察图像中获取信息,而后通过问题导入教学内容,引领学生观察图3并提出问题,即“从图中怎样获悉不同时间气温信息”.图3为直角坐标系,横轴为t,纵轴为T,该图实则给出二者函数关系,如10点温度为2℃,对应点的坐标为(10,2),说明在t为10时,函数对应值T为2,继而简化数学知识,使学生对函数及其图像知识有所了解,为学生深入学习奠定基础.
2.在讲解数学知识环节应用数形结合理念
数形结合具有灵动性、启发性、渗透性等特点,可在数形互换过程中发挥育人作用,这就需要教师根据育人需求,挖掘数形结合理念的教学实践潜力,旨在构建灵动课堂,助推学生全面成长.例如,教师在进行“平行四边形的认识” “矩形”教学时,为使学生能牢记平行四边形特征并了解其与矩形的关系,可制作教具,用图钉将四根长方形硬纸板固定住,得到平行四边形,而后引领学生观察思考在任意一点施加力图形会发生怎样的变化,通过探讨及实际操作学生会发现角的大小发生改变,同时对边仍然平行,平行四边形性质并未改变.在此前提下,教师追问若改变图形内角,使之成为直角,会得当什么样的平行四边形,继而为学生探索矩形铺平道路,通过与平行四边形特征进行对比牢记基础知识.
3.在课后复习过程中应用数形结合理念
课后复习是学生牢记数学知识,通过反复练习强化数学素养的重要渠道,为此,教师需在学生树立数形结合意识前提下,鼓励学生运用该方法进行课后练习,使学生能将数形结合视为解决数学问题的工具,灵活运用数学思维攻克学习难关.
综上所述,在初中数学教学中注重数形结合具有降低学生数学知识学习及理解难度,丰富初中数学教学模式积极意义.这就需要教师紧抓以人为本、突出能力教学,在教学导入、知识讲解、课后练习过程中灵活运用数形结合理念,引领学生树立数形结合意识,将其视为解题工具,在完成教学任务基础上培养学生数学思维能力、直观想象、运算、逻辑推理等核心素养,达到提高初中数学新时代教育改革的目的.
参考文献:
[1]陈玲玲.巧用数形结合思想提升学生说理能力[J].考试周刊,2020(52):51-52.
[2]蔡晓琼.让数形结合思想渗透初中数学课堂[J].数学大世界(下旬版),2019(10):78.
[责任编辑:李 璟]
