波形钢腹板钢−混凝土简支组合箱梁抗弯承载力分析

周旺保，许添鑫，谭志化，钟天璇，刘韶辉，蒋丽忠

(1. 中南大学 土木工程学院，湖南 长沙410075；2. 高速铁路建造技术国家工程实验室，湖南 长沙410075；3. 深圳地铁建设集团有限公司，广东 深圳518000)

波形钢腹板钢−混凝土简支组合箱梁(以下简称波形钢腹板组合箱梁)的腹板较薄，抗扭刚度、延性等力学性能较高。与平腹板相比，其所需腹板加劲肋大大减少，有着更轻的自重和更优的经济效益，在桥梁和建筑结构中应用广泛[1−3]。波形钢腹板组合箱梁的抗弯承载力是结构设计分析中的关键力学性能指标之一，因此对波形钢腹板组合箱梁的抗弯承载力进行试验研究，并在此基础上进一步开展有限元建模及理论分析十分重要。自20 世纪80 年代以来，波形钢腹板在土建行业，尤其是桥梁和建筑的应用与研究开始快速发展，目前关于波形钢腹板组合箱梁受力性能的研究已取得了一些成果。JOHNSON 等[4]建立了波形钢腹板梁的有限元模型，提出了计算波形钢腹板有效剪切模量的方法，在参数分析的基础上得出波形钢腹板的剪切模量约为平钢腹板剪切模量的0.9 倍的结论。吴文清等[5]在试验研究的基础上，总结了波形钢腹板组合梁截面的正应变分布规律，并提出弹性阶段波形钢腹板组合梁截面的正应变符合“拟平截面假定”的结论。KIM 等[6]以腹板波形为主要参数，进行了波形钢腹板预应力组合梁的抗弯试验，由结果分析发现波形钢腹板的“手风琴效应”能增强结构抵抗局部和平面外屈曲的能力，且波形钢腹板的倾斜板会产生轴向应力，从而提高钢梁与混凝土板之间共同工作的能力。林梦凯等[7]通过室内模型静载试验与有限元建模，对波形钢腹板的手风琴效应进行了深入的分析，并得出适度调整波形钢腹板的尺寸可以使手风琴效应更加明显的结论。聂鑫等[8]提出将受拉的混凝土底板替换成钢板的新型构造形式，并进行了抗弯承载力试验研究，结果表明，这种新型结构在承载能力、抗裂性能、经济效益等方面均优于传统的波形钢腹板箱梁。OLIVEIRA 等[9]建立了波纹正弦腹板钢−混凝土连续组合梁的有限元模型，计算了弹性临界弯矩并与已有文献中的数据进行了对比验证。王鹏[10]在试验研究的基础上进行了有限元建模分析，发现波形钢腹板组合箱梁的剪力滞效应受到跨高比的显著影响。刘保东等[11]对弯剪组合作用下的波形钢腹板连续组合箱梁进行了试验研究。由试验现象可知，组合箱梁截面剪力发生了重分布，波形钢腹板将承受混凝土区域的部分剪力。目前关于波形钢腹板组合箱梁抗弯承载力的试验研究及理论研究较少。本文在波形钢腹板组合箱梁的竖向加载试验基础上，建立合理的有限元模型，并进一步在试验研究、仿真分析及理论分析的基础上，提出了波形钢腹板组合箱梁抗弯承载力的简化公式。

1 试验及有限元模型

1.1 试验概况

为研究波形钢腹板组合箱梁的抗弯性能，以剪力连接度为主要考察参数对3榀波形钢腹板组合箱梁试件进行了竖向加载试验，试件的详细参数如表1，其中l为试件的计算跨度，bc为混凝土板宽度，hc为混凝土板高度，btf为钢梁的上翼缘宽度，ttf为钢梁的上翼缘厚度，bbf为钢梁的下底板宽度，tbf为钢梁的下底板厚度，hw为腹板高度，tw为腹板厚度，d为栓钉直径，ρz为混凝土板纵向配筋率，ρh为混凝土板横向配筋率，剪力连接度r=nr/nf，nf为构件完全连接时所需的栓钉的个数，nr为构件内实配栓钉的个数，试件的横截面参数见图1，波形钢腹板尺寸见图2。

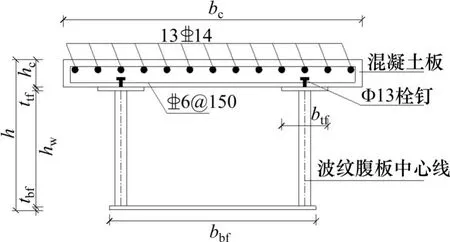
图1 试件横截面Fig.1 Cross-section of specimens

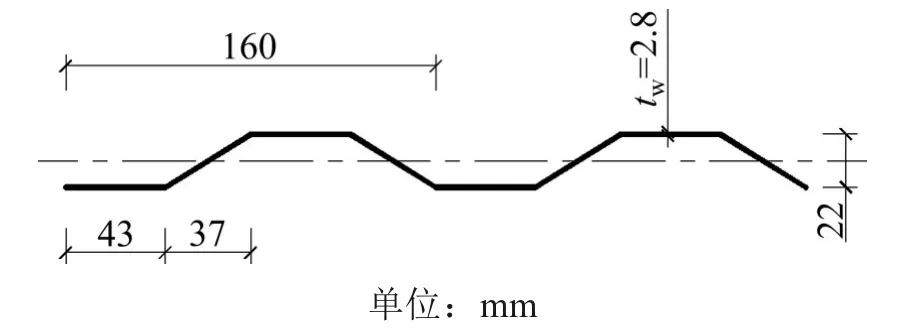
图2 波形钢腹板尺寸Fig.2 Dimensions of corrugated steel web

表1 试件参数Table 1 Parameters of specimens

试验采用C30级商品混凝土，浇筑试件构件的同时分别制作3组标准立方体抗压试块和棱柱体试块，与试件在同等条件下养护，由材料试验实测得混凝土弹性模量Ec= 3.06 × 104MPa,立方体抗压强度fcu= 30.6 MPa，轴心抗压强度fc=20.1 MPa，轴心抗拉强度ft= 2.01MPa。钢材的材料特性由标准拉伸试验测得，制备3组标准试件，每组各3个。钢材材性试验的结果如表2所示。

表2 钢材材性试验结果Table 2 Steel material properties test results

本试验使用力−位移混合控制加载方法对构件进行三分点竖向加载，在试件没有屈服前使用荷载控制，荷载循环1次；在试件屈服后采用位移控制，前3 级循环3 次，之后循环2 次，直至荷载下降至极限荷载的85%左右或试件破坏时，结束试验，加载制度如图3所示。主要测试内容为混凝土和钢梁在支座处、1/3位置处和1/2位置处的竖向位移，通过布置激光位移计测定位移，布置见图4，荷载数据为MTS读数。试验现场装置图见图5。

图3 试验加载制度Fig.3 Test loading system

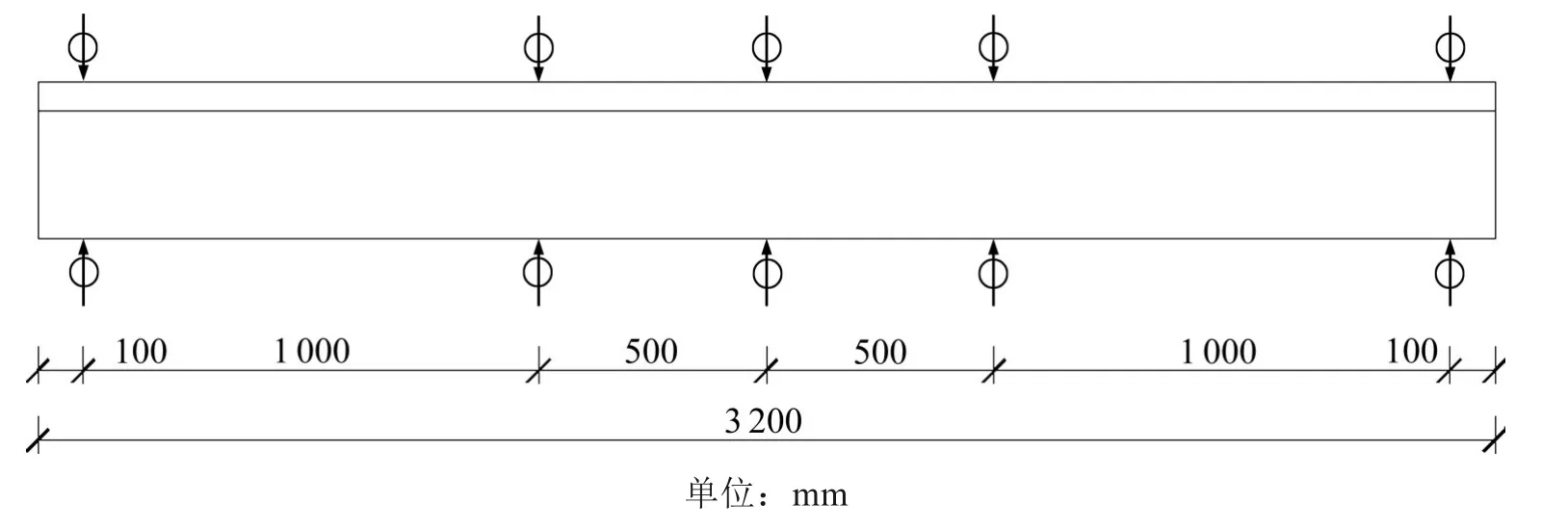
图4 竖向位移测点布置图Fig.4 Arrangement of vertical displacement points

图5 试验现场装置Fig.5 Test site device

1.2 有限元模型

限于试验数据与参数较少，本文采用ANSYS对CSWCB 的抗弯承载力进行有限元扩展参数分析，试件整体有限元模型如图6所示。混凝土板采用3D 加筋混凝土实体单元SOLID65 模拟，混凝土的本构关系模型采用多线性等向强化模型(MISO)，其应力−应变关系采用E.Hognestad模型[12]：

图6 整体有限元模型Fig.6 Global finite element model

式中：ε0为峰值应力时对应的应变，取ε0= 0.002；εcu为极限压应变，取εcu= 0.0033。

钢梁的上翼缘、下底板和波形钢腹板采用4节点有限应变壳单元SHELL181进行模拟，钢筋采用3D 杆单元LINK8 模拟。钢梁和钢筋的本构关系模型采用理想弹塑性模型，应力−应变关系如图7 所示，图中：σy为屈服应力，εy为屈服应变。

图7 钢梁和钢筋的本构曲线Fig.7 Constitutive curve of steel beams and steel reinforcement

混凝土板与钢梁之间的剪力连接件采用非线性弹簧单元COMBIN39 模拟，通过定义单元实常数来模拟栓钉的剪切变形，栓钉的剪力—滑移曲线表达式为[13]：

式中：Ve为弹簧单元的剪力；nc为弹簧单元个数；Vu为单个栓钉受剪承载力；τ为弹簧单元的相对滑移量；Ast为栓钉截面面积；fs为栓钉抗拉强度设计值；κ为强屈比，可取κ=fsy/fsu；fsy为栓钉屈服强度；fsu为栓钉抗拉强度。栓钉的剪力−滑移曲线如图8所示。

图8 栓钉剪力−滑移曲线Fig.8 Stud shear force-slip curve

利用有限元模型对波形钢腹板组合箱梁的跨中截面荷载−位移曲线进行了计算，并将计算结果与试验实测值进行了比对，结果如图9 和表3 所示。表中：Pu为抗弯承载力的试验值，Pe,u为抗弯承载力的数值结果；ζp=(Pu−Pe,u)/Pu为抗弯承载力试验值与数值结果的误差，δ为抗弯承载力的试验值所对应的位移；δe为抗弯承载力数值结果所对应的位移。由图9 和表3 可知，有限元模型计算结果曲线与试验结果吻合良好，论证了有限元计算模型的有效性。

图9 试验值与有限元数值结果的荷载−位移曲线对比Fig.9 Load-displacement curves comparison between test results and finite element results

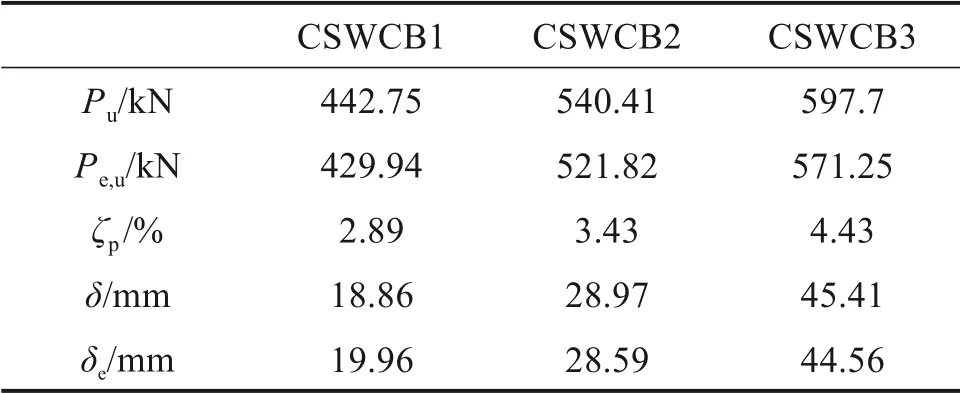
表3 抗弯承载力、极限位移的有限元与试验结果对比Table 3 Comparison of finite element model and test results of flexural bearing capacity and ultimate displacement

2 极限承载力计算公式

基本假定：1) 混凝土板和钢梁符合“拟平截面假定”[5]；2)混凝土板受拉区不参与受力；3)考虑手风琴效应，忽略波形钢腹板的轴向抗弯刚度[14]。

2.1 完全剪力连接情况下抗弯承载力计算公式

完全剪力连接情况下波形钢腹板组合箱梁截面塑性中和轴有2种分布情况：位于混凝土板内和位于钢梁内，对应的抗弯承载力计算方法分别如下：

1)截面塑性中和轴位于混凝土板内，即Asff≤bchcfc时，计算简图如图10所示。

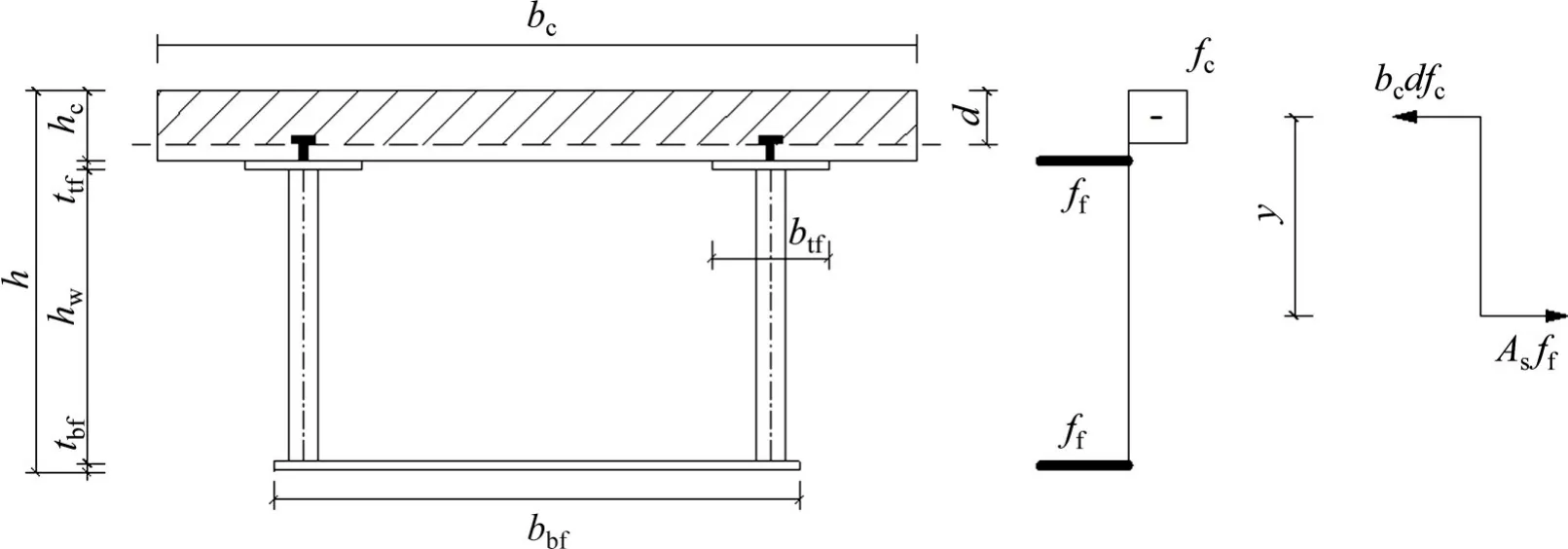
图10 塑性中和轴位于混凝土板内的计算简图Fig.10 Calculation diagram of the plastic neutral axis located in the concrete slab

根据轴力平衡得：

截面抗弯承载力可表示为：

式中：h为波形钢腹板组合箱梁整体高度；hs为钢梁高度；d为混凝土板顶到波形钢腹板组合箱梁截面塑性中和轴的距离；y为混凝土受压区的截面应力合力到钢梁截面应力合力的距离；As为钢梁截面面积；ff为钢材屈服强度。

2) 截面塑性中和轴位于钢梁内，即Asff>bchcfc时，计算简图如图11所示。

图11 塑性中和轴位于钢梁内的计算简图Fig.11 Calculation diagram of the plastic neutral axis located in steel beam

根据轴力平衡得

①当(As-A′s)ff

②当(As-A′s)ff>bchcfc+A′sff时，有：

联立式(7)，(8)或(9)可得截面抗弯承载力为：

式中：A′s为钢梁受压区面积；z1为钢梁受拉区应力合力至混凝土板截面应力合力的距离；z2为钢梁受拉区截面应力合力至钢梁受压区截面应力合力的距离；f1为钢梁受拉区截面应力；f2为钢梁受压区截面应力。

利用本文提出的计算方法对多个具有不同腹板高厚比的波形钢腹板组合箱梁试件进行了计算，并将其计算结果与有限元计算结果进行了比较，如表4 所示。表中MFE为波形钢腹板组合箱梁抗弯承载力的有限元计算结果，M为本文解析方法计算结果，ξt= 100(MFE-M)/MFE。由表4 可知，解析方法计算结果与有限元数值结果吻合良好，验证了本文解析计算方法的有效性。

表4 不同腹板高度下理论公式与有限元结果对比Table 4 Comparison of the oretical and finite element results under different corrugated web heights

2.2 部分剪力连接情况下抗弯承载力计算公式

为考虑剪力连接度对波形钢腹板组合箱梁截面抗弯承载力的影响，利用剪力连接度的幂函数对完全剪力连接情况下波形钢腹板组合箱梁截面抗弯承载力计算公式进行内插修正[15]，修正后部分剪力连接度情况下的波形钢腹板组合箱梁截面抗弯承载力可表示为：

式中：Mfu为完全剪力连接时波形钢腹板组合箱梁的塑性极限弯矩；Msu为钢梁的塑性极限弯矩，nf=V/Nv，V为混凝土板与钢梁间的纵向剪力；参照《钢–混凝土组合结构设计规程》(DL/T 5085—1999)进行计算，α取值如下[16]：

式中：fcu为混凝土立方体抗压强度。

将部分剪力连接下波形钢腹板组合箱梁抗弯承载力的解析方法计算结果与试验结果进行比对，比较结果如表5 所示。表中ξt= 100(Mu-Mu.t)/Mu，Mu.t为理论公式计算结果，实际剪力连接度大于1时按r= 1计算。由表5可知，解析方法计算结果与试验结果吻合良好，论证了解析方法的有效性。

表5 部分剪力连接下波形钢腹板组合箱梁抗弯承载力Table 5 Positive flexural bearing capacity of composite box girders with corrugated steel webs with partial shear connection

3 结论

1) 分别建立了完全剪力连接和部分剪力连接情况下波形钢腹板组合箱梁截面抗弯承载力计算公式，并与试验值和有限元数值结果进行了比较，论证了计算公式的有效性，同时，公式形式简单，便于手算，可为波形钢腹板组合箱梁截面的工程设计提供参考。

2) 利用剪力连接度幂函数内插修正方法，可有效考虑剪力连接度对波形钢腹板组合箱梁抗弯承载力的折减效应。

3) 剪力连接度对波形钢腹板组合箱梁的截面抗弯承载力有显著影响，随着剪力连接度的增大，波形钢腹板组合箱梁截面的极限承载能力显著提高。