斜腹板箱形梁桥腹板剪力分布的空间三维有限元分析

李政伟， 王海君， 张 海

(1. 暨南大学 力学与建筑工程学院， 广州 510632； 2. 广州交通投资集团有限公司， 广州 510288)

混凝土箱形截面具有良好的抗弯和抗扭特性，已成为大中跨径混凝土桥梁设计的首选桥梁结构形式，众多学者对混凝土箱形梁桥开展了多方面研究[1-6].一个单箱多室的箱形截面由多个腹板和多个箱室组成，其空间力学性能复杂.研究剪力在箱室内各个腹板间的分布，对确保单箱多室箱形截面各个腹板能有效、协同工作有着重要意义.对于箱形梁桥，许多学者对箱形截面的剪切滞、有效宽度[7-10]和活荷载剪力分配方面进行了研究[11-13].

一般情况下，认为自重及二期恒载在箱梁各个部分的剪力分布是均匀的，也就是箱梁各个腹板平均承担整个截面所受的剪力.但这种传统观点在研究中经过证明是不恰当的，Xue等[14-15]通过三维有限元数值分析得出，剪力在各个腹板间承担的剪力大小是不一样的，甚至差别很大，这就导致多承担剪力的腹板可能在设计上偏于不安全.

斜腹板混凝土箱形梁桥在城市中大量应用，斜腹板箱形截面一方面增大了结构的挑臂，另一方面也比较美观.本文采用三维有限元分析手段，对不同条件下多个单箱多室箱梁进行计算分析，在得到的各道腹板实际分担剪力分析和总结的基础上，得到单箱多室箱梁的腹板剪力分配规律，并给出相关的设计建议.

1 研究方法与模型建立

箱梁受力相对复杂，采用常规箱梁设计理论，仅能得到典型断面特定条件下的分析结果，无法得到全桥截面的内力变化，不能体现支承条件等因素的影响，因此采用空间有限元方法对剪力的实际分布进行研究.图1为局部内力总和结果.一般三维有限元实体单元分析结果只能输出应力，不能输出内力，研究腹板剪力分配规律需要提取各道腹板的剪力，本文采用Midas程序自带的“局部方向内力总和”功能来实现，“局部方向内力总和”可以直接输出所剖截面内力总和，提取得到所需要的剪力值，其步骤为：

图1 局部内力总和结果Fig.1 Results for sum of local internal forces

1) 在模型分析完成的后处理中，选择“后处理”的“局部方向内力总和”；

2) 通过创建由三点构成的面，该面与箱梁相交，即完成在箱梁中截取截面；

3) 在“局部方向内力总和”功能菜单中选择截取得到的截面，点击“文本”，即输出所剖截面内力总和，程序即可输出激活单元的、待提取剪力腹板的内力总和.

通过三维有限元数值分析，对不同腹板厚度、不同箱室数量、不同边界条件及不同横梁刚度进行分析可得：边腹板承担的剪力比平均剪力(总剪力/腹板道数)要大，甚至大得多；边界条件和箱室数量显著影响着腹板剪力的分布.

因此，结合上述研究结论及本文研究对象斜腹板箱形截面，本文开展了边界条件、箱室数量、边腹板斜度等条件下单箱多室箱梁各道腹板分担的剪力值大小进行提取，并总结得到腹板剪力的分配规律.

基本简支箱梁参数为：跨径30 m，梁高1.8 m，顶板、底板厚25 cm.跨中标准段长13.6 m，腹板变宽段长4.0 m，腹板加宽段长3.0 m，端横梁长1.2 m.边界条件、箱室数量下对应的不同边腹板斜度为研究变化参数.各个条件下的分析模型如下：

1) 分别采用两组对比模型，分析在边腹板倾斜角度为0°、10°、15°、20°、25°等情况下，支承条件对腹板剪力分配影响：①单箱四室三支座模型与单箱四室双支座模型，即B4S2组模型与B4S3组模型进行对比分析；②单箱三室三支座模型与单箱三室双支座模型，即B3S2组模型与B3S3组模型进行对比分析.

2) 分别采用两组对比模型，分析在边腹板倾斜角度为0°、10°、15°、20°、25°等情况下，箱室数量对腹板剪力分配影响：①单箱四室三支座模型与单箱三室三支座模型，即B4S3组模型与B3S3组模型进行对比分析；②单箱四室双支座模型与单箱三室双支座模型，即B4S2组模型与B3S2组模型进行对比分析.

上述计算模型的断面图如图2所示(单位：cm).表1为剪力分布计算的20个模型的主要参数.本文研究恒载下箱梁结构腹板的剪力分布情况，因此，施加的荷载为主梁自重及二期恒载.二期恒载包含桥面调平层及现浇沥青层，按3.5 kN/m2计.结构计算模型图如图3a所示.提取腹板剪力的主梁截面，根据《公路桥规》斜截面计算复核截面的要求，选取最为典型的距离支座2h/3处的截面，h为梁高，如图3b所示.

图3 腹板剪力分布有限元分析计算模型Fig.3 Finite element analysis and calculation model for web shear force distribution

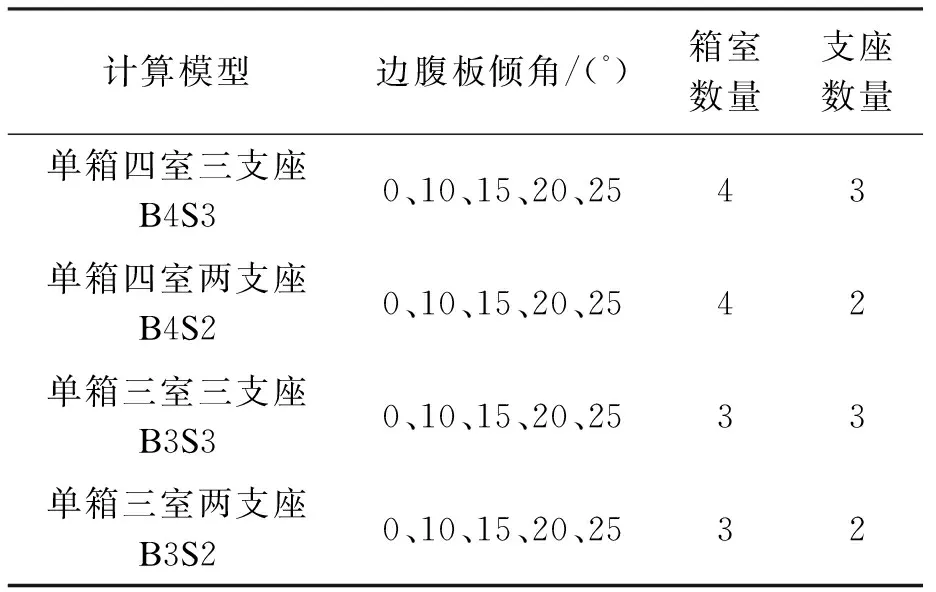
表1 计算模型参数Tab.1 Calculation model parameters

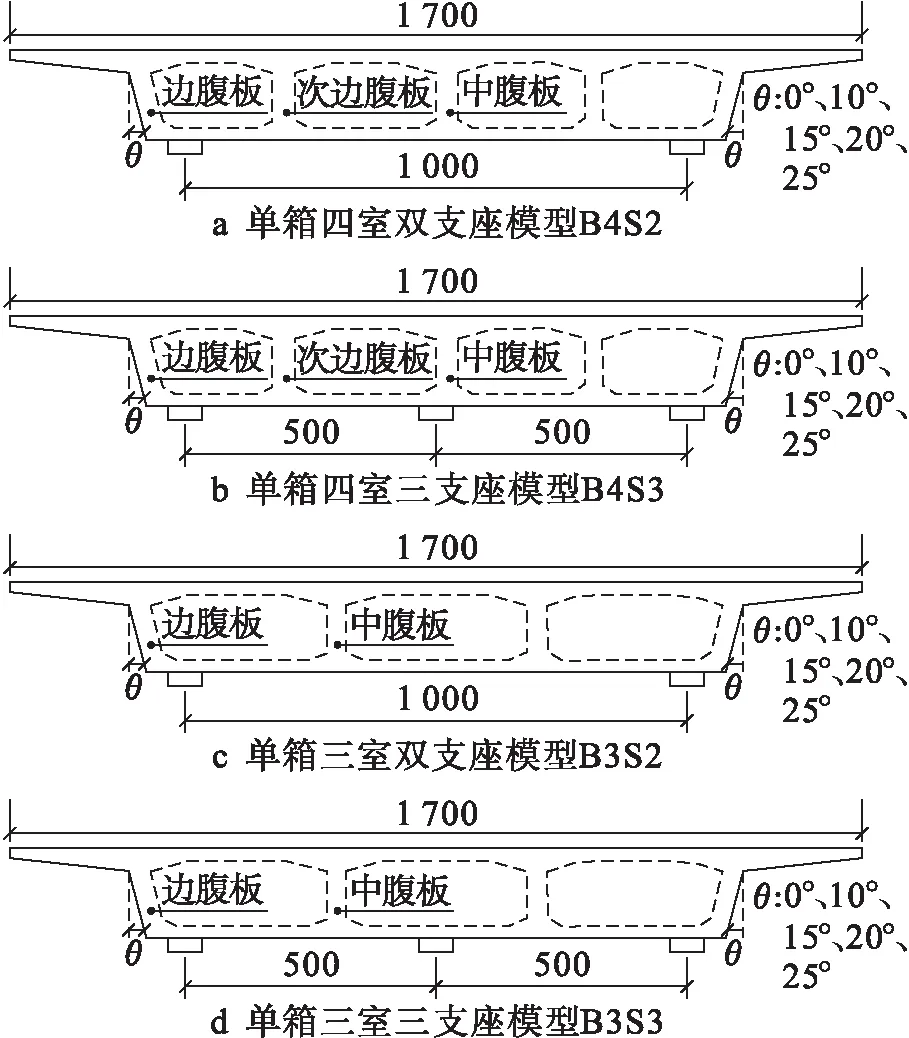
图2 腹板剪力分布分析模型Fig.2 Analysis model of web shear distribution

2 斜腹板箱梁剪力分配规律

Xue等[14-15]将单道腹板平均分担的剪力定义为

Va=Vt/Nf

(1)

式中：Va为每道腹板平均分配的理论剪力值；Vt为全截面剪力值；Nf为箱梁腹板的道数.同时定义了腹板剪力增大系数η为

η=Vi/Va

(2)

式中，Vi为单道腹板的剪力值.

表2～5分别列举了B4S3、B4S2、B3S3、B3S2系列腹板剪力分布计算模型的计算结果.将表格内容进行分析总结，并将必要的数据整理成图，可得如下结论：

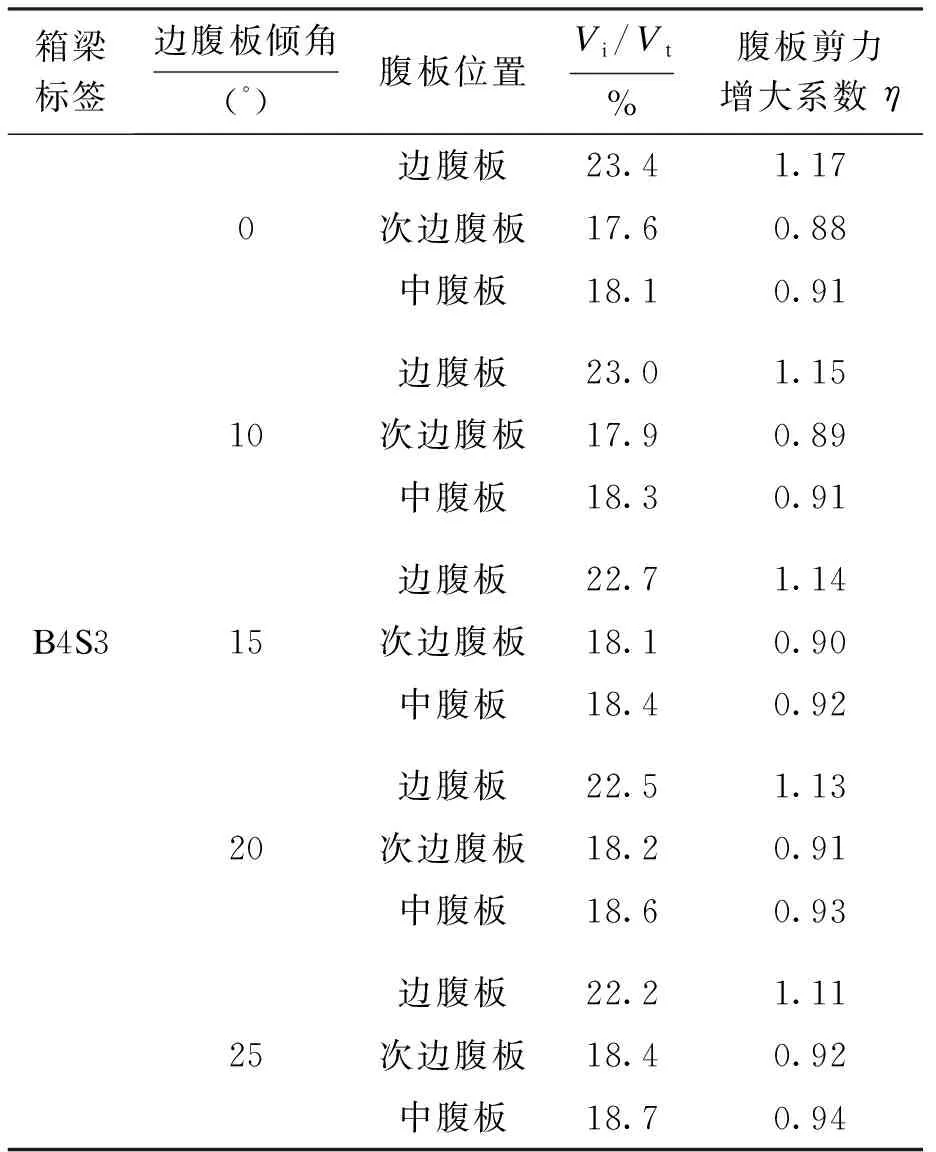
表2 B4S3模型腹板剪力分布计算结果Tab.2 Calculation results of web shear force distribution for B4S3 model

1) 边腹板剪力增大系数η均大于1，也就是说边腹板承担着较平均剪力大的剪力值，在设计中偏于不安全.由表3可知，在单箱四室双支座模型中，腹板剪力增大系数η甚至达1.31.因此在设计中，腹板剪力分配不均的问题应该引起足够重视.

表3 B4S2模型腹板剪力分布计算结果Tab.3 Calculation results of web shear force distribution for B4S2 model

2) 边腹板斜率对剪力增大系数η的影响.图4为单箱四室三支座模型(B4S3)的边腹板、次边腹板及中腹板的剪力增大系数η与边腹板斜率的关系.

由图4的趋势线可见，随着斜腹板斜率的增大，边腹板承担的剪力减小，次边腹板与中腹板承担的剪力增大.随着边腹板斜率增大，剪力增大系数η变化值很小，如B4S3-0°与B4S3-25°边腹板剪力增大系数η由1.17变为1.11，相差仅为5.13%.其他剪力分布分析模型系列也呈现相似规律，边腹板斜率对剪力增大系数η的影响不大.

图4 B4S3模型腹板剪力增大系数Fig.4 Shear force increase coefficient of web in B4S3 model

表4 B3S3模型腹板剪力分布计算结果Tab.4 Calculation results of web shear force distribution for B3S3 model

3) 边界对边腹板剪力增大系数η的影响.图5为两种箱室分别在三支座和双支座情况下边腹板剪力增大系数η的对比图.随着支座数量的增多，使得梁端支座反力在腹板中的分布更为均匀，因而多支座可有效降低边腹板承担剪力的比例，对设计更为有力.在单箱四室和单箱三室两种情况下，三支座的边腹板斜率对剪力增大系数η分别比两支座的降低9.6%～10.7%和6.4%～7.2%.

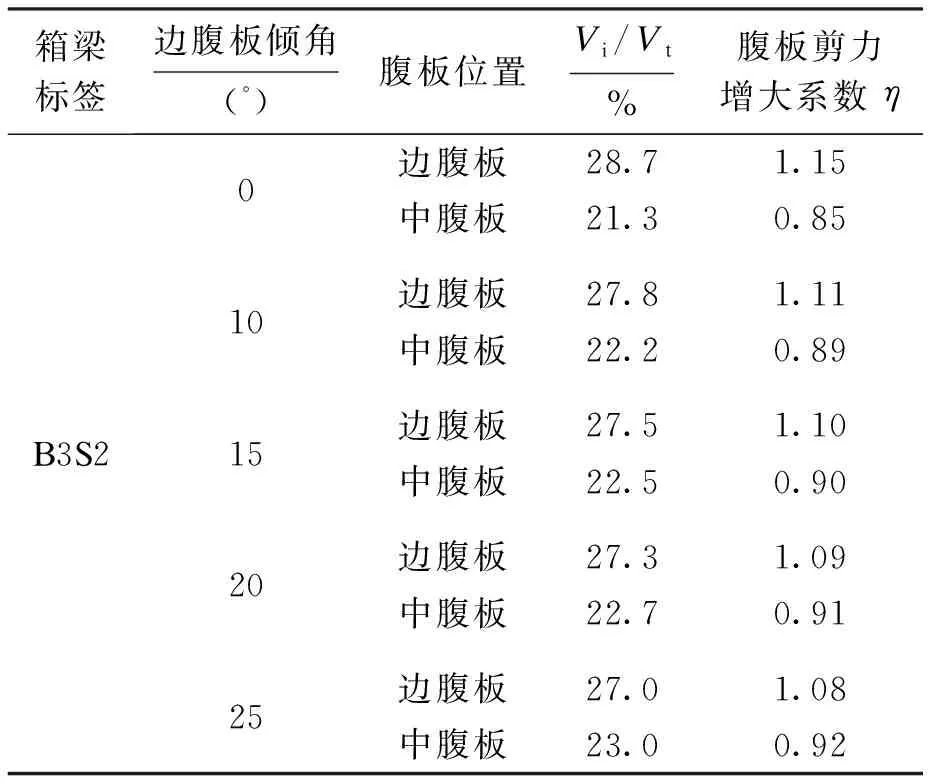
表5 B3S2模型腹板剪力分布计算结果Tab.5 Calculation results of web shear force distribution for B3S2 model

图5 边腹板剪力分布对比(边界的影响)Fig.5 Comparison of shear distribution of side webs (effect of boundary)

4) 箱室数量对边腹板剪力增大系数η的影响.图6为一定支座条件下分别在四箱和三箱情况下边腹板剪力增大系数η的对比图.由图6可知，箱室数量也是影响边腹板剪力增大系数η的重要影响因素.箱室变为三箱后，边腹板的承载桥面的宽度与中间腹板(次边腹板和中腹板)之比更为接近，因而对边腹板剪力增大系数η的影响也变得较小，剪力分布趋于均匀分布.在两支座和三支座两种情况下，单箱三室的边腹板斜率对剪力增大系数η分别比单箱四室的降低12.2%～13.4%和8.5%～10.4%.

图6 边腹板剪力分布对比(箱室数量的影响)Fig.6 Comparison of shear distribution of side webs (effect of chamber number)

3 结 论

为了探究不同边腹板斜度、边界条件、箱室数量对斜腹板箱梁腹板剪力的影响规律，在三维有限元分析模型中，采用“局部内力总和”的办法提取各个腹板剪力，得到如下结论：

1) 利用腹板剪力增大系数η表达单个腹板承担剪力的大小，概念清晰，利于把握.用于腹板设计、衡量腹板抗剪安全有着基本的概念作用.

2) 边腹板剪力增大系数η一般均大于1，抗剪设计中偏不安全.抗剪为脆性或准脆性破坏，因此，抗剪设计中应充分考虑边腹板剪力增大系数大于平均剪力的问题.

3) 边界条件、箱室数量对腹板剪力增大系数η有较大影响，箱梁截面方案优化设计时应充分考虑这两个因素的影响.

4) 边腹板倾角对腹板剪力分配影响不大，随着边腹板倾角的增大，边腹板承担的剪力逐渐减小，中间腹板承担的剪力随之增多.