高速铁路桥梁桩基固结蠕变沉降计算方法研究

周涛，徐方，杨奇，吴亚飞

(1. 中南大学 土木工程学院，湖南 长沙410075；2. 林同棪国际(中国)工程咨询有限公司，重庆401121；3. 中南大学 高速铁路建造技术国家工程试验室，湖南 长沙410075)

高速铁路速度快、安全性高、舒适度高和连续运营的特点，要求轨道结构持久稳定的平顺性，这对线下基础工后沉降的控制提出了十分严格的要求[1]。为了控制高速铁路桥梁工后沉降和提高承载性能，桥梁基础一般采用桩基础，因此桩基工后沉降控制成为了高速铁路桥梁设计和施工的关键技术之一，而桩基工后沉降构成主要是固结和蠕变沉降[2−3]。桩基现有沉降计算方法主要有：1)经验方法[4−5]；2)基于相互作用系数和叠加原理的方法[6−7]；3) 等效筏(墩)基法[8−9]；4) 有限元和有限差分等数值分析方法[10−11]；5)基于前期实测沉降的经验预测法[12]。上述所提方法主要研究桩基的总沉降，高速铁路铺轨时间的确定、工后沉降控制严格，须考虑桩基固结蠕变的时间效应研究。胡德贵等[13]提出了基于弹性理论预估桩基工后沉降的方法。曾庆有等[14]采用Mesri 蠕变模型描述了桩底土的蠕变行为，建立了一套计算桩基长期沉降的简单实用的方法。程泽海等[15]采用有限元方法研究了桩基的沉降时间效应并进行了参数分析。BOOKER 等[16]采用黏弹性模型模拟土体的蠕变行为，应用Laplace 变换法分析桩基的长期沉降。BROWN 等[17]建立了能考虑不均匀地基土黏弹性特性的蠕变沉降计算方法。GUO[18]推导了在轴向荷载作用下，非线性黏弹性土层中单桩响应的封闭解，研发了计算程序GASPILE，并对单桩的蠕变行为进行了分析。WU 等[19]在考虑桩周土黏弹性和虚拟桩土模型的基础上，提出了分析单桩沉降时间效应的方法。YANG 等[20]提出了可以考虑地基土固结特性和加载时间效应的群桩长期沉降方法，但没有考虑地基土的蠕变特性。BARTOLOMEY等[21]提出了能考虑土体黏弹塑性的桩基长期沉降计算方法。SMALL 等[22]采用三维有限元分析桩筏基础的沉降与时间的关系。EDIL 等[23]开展模型试验获知桩沉降的时间效应主要由于桩土接触面和桩周土的剪切蠕变引起。DANNO 等[24]提出了应用有限元结合有限差分法开展水体耦合分析来预测软土区桩基长期沉降的计算方法。CUI等[25]采用有限元方法研究了桩筏基础的固结沉降特性。FENG等[26]提出了考虑土体蠕变效应的高速铁路桥梁桩基沉降计算方法。高速铁路桥梁基础受荷随着桥墩、梁、混凝土板、轨道板和轨道的施工而不断的增大，实际为一个多级加载过程，荷载的时间效应对长期沉降的预测有很重要的影响，而考虑这一重要影响因素的研究少。鉴于此，本文在改进“桥梁群桩沉降计算三维复合分析方法”[27]和“桥梁桩基长期沉降计算方法”[20]基础上，提出了能模拟高速铁路桥梁桩基实际加载情况和考虑桩端成层土固结蠕变特性的桩基长期沉降计算方法。为提高计算效率和便于工程应用，编写了群桩长期沉降计算分析程序LTPGSⅡ。桥梁桩基沉降的现场实测值与计算结果的对比分析验证了所提方法的有效性和可靠性。

1 高速铁路桥梁桩基受荷历程

铁路桥梁群桩基础一般由刚性承台和若干根单桩构成。通过现场跟踪记录、分析武广[2]、京沪高速铁路典型试验工点桥梁施工过程可知，在承台施工后，桥墩现浇、梁体现浇和轨道结构依次有序施工，每一个施工步中，可以近似认为作用在桥梁桩基的荷载线性增加，最后铺轨，恒载基本稳定。考虑到更一般的情况，可将铁路桥梁桩基的受荷历程简化成多级阶梯加载，典型的荷载(P)-时间(t)曲线如图1所示。

1.1 多级阶梯加载函数表达式q(t)

文献[28−29]研究结论可知：作用在桩端土顶面的荷载随时间增加规律与作用在桩基顶荷载随时间增加规律是一致的，因此桩端土顶面所受荷载与时间关系曲线也为多级阶梯加载，如图2 所示。阶梯加载的分段函数q(t)可由式(1)表示：

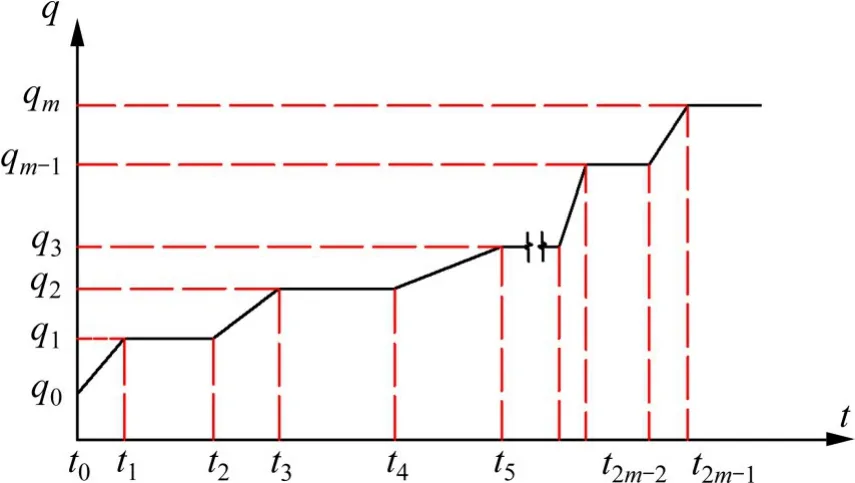
图2 桩端土顶面荷载−时间(q-t)关系曲线示意图Fig.2 Pressure on supporting layers below pile ends

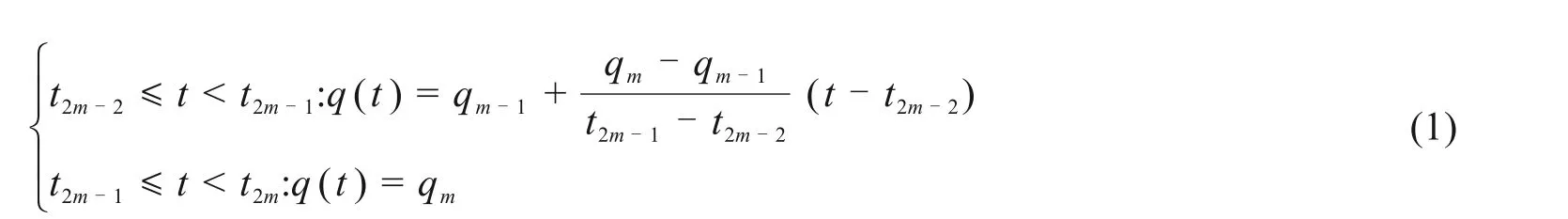
1.2 荷载q(t)函数的Laplace变换

q(t)的Laplace变换公式如下：

式中：s为Laplace变换参数。

式(1)中各时间段q(t)代入式(2)可得：

2 多层黏弹性地基的一维固结分析模型

多层饱和黏弹性地基土一维固结问题计算示意如图3，其中ki为第i层土的渗透系数；E0i，E1i，K0i和K1i为如图所示Schiffman 流变模型[30]的4 个模型参数；q(t)为外加荷载；hi为土层表面到第i层底面的深度，地基表面透水，底层透水或不透水。

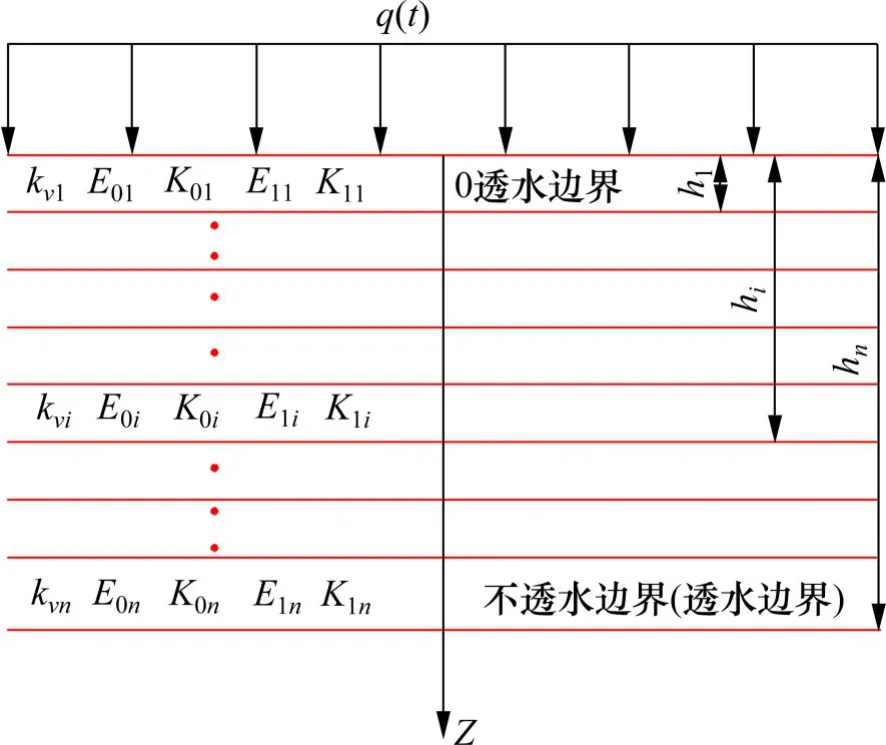
图3 多层黏弹性地基一维固结计算模型示意图Fig.3 Analysis model of layered viscoelastic soils

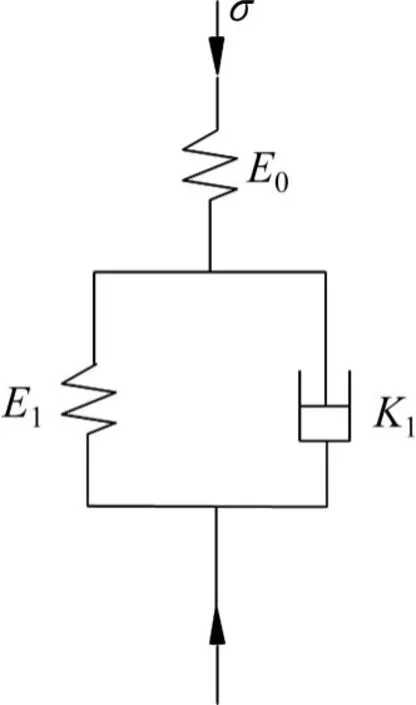
图4 Schiffman蠕变模型Fig.4 Diagram of the Schiffman model

2.1 黏弹性地基固结控制方程

Schiffman流变方程[30]为

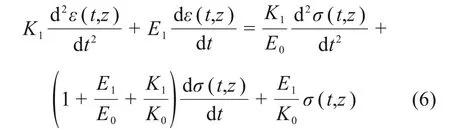
式中：σ(t,z)和ε(t,z)分别为z深度处t时刻土单元体竖直有效应力(增量)和竖向应变。当σ(z,t)已知，通过式(7)获得ε(z,t)：

式中：τ为时间。

Terzaghi一维固结理论方程[30]为：

式中：γw为水的重度；kv为竖向渗透系数；u(t,z)为超孔隙水压力。有效应力原理为

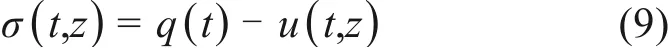
式(8)～(9)代入式(6)整理可得

对于第i层土，令和，代入式(10)整理得控制方程：

对控制方程(11)进行Laplace变换得

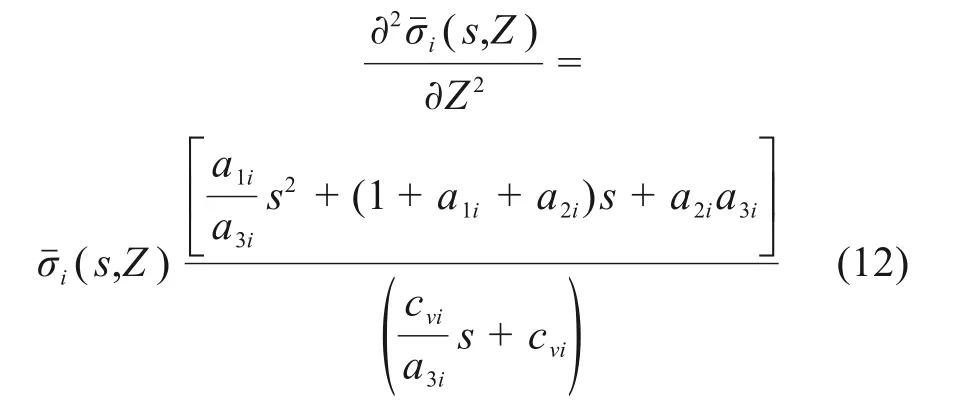
2.2 方程的求解

控制方程(12)求解过程如下。

初始条件：

层间应力连续条件：

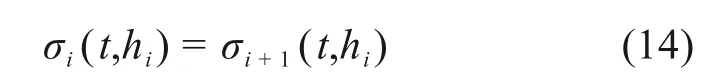
层间流量连续条件：

边界条件I：顶面透水，底面不透，

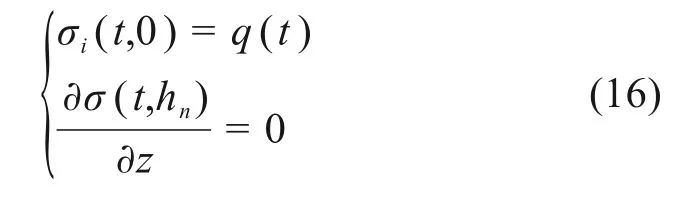
边界条件Ⅱ：顶面透水，底面透水，

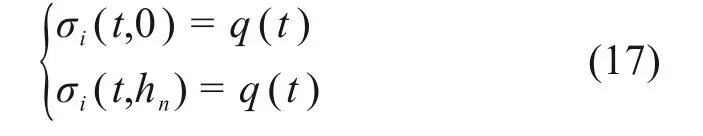
联合初始条件式(13)，可得方程(12)的解如下：

式中：A1,i，A2,i为待求参数。

式(18)分别代入连续性条件式(14)～(15)的La‐place变化式可得：

根据式(20)～(21)，系数矩阵[Di]和[Mi]可分别定义为

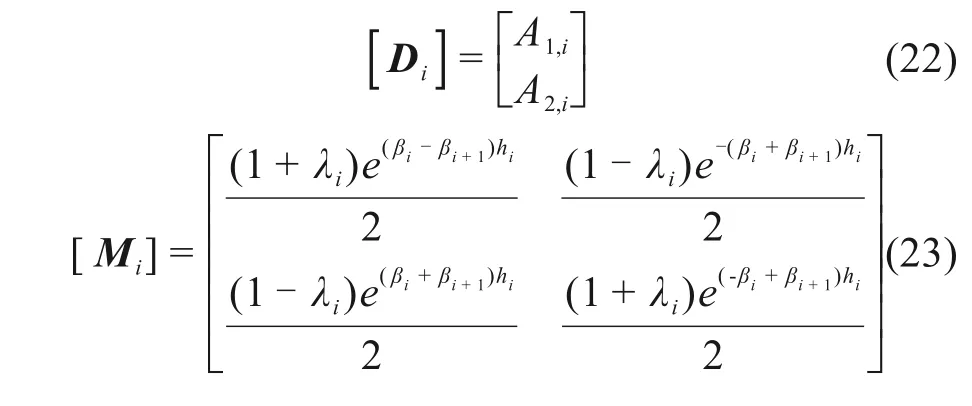
式中：λi=ki βi/ki+1βi+1。

利用系数矩阵[Di]和[Mi]，式[Di+1]可用矩阵形式重新表示为

基于此式(24)，式(18)可用矩阵形式重新表示为

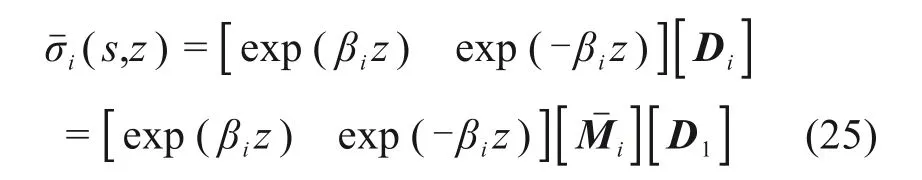
式(25)分别代入边界条件式(16)～(17)的La‐place变化式可得：

边界条件I，

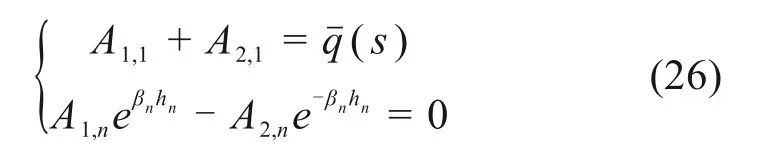
边界条件Ⅱ，

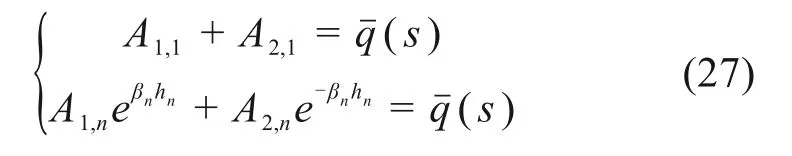
采用矩阵的形式，边界条件式(26～27)的La‐place变换式分别表示为

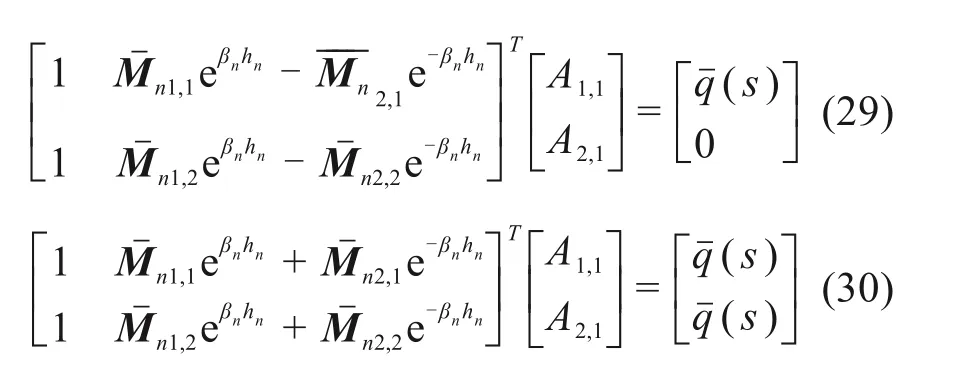
分别求解方程(29～30)，可获得边界条件I 和II系数条件下的系数矩阵

边界条件Ⅰ，

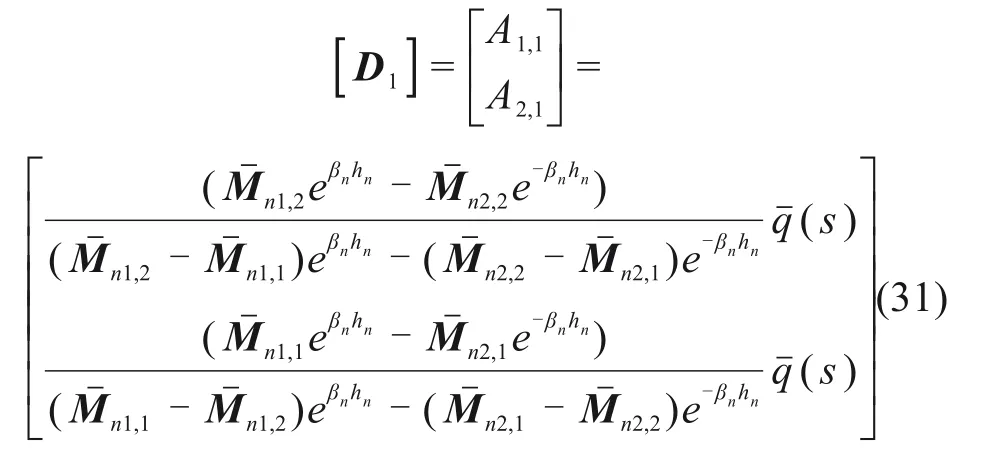
边界条件II,

[D1]代入式(24)得系数矩阵[Di]，再代入式(25)即可求得第i层黏弹性地基土有效应力的拉氏变换解(s,z)。对式(25)进行Laplace 逆变化，由留数定理计算反演积分得竖向有效应力的时域积分形式解为

对于简单σˉi(s,z)情况下，可以直接应用式(33)进行逆变换得解析解，但在复杂的情况是很难算出，这时只能用数值反演的方法来求其反演近似值。本文采用Stehfest 法[33]求解深度z处t时刻的有效应力，Stehfest法Laplace逆变换数值反演计算公式如下：

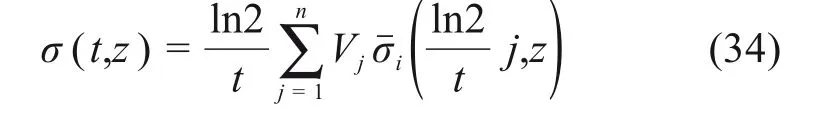
3 桥梁桩基的固结蠕变沉降

当第i层土竖向有效应力σi(t,z)已知，基于式(7)得第i层土竖向应变εi(t,z)，积分可得第i层土的压缩量为：

按分层总和法计算桩底土的总压缩量Ss(t)

加上桩身的压缩量Sp(t)，桩基t时刻的总沉降S(t)为

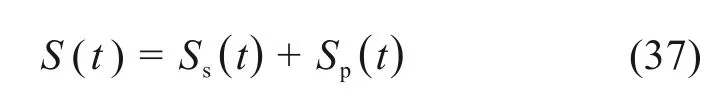
桥墩群桩基础实际上是一个空间问题，要充分考虑桩间距、桩数、桩的平面布置及方向等因素对桩基础的沉降特性的影响，若采用一维或二维的分析方法，则很难反映实际的情况。冷伍明等[27]提出了“桥梁桩基三维复合分析方法”，其把桩底压缩层的分层总和法与承台-桩-地基土共同作用的三维分析矩阵结合起来，可以考虑桩土相互作用的三维特征和计算桩基的内力和变形。此方法主要是把桩基的变形计算分作2 个部分：第1部分计算的是承台与桩体的压缩变形；第2部分计算的是桩底压缩层的压缩变形。本文是在“三维复合分析方法”基础上，对其进行改进使得本文方法能模拟桩基实际的加载情况和桩底成层土的固结蠕变特性。为了提高计算的效率和精度，研制了群桩长期沉降分析计算程序第2版Program for analysis of the long-term settlement of the pile groups，简称LTPGSⅡ，程序流程如图5所示。

图5 LTPGSⅡ程序流程图Fig.5 Flowchart of the LTPGSⅡprogram

4 工程计算实例

4.1 工程概况

试验工点位于上海市华漕镇的京沪高速铁路蕴藻浜特大桥32 号桥墩，基础采用群桩3×7=21 根钻孔灌注桩，桩径1.0 m，桩长73 m，承台尺寸为23.1 m(长)×8.5 m(宽)×2 m(高)。单桩竖向容许承载力设计值为4 664.3 kN。采用单点沉降计对桩基的长期沉降进行观测，桥墩桩基立面和平面图分别如图6(a)～6(b)所示。32 号墩位处各土层分布见图6(a)，土层基本物理状态和力学性质指标如表1所示。

图6 32号墩桩基础图Fig.6 Pile foundation of pier No.32

4.2 现场桩基受荷情况

试验工点32 号桥墩基础为京沪线和沪宁联络线共用，桩基础具体受荷过程可分以下4 个加载步：墩身、立柱浇筑；沪宁联络线连续梁浇筑；京沪线简支梁浇筑和沪宁联络线轨道工程的铺设；京沪线轨道工程的铺设。各阶段荷载及对应时间见表2，受荷可简化为阶梯分级加载，具体荷载-时间曲线关系如图7所示。

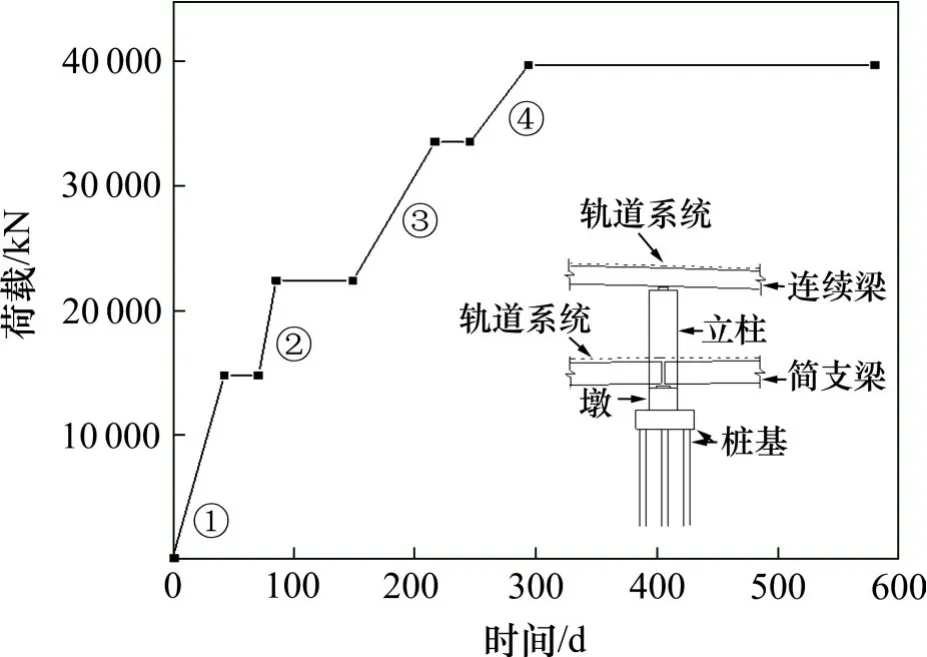
图7 32号墩桩基受荷历程曲线Fig.7 Loading history of the pile foundation of pier No.32

表2 桩基受荷-时间关系Table 2 Relationship of Load-time on the pile foundation

4.3 计算分析结果

采用高压固结仪开展桩底土层的蠕变试验，获得Schiffman 蠕变模型所需参数E0，E1，K0，K1和kv的取值如表3所示。

表3 土层Schiffman 模型的参数Table 3 Values of soil parameters in the Schiffman model

基于上述提供桩基尺寸，地层参数和荷载等条件，利用程序LTPGSⅡ，计算分析获得了32 号墩桩基荷载−沉降−时间关系，并与现场观测结果[20,28]进行对比，结果如图8 所示。分析图8 可知：1)计算得到桩基沉降S(t)曲线与荷载时程曲线一样呈现“阶梯状”，表明桩基受荷历程对其沉降发展规律影响显著。计算沉降随时间的发展规律和实测沉降规律吻合较好，沉降值随时间而增加，铺轨完毕后，沉降渐趋于稳定。2) 考虑桩底土固结蠕变特性的沉降值大于只考虑桩底土固结特性的沉降值，但二者的差别有限，说明桩底土的蠕变变形不明显。

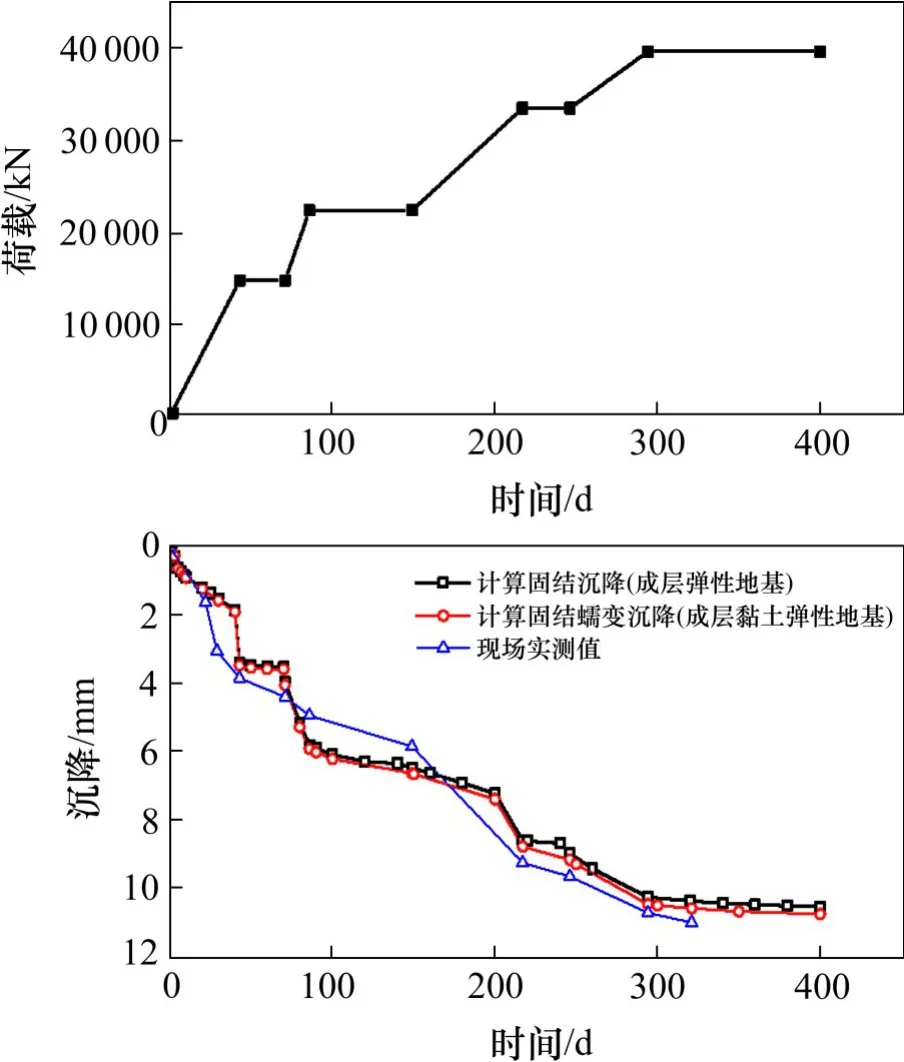
图8 32号墩桩基计算沉降和现场观测沉降对比Fig.8 Comparison of calculated and measured settlementtime curves

5 结论

1)建立了多级加载作用下单面(双面)透水边界多层黏弹性地基一维固结方程，推导了桩底压缩层在多级加载作用下有效应力和沉降的计算公式。

2) 提出了可考虑高速铁路桥梁桩基实际加载情况和桩底压缩层固结蠕变特性的长期沉降计算方法。

3) 试验工点桥梁桩基沉降计算结果与实测对比分析表明，计算获得的长期沉降发展规律和实测沉降有较好一致性，验证了所提桩基长期沉降计算方法的正确性和程序LTPGSⅡ的可靠性。