列车荷载在双块式无砟轨道中静态传递特征研究

张鲁顺，禹雷，赵磊，刘钰

(1. 中铁工程设计咨询集团有限公司 轨道工程设计研究院，北京100055；2. 中国铁道科学研究院集团有限公司 铁道建筑研究所，北京100081；3. 西南交通大学 土木工程学院，四川 成都610031)

2020 年国铁集团出台《新时代交通强国铁路先行规划纲要》，提出到2035年，全国铁路网将达到20 万公里左右，其中高速铁路7 万公里左右。如此规模庞大的铁路网在运营过程中，荷载效应会引起结构疲劳损伤及稳定性等问题[1]。列车荷载是作用在无砟轨道上的主要荷载，通过钢轨和扣件系统传递到无砟轨道主体结构，并在无砟轨道内部传递及重新分配，使轨道结构发挥其承载、传载的功能。因此，对于列车荷载在轨道结构中传递规律的研究是无砟轨道荷载取值的基准，也是无砟轨道材料及几何尺寸优化的重要依据之一。轨道结构的研究往往以问题为导向展开，有砟轨道结构在列车荷载作用下稳定性及伤损问题较多，对其荷载效应较为重视，特别是普速铁路路基标准相对较低，翻浆冒泥发生的比例较大，路基内荷载传递研究成果就比较多。其中，列车荷载在散体道床中传递规律方面，已经提出了散体道床荷载传递基本图式以及不同部件受力特征与控制标准，形成了以道床下沉、轨道破坏系数、不平顺收敛理论和轨道部件受力为基本内容的轨道破坏理论及控制标准[2−4]，压应力在道床中传递扩散角度取值为35°～45°。列车荷载在路基中传递规律方面，在现场实测和理论计算方面开展了较多的分析研究，路基设计荷载简化为纵向三角形，横向均匀分布模式，且动应力在路基内的扩散角度取45°[5]。另外，路基动应力及动变形沿路基深度的变化规律研究较多[6−9]，这就为高速铁路路基结构分层及控制标准的制定提供了依据。列车荷载在无砟轨道中传递规律的研究，大多集中在车辆荷载从钢轨传递至扣件及振动特性传递方面[10−12]，荷载在无砟轨道主体结构中的传递研究较少，一般沿袭有砟轨道研究思路或取无砟轨道各结构层表面最大压应力值的10%为有效荷载区域，得到车辆荷载在无砟轨道中的应力扩散角度为45°左右。为得到列车荷载在无砟轨道中精准的传递规律，本文建立了双块式无砟轨道列车荷载传递规律精细化分析模型，对列车荷载在道床板和支承层内的传递规律以及主要影响因素进行分析。

1 车辆荷载传递模型的建立

1.1 计算模型及参数

路基上双块式无砟轨道荷载传递计算模型如图1 所示，模型纵向长13 m，横向对称简化计算，纵向为连续结构，采用对称边界条件。双块式无砟轨道由钢轨、扣件系统、道床板和支承层等组成，为纵向连续配筋混凝土结构。其中，道床板采用C40 混凝土现场浇注，支承层为HGT 水硬性材料，相关参数见表1。道床板与支承层均采用二次实体单元模拟，提高了荷载传递路径的精准性，路基垂向刚度取76 MPa/m，支承层与路基间的摩擦因数为0.5。列车荷载按照《高速铁路设计规范》中推荐取单轮单侧100 kN。

表1 双块式无砟轨道计算参数Table 1 Parameters of double-block ballastless track

图1 双块式无砟轨道列车荷载传递分析模型Fig.1 Analysis model of train load transfer on double-block ballastless track

1.2 模型合理性验证

为验证列车荷载传递模型的合理性及研究双块式无砟轨道内部荷载传递规律，在高速铁路轨道技术国家重点实验室内建立5.8 m 双块式无砟轨道实尺模型，应用石基压电传感测试系统及扣件支反力测力垫板，对钢轨经由扣件传递至无砟轨道表面的扣件支点压力分布规律、无砟轨道内部荷载传递规律进行了系统性测试，荷载传递测试现场如图2。为与实尺试验相对应，加载量值取100 kN，单侧50 kN，将列车荷载传递模型理论计算结果与实尺模型试验结果对比，如图3～5所示。可见理论计算结果与试验结果变化规律相似，数值差异较小，验证了车辆荷载传递模型的合理性和准确性。

图2 列车荷载传递测试现场Fig.2 Train load transfer test on site

图3 钢轨支点压力分布Fig.3 Pressure distribution diagram of rail fulcrum

图4 道床板底部压应力横向分布Fig.4 Horizontal distribution of compressive stress at the bottom of the track bed

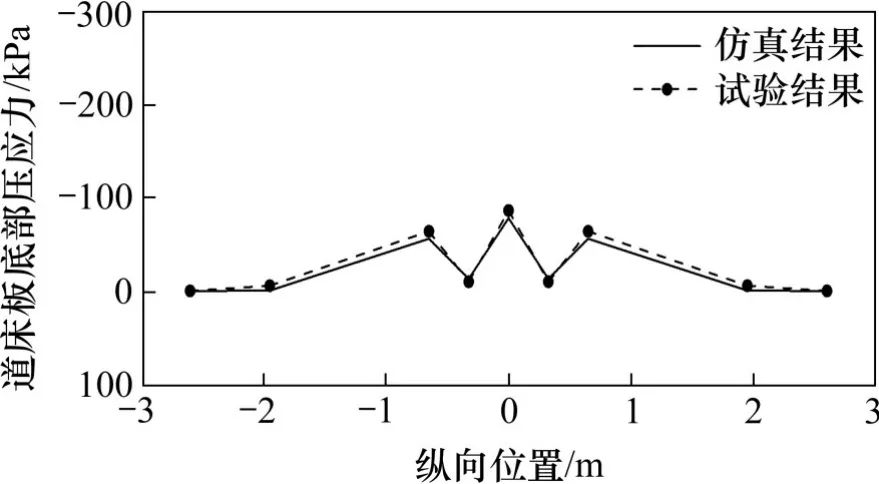
图5 道床板底部压应力纵向分布Fig.5 Longitudinal distribution of compressive stress at the bottom of the track bed

2 列车荷载传递路径分析

荷载传递国内外多以应力作为评价指标，考虑到荷载传递时，应变是一个直接量，而应力是一个间接量，为此，本文通过竖向应变分析荷载传递路径分布。通过计算得出轨道板最大竖向应变约为40 με，取其95%，即竖向应变量大于2 με的范围作为列车荷载有效传递区域。

2.1 荷载传递横向分布规律

无砟轨道轮载主要由中间5对扣件承担，轮载直接作用处扣件为扣件i，与其相邻的2 个扣件分别为扣件i-1 和扣件i-2。轮载作用下轨道结构竖向应变在不同位置扣件处横向分布云图如图6 所示。轮载扩散角取道床板顶部与底部轮载分布边界连线与垂向夹角。扣件i 处，道床板内轮载以扩散角22°向下传递，道床板底部横向影响范围为443 mm，横向2 钢轨间无叠加；支承层内荷载分布范围迅速扩展至无砟轨道横向边界。可以将轮载传递过程分为上下2 部分，上面部分为荷载扩展区，主要分布在道床板内；下面部分为荷载均化区，主要分布在支承层内。扣件i-1 处，道床板内轮载以扩散角15°向下传递，道床板底部横向影响范围为355 mm，由于扣件轮载分配率由中间往外逐渐减少，荷载传递范围也随之减小，因此，荷载量值对荷载传递路径影响显著。总体来看，轮载在道床板内分布范围较小，分布范围的面积越小，承受的荷载越集中，分布范围的面积越大，荷载分布越均匀。从荷载传递的角度考虑，道床板宽度有一定的优化空间，但从振动特性的角度考虑，道床板宽度越大越好，轨道板尺寸优化时需综合考虑荷载分布范围和轨道振动特性2方面因素。另外，车辆荷载在道床板内的扩散角较有砟轨道明显减小，这是由于无砟轨道刚度和有砟轨道存在差异，无砟轨道刚度较大，荷载传递较为集中，扩散角较小。

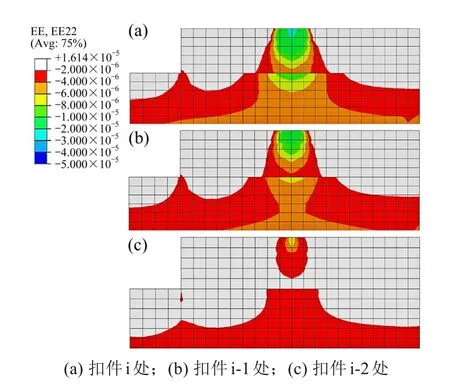
图6 不同位置扣件处荷载传递横向分布云图Fig.6 Cloud diagram of load transfer lateral distribution at different positions of fasteners

图7为不同位置扣件对应的承轨台中心处竖向应变随无砟轨道深度变化规律。可以看出，竖向应变在无砟轨道深度0.1 m 范围内快速衰减，扣件i，扣件i-1 和扣件i-2，在此范围内分别衰减72%，76%和79%。荷载继续向下传递，应变量值逐步稳定。由于道床板与支承层尺寸的差异，在2层交界面位置处，荷载作用产生一定程度的突变，竖向应变也相应产生4 με 范围内的突变。因此，道床板顶0.1 m 深度范围内是轨道结构主要承载区域，层间交界处可能因应变量值突变产生疲劳损伤。

图7 不同位置扣件处竖向应变随无砟轨道深度变化规律Fig.7 Variation of vertical strain at different positions of fasteners with depth of ballastless track

图8 为扣件i 处无砟轨道结构层界面位置应变量值横向分布规律。随着荷载向下传递，承轨台下道床板顶部应变峰值明显，传递到支承层底部时应变峰值与承轨台范围外的应变量值差异较小，其荷载分布已较为均匀。由于支承层为低弹模材料，支承层底部整体应变量值较道床板底部大。同时可以看出，轮载作用下无砟轨道结构内横向2扣件间叠加影响不明显。

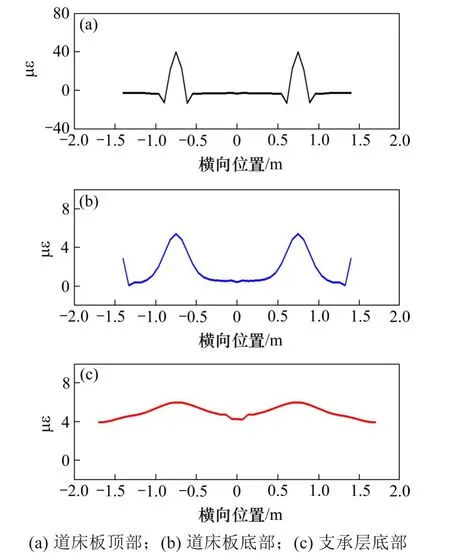
图8 无砟轨道结构层应变量值横向分布规律Fig.8 Lateral distribution law of strain value of ballastless track structure

2.2 荷载传递纵向分布规律

轮载作用下轨道结构竖向应变纵向分布云图如图9 所示。可以看出，轮载纵向主要由5 对扣件承担，所以扣件i-3 位置处分配约为5 kN 的轮载对轨道结构受力影响较小。上部荷载扩展区呈梯形分布，主要在道床板范围内，扣件间无叠加。扣件i 处荷载扩展角为20°，道床板底部纵向影响范围为463 mm；扣件i-1 处荷载扩展角为12°，道床板底纵向影响范围为374 mm。下部荷载均化区在支承层底部影响范围为3 406 mm。

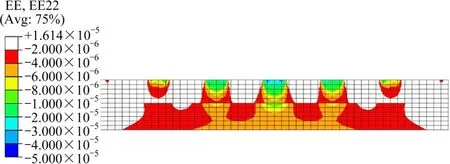
图9 荷载传递纵向分布云图Fig.9 Cloud diagram of longitudinal distribution of load transfer

图10 为无砟轨道结构层界面处应变量值纵向分布规律。可以看出，与横向分布规律类似，承轨台下道床板顶部应变峰值明显，传递到支承层底部时应变峰值均化为单峰值，荷载分布已较为均匀，荷载自上而下其影响范围逐渐扩大。竖向应变量值随无砟轨道深度变化规律取承轨台中心处，因此，纵横向压应变量值随无砟轨道深度变化规律相同，如图7所示。轮载在道床板内分布较为集中，支承层也处于受力范围内，应同时重视道床板和支承层的设计和施工质量控制。

图10 无砟轨道结构层应变量值纵向分布规律Fig.10 Longitudinal distribution law of strain value of ballastless track structure

3 列车荷载传递规律影响因素分析

3.1 动力系数的影响

通过轮载纵横向传递规律可以看出，荷载量值对荷载传递路径有较大影响，在无砟轨道设计计算时，一般需要考虑动力系数的影响。《高速铁路设计规范》中推荐轮载取单轮单侧100 kN，经常作用轮载取静轮载的1.5 倍，设计轮载取静轮载的3 倍，为此，计算分析动力系数分别为1.0，1.5和3.0的情况。

图11 为扣件i 处3 种动力系数时荷载传递横向分布云图。荷载扩展区3种动力系数下荷载扩散角分别为22°，31°和42°，道床板底横向影响范围分别为443，547 和759 mm。在荷载均化区内，荷载分布范围逐渐增大，横向影响范围均到达支承层边界，动力系数为1 时，均化区应变云图以2～6 με 为主，动力系数为3 时，均化区应变云图以8～20 με为主，应变云图量值显著增大。

图11 不同动力系数时荷载传递横向分布云图Fig.11 Cloud diagram of lateral distribution of load transfer under different dynamic coefficients

图12 为3 种动力系数下荷载传递纵向分布云图。扣件i 处荷载扩展区内，3 种动力系数下荷载扩散角分别为20°，33°和40°，道床板底纵向影响范围分别为463，614 和超过650 mm，动力系数3.0 时纵向叠加。在荷载均化区内，3 种动力系数下支承层底部纵向影响范围分别为3 406，4 048和4 862 mm。

图12 不同动力系数时荷载传递纵向分布云图Fig.12 Cloud diagram of longitudinal distribution of load transfer under different dynamic coefficients

扣件i 对应的承轨台中心处3 种动力系数竖向应变随无砟轨道深度变化规律如图13 所示。可以看出，动力系数对竖向应变量值影响较大，随动力系数的增加而增大，动力系数为1.5 和3.0 时竖向压应变随轨道深度变化量值分别是动力系数为1.0 时的1.5 和3.0 倍，荷载直接作用处竖向压应变与荷载量值成正比。因此，荷载传递纵横向分布范围及应变量值均随动力系数的增加而显著增大，动力系数为3.0 时，纵向上荷载扩展区内扣件间荷载叠加影响，荷载扩散角与有砟轨道较为接近，轨道结构设计时动力系数应作为主要影响因素考虑在内。

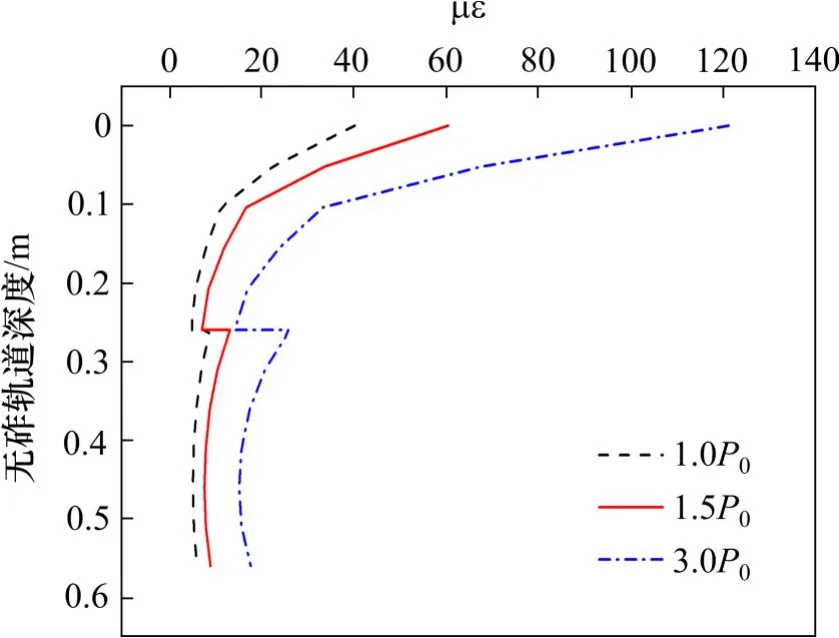
图13 不同动力系数时竖向应变随无砟轨道深度变化规律Fig.13 Variation of vertical strain with depth of ballastlesstrack under different dynamic coefficients

3.2 混凝土强度等级的影响

无砟轨道运营过程中，混凝土结构疲劳裂缝等原因会引起强度等级降低，荷载传递路径会有所不同。本节主要对荷载在不同强度等级混凝土内传递路径进行对比。假定道床板混凝土强度等级分别为C30，C40和C60。

图14 为3 种道床板混凝土强度等级时荷载传递横向分布云图。扣件i 位置处，荷载扩展区内，3 种混凝土强度等级下荷载扩散角分别为23°，22°和21°，道床板底横向分布范围分别为452，443和430 mm。扩散角度和分布范围均随混凝土强度等级的增加而减小。在荷载均化区内，横向影响宽度均到支承层边界处。

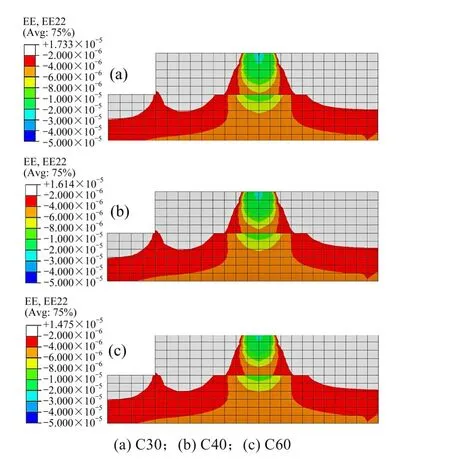
图14 不同混凝土强度时荷载传递横向分布云图Fig.14 Cloud diagram of lateral distribution of load transfer at different concrete strengths

图15 为3 种混凝土强度等级下荷载传递纵向分布云图。扣件i 位置处，荷载扩展区内，3 种混凝土强度等级下荷载扩散角分别为21°，20°和19°，道床板底纵向分布范围分别为470，463 和450 mm，分布规律与横向分布类似。在荷载均化区内，3 种混凝土强度等级下支承层底部纵向影响范围分别为3 408，3 406和3 405 mm。可见，无砟轨道材料弹性模量越大，抵抗车辆荷载变形所需的范围就越小，而有砟轨道离散性大，承受荷载需要较大的范围。因此，也可说明无砟轨道应力扩散角度低于有砟轨道。

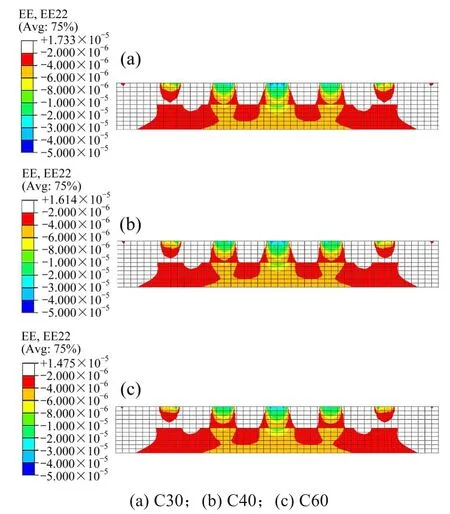
图15 不同混凝土强度时荷载传递纵向分布云图Fig.15 Cloud diagram of longitudinal distribution of load transfer at different concrete strengths

3 种道床板混凝土强度等级下竖向应变随无砟轨道深度变化规律如图16 所示。道床板内随着混凝土强度等级的增加，竖向应变量减小。荷载传递至支承层内时，支承层内混凝土强度等级不变，竖向应变量相差较小，且道床板与支承层强度等级差别越大，层间压应变突变程度增大。因此，混凝土强度等级对荷载传递路径和量值都有一定程度的影响，随着混凝土强度等级的增加，荷载扩展区纵横向承载范围减小，单位体积的混凝土能承受更多的荷载且应变量减小，有利于提高轨道结构承载性能。

图16 不同混凝土强度时竖向应变随无砟轨道深度变化规律Fig.16 Variation of vertical strain with depth of ballastless track under different concrete strengths

3.3 下部基础刚度的影响

随着无砟轨道应用环境的不同，下部基础刚度变化也各异。路基、桥梁和隧道支承刚度典型值分别为76，1 000 和1 200 MPa/m，为分析下部基础结构形式差异对无砟轨道荷载传递规律的影响，下部基础刚度k选取3个值，分别为76，1 000和1 200 MPa/m。

图17 为3 种基础刚度值下荷载传递横向分布云图。扣件i 位置处，荷载扩展区内，3 种基础刚度下荷载扩散角分别为22°，21°和21°，道床板底横向分布范围分别为443，440 和440 mm。荷载均化区内，除刚度76 MPa/m 时横向影响范围到支承层边界外，其余2种基础刚度下支承层底部影响范围分别为1 598 mm和1 550 mm。

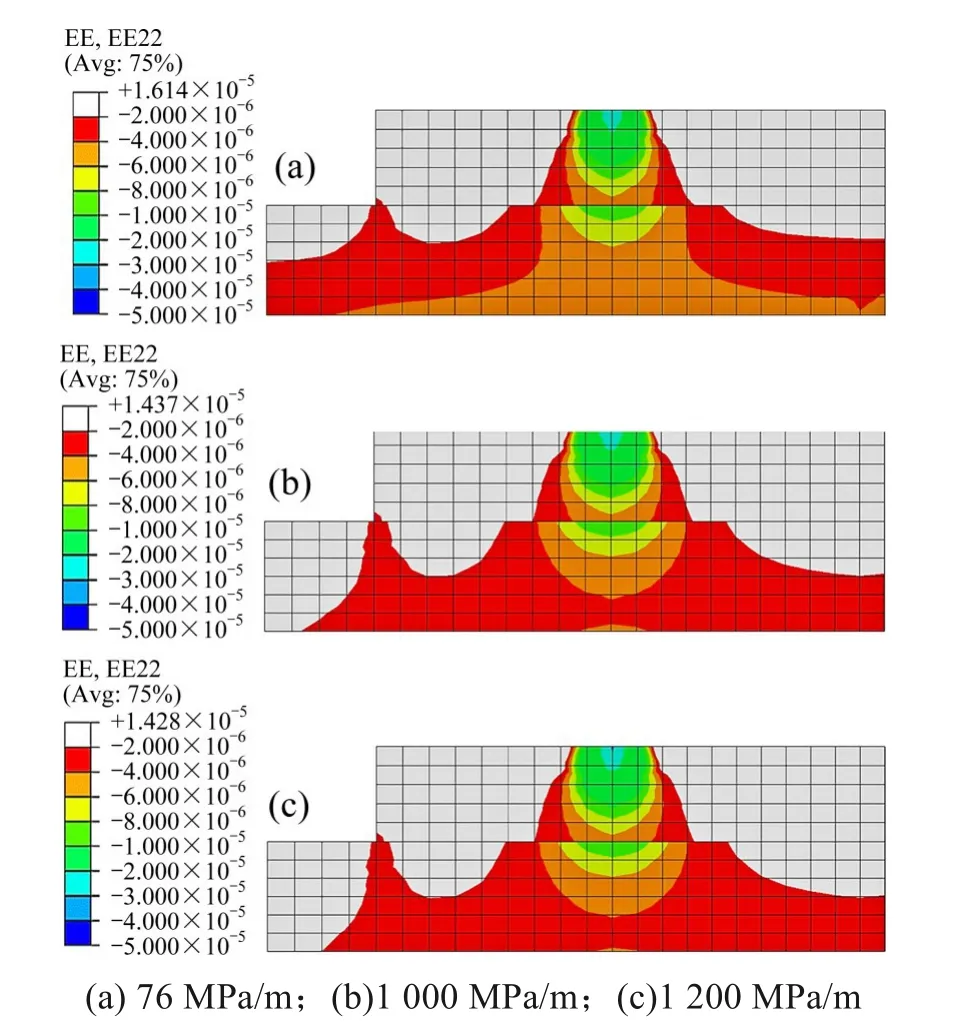
图17 不同基础刚度时荷载传递横向分布云图Fig.17 Cloud diagram of lateral distribution of load transfer with different foundation stiffness

图18 为3 种基础刚度值下荷载传递纵向分布云图。扣件i 位置处，荷载扩展区内，3 种动力系数下荷载扩散角分别为20°，19°和19°，纵向道床板底影响宽度分别为468，463 和463 mm，分布规律与横向分布类似。荷载均化区内，3 种基础刚度值下支承层底部纵向分布范围分别为3 406，2 555和2 510 mm。下部基础为桥梁或隧道时，荷载均化区内荷载分布范围较小，支承层承担更集中的荷载。

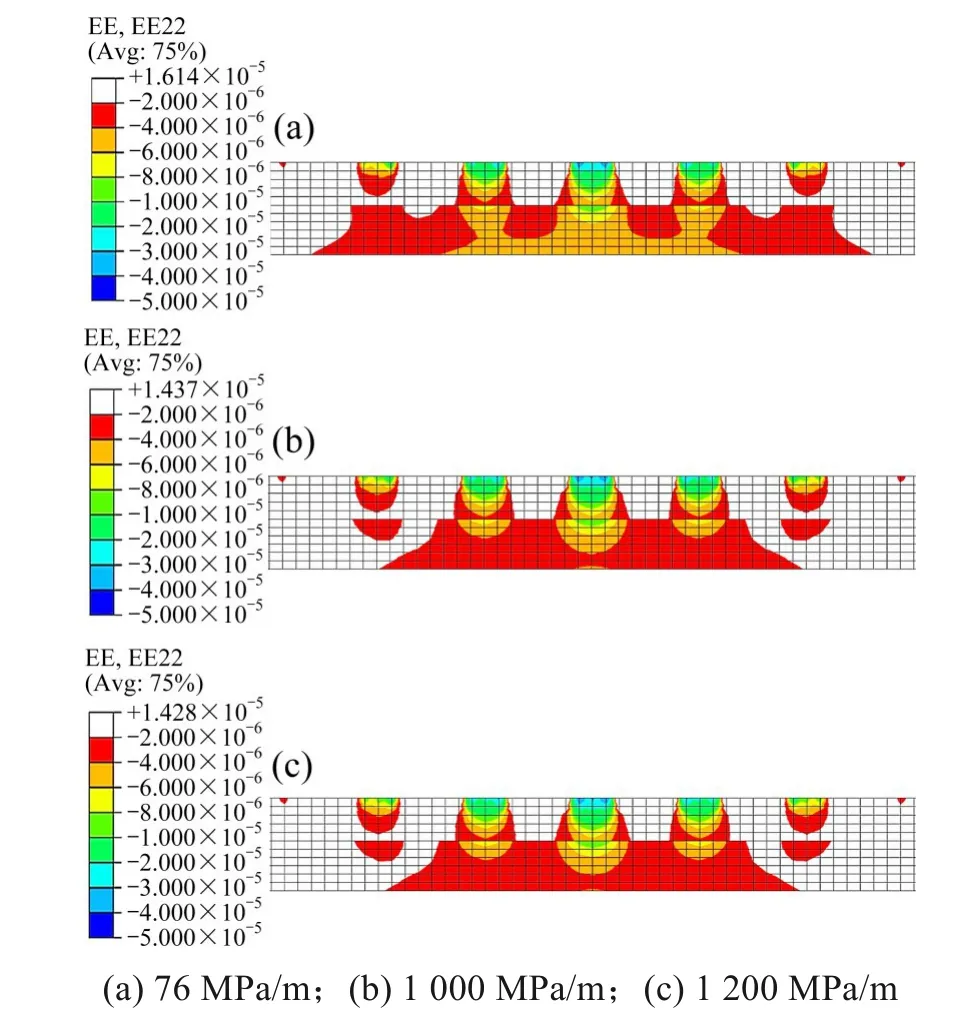
图18 不同基础刚度时荷载传递纵向分布云图Fig.18 Cloud diagram of longitudinal distribution of load transfer with different foundation stiffness

3 种基础刚度值时竖向应变随无砟轨道深度变化规律如图19所示。可以看出，3种基础刚度值时竖向应变量在荷载扩展区差别不大，下部结构为路基时，在支承层底部应变值较桥梁和隧道时大。总体看来，下部基础刚度对应变量值影响较小，而对荷载均化区传递范围影响较大，随着基础刚度增加，均化范围减小。因此，下部基础为桥梁或隧道时，荷载均化区分布范围更加集中，可以适当提高支承层内混凝土强度、优化宽度来提高轨道结构合理性和经济性。

图19 不同基础刚度时竖向应变随无砟轨道深度变化规律Fig.19 Variation of vertical strain with depth of ballastless track under different foundation stiffness

4 结论

1)轮载在无砟轨道结构中的传递分为上下2个部分，上面部分为荷载扩展区，主要在道床板范围内，荷载扩散角度为20°左右；下面部分为荷载均化区，主要在支承层范围内，荷载传递至支承层开始均化，传递至路基面成为均匀荷载。纵向上荷载扩展区扣件间荷载无叠加影响，荷载均化区扣件间荷载叠加成连续区域。列车荷载下道床板受力集中，支承层也处于受力范围内，应同时重视道床板和支承层的设计和施工质量控制。

2) 荷载传递分布范围及应变量值均随动力系数的增加而显著增大，动力系数为1.0，1.5 和3.0时，荷载扩展区扩散角分别为22°，31°和42°，最大应变值分别为40，60 和120 με。动力系数为3.0时，荷载扩展区扣件间荷载叠加影响。

3) 混凝土强度等级对荷载传递路径和应变量值都有一定程度的影响，随着混凝土强度等级的增加，荷载扩展区纵横向承载范围减小，有利于提高轨道结构承载性能。

4) 下部基础刚度对荷载均化区的范围影响较大，下部基础为桥梁或隧道时，荷载均化区分布范围更加集中，可以适当提高支承层内混凝土强度、优化宽度来提高轨道结构合理性和经济性。