基于稀疏成分分析的欠定工作模态参数识别
2021-09-11李海波赖雄鸣陈叶旺
王 鑫,王 成+,李海波,赖雄鸣,陈叶旺
(1.华侨大学 计算机科学与技术学院,福建 厦门 361021;2.厦门市企业互操作与商务智能工程技术研究中心,福建 厦门 361021;3.华侨大学 机电及自动化学院,福建 厦门 361021)
0 引言
模态参数识别是结构健康与结构动力学分析中最重要的工具之一,在过去的几十年中一直是表征和识别线性系统的最佳工具[1-4]。
在近十年中,盲源分离(Blind Source Separation, BSS)技术被越来越多的结构动力学研究人员所关注,并被引入模态参数识别问题中。2007年,PONCELET和ZHOU等[5-7]提出独立分量分析(Independent Component Analysis, ICA)和二阶盲识别(Second Order Blind Identification, SOBI)两种基于BSS的模态识别方法,建立了分离成分和模态参数之间的一对一映射关系,较好地阐述了两种方法应用于模态识别的物理解释。
然而BSS方法只能处理确定与超定下的模态参数识别问题(即观测传感器数大于源信号数),在实际工程应用中,源信号数量通常大于观测传感器数,此时盲源分离为欠定问题,因此对欠定的盲源分离下的模态进行识别具有研究意义。
稀疏成分分析(Sparse Component Analysis, SCA)是解决欠定盲源问题的有效方法,该方法分为混合矩阵的估计和重构源信号两步。不同于ICA,SCA假设源信号在特定转换域内满足稀疏性,稀疏变换的方法[8-11]很多,如短时傅里叶变换、小波变换。稀疏域下的观测信号可以通过聚类方法得到模态振型矩阵,主要的聚类方法[12-17]有K-means聚类、模糊C-均值聚类(Fuzzy C-Means clustering, FCM)、基于密度的噪声应用空间聚类(Density-Based Spatial Clustering of Applications with Noise, DBSCAN)等,近年来的改进聚类算法有郭凌飞等[14]的改进FCM算法、王飞宇等[15]的密度峰值聚类算法、GUAN等[8]的差分进化的K-means聚类算法。在重构信号时,BOYD等[17]利用l1范数最小优化算法求最稀疏解,YONG等[12]采用l0数最小优化算法恢复源信号。然而,以上文献均未涉及欠定状态下模态振型的特性问题。
本文对欠定状态下的模态置信准则(Modal Assurance Criterion, MAC)评估方法、稀疏成分分析的模态评估以及模态阵型给出合理解释,并通过数值和实验进行验证,主要贡献如下:①针对传统BSS技术无法解决欠定的问题,建立了基于SCA的工作模态参数识别框架,并与传统BSS技术进行对比;②对欠定工作模态参数识别振型的解释和评价问题提出欠定条件下识别振型的特点以及模态振型评价方法;③对欠定可识别模态数、模态遗漏和虚假模态问题进行讨论并给出解释。
1 基于BSS的工作模态识别
1.1 工作模态参数识别的问题描述
1.1.1 工作模态参数识别理论
在振动力学理论中,ndof自由度(Degrees of freedom, DOF)线性时不变系统的控制方程表示为
(1)
式中:M∈Rndof×ndof,C∈Rndof×ndof,K∈Rndof×ndof分别为质量、阻尼和刚度矩阵;F(t)∈Rndof×T,为外力矢量在T个时刻上的采样样本组成的矩阵。
根据振动理论,对于一般工程结构小阻尼,只要(系统)结构的各阶固有频率不相等,理论上就有ndof个模态,振动位移响应Xdet(t)=[x1(t),…,xi(t),…,xndof(t)]T可以在模态坐标中分解为
(2)
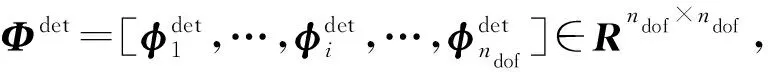
Mr=(Φdet)TMΦdet;
Kr=(Φdet)TKΦdet。
(3)

各阶模态坐标响应qi(t)相互独立,利用单自由度(Single Degree of Freedom, SDOF)识别技术可以很容易地从各阶模态响应qi(t)中识别系统的第i阶固有频率fi和阻尼比ζi。
工作模态参数识别是在没有任何外力矢量F(t)(F(t)∈Rndof×T)先验信息的情况下,仅从位移响应信号中识别模态振型和各阶模态坐标响应,再从各阶模态坐标响应中识别阻尼比和固有频率。
1.1.2 工程中的工作模态参数识别

(4)
根据位移响应传感器个数n与系统自由度和理论模态数ndof之间的关系,有以下3种情况:
(1)为每个自由度布置的振动传感器多于1个,n>ndof,为超定状态。
(2)为每个自由度布置1个振动响应传感器,n=ndof,为正定状态。
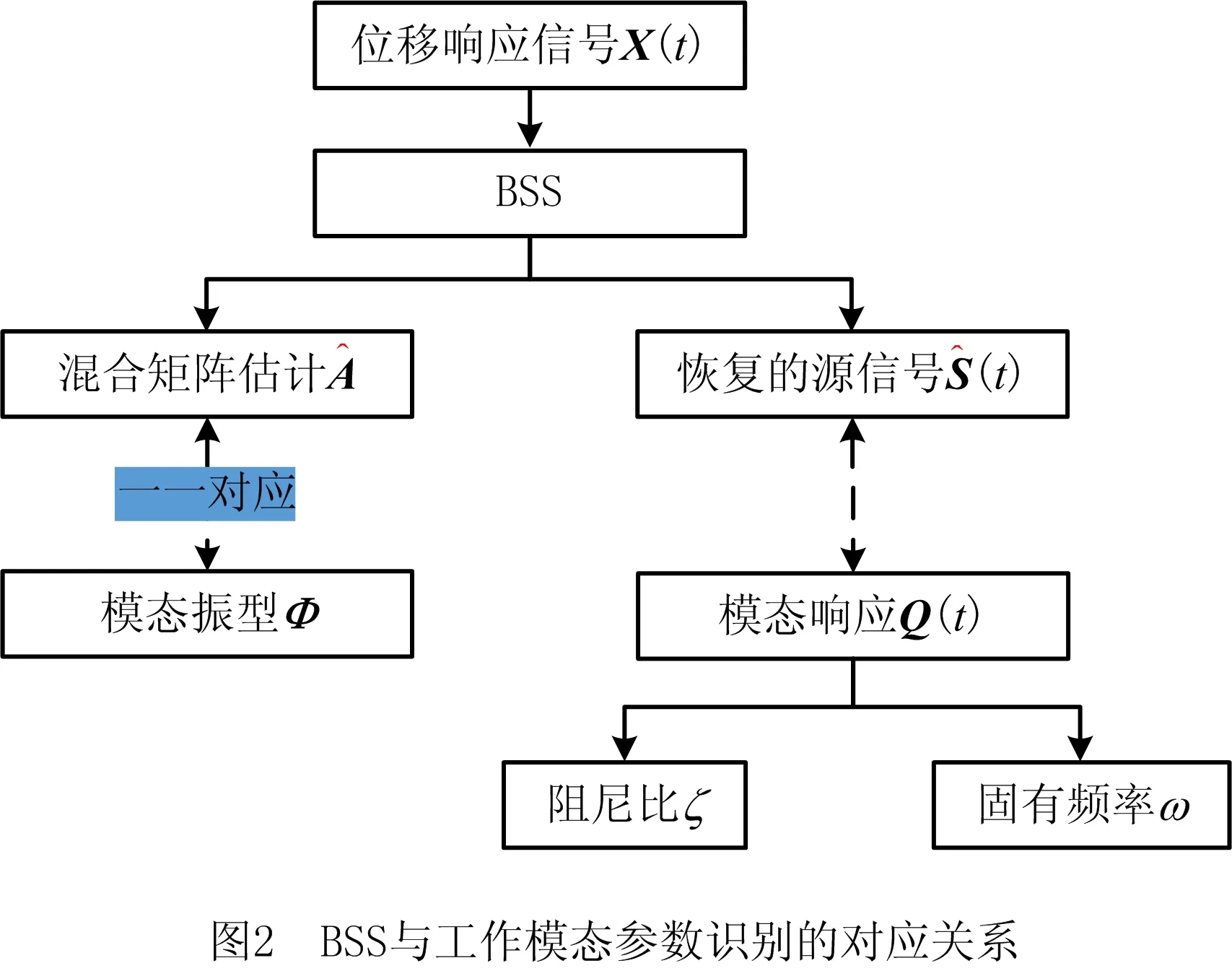
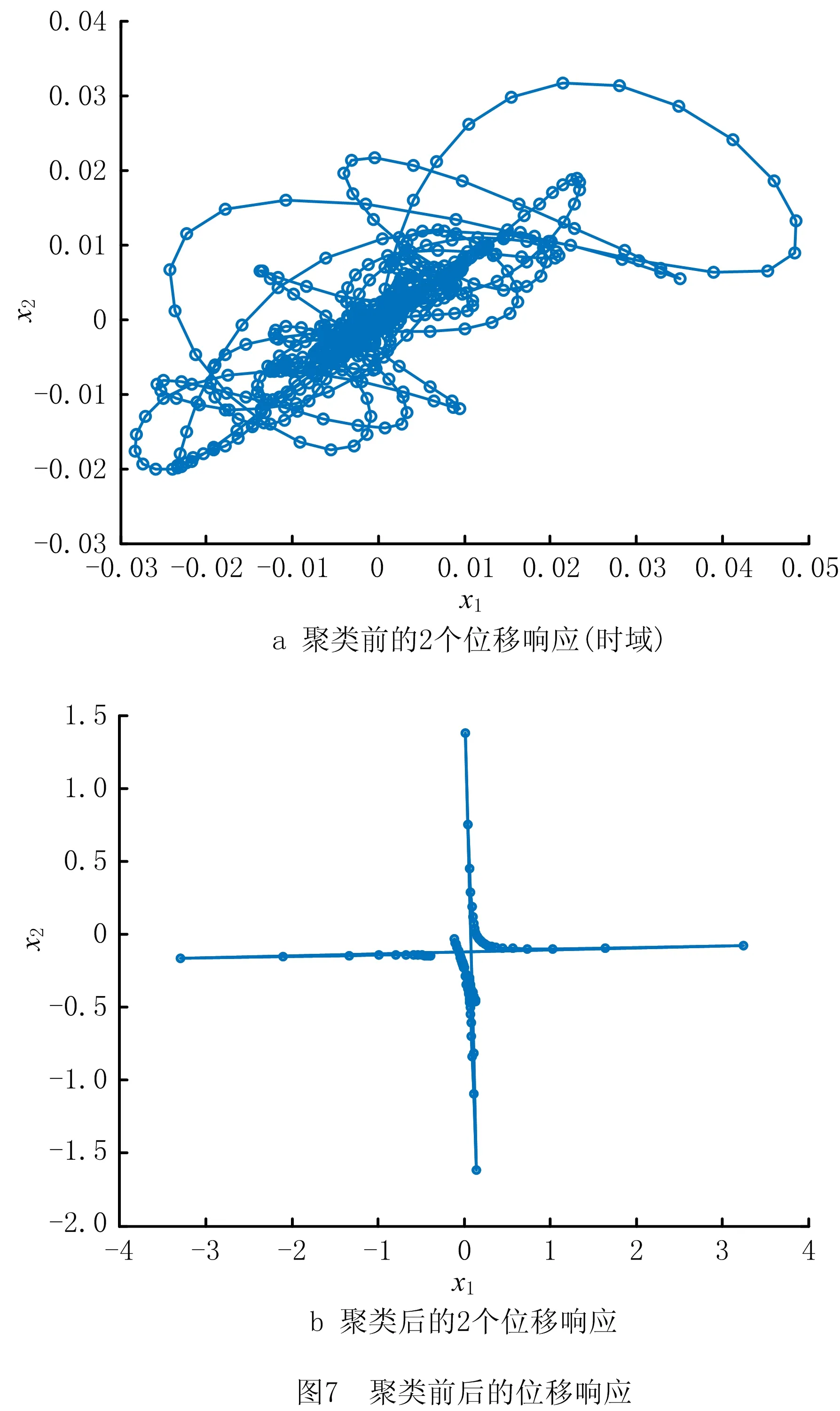
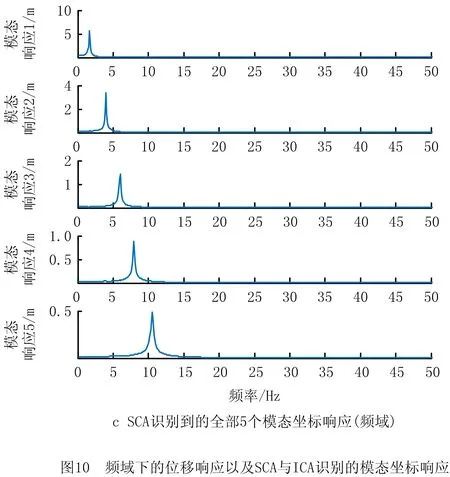
(3)n 实际工程结构一般都是连续体(可视作无限自由度系统,有无限个模态),应用有限元理论,可离散化的自由度个数ndof也较大,而工程中可布置的位移响应传感器输出个数n极为有限,难以为每个自由度布置1个传感器,欠定情况大量存在。 在不考虑噪声的情况下,BSS问题的线性瞬时混合模型如图1所示,可表示为 (5) 图中:S(t)=[s1(t),…,sm(t)]T∈Rm×T,表示输入的m个源信号在T个时刻上的采用样本组成的矩阵;X(t)=[x1(t),…,xn(t)]Τ∈Rn×T,表示n个观测信号在T个时刻上的采用样本;A=[a1(t),…,am(t)]∈Rn×m,为混合矩阵。该模型的含义是m个源信号S(t)经过A混合后得到的n个观测信号X(t)。 (6) 在实际应用下,根据盲信号分离中观测信号数n与源信号数m的不同,有如下3种情况:①n>m,为超定盲源分离;②n=m,为正定盲源分离;③n 式(4)和式(5)的数学表达式有相似之处,而且模态坐标响应矩阵Q(t)和源信号S(t)各分量均相互独立。独立源信号个数m=ndof,工程模态振型矩阵Φ对应混合矩阵A,模态响应向量Q(t)对应源信号的信号矩阵S(t),显然工作模态识别是一个特殊的BSS模型问题,因此可以将BSS技术应用于工作模态参数识别领域,如图2所示。 基于BSS的工作模态识别分为以下3类:①n>m=ndof,为超定状态;②n=m=ndof,为正定状态;③n 在传统的BSS求解方法(如ICA和SOBI)中,分离系统W对应的数学表达式为 (7) SCA提供了解决BSS模型的替代方案,并可解决欠定问题。 放弃独立性假设,SCA假设源信号可以在转换域中稀疏地表示(该转换域称为稀疏域)。基于此,将时域BSS模型线性变换为另一个稀疏ξ域(如傅里叶变换、小波变换[19]等): (8) SCA识别的本质是假设S(ξ)(S(ξ)=[s1(ξ),…,sj(ξ),…,sm(ξ)]Τ∈Cm×T)足够稀疏且不相交,即在某个特定的稀疏域中,ξk∈Ω,最多有一个源向量sj′(ξ)(sj′(ξ)∈CT)是活跃的,且sj(ξ)=0(j=1,…,n),其中j≠j′,则有 (9) SCA涉及混合矩阵估计和实际源信号重建两个主要阶段,其中源信号能否恢复性能很大程度上取决于混合矩阵估计的准确性。基于SCA的欠定BSS流程如图3所示。 首先,通过稀疏变换(如短时傅里叶变换(Short-Time Fourier Transform, STFT))将时域观测信号X(t)转换为稀疏域X(ξ);其次,采用单源点(Single Source Points,SSP)检测算法[20]和聚类算法(如FCM聚类算法、改进的K-means算法)估计混合矩阵;然后,重建稀疏域中的源信号(如采用最小二乘法);最后,通过稀疏变换的逆变换(短时傅里叶逆变换)将稀疏域中的源信号从稀疏域转换到时域。 2.1.1 SSP探测 本节对SSP的原理进行简单介绍。由式(8)可得,当模态响应sj′(ξk)在其转化域非零,即为SSP时,式(9)表示为 X(ξk)=AS(ξk)=aj′sj′(ξk)。 (10) 式(10)两边取实部与虚部,可表示为: Im(X(ξk))=aj′Im(sj′(ξk)); Re(X(ξk))=aj′Re(sj′(ξk))。 (11) 因为观测向量的实部、虚部与混合矩阵中ai向量的方向一致,所以混合矩阵A可以通过聚类技术精确估算。 如果在时间频率中同时激活多个源,则式(11)的实部与虚部可表示为: (12) 因为获得SSP的条件非常苛刻,需要在实际情况下适当放宽条件,所以将稀疏域(如时频域)中实部和虚部绝对方向之差小于给定阈值的点视为SSP[17]。判定为SSP的条件为 Re(X(t,f))ΤIm(X(t,f))/ (13) 2.1.2 聚类 聚类算法是混合矩阵估计的重要组成部分,直接影响其准确性和可行性,同时矩阵估计的质量也会影响源恢复的性能。值得注意的是,每个聚类算法都有其局限性,没有一个能够应对所有应用场景。例如,K-means聚类算法对初始中心选择敏感,容易陷入局部最优解;FCM算法对初始中心选择敏感,收敛速度慢;基于直方图对比(Histogram-based Contrast,HC)显著性算法需要更高的时间复杂度;DBSCAN算法不适用于非均匀数据,超参数的确定对聚类结果影响很大[21-23]。 本文采用FCM算法,步骤如下:①确定分类数的值;②初始化一个隶属度;③根据隶属度计算聚类中心;④计算目标函数;⑤根据聚类中心计算隶属度,返回③,循环直到结束。 SCA利用源信号的稀疏性,从变换的稀疏转换域中的不完整混合信号中恢复源信号。通常恢复源信号的方法是通过求解式(14)找到稀疏解: s.t. X(ξ)=AS(ξ)。 (14) 这种l1最小化技术旨在找到混合信号X(ξ)中的最稀疏解。式(14)是一种信号定义的凸优化问题,其解决方案能够保证全局最优,并可通过线性规划求解方法进行有效地求解。 评估重复模态的判断依据为: (1)识别的频率是否相同 若所识别的两个模态频率相同,则认为识别的是重复模态,否则不是重复模态。该方法不适合密集模态的结构。 (2)两个估计模态振型的MAC值是否接近1 若模态重复,则模态振型的MAC图会出现接近1的很大的数,表示两个不同的模态振型很可能是重复的,为重复模态。 (2)时域采样频率f奈奎斯特采样定理规定,可分析识别频率小于等于时域采样频率f的一半,因此可识别最高阶模态的固有频率小于等于f的一半。 由以上理论分析可知,本文提出的基于SCA工作模态参数识别方法适用于如下情况:①线性时不变小阻尼结构;②要求模态坐标响应Q(t)为稀疏信号;③超定、正定与欠定;④识别的模态振型失去幅值信息;⑤识别结果中仍然可能存在模态遗失和虚假模态等。 与传统BSS技术(如ICA)相比,本文所提基于SCA的欠定工作模态参数识别方法能够在保证识别参数准确的情况下,识别出比传感器数更多阶的模态,如表1所示。 表1 基于SCA和ICA的工作模态参数识别比较 假设系统的自由度为4,采用同样的3个传感器,ICA识别出的模态响应数为3,本文方法最多识别出的模态响应数为4。 (1)实验目的 1)比较基于SCA的工作模态参数识别方法在正定、欠定状态下的模态参数识别效果。 2)欠定状态下,将建立的基于SCA的工作模态参数识别框架与传统BSS技术(如ICA)的模态识别效果进行对比。 3)在不同可识别模态数下,基于SCA的工作模态参数识别方法识别结果中模态遗漏与虚假模态的情况。 (2)实验设计思路 对于目的1),首先模拟出正定、欠定两种情况,并构建基于SCA的工作模态参数识别框架,然后对识别出的模态参数(频率、阻尼比、模态振型)进行评估和比较。 对于目的2),首先构建出欠定状态,实现基于SCA的工作模态参数识别方法与传统BSS方法(ICA方法),然后比较两种方法识别出的模态参数(频率、阻尼比、模态振型)。 对于目的3),将可识别模态数设置成大于、小于、等于自由度数,并评估识别出的模态参数是否存在模态遗漏与虚假模态。 为验证所提方法,采用如图5所示的5自由度质量弹簧阻尼器模型[12]。设质量矩阵M=diag([1 2 2 2 3]),刚度矩阵 K= 5自由度的振动位移观测信号如图6所示。 比较高维空间中两个向量相关性的共同指标为MAC,即 (15) 动力学系统的真实模态参数大致通过3种方式获得:①通过公式推导获得解析解;②有限元仿真;③实验模态分析测定。在不存在错误或严重误差的情况下,3种方法中的任何一种都可以作为理论值的标准来评估工作模态参数识别结果的准确性。本文的理论模态振型是通过方法①和方法②校验一致后得到的结果。 对于虚假模态,比较所识别模态振型的每一列与工程模态振型所有列的MAC值,取其中的最大值作为该振型的模态评估结果。 实验采用窗长为800、步长为4的汉宁窗对观察混合信号进行预处理。ICA采用FastICA方法;SCA设置如下:稀疏变换采用STFT;SSP的值设为2°;聚类算法为FCM;模态响应恢复采用-1最小化技术;采用SDOF识别技术从模态响应信号中识别模态参数。 混合矩阵采用理论的模态振型进行评估,而理论的模态振型φi采用femodal方法生成,该方法的输入为质量矩阵M和刚度矩阵K,输出为固有频率和模态振型。 假设有2个观察信号如图7a所示,稀疏变换前观察信号是混乱的,稀疏变换后会在空间呈现如图7b所示明显的聚类现象,通过聚类方法可以估计出混合矩阵。 4.4.1 正定和欠定状态下的SCA模态参数识别实验 图8所示分别为振动位移响应信号数n=5时识别的时域和频域模态坐标响应。模态参数识别结果对比如表2所示。 表2 使用SCA在正定与欠定下的识别结果 4.4.2 SCA与ICA的对比实验 表3 5自由度下SCA与ICA的对比 4.4.3 可识别模态数、模态遗漏、重复模态与虚假模态的评估实验 表4 3种欠定条件下的MAC值实验结果 表5 SCA的时的识别模态MAC表 由表2可知,确定与欠定下,基于SCA的工作模态参数识别方法识别的模态参数非常接近,而且接近理论值。 由表5所示的实验结果可知,识别出的模态之间的MAC值未出现趋于1的情况,因此没有产生重复模态。 本文首先论述了SCA与工作模态参数识别的对应关系,然后探讨了基于SCA的工作模态参数识别中,3种欠定状态下模态振型范围与模态振型的评价问题,最后经过5自由度下的数值模拟实验表明,模态振型个数小于自由度数时为真实模态振型,超出自由度数的模态为虚假模态振型。 SCA算法的细节对工作模态参数的精度影响很大,本文仅采用经典的SCA方法,其中稀疏变换采用STFT,聚类方法采用FCM,源信号恢复采用-1最小化技术,下一步可以考虑采用最新的稀疏变换、聚类和源信号恢复方法。另外,实验验证仅采用多自由度、结构不变和冲击激励的振动衰减信号仿真数据集,基于SCA的欠定工作模态参数识别方法还需要在工程结构和环境激励更加复杂的实测振动响应数据集上进行验证。1.2 盲源分离基本理论

1.3 基于BSS的工作模态识别及存在的问题

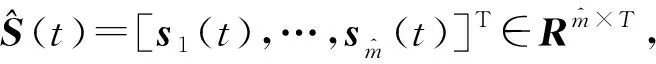
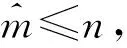
2 稀疏成分分析


2.1 混合矩阵估计


2.2 源的重构
3 基于稀疏成分分析的欠定工作模态参数识别

3.1 稀疏成分分析与工作模态参数的对应关系


3.2 欠定状态下的模态振型评估和特点
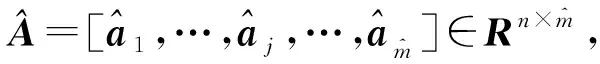
3.3 可识别模态数、模态遗漏、虚假模态与重复模态





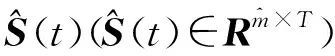
3.4 方法的适用范围
3.5 方法的理论分析和比较

4 仿真验证
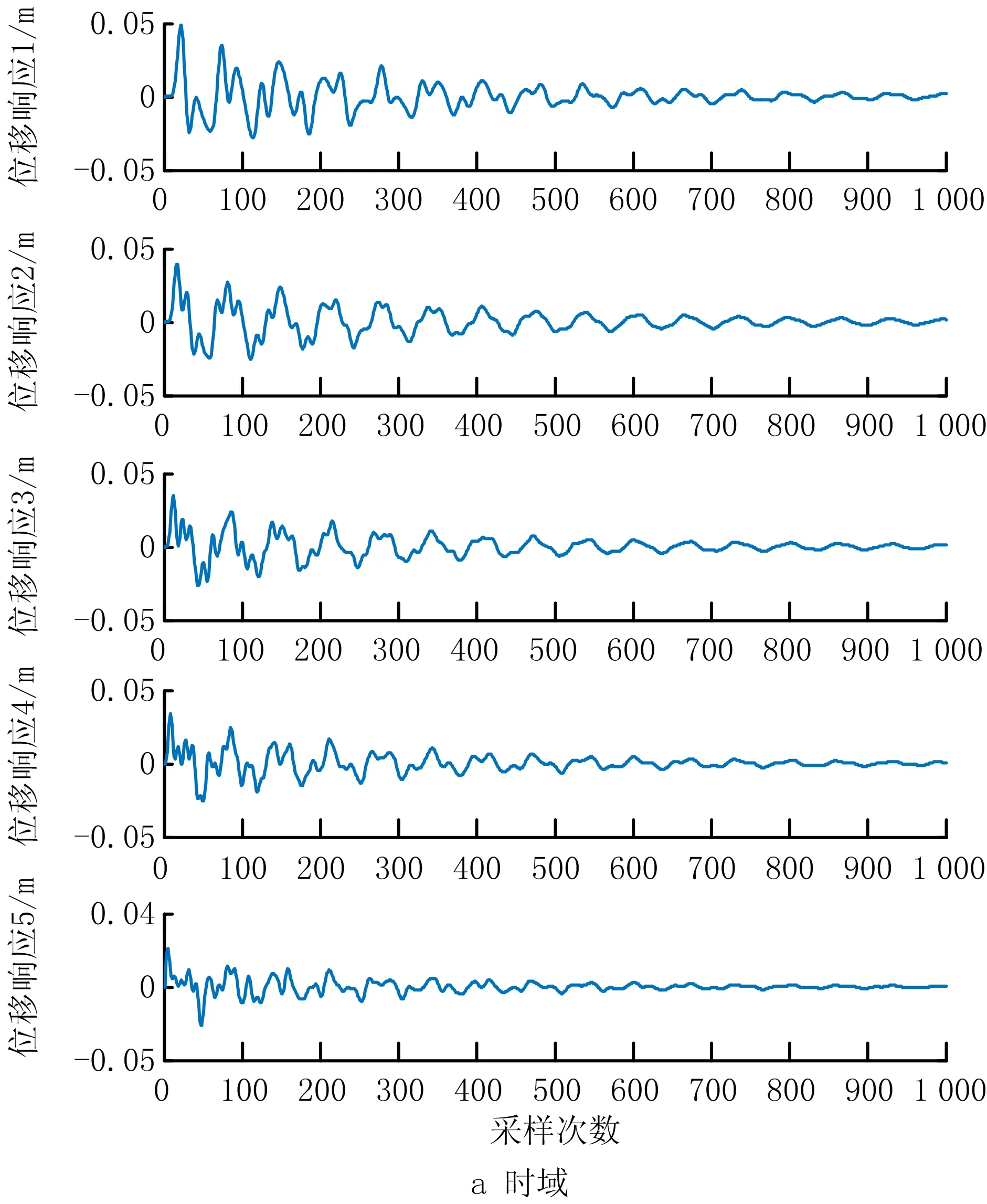
4.1 实验数据生成


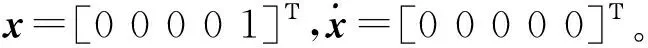

4.2 评价方法与指标

4.3 参数设置
4.4 实验结果










4.5 实验结果分析
5 结束语
