多目标离散灰狼优化算法求解作业车间节能调度问题

2021-09-11顾九春姜天华朱惠琦

计算机集成制造系统 2021年8期

顾九春，姜天华,2+，朱惠琦

(1.鲁东大学交通学院，山东烟台 264025；2.吉林大学符号计算与知识工程教育部重点实验室,吉林长春 130012)

0 引言

作业车间调度问题(Job shop Scheduling Problem, JSP)通过合理安排各机器上工件的加工顺序获得期望的生产性能，由于该问题具有很强的理论和应用背景，自提出以来，一直受到国内外研究学者的广泛关注，而且绝大多数JSP已被证明具有NP难特性。然而，传统JSP只考虑与时间、质量或成本等相关的经济指标，未关注与环境等相关的能耗指标，难以指导企业获得真正意义上的最大利润。

在当今能源危机日益严峻的形势下，绿色制造受到世界绝大多数国家的重视，而节能调度作为实现绿色制造的重要手段之一，已逐渐引起学者们的兴趣[1-2]。节能调度能够通过制定有效的调度方案，在提高生产效率的同时实现节能、降耗、降成本的目标，相比于传统JSP，节能调度问题的出现时间较晚，相关文献仍较少。LIU等[3]建立了一种以最小化总能耗量和工件总权重拖期时间为目标的数学模型，并提出一种非支配排序遗传算法进行求解；HE等[4]提出一种以最小化能耗和工件最大完工时间为目标的数学模型，并提出一种基于禁忌搜索的启发式算法；GONZLEZ等[5]针对JSP，以总权重拖期时间和总能耗为优化目标，提出基于Pareto的多目标进化算法、基于分解的多目标优化算法和约束优化方法进行求解；KEMMOE等[6]考虑具有能量阈值的JSP，提出一种基于局部搜索的贪婪随机自适应搜索算法进行求解；MAY等[7]以优化车间总能耗量和工件最大完工时间为目标，提出一种遗传算法求解多目标优化问题。由上述文献可知，在调度模型中引入与环境相关的能耗指标来同时优化经济指标和能耗指标，既能改善车间生产性能，又能达到节能降耗的目的。然而，目前作业车间节能调度的成熟程度远不及传统JSP，还需对该类问题进行进一步研究，以使研究成果更加贴近实际生产。例如，上述文献均假设车间内机器的加工速度是固定的，而在现实生产中各机器可根据实际情况以不同的工作速度运行，并对应不同的加工能耗和工件处理时间。一般情况下，机器加工速度越大，工件处理时间越短，加工能耗量越大；反之，机器加工速度越小，加工能耗量越小，工件处理时间越长，从而使降低车间能耗成为可能。JIANG等[8]针对具有多速度机器的作业车间，以最小化能耗成本和完工时间成本为目标，提出一种改进鲸鱼优化算法；SALIDO等[9]提出一种遗传算法用于求解具有多速度机器的作业车间节能调度问题(Energy-saving Job shop Scheduling Problem, EJSP)；JIANG等[10]针对含多速度机器的JSP，以优化车间能耗成本和完工时间成本为目标，提出一种离散鲸鱼优化算法。对于这类EJSP，需要考虑速度选择和工件排序两个子问题，通过合理选择机器的工作速度，并安排各机器上工件的加工顺序，达到节能降耗的目的。选择速度虽然增加了问题的复杂程度，但是使其更加贴近实际生产，具有一定实际应用价值。因此，本文以作业车间为对象，研究车间内机器包含多种工作速度的节能调度问题，提出一种同时优化工件最大完工时间和车间总能耗量的节能调度优化算法。

高效的优化算法有助于企业提高生产效率、降低能源消耗量，近年来智能优化算法已经成为节能调度问题主要的求解途径。灰狼优化算法(Grey Wolf Optimization algorithm, GWO)是根据狼群等级制度和捕食行为而提出的一种新型群智能优化算法[11]，该算法搜索原理简单、易于实现，而且具有较高的收敛精度和较快的求解速度，已成功用于求解多种优化问题[12-17]。然而，由于GWO最初用于解决连续优化问题，灰狼个体在连续域内进行位置更新，无法直接应用于车间调度问题，姜天华[18]提出一种连续个体位置与离散调度解间的转换方法，然而该方法需要在算法搜索过程中频繁转换，影响了算法的求解效率。为了克服这一缺点，JIANG等[19]提出一种离散GWO，通过个体与决策层个体的离散交叉操作体现GWO中决策层个体对其他个体更新的引导作用，使算法能够直接在离散调度域内运行，然而算法中的个体仍只根据决策层个体的信息进行更新，导致算法易出现早熟收敛。因此，本文采用一种双模式并行搜索机制，即算法每次迭代时先将整个狼群划分为两个子群，然后分别对子群内的个体执行搜寻操作和跟踪操作。在跟踪模式下，个体根据决策层个体进行更新，算法执行局部搜索；在搜寻模式下，个体根据记忆池机制进行更新，算法执行全局搜索。为了协调算法的全局搜索和局部搜索能力，在搜索过程中动态调整各子种群中的个体数量，使算法前期侧重于全局搜索，后期侧重于局部搜索。另外，针对本文多目标优化的特点，对GWO进行一系列设计和改进，提出一种多目标离散灰狼优化算法(Multi-Objective Discrete Grey Wolf Optimization algorithm, MODGWO)，并通过大量仿真对其有效性进行验证。

1 问题描述

(1)所有机器和工件在初始零时刻均为可用。

(2)每台机器同时只可加工一个工件。

(3)每个工件同时只能被一台机器加工。

(4)工件的加工过程不允许被中断。

(5)各工件间相互独立，同一工件不同工序间遵循一定的先后加工约束。

(6)不考虑机器故障和机器调整时间。

(7)在任一工件的加工过程中，机器的加工速度不允许被调整。

2 模型建立

2.1 车间能耗模型

本文车间总能耗可划分为加工能耗和空载能耗两部分，下面分别对各个能耗组成部分进行分析，建立车间能耗模型。

(1)加工能耗指机器加工工件所消耗的能量[20]，总加工能耗

(1)

式中xikl为0-1变量，若工件i在机器k以速度档l进行加工则xikl=1，否则xikl=0。

(2)空载能耗指机器在相邻工件的时间间隔内空载运行所消耗的能量，即前一个工件已加工完，而后一个工件还未到达时，机器空载运行所消耗的能量[20]。总空载能耗

(2)

式中：SEk为机器k单位时间内的平均空载能耗；MCk为机器k的完工时间；Wk为机器k的总负载，即机器k上所有工件加工时间之和。

根据上述分析，车间总能耗

(3)

2.2 作业车间节能调度模型

由前述可知，节能调度的目的是在提高生产效率的同时实现节能降耗。因此，本文以优化车间总能耗和工件最大完工时间为目标，建立如下数学模型：

minF1=EC1+EC2；

(4)

minF2=CTmax。

(5)

s.t.

(6)

i=1,2,…,n,k=1,2,…,m；

(7)

i,j=1,2,…,n,k=1,2,…,m；

(8)

(9)

MCk=max{Cik},i=1,2,…,n；

(10)

Cik≥0,i=1,2,…,n,k=1,2,…,m；

(11)

xikl∈{0,1},i=1,2,…,n,

k=1,2,…,m,l=1,2,…,dk；

(12)

yijk∈{0,1},i,j=1,2,…,n,k=1,2,…,m。

(13)

式(4)表示最小化车间总能耗；式(5)表示最小化工件最大完工时间；式(6)表示工件在机器上的加工速度一旦确定后不允许更改；式(7)表示同一工件内后道工序必须在前道工序完工后才能开工；式(8)表示任何机器在同一时刻只允许处理一个工件；式(9)表示机器的总工作负载；式(10)表示机器的完工时间；式(11)表示工序完工时间为非负；式(12)和式(13)表示0-1变量。

3 离散灰狼优化算法

3.1 基本灰狼优化算法

GWO是一种模仿狼群社会等级制度和捕食行为的群智能优化算法[11]。在算法每次迭代过程中，种群内的个体被划分为头狼α、下属狼β、普通狼δ和底层狼ω，前三者属于决策层个体，分别表示历史最优解、历史次优解和历史第三优解，ω对应其余个体。在算法迭代过程中，α，β，δ负责定位猎物的位置，并引导ω更新位置，通过完成靠近、包围和攻击等一系列行为来捕食猎物。限于篇幅，GWO的具体原理和步骤请参考文献[11]。

3.2 编码方法

本文采用基于速度—工序的编码方法，即每个调度解均包含长度相等的前后两段，分别对应速度选择方案和工序排序方案，如图1所示。其中O12表示工件1的第2道工序，其他工序依此类推。另外，前半段元素值表示各工序所在机器选择的加工速度，后半段元素值表示各工序所属工件的编号，相同元素值表示同一工件的不同工序，其出现的顺序表示工序加工的先后顺序。

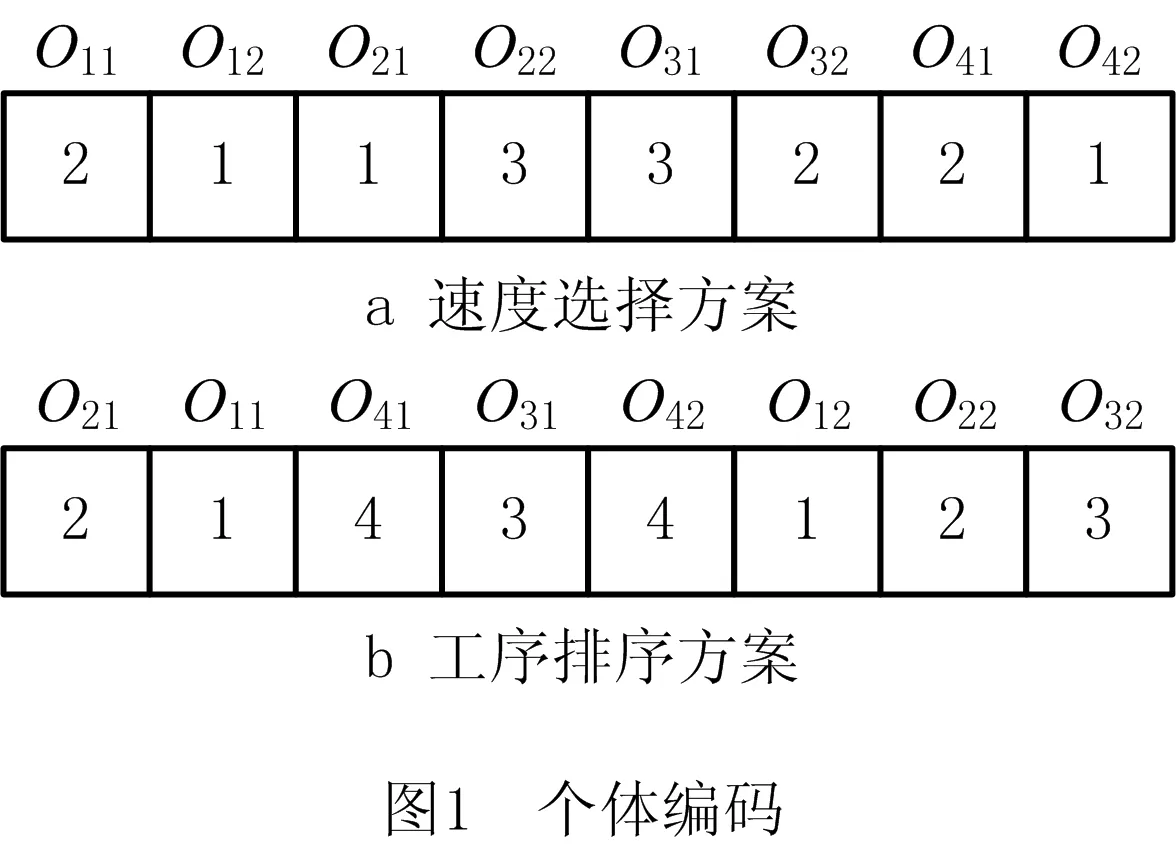
对于JSP，每个工件的加工路径已知，解码时从左到右扫描每个调度解后半段内的元素，并根据前半段元素的值确定每道工序所在机器的加工速度。处于后半段最左端的工序最先被调度，以尽可能早地在相应的机器上加工，并获得所有工序的开始时间和完工时间。其他工序以此类推，直到所有工序调度完为止。

3.3 种群初始化

对于一个群智能优化算法，初始解的优劣在很大程度上影响算法的计算性能。由于本文问题分为速度选择和工序排序两个子问题，种群初始化也分两阶段进行，对于每个个体，首先在前半段采用随机方式获得工序在相应机器上的速度选择方案，然后确定各工序的加工时间；后半段采用基于调度规则的方法，即以相同的概率选择剩余负荷最多(Most Work Remaining, MWR)优先[21]、剩余工序最多(Most Operation Remaining, MOR)优先[21]和随机规则(Random Rule, RR)获得工序排序方案。

3.4 Pareto排序

多目标优化问题无法直接根据适应度值比较个体优劣，需要通过Pareto排序将种群中的个体分为若干个非支配等级。首先找出当前种群中的非支配最优解，构成第一个非支配最优解层，并为其中个体的等级赋值为1级，然后将这些解从种群中去除，在余下个体中找出新的非支配解，给其中个体的等级赋值为2级，依此类推，直到所有个体均被分级。显然，等级数小的个体表现更优。

3.5 确定决策层个体

在基本GWO中，新个体由当前个体根据决策层个体α，β，δ的信息产生。然而，由于多目标优化问题无法直接通过比较适应度值的大小来确定决策层个体，本文采用基于非支配等级和拥挤距离的方法获得决策层个体，即根据种群中个体的非支配等级和拥挤距离对个体进行排序，排在最前面的3个个体有机会成为决策层个体。排序遵循的原则为：对于任意两个个体，等级低的个体排在前面；若两个个体等级相同，则比较二者的拥挤距离，拥挤距离大的个体排在前面。

首先根据上述排序原则从初始种群中选择排在前3位的个体，分别将其作为α，β，δ；其次，每代个体更新完成后，根据排序原则从当前种群中选出3个个体与当前决策层个体合并，从而获得一个子集；然后，对合并后子集内的个体进行排序，确定新的α，β，δ。

3.6 外部档案更新

为了存放搜索过程中的非支配解,建立一个外部档案，并基于Pareto支配关系对其进行更新，更新方法如下：对于一个新产生的解，若其被外部档案中的任一解支配，则拒绝其加入；若其支配外部档案中的部分解，则将其加入外部档案，并剔除受支配的解；若其与外部档案中的所有解均为非支配关系，则新解直接进入外部档案。

3.7 个体更新策略

在基本GWO中，个体只根据决策层个体的信息进行更新，可能导致在运行后期算法的种群多样性下降，出现早熟收敛。本文采用跟踪模式和搜寻模式的双模式并行搜索机制，分别对应局部搜索和全局搜索。每次迭代时，算法先将整个狼群划分为两个子群，再分别对子群内的个体执行搜寻操作和跟踪操作。为了协调算法的全局搜索和局部搜索能力，通过在搜索过程中动态调整各子种群中个体的数量，使算法前期侧重于全局搜索，后期侧重于局部搜索。

3.7.1 跟踪模式

与基本GWO相同，跟踪模式下的个体主要根据决策层个体的信息进行更新。然而，由于基本GWO不能直接用于离散调度问题，本文根据问题特点设计了一种基于交叉操作的个体更新方法，即个体按照一定概率与α，β，δ进行交叉操作，从而获得新的个体，如式(14)所示。

Xk(t+1)=

(14)

式中：Xk为灰狼k对应的调度解，Xα,Xβ,Xδ为α，β，δ对应的调度解；rand为一个0和1之间服从均匀分布的随机数；CR表示交叉操作，前半段采用两点交叉法，即在前半段任选两个位置，互换父代个体中被选位置间的元素，后半段采用文献[22]中的优先交叉操作(Precedence Operation Crossover，POX)。

需要注意的是，交叉操作后将获得两个子代个体，根据支配关系选择其中较优的个体作为新个体。若两个个体互不支配，则任选其中一个作为新个体。

3.7.2 搜寻模式

由跟踪模式可以看出，个体只根据决策层的个体信息进行更新。因此，本节引入搜寻模式，其主要思想是通过记忆池机制进行全局搜索，即预先设定记忆池的大小为MS，然后对当前个体进行扰动操作，生成MS个候选解并填满记忆池。通过评价记忆池中的所有个体，选择其中最优个体替代原来的个体，从而完成一个个体更新。不断重复该过程，直到搜寻模式下的所有个体均完成个体更新。在评价记忆池个体时，首先找出记忆池中的非支配解，然后将原个体与其进行比较，若原个体被记忆池中某些非支配个体所支配，则从这些个体中任选一个替代原来个体，否则保持原来个体不变。

根据本文问题的特点，随机执行以下一种或两种邻域结构进行个体扰动，邻域结构如下：

(1)速度选择随机选择一道工序，该工序对应机器的可选速度应多于一个，然后任选一个不同速度替代原来的值。

(2)工序排序随机选择两个属于不同工件的工序，然后互换被选工序的位置。

3.7.3 全局和局部搜索的平衡

为了平衡算法局部搜索和全局搜索的能力，动态调整两个子群中个体的数量，在算法运行前期侧重于全局搜索，随着迭代次数的增加，在算法后期侧重于局部搜索。

用MR表示搜寻模式下子种群内个体数量占整个种群的比率，其大小反映算法对全局和局部搜索的侧重程度。MR较大时，算法侧重于全局搜索；反之，算法侧重于局部搜索。MR的值可通过式(15)进行调节，其中MRmax和MRmin分别为1和0；t和tmax分别表示算法的当前迭代次数和最大迭代次数。

MR=MRmax-(MRmax-MRmin)×t/tmax。

(15)

3.8 算法步骤

基于前述，MODGWO的具体步骤如下：

步骤1设置算法参数，包括种群大小、记忆池大小和最大迭代次数。

步骤2采用第3.3节的种群初始化方法，获得初始调度解。

步骤3评价初始种群中的个体，确定决策层个体α，β，δ，并将非支配解加入外部档案。

步骤4判断是否达到算法终止条件，是则转步骤8，否则执行步骤5。

步骤5根据式(12)计算MR的值，并对狼群个体进行划分。

步骤6对于每个灰狼个体，若处于搜寻模式，则对其执行搜寻操作；否则，对其执行跟踪操作。

步骤7评价更新后的灰狼个体，更新决策层个体和外部档案，然后转步骤4。

步骤8算法结束，输出外部档案。

4 实验结果与分析

为了测试MODGWO的性能，采用FORTRAN语言进行编程，并在WinXP系统下内存为2 G的VMware Workstation上运行。

4.1 测试问题

基于所构造的算例，采用文献[24]中的比例指标和文献[25]中的距离指标评价算法性能：

(1)比例指标ζr指算法r所获非支配解集Sr提供的非支配解在整个参考集S*中所占的比例，

(16)

式中参考集S*是将所有算法的非支配解集合并而获得的非支配解的集合。可见，ζr值越大，算法得到的非支配解越多。

(2)距离指标IGDr指Sr中元素相对于参考集S*的距离，

(17)

4.2 参数分析

MODGWO主要包括种群大小PS、记忆池大小MS和最大迭代次数itermax3个参数。本节采用试验设计方法(Design of Experiment, DOE)对这3个参数进行设置。为此，建立一个三因素四水平L16(43)正交表，如表1和表2所示。

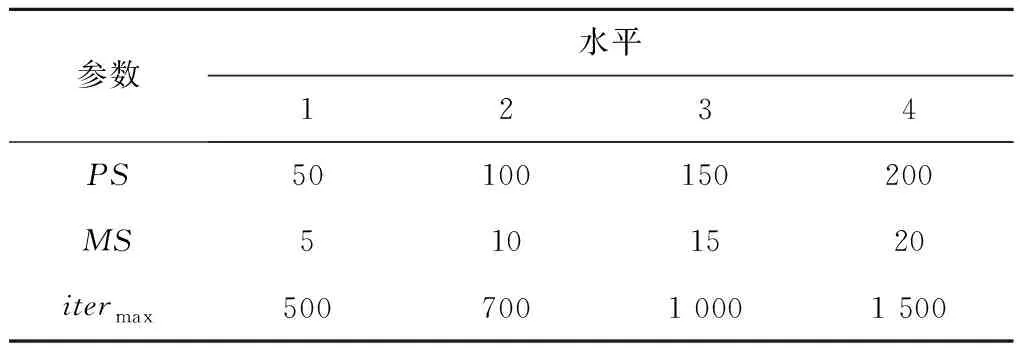
表1 参数水平

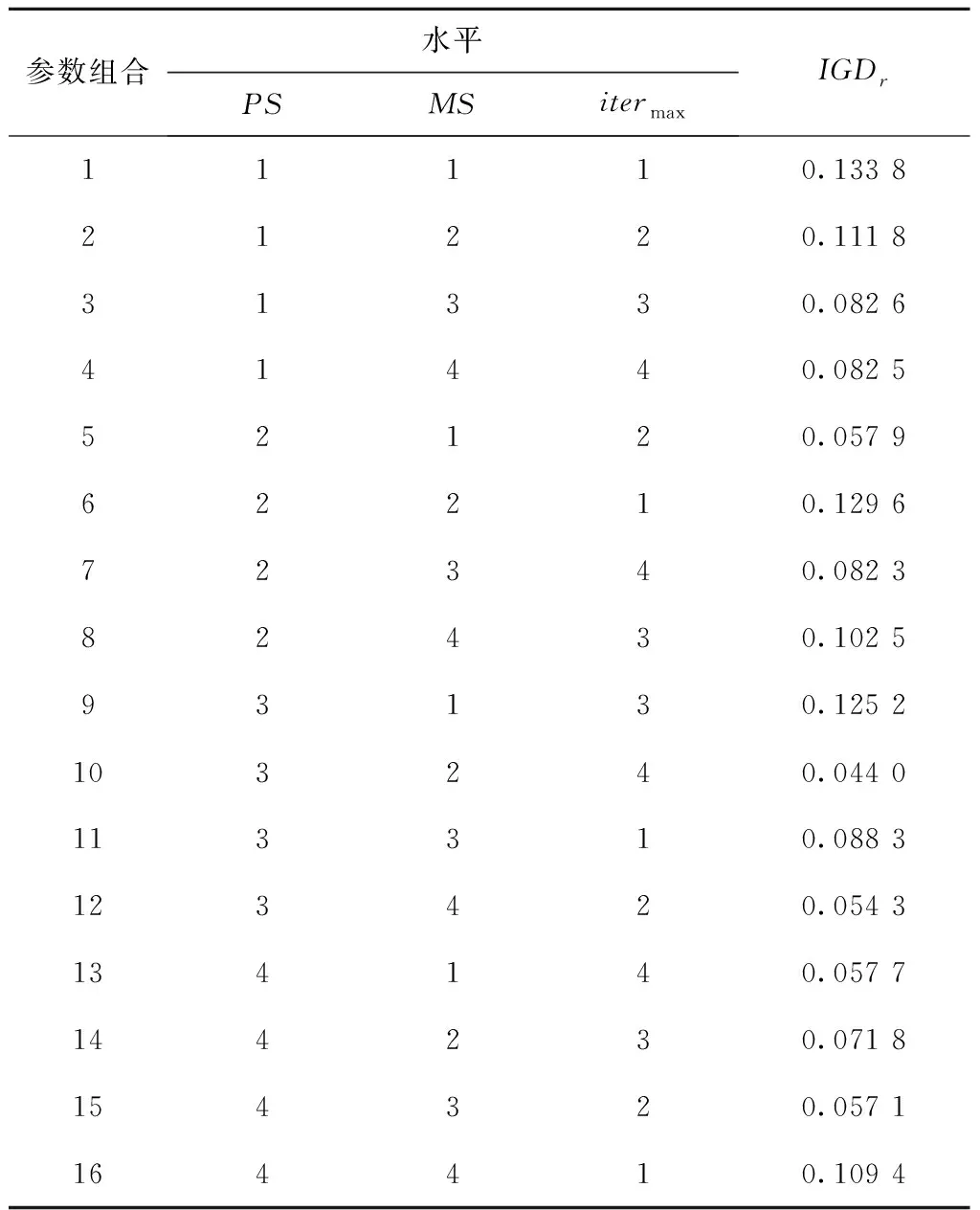
表2 正交表和IGDr值

针对算例LA25，将每种参数组合下的算法均独立运行10次，并以IGDr作为性能评价指标。根据表2中的数据计算各参数响应值，如表3所示，所绘制的算法参数对计算性能的影响曲线如图2所示。由表3可见，参数itermax的极差最大，表明该参数对算法性能影响最大，PS次之，MS影响最小。结合分析结果，将MODWWO参数设置为：种群大小PS=200，记忆池大小MS=15，最大迭代次数itermax=1 500。

表3 各参数的响应值

4.3 改进策略的有效性分析

本节主要分析种群初始化方法和双模式并行搜索方式两种改进策略的有效性，对比算法如下：

(1)A1算法表示MODGWO采用随机初始化方法获得初始解。

(2)A2算法表示MODGWO每次迭代时不划分种群，只采用单一的跟踪模式进行搜索。

(3)A3算法表示MODGWO。

针对算例LA01～LA40，各算法独立运行10次，采用IGDr，ζr，Time3个指标比较算法的性能，如表4所示。其中：Time为算法的平均运行时间(单位：s)；粗体表示算法获得的最佳值。由表4可见，对于IGDr和ζr指标，A3算法表现最好，其在37个算例中获得的IGDr值小于其他算法，在21个算例中获得的ζr值大于其他算法；对于Time指标，A1和A3算法的运行时间相差不大，均大于A2算法，主要原因是搜寻模式中的记忆池机制增加了算法的运行时间。

表4 改进策略有效性分析

续表4

4.4 与其他算法的对比分析

对于具有多速度机器的EJSP，文献[8-9]分别提出了鲸鱼优化算法和遗传算法，并通过仿真算例验证了算法的有效性。然而文献[8-9]研究的均为单目标优化问题，本文将这两种算法稍作修改，得到多目标改进鲸鱼优化算法(Multi-Objective Improved Whale Optimization Algorithm, MOIWOA)和多目标遗传算法(Multi-Objective Genetic Algorithm, MOGA)，并与本文所提算法进行了对比。

对于MOGA，首先基于本文的种群初始化方法获得初始调度解，并利用Pareto排序法确定个体等级；其次，选择算子采用二元锦标赛机制，从种群中随机选择两个个体，个体等级不同则优先选择等级较低的个体，个体等级相同则选择拥挤距离较小的个体；然后，采用文献[9]的方法进行个体交叉和变异操作。为了便于比较，对比算法的参数设置如下：对于MOIWOA，种群大小均为200，最大迭代次数为1 500；对于MOGA，种群大小均为200，最大迭代次数为1 500，交叉率为0.8，变异率为0.2。算法对比结果如表5所示。

表5 算法对比结果

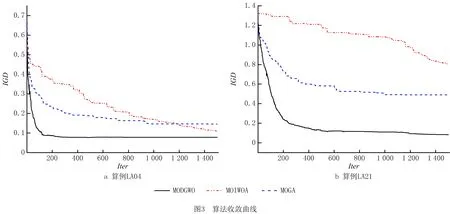
由表5可见，对于IGDr指标，MODGWO在39个算例中获得的IGDr值小于其他算法，而且22个算例中的IGDr值均为零；对于ζr指标，MODGWO在所有40个算例中获得的ζr值均大于其他算法，即能够产生参考集S*中的大多数元素，其中22个算例中整个参考集S*元素均由MODGWO产生；对于Time指标，MOGA运行时间最短，MODGWO的运行时间虽然大于其他算法，但是计算结果明显更优。为了进一步比较算法性能，图3给出3种算法在算例LA04和LA21下的收敛曲线，可见MODGWO的收敛情况明显优于其他两种算法。图4所示为算法在算例LA02和LA40下所获解的分布情况，可见总能耗量和工件最大完工时间之间存在冲突关系。根据图4中解的分布情况可以发现，MODGWO所获解优于其他两种算法。综上所述，MODGWO在求解本文多目标EJSP方面具有有效性。

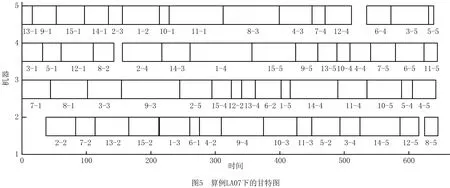
图5和图6所示分别为算例LA07和LA27下MODGWO所获得的甘特图，图中每个方框代表一道工序，方框下字符表示“工件—工序”，例如9-6表示工件9的第6道工序。

5 结束语

本文针对EJSP进行研究，建立以车间能耗总量和工件最大完工时间为优化指标的数学模型，并提出一种MODGWO。该算法采用速度—工序两段式编码方法表示调度解，基于调度规则实现种群初始化，然后引入双模式并行搜索方式，在搜索过程中动态调整全局和局部搜索的能力。为了使算法适用于多目标离散调度问题，提出一种基于个体非支配等级和拥挤距离的决策层个体选择策略，并设计了基于交叉操作的离散个体更新方法。最后，对传统JSP的40个基准算例进行改造，用于算法仿真测试，通过大量实验表明MODGWO在求解本文EJSP方面的有效性。