带有网络直销的双渠道制造商供应链中的定价和广告决策
2021-09-11李绩才刘燕飞楼婷渊李昌文周永务
李绩才,刘燕飞,楼婷渊+,李昌文,周永务
(1.浙江师范大学 行知学院,浙江 金华 321004;2.浙江师范大学 继续教育学院,浙江 金华 321004;3.淮北师范大学 经济与管理学院,安徽 淮北 235000;4.华南理工大学 工商管理学院,广东 广州 510641)
0 引言
近年来,开展广告促销是企业及其供应链提高商品消费需求最主要的商业策略之一。在我国,面对越来越激烈的市场竞争,各类型企业无论在常规品牌宣传还是节假日集中促销活动上,均纷纷加大投入。据电通安吉斯公司估算,2019年我国广告支出规模预计将增长7%,达到6 820亿元人民币,占全球广告支出的17%。根据作用的不同,广告进一步分为全国性广告和地方性广告,其中地方性广告由供应链下游零售商主导,在其零售终端市场通过开展宣传和促销刺激潜在消费者的真正购买行为[1]。目前,在各类零售商城、超市等零售环节,常采用海报宣传、人员促销、赠品等形式的地方性广告。
在地方性广告的实施过程中,供应链上游制造商经常与下游零售商合作分担地方促销广告支出,将其称为合作广吿[2]。制造商通过合作广告合同,诱使零售商增加其地方性促销广告投入,以刺激市场需求,增大商品销量,进而增加制造商利润。据统计,2015年在北美地区,制造商和零售商的合作广告开支约为360亿美元,占所有广告支出的12%[3]。
伴随着电子商务等互联网经济的持续发展,众多制造企业加快了转型步伐,纷纷启动电商渠道建设,进行线上线下双渠道经营。例如,作为国内家电领域的龙头制造企业格力电器,近年在继续完善线下传统零售渠道的同时,积极开拓在线销售渠道直接面向消费者,截止2018年底,格力在国内拥有26家区域性销售公司,线下销售网点有4万多家;同时通过自建格力网上商城并在天猫和京东平台开设官方旗舰店进行直销,仅2018年“双十一”期间,格力空调全网实现销售达12.59亿元,市场占比28.1%[4]。2019年“双十一”,格力电器线上渠道进一步发力,当天全网全品类销售额超41亿元,同比增长超200%。
目前,供应链合作广告问题的相关研究主要集中于采用单一渠道经营的供应链系统,这方面的早期研究一般均假定商品市场零售价为外生的情况下,对供应链处于不同市场博弈结构下的合作广告问题进行比较分析,这类研究如文献[5-7]。随后,学者们进一步考虑到商品零售价格对市场需求的影响,对同时进行合作广告与定价决策问题开展了研究,例如文献[8-10]。此外,文献[11-12]对单一渠道供应链中的合作广告决策议题研究进行了详细综述。
随着制造商越来越多地采用双渠道经营,有关双渠道制造商供应链系统中合作广告问题的研究开始受到关注,其中一类研究仅聚焦于供应链双方的合作广告决策,未涉及商品的定价决策问题,如文献[13-16]。与本文更相关的是另一类同时考虑供应链上下游的商品定价和广告投入决策的双渠道供应链合作广告问题。YAN等[17]针对一个双渠道制造商的供应链系统,给定制造商的商品批发价和对零售商广告投入的分担比例,分别分析了Bertrand和Stackelberg博弈结构下的零售商定价和合作广告策略,研究发现Stackelberg博弈结构对制造商更有利,零售商的收益不受两种博弈结构的影响;黄松等[18]在双渠道供应链系统中,由制造商投入广告且零售商愿意为其分担给定比例广告费用的情形下,分别分析了一体化供应链和基于Stackelberg博弈时分散式供应链的商品定价和合作广告决策问题;禹爱民等[19]针对制造商同时拥有传统零售渠道和网上直销渠道的双渠道供应链系统,其愿意承担给定比例的零售商广告投入以开展联合促销,在零售商面临给定商品批发价和随机市场需求的情况下,对供应链双方的价格竞争和协调问题进行研究,发现回购契约能给双方带来好处,但不能实现供应链协调;PEI等[20]假定零售商的地方性广告支出完全由制造商承担,当制造商选择开设线上直销渠道与其零售商竞争时,研究发现所新增的在线渠道对制造商广告支持政策影响显著,而且影响的方式与程度因产品的在线销售适应度而异;XIE等[21]针对一个双渠道制造商的闭环供应链系统,制造商分担给定比例的零售商广告投入,并可获得零售商分享的给定比例传统渠道销售收入,零售商可分享到给定比例的制造商回收再造节省成本,对比分析了集中决策和制造商主导的分散决策情形的线上/线下商品价格和广告投入策略,发现无论是集中决策还是分散决策,合理地设置回收再造节省成本的分担比例对协调供应链至关重要。
然而,目前有关双渠道制造商供应链中的商品定价和合作广告问题研究,部分文献假设双渠道制造商提供给零售商的商品批发价是外生给定的常量,如文献[17,19];另外,几乎所有文献均假定制造商开展合作广告计划时给予零售商地方性广告支出的分担比例也是外生给定的,而非作为供应链双方博弈的决策变量[17-21]。这些出于简化分析目的的假设与现实中绝大多数供应链系统的合作广告运作实情并不相符,实际上制造商一般会根据不同商品的特点(如商品的需求弹性系数、生产成本、在线销售兼容度等),从最优化自身运营绩效的目的出发,决策向线下零售商提供不同的商品批发价和合作广告参与比例,这在一些制造商发布的合作广告协议中可以看到[22-23]。同时,所有单一传统渠道供应链中商品定价与合作广告问题的研究,也将商品的批发价格和合作广告分担比例作为制造商的决策变量,而不是外生给定的[11-12]。
鉴于此,本文以开展网络直销业务的双渠道制造商供应链系统为研究对象,考虑双渠道中商品定价和零售商地方性广告对渠道需求的联合影响,为使所得到的双渠道供应链的定价和广告策略更加符合实际,制造商的商品批发价、参与零售商开展合作广告时的广告分担比例均将由其以最优化自身收益为目的进行决策,并从供应链双方均无广告投入、完全由零售商自身承担其地方性广告投入和供应链双方开展合作广告3种不同情形分别构建博弈决策模型,详细分析和比较讨论不同情形下的双渠道商品定价和广告投入策略,以期对开展大量双渠道经营的供应链企业进行合理地商品定价和广告决策提供参考。
1 问题描述及相关假设
考虑一个上游制造商同时通过线下和线上渠道销售一种商品给终端消费者;线下传统渠道采取和一个零售商合作的模式进行销售,线上渠道采用在线直销模式。零售商从制造商处按照批发价w采购该商品,以线下零售价pr售卖给消费者;制造商的在线直销零售单价为pd。两个渠道的商品需求量必然是关于自身渠道的零售价格递减,关于另一竞争渠道的零售价格递增。参照文献[24-25],假设两个渠道面临的需求函数为线性形式,表示为:
(1)
(2)
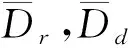
为简化运算过程并确保不影响所得结论,假定β1=β2=β,γ1=γ2=γ,并进行归一化处理,使β+γ=1,0<γ<1,采用类似假设的如文献[24,26-27]。因此,零售商传统渠道和制造商在线直销渠道的商品需求函数可简化为:
(3)
(4)
以制造商双渠道销售模式中仅涉及商品定价的基本问题为基础,进一步融入供应链双方的广告投入决策问题。为了更好地开拓市场和刺激消费者需求,零售商将开展地方性的广告宣传或促销活动,这必然会刺激零售商自身传统渠道的产品需求量增长,同时由于这些广告宣传促进了品牌传播,也会对制造商在线直销渠道的商品销售产生正向溢出效应。假设零售商的广告宣传努力程度为A,则零售商开展广告宣传时零售商传统渠道和制造商在线直销渠道的需求函数分别为:
Dr=(1-θ)α-pr+γpd+kA;
Dd=θα-pd+γpr+δkA。
式中:Dr,Dd分别为零售商开展广告活动时其自身传统渠道和制造商在线直销渠道的商品需求量;k(0≤k≤1)为广告活动对零售商传统渠道商品需求量的直接影响系数,k值越大,广告活动的商品促销效果越好;δ(0≤δ≤1)为零售商广告活动对制造商在线直销渠道商品需求量的间接溢出效应系数,δ值越大,溢出效果越好。
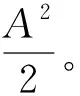
为方便表述和分析,制造商的单位生产成本将被简化为0。另外,假定1/2≤θ<1,即商品应具备一定的在线销售兼容度,从而保证pd≥w,以避免出现零售商为追求更低的采购价选择从制造商的在线直销渠道采购这一不合理的情形。
因此,在供应链双方均不进行广告投入时,零售商和制造商获得的利润分别为:
πr=[(1-θ)α-pr+γpd](pr-w);
(5)
πm=(θα-pd+γpr)pd+
[(1-θ)α-pr+γpd]w。
(6)
而当双方开展合作广告营销投入时,零售商和制造商所获得的利润分别为:
πr=[(1-θ)α-pr+γpd+kA]
(7)
πm=(θα-pd+γpr+δkA)pd+
(8)
2 产品定价与广告决策分析
针对上述由一个双渠道制造商和一个零售商组成的两级供应链系统,本文将分别构建供应链双方均无广告投入、完全由零售商自身承担其地方性广告投入、供应链双方开展合作广告共同分担地方性广告投入3种不同情形下的博弈模型。双渠道制造商和零售商之间的决策问题属于Stackelberg博弈,其中制造商为领导者,零售商为追随者,博弈双方通过确定各自的决策变量实现自身利润的最大化。下文分别用顶横“-”、上标“NC”和“C”分别表示这3种情形下的最优决策解。
2.1 供应链双方均无广告投入时的商品定价决策
针对制造商和零售商均不进行广告宣传投入的供应链系统,作为博弈决策的领导者,制造商先发布商品的批发价w和在线直销价pd;作为跟随者,零售商在此基础上再决策线下零售定价pr。下面借助逆向归纳法分析双方的博弈决策结果。

(9)
将式(9)代入制造商的利润函数式(6)进行简化计算,得
(10)

(11)
(12)
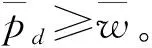
将式(11)和式(12)代入式(9),得到零售商的最优零售定价
(13)
进一步将式(11)~式(13)分别代入式(5)和式(6),得到供应链参与双方均不投入广告宣传时制造商和零售商的利润分别为:
(14)
(15)
2.2 制造商不分担零售商广告投入时的商品定价与广告决策(t≡0)
当零售商在其线下销售渠道中开展商品的广告宣传活动并承担所有广告投入,而制造商不分担零售商广告投入时(即t≡0),制造商作为博弈的领导者先决定商品的批发价w和线上直销单价pd,零售商再进一步确定其最优的广告努力程度A和市场零售定价pr。此时,零售商和制造商获得的利润分别为:
(16)
πm=[θα-pd+γpr+δkA]pd+
[(1-θ)α-pr+γpd+kA]w;
(17)
同样采用逆向归纳法求解双方的博弈决策均衡解。首先,在博弈的第二阶段,零售商作为博弈的追随者根据制造商给定的商品批发价格和线上直销单价,以实现其利润最大化为决策准则,就选择最优的广告宣传投入和市场零售定价做出反应。对式(16)分别求πr关于A与pr的二阶导数,可以较容易地验证πr的海森矩阵是严格负定的,即πr是关于A与pr的联合凹函数。令πr关于A与pr的一阶偏导数等于0并进行求解,可得零售商关于A和pr的最优反应函数分别为:
(18)
(19)
将式(18)和式(19)代入式(17),则制造商的利润表示为
[(γ+δk2)pd+w]+(θα-pd+γw)pd。
(20)
由此,在博弈的第一阶段,制造商关于其商品线上直销单价pd和批发价w的决策目标是使式(20)最大。对式(20)分别计算πd(pd,w)关于pd与w的二阶导数,可知当4(1-γ2)(2-k2)-(γ+δ)2k4>0时,πd(pd,w)是关于pd与w的联合凹函数,而且存在唯一的最优解使其取得最大值;否则,πd(pd,w)不存在极值点。于是,令πd(pd,w)关于pd与w的一阶偏导数分别等于0,联立求解可得制造商最优的批发定价和线上直销单价分别为:
wNC=α{2(1-θ+θγ)(2-k2)-(γ+δ)
[(2θ+γ-θγ)-(θ+θδ-δ)k2]k2}/
[4(1-γ2)(2-k2)-(γ+δ)2k4];
(21)
(22)

ANC=αk
(23)
(24)
最后,将式(21)~式(24)代入式(16)和式(17),得到制造商不分担零售商广告投入情形下的制造商和零售商利润分别为:
(1-θ+θγ)-(γ+θ-θγ)(θ+θδ-δ)k2]/
[4(1-γ2)(2-k2)-(γ+δ)2k4];
(25)
(26)
值得注意的是,从供应链运作的合理性出发,只有当式(21)给出的制造商批发价wNC>0时制造商才会有给零售商提供货源的积极性。因此,为了使制造商不分担零售商广告投入情形下的供应链博弈双方存在合理的均衡解,给出定理1。
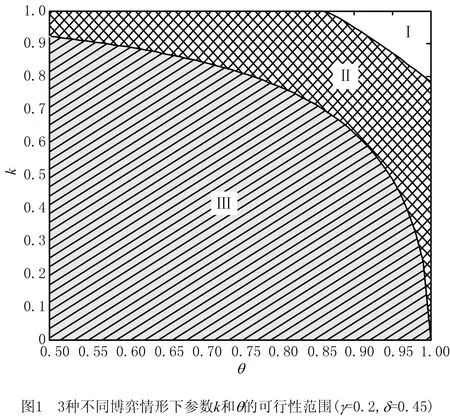
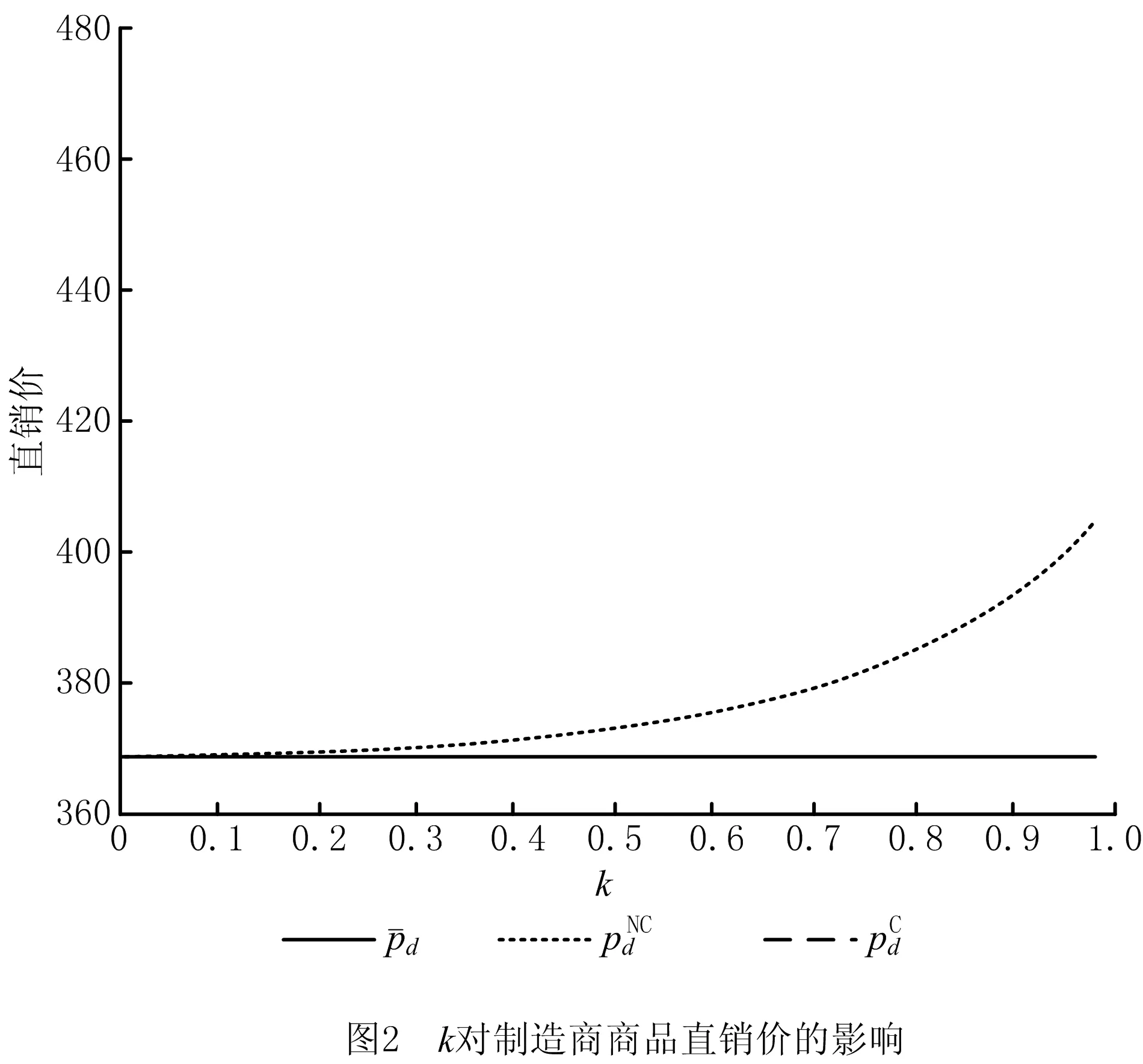
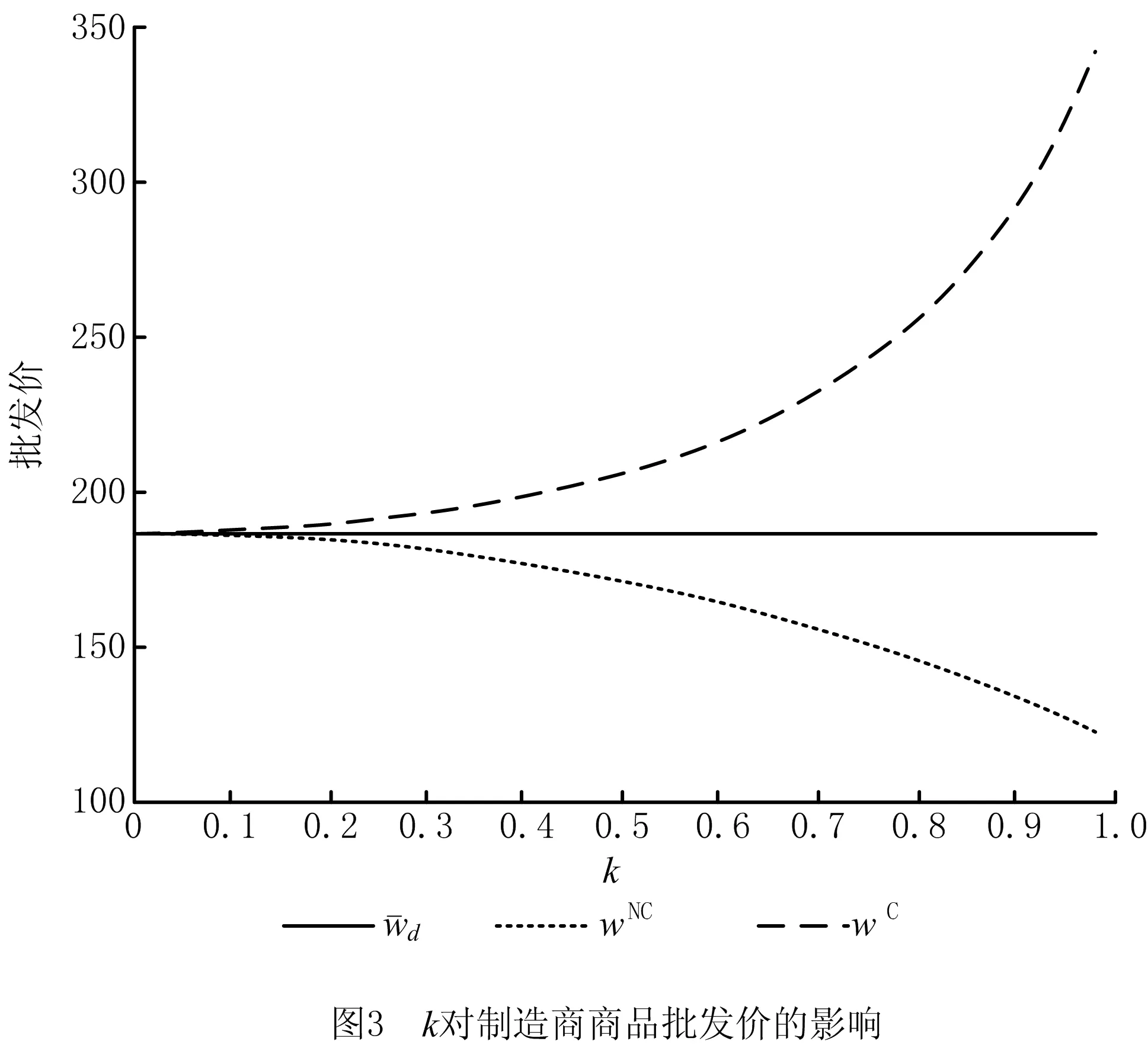
定理1对于给定的1/2≤θ<1,0<γ<1,0≤δ≤1,仅当零售商地方性广告宣传的直接影响系数k(0 4(1-γ2)(2-k2)-(γ+δ)2k4≥0, (27) 2(1-θ+θγ)(2-k2)-(γ+δ) [(2θ+γ-θγ)-(θ+θδ-δ)k2]k2>0 (28) 时,制造商不分担零售商广告投入情形下供应链双方的商品定价与广告投入决策才存在由式(21)~式(24)给出的合理博弈均衡解。 限于篇幅,文中定理及相关推论的证明从略。 当制造商愿意与零售商开展合作广告计划时,为了分别最优化自身利润,制造商首先发布其商品的在线直销售价pd、批发价w和参与零售商广告投入的分担比例t,零售商在此基础上再决策其零售定价pr和广告宣传努力程度A。类似于前两节的分析,可得双方的博弈决策结果。 pr(w,pd,t)= (29) (30) 在此基础上,将式(29)和式(30)代入式(8),并进行最优化分析,可以发现只有当(1-γ2)(16-9k2)-8(γ+δ)2k2>0时,制造商的利润函数才会在(pd,w,t)的合理取值范围内存在极大值点。此时,制造商关于pd,w,t,以及零售商关于A和pr的最优决策解分别为: (31) (32) tC=1- (33) (34) (35) 其中:ε=2(θ+θδ-δ)+(γ+θ-θγ),η=2(θ+θδ-δ)-3(γ+θ-θγ)。 将上述供应链双方的各项最优决策解代入式(7)和式(8),得供应链双方开展相互合作广告时制造商和零售商的利润分别为: (36) (37) 定理2对于给定的1/2≤θ<1,0<γ<1,0≤δ≤1,只有当零售商的地方性广告宣传直接影响系数k满足 (38) 时,制造商分担地方性广告支出情景下供应链双方的商品定价和广告投入决策才会存在由式(31)~式(35)给出的合理博弈均衡解。 另外,通过较为繁琐的推导得出,当满足式(38)时,定理1中制造商不分担零售商广告投入情景下供应链合理博弈均衡存在的必要条件式(27)和式(28)也成立。因此,上述3种情形供应链中博弈均衡存在的可行性条件越来越严格,对应参数的可行性范围会愈来愈小。为更加形象地说明这一结论,图1给出了限定γ=0.2,δ=0.45时,不同博弈情形下参数k取值的可行性范围随参数θ变化的情况。当供应链双方均无广告投入时(即情形1),参数k与θ的可行性范围为图1所示的整个区间,即区域Ⅰ,Ⅱ,Ⅲ;当零售商进行广告宣传投入而制造商不愿意分担时(即情形2),参数k和θ的可行性范围为区域Ⅱ,Ⅲ;当制造商合作分担零售商的广告宣传投入时(即情形3),参数k和θ的可行性范围仅为区域Ⅲ。 第2章已经根据有无合作广告投入策略构建了3种情形的供应链决策模型,并得到了不同模型中各参与方的博弈均衡决策解及其对应的利润,本章将对上述理论建模的博弈均衡结果进行分析与比较,以更好地解释现实中一些商业现象背后的内在原因,并挖掘富有运营意义和参考价值的管理启示。 下面结合不同供应链决策情形下的博弈均衡结果,针对相关参数展开灵敏度分析,讨论各参数变化对参与方博弈决策解及其利润的影响。 当零售商对其销售的商品开展广告宣传时,由式(23)和式(34)得到其进行广告宣传的努力程度与各相关参数间的单调关系。 推论1当零售商对商品开展广告宣传时,无论上游采取线上线下双渠道经营的制造商是否愿意分担广告宣传支出,其广告宣传的努力程度(ANC或AC)与该商品线上销售的兼容度系数θ负相关,与零售商广告的直接影响系数k、间接溢出系数δ和双渠道之间可替代性系数γ均正相关。 推论1表明,当零售商对其所销售的商品进行地方性广告宣传时,若该商品对制造商的在线渠道销售具有更高的兼容性,则不论制造商是否愿意分担零售商的广告支出,零售商开展广告活动的积极性都会更低。这背后的原因是,对于在线渠道销售更为兼容的商品,会有更大比例的消费者选择在线渠道购买;同时,由于零售商的地方性广告活动存在溢出效应,在一定程度上也会对其制造商及线上渠道起到品牌宣传和扩大知晓面的作用。因此,出于自保,零售商会更加不乐于进行广告宣传。其次,不论零售商地方性广告能够促进其自身线下渠道销售,还是促进制造商在线销售的溢出效应,都会促使零售商加大开展广告活动的努力程度。推论1还提示,制造商线上线下双渠道之间的相互可替代性程度越高,零售商越将增加其进行广告活动的努力程度,从而增加两个渠道商品的需求量,减弱渠道间的竞争压力。 推论2进一步给出了双渠道制造商与其线下零售商进行合作广告营销时,制造商参与零售商广告支出的最优分担比例关于各相关参数的单调关系。 推论2当零售商对商品开展广告宣传,且上游双渠道制造商愿意为其分担广告宣传支出时,制造商参与零售商广告支出的最优分担比例tC将分别与商品线上销售的兼容度系数θ、线上线下双渠道间可替代性系数γ、零售商广告的间接溢出系数δ正相关,与零售商广告的直接影响系数k负相关。 从推论2可知,双渠道制造商愿意为其零售商的地方性广告活动分担部分支出,当商品更适合在线销售或者双渠道间的可替代性程度更高时,制造商会加大对合作广告的参与度,分担零售商广告投入的比例更高。因为无论是商品更适合在线销售,还是双渠道的可替代性更高,都意味着两个渠道间的竞争加剧,此时制造商应承担零售商更高的广告投入分担比例,鼓励零售商加大其广告活动的努力程度,通过刺激商品市场需求来缓解渠道间的竞争压力。推论2还表明,零售商的广告活动对其线下渠道销售的直接促进效果越强、对制造商线上渠道的间接溢出作用越弱,制造商进行合作广告的参与度越低。 针对2.1节双渠道制造商供应链双方都不开展广告活动的情形,对供应链双方及整体的利润关于相关参数进行灵敏度分析,可得推论3。 推论3表明,当双渠道制造商的供应链双方都不进行广告宣传投入时,制造商及供应链整体利润都会随双渠道间的相互可替代性程度和商品对线上销售兼容性程度的上升而增加,意味着制造商和供应链整体可以从线上线下双渠道之间竞争强度的不断加剧中获利。同时,零售商利润会随商品线上销售兼容性程度的上升而降低,却不受双渠道之间可替代性程度的影响。这是因为,当供应链双方都没有广告投入时,商品越适合在线销售,对零售商的线下渠道销售越不利;当双方达到博弈均衡时,零售商线下渠道的商品销售量和单位商品的边际收益均不受两个渠道间可替代性程度的影响。 当零售商开展地方性广告活动时,针对制造商是否分担零售商广告投入两种不同的情形,就供应链双方的利润关于各相关参数进行单调性分析,可得推论4。 从推论4可知,当零售商开展地方性广告活动时,制造商双渠道间的相互可替代性程度越高、零售商广告活动对促进两渠道销售的效果越好,制造商的获利性越好。因为制造商双渠道间的相互可替代程度越高,或者广告活动的促销效果越好,越能促使零售商提高广告努力程度,不仅有利于零售商自身线下渠道的商品销售,还能提升制造商线上直销渠道的销售量。但是,参数γ,k,δ对零售商利润的影响将与双渠道制造商是否参与其合作广告有关。若制造商不参与开展合作广告,则双渠道间的相互可替代性程度越高,广告活动对促进销售的效果越好,越有助于提升零售商利润;若制造商参与合作广告,则其对零售商利润的影响比较复杂且不固定,笔者将在后文结合数值算例进一步展开讨论。 当零售商开展地方性广告活动时,商品线上销售兼容度越高,对零售商越不利。此时,零售商不但受制造商线上渠道更大竞食作用的影响,而且从推论1可知,零售商愿意付出的广告努力程度也会更低,从而阻碍其进一步扩大线下销售。 本节对第2章3种不同情形下双渠道供应链博弈均衡结果进行比较分析。为了保证相互间的可比性,并使相关结论对企业的实际运营决策更具借鉴意义,限定各参数之间满足条件式(38),以保证各供应链博弈情形均存在合理的博弈均衡。 推论5表明,当双渠道制造商愿意参与合作广告时,零售商将会在地方性广告活动上付出更大的努力程度,至少是制造商不提供合作分担时零售商广告努力程度的1.5倍。而且,随着商品在线销售的兼容性、制造商双渠道间的替代性程度或零售商广告对促进制造商在线直销渠道销售的溢出效应的增强,零售商广告努力程度在这两种不同情形下的差距将会不断变大。这是因为面临上述各种变化时,参与合作广告的双渠道制造商会为其零售商的广告投入分担更大的比例,使零售商在广告活动上更加卖力,与双方不进行合作广告情形相比,零售商广告努力程度的差距不断加大。 本章采用数值分析方法更加直观地展示前面的理论分析结果,试图揭示更多理论分析过程中尚未发现的规律和启示。 首先,在参数k和θ的可行区间范围内分析广告活动的直接促销效果和商品在线销售的兼容性对零售商广告努力程度的影响。设α=1 000,γ=0.1,δ=0.25,当k和θ在满足式(38)的可行范围内变化时,零售商广告努力程度的变化情况如表1所示。 表1 k和θ对零售商广告努力程度的影响 从表1可见,当零售商进行地方性广告活动时,无论其双渠道制造商是否愿意参与合作广告,零售商广告努力程度均会随商品线上销售兼容度的提升而不断降低,随广告对促进线下渠道销售效果的改善而不断增强。同时,制造商参与合作广告情形下的零售商广告努力程度至少是制造商不参与合作广告情形下的1.5倍,并且这种差距会随商品对线上销售兼容程度的提升而持续增大。这些结论与推论1和推论5的理论分析结果一致。从表1还发现,上述AC与ANC之间的比值关于参数k的单调性关系并不固定,当商品对线上销售的兼容性较差时,AC/ANC会关于参数k先减后增;当商品对线上销售的兼容性达到一定程度时,AC/ANC随k值的增大而不断减小。 在模型相关参数的可行区间范围内仿真对比分析3种不同情形下的商品定价决策。图2和图3所示分别为其他参数不变时(α=1 000,γ=0.1,δ=0.25,θ=0.7,特别是其他不同组的数值仿真结论均一致),3种不同情形下制造商商品直销价和批发价与零售商广告活动直接促销效果间的关系。 当给定参数α=1 000,γ=0.1,δ=0.25,商品具有不同在线销售兼容度时零售商线下渠道零售价与广告促销效果之间的关系如图4所示。当供应链双方开展合作广告时,零售商线下渠道的零售价总是比其他两种情形高,而且随广告活动促销效果的提升而提高,可见双方合作广告计划的实施会推高双方的各种商品定价。然而,零售商进行广告活动而制造商并不参与合作广告时,广告促销效果与线下渠道零售价之间的关系将同时受商品在线销售兼容度的影响。当商品在线销售兼容度低于一定阈值时,广告活动促销效果的不断改善将同步提高传统渠道零售价;而当商品的在线销售兼容度达到一定高度时,随着广告活动促销效果的改善,传统渠道零售价呈先降低后提高,甚至持续降低的趋势。可见,在零售商进行广告活动而双渠道制造商不分担广告投入的情况下,虽然零售商承担了全部广告支出,但是对于在线销售兼容度高的商品,为了抵挡制造商线上渠道的竞争,零售商甚至会通过降低商品零售价来吸引消费者。 在相关参数的可行区间范围内针对3种不同决策情形,分析零售商的广告活动对供应链双方和整体利润的影响。给定α=1 000,γ=0.1,δ=0.25,θ=0.7时,图5~图7所示分别为零售商广告活动的直接促销效果系数k取值变化对供应链双方及整体利润的影响。需要指出的是,其他不同组的数值仿真结论均一致,限于篇幅,不再赘述。 由图6可见,相对于零售商不进行地方性广告活动的情形,在零售商开展广告活动且其双渠道制造商不分担任何广告投入时,零售商能够获得更高的盈利水平;而且广告活动的促销效果越明显,零售商的盈利提升得越高。因此,当制造商采取双渠道经营时,其零售商可以通过开展地方性广告活动来挖掘市场潜力和提升双渠道的商品需求,以抵挡来自制造商线上直销渠道的竞争,即使零售商承担了所有广告投入,由于零售商和制造商的利润都能得到大幅提升,零售商也很乐意为之。 然而由图6可知,对零售商而言,当其开展地方性广告活动且双渠道制造商愿意分担广告投入时,零售商不能从双渠道制造商的合作广告策略中获利,其盈利始终低于双渠道制造商不分担广告投入时,甚至当广告促销效果达到一定水平时,供应链双方合作开展地方性广告投入情形下的零售商利润还会低于其不开展任何广告活动的利润。因此,虽然双渠道制造商与零售商开展合作广告时供应链整体利润能够大幅提升,但是零售商更希望双渠道制造商不参与合作广告而完全由自己承担全部广告投入。双渠道制造商为了鼓励零售商自愿接受其所提供的合作广告计划,除了按一定比例分担零售商地方性广告投入外,还应将双方开展合作广告营销时供应链系统所增加的收益进行合理分割,让双方共享系统整体的利润增值而达到共赢。 在当前我国互联网经济蓬勃发展的背景下,许多制造企业会同时利用线上直销渠道和线下传统渠道进行销售,因此双渠道供应链系统在现实中普遍存在。商品定价和广告投入决策是双渠道供应链管理中的重要问题,例如文献[17-21]针对不同商业情景下双渠道制造商供应链系统中的商品定价和广告投入决策问题进行了探索。然而通过文献梳理后发现,目前相关研究大多出于简化需要而假设制造商的商品批发价或者开展合作广告计划时对地方性广告支出的分担比例为预先给定的常数值,但是这些假设与现实生活中双渠道制造商的供应链运作的实际情况并不相符,现实中更多时候由制造商与其零售商在线上线下渠道商品定价和广告投入的博弈过程中决策。 有别于以往文献,本文的主要贡献如下: (1)为了弥补现有研究在假设条件简化处理上的不足,针对双渠道制造商供应链系统中的商品定价和合作广告问题,将制造商的商品批发价、参与合作广告的分担比例作为与零售商进行博弈的决策变量,使得所构建的理论模型更加符合企业运作的实际情况,所得结论和启示能够更好地指导双渠道供应链运营。 (2)创新性地同时融入线上线下双渠道间竞争、商品定价和合作广告等议题,分别从供应链双方均无广告投入、完全由零售商自身承担其地方性广告投入、供应链双方开展合作广告3种不同情形构建供应链博弈决策模型,对不同情形下的双渠道商品定价、广告投入策略,以及供应链各方和整体的利润进行了详细分析和比较讨论。 (3)通过理论和数值分析,考察了商品的在线销售兼容度、双渠道间的竞争强度等因素对不同博弈情形中的商品批发价,以及双渠道零售定价、广告投入和合作广告参与度的影响,这些正是在预先给定制造商的商品批发价和参与合作广告的分担比例时无法得到的管理启示。 本文研究得到的主要结论简述如下: (1)商品在线销售兼容度越高,零售商愿意付出的广告努力程度越低,而双渠道制造商对合作广告的参与度将会越高;双渠道间的相互可代替度越强,渠道竞争越激烈,越会促使零售商和制造商分别增加其广告宣传的努力程度和对合作广告的参与度。 (2)制造商的合作广告计划会增强零售商的广告努力程度,且与双方非合作情形下的差距会随商品在线销售兼容度的提高而不断增大;制造商合作广告计划使供应链在广告宣传上增加的投入将进一步推高供应链各方对商品的各种定价(包括商品批发价和线上线下零售价)。 (3)当零售商开展地方性广告活动时,如果希望双渠道制造商与其(不与其)合作分担广告支出,则需要支付比不进行广告活动更高(低)的商品批发价。 (4)当零售商不开展地方性广告活动时,商品线上销售的兼容度越高,对制造商利润提升越有利,对零售商获利越不利;但在零售商进行地方性广告活动的情况下,无论双渠道制造商是否愿意分担合作广告,只有当商品线上销售的兼容度达到较高水平时才有助于提升制造商利润,否则商品越适合在线销售,双渠道制造商的利润越低。 (5)零售商的地方性广告活动能够提升双渠道制造商和供应链整体的利润水平,制造商参与合作广告则能够进一步提高制造商和供应链整体的利润;然而,零售商在从事广告宣传活动时不希望双渠道制造商采用合作广告计划,如果希望双渠道制造商合作广告计划顺利实施,则应让供应链双方共同分享系统整体利润的增加值。 研究结论可为正在开展网络直销业务的双渠道制造商供应链系统制定商品定价和合作广告运营战略提供参考。后续研究可从新零售环境下采用O2O(online to offline)运作模式、面对策略型消费者的供应链商品定价与合作广告问题展开。2.3 供应链双方开展合作广告时的商品定价与广告决策
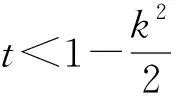

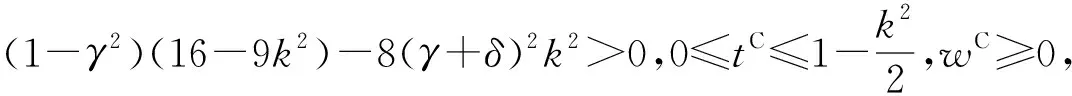
3 灵敏度分析与比较讨论
3.1 相关参数的灵敏度分析

3.2 不同情形下博弈均衡结果的比较分析

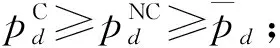
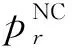
4 数值仿真分析
4.1 参数k和θ对零售商广告努力程度的影响

4.2 商品定价比较分析
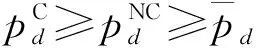

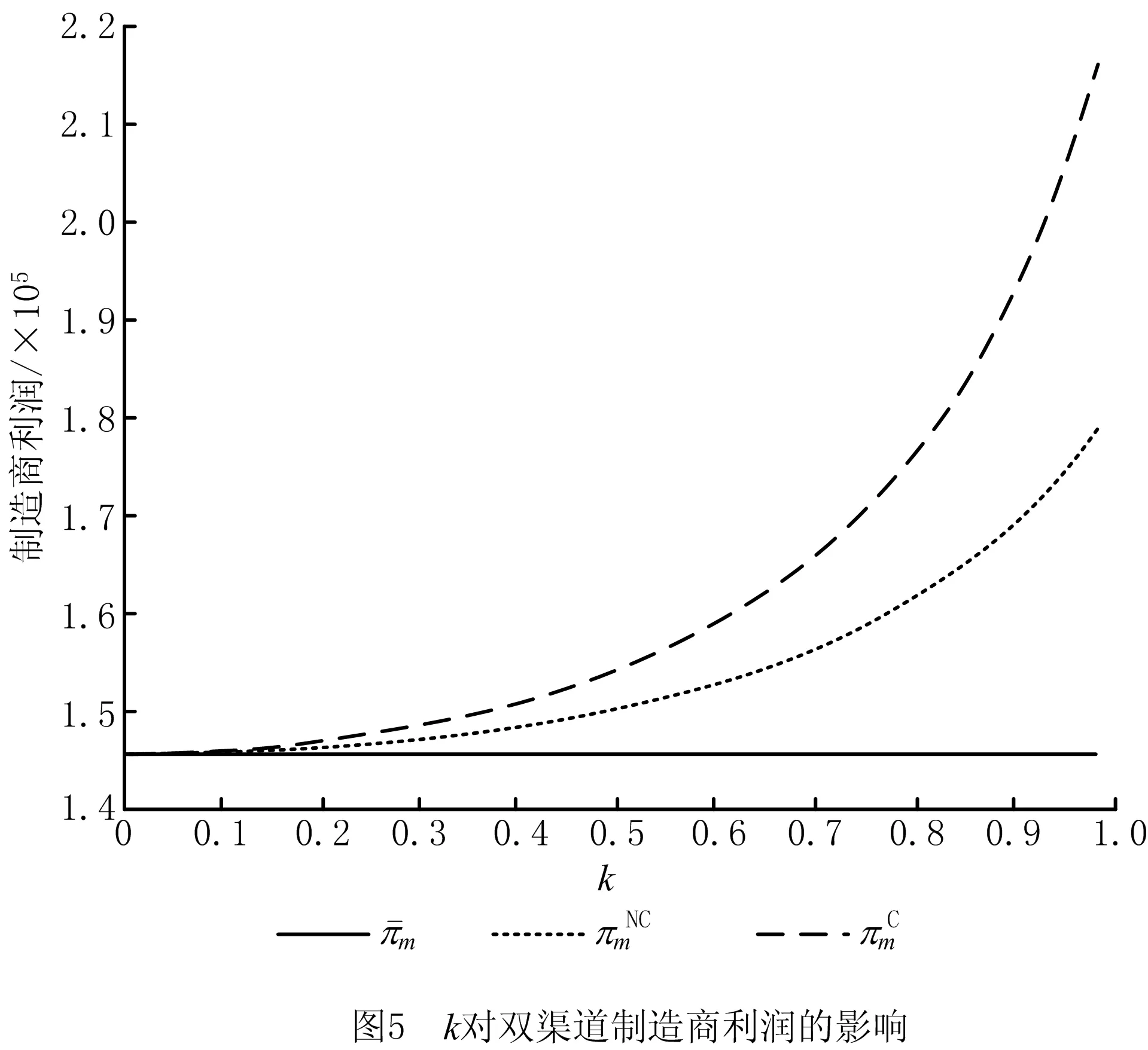
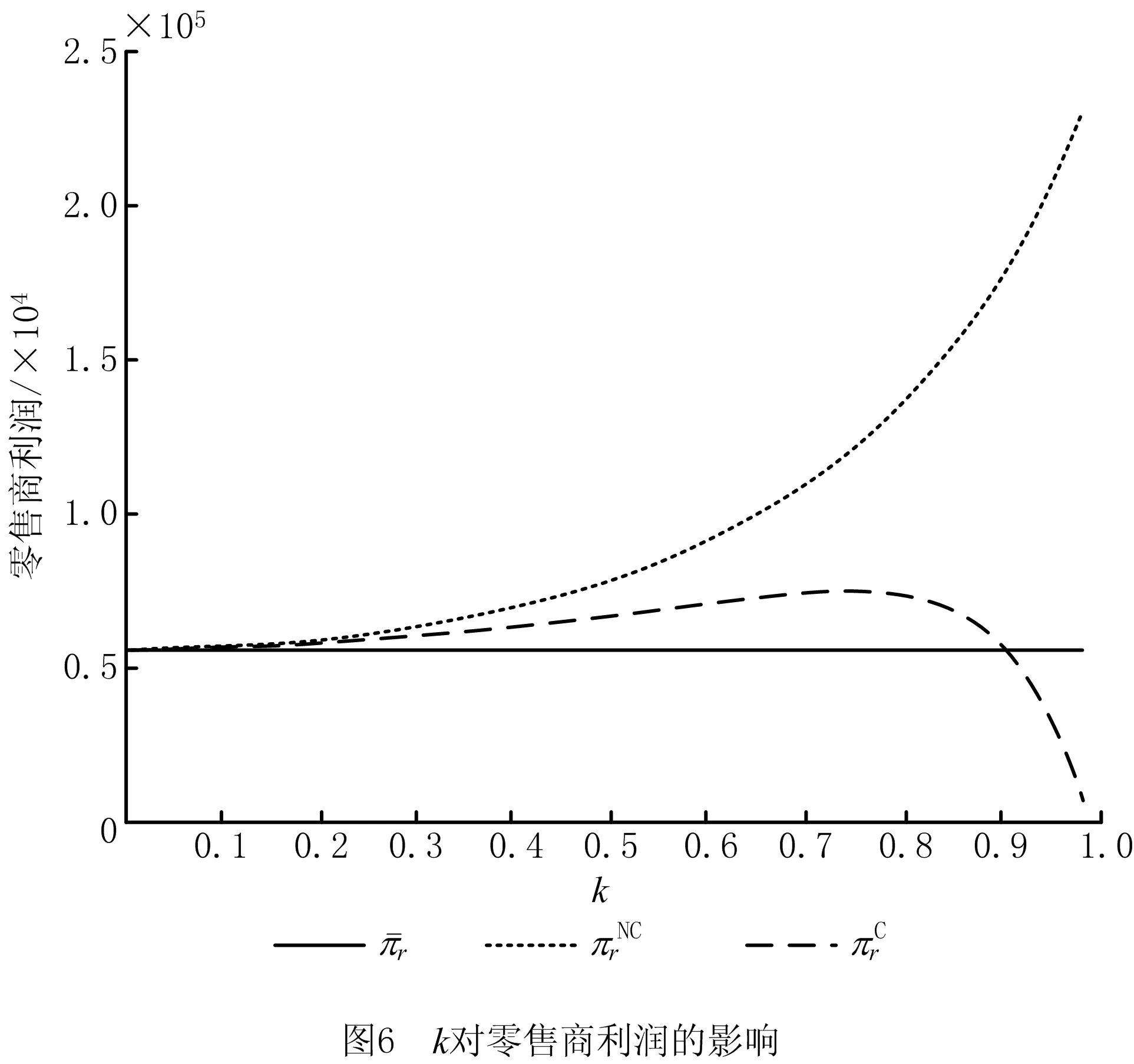
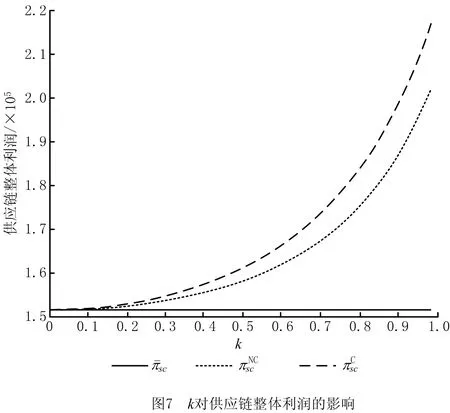
4.3 零售商广告活动对各方利润的影响分析
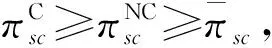
5 结束语
