初中数学教学中数形结合思想的应用

向莉文

摘  要：随着新课标的普及，初中数学教育职能发生转变。普及知识固然重要，更重要的是发展能力。从目前情况来看，教育目标并未实现。原因无他，教学方法过于老旧。为了让学生有一个好的发展，需要创新教育教学。本文结合笔者的自身的教学经验，探讨如何在数学课堂上有效应用数形结合思想，仅供参考。

关键词：初中数学;数形结合;应用策略

初中是培养数学核心素养的关键时期，教师作为领路人，理应担负起职责。但事实并非如此，很多教师一心抓进度，无暇开展创新工作。长时间使用一种方法，会严重削弱学生的学习积极性。学习动力不足，结果自然差强人意。要想扭转眼下局面，数学课堂上有效应用数形结合思想不失为一种策略。

一、数形结合思想的应用原则

无论开展何种活动，都应遵循一定原则。应用数形结合思想，必须遵循两条原则。第一，直观性原则。在转化数学形态时，教师要借助现代教育技术，培养学生的作图能力。学生只有看到具体的图像，才能有一个直观的认识，继而找出蕴含其中的数量关系，为后续解题打下基础。第二，调动性原则。在数学课堂上，教师要一直利用数形结合方法调动学生的积极性。学生体验感增强，学习效果自然會提高。更为重要的是，学生逐渐掌握数形结合的应用方法，再面对数学习题时，就可做到游刃有余。

二、数形结合思想的应用策略

（一）应用数形结合，激发学习兴趣

（二）应用数形结合，强化知识理解

学生的成长环境各不相同，导致学习能力有高有低。学习能力低的学生，对数学知识一知半解。在应用过程中，就会频繁出现问题。要想彻底消灭问题，需要应用数形结合思想。通过调查发现，学生对函数概念了解不够深入，因此将其作为讲解重点。上课之初，教师呈现一道习题。一元二次方程ax2+bx+c=0（a≠0）有2个相异正根，请说出需要满足的条件。第一步永远是审题，通过审题能够发现，一元二次方程ax2+bx+c=0（a≠0）有2个相异正根，可以转化为二次函数y=ax2+bx+c（a≠0）的图像与x轴的两个交点都在x轴的正半轴上，也就是抛物线与x轴的交点问题。待掌握这个信息后，学生就可着手画图，如图2，并借助图像找到正确答案。经过学生不懈的努力，最终给出需满足的条件，即Δ=b2-4ac>0、ac>0、ab<0。

（三）应用数形结合，培养数学逻辑

（四）应用数形结合，提高解题能力

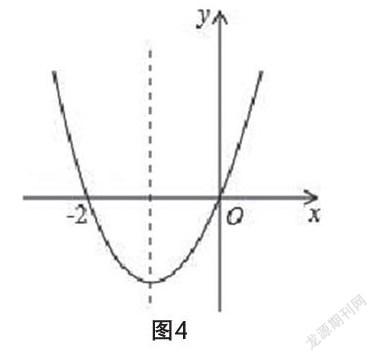
只有有效应用，才能体现数形结合思想的价值。在习题课上，教师要鼓励学生使用此法。当然，一口吃一个胖子的想法有点不切实际，要一步步来。比如，在复习二次函数时，就可举出这样的习题。y=ax2+bx+c（a≠0）是一个二次函数，其图像如图4所示。根据已有条件，判断出三种说法的对错。说法一：c=0。说法二：x=-1是函数的对称轴。说法三：x取1时，y值为2a。

在拿到题目后，学生要认真审题。待清楚题意后，即可开始作答。经过学生的验证，只有说法三是错误的。此时，教学并未结束，教师要让学生展示验证过程。当产生认知冲突后，师生要积极讨论。通过此举，让学生掌握数形结合的正确使用方法。

数学源自生活，并作用于生活。教师要往习题中注入数形结合思想，能够提升学生解决实际问题的能力。 我在《有理数的运算》 教学过程中组织学生进行了一次数学活动， 通过活动逐渐渗透数形结合思想。 笔者在黑板上绘制一条数轴， 将粉笔点在数轴的原点处， 先依照数轴正方向移动三个单位的长度， 之后“笔锋一转”， 再向反方向移动两个单位长度， 这时粉笔便停在“1” 的位置上。 此时，笔者引入有理数的加减法运算， 让学生计算 3+（-2） =？， 这时候同学们不用计算便可以非常形象地看出来， 其结果等于“1”。 通过形象的方式， 学生感受到在粉笔的两次移动过程中点的运动方向和移动距离对应的实际移动效果， “数” 和“形” 在学生的头脑中产生激烈的碰撞， 有理数的运算自然在学生的头脑中形成形象的几何解释。

三、总结

数形结合思想的引入，能够显著提高教学效果。当然，要想获得这个结果，需要教师掌握正确的方式方法。在学习函数时，应用数形结合，调动学生的学习积极性。在学习几何时，引入数形结合思想，有助于数学逻辑的形成。在讲解概念时，融入数形结合思想，能够加深学生理解。在面对习题时，采用数形结合方法，能够帮助学生找准数量关系，进而找到解决办法。

参考文献：

[1]白辉.数形结合思想在初中数学教学中的渗透[J].科学咨询（教育科研），2020（04）：220.

[2]马双平.数形结合在初中数学教学中的运用分析[J].科技资讯，2020（11）：155-156.

[3]杨玉香.浅谈初中数学数形结合思想教学[J].科学咨询（教育科研），2019（05）：115.