问题导向精准施教

徐波

摘  要：本节课以问题链的形式组织教学，体现了基于情境、问题导向的教学理念，课堂结构鲜明、一气呵成. 执教教师能够准确理解教材意图、精准施教. 特别重视落实对学生进行数学学习一般方法路径的学法指导，重视发挥“类比”作为一种思维工具的作用，仔细地处理“特殊与一般”“分类与整合”的关系，设计的课堂小结与作业注重开放性、延伸性，反映出教师树立了正确的教学观、师生观.

关键词：类比;一般路径;学法指导;特殊与一般;问题链

本节课执教教师所教授的是人教A版《普通高中教科书·数学（必修）》（以下统称“新教材”）第二册第六章第二节“平面向量的运算”中的内容，与《普通高中课程标准实验教科书·数学4（必修）》（以下统称“旧教材”）相比，在内容的安排顺序上有了一定的调整变化. 执教教师比较准确地捕捉到了新教材中的这些变化，以及这些变化所折射出来的教学含义，精心设计并实施了本节课的教学. 从课堂教学实录来看，教学效果是很好的.

一、准确理解教材意图、精准施教

与旧教材相比，新教材把向量的数量积放到“平面向量的运算”這一节中，这就暗示教学要把数量积纳入到向量运算的大家庭中，按照学习数学运算的一般方法与路径来进行学习. 而且新教材增加了一个向量向另一个向量的投影变换，投影的概念也改变了. 这是为了促使学生体会投影是构建高维空间与低维空间之间联系的桥梁，体会“特殊情况”与“一般情况”的相互作用.

同时，以此建立投影与数量积运算规则之间的关系，为后续学习向量数量积的运算律做铺垫，提升学生的直观想象、逻辑推理素养. 执教教师比较准确地解读了新教材中的这些变化，及其所透露出来的教学启示，理解到位、施教准确，很好地达成了本节课的教学目标.

二、重视落实数学学习一般方法路径的学法指导

这节课结合教学内容全面而近乎完美地呈现了数学学习的一般方法与路径，精心设计并实施了对学生的学法指导. 从课堂上学生的学习表现来看，学生已经非常清楚对“平面向量”这样一个全新的数学对象，应该从哪些方面沿着怎样的路径开展学习. 执教教师很好地处理了“授之以鱼”与“授之以渔”的辩证关系，使学生在“学会”的同时也“会学”. 因此，所达到的教学目标是丰富的、全方位的，这与执教教师的教学理念站位高远有很大的关系.

本节课是这样体现和落实这一点的.

问题1：前面我们学习了与向量有关的什么运算？

问题2：你能总结研究向量运算的主要路径吗？

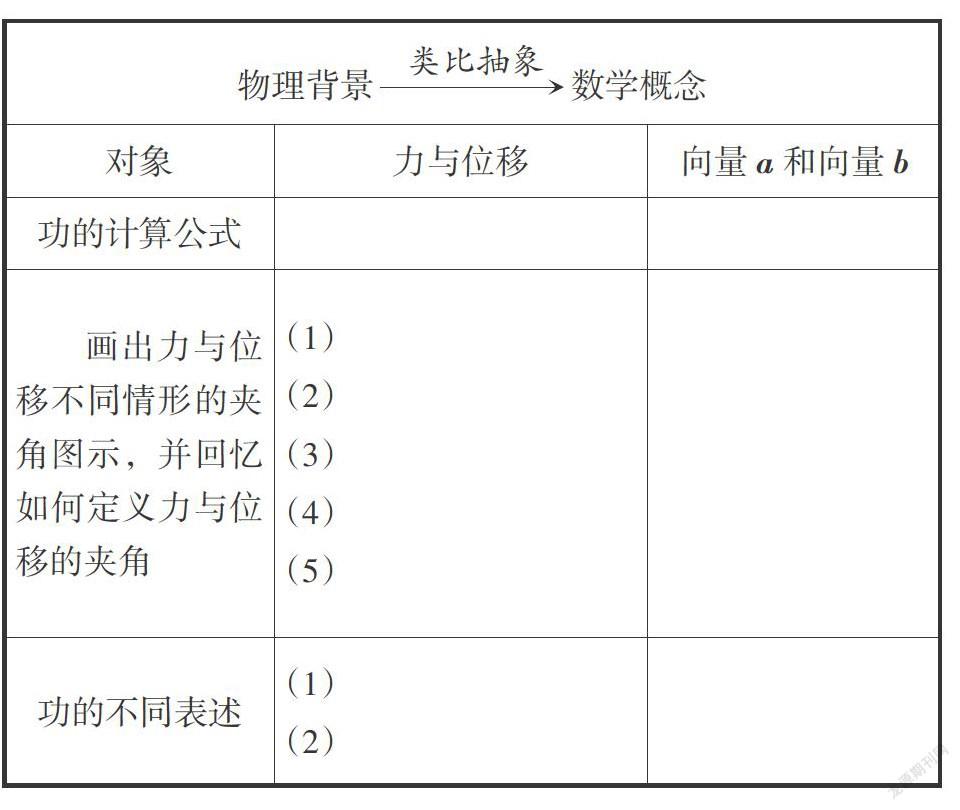
问题3：在下表中填写与“功”有关的物理问题并思考. 根据表中的物理背景，结合前面所学的向量知识，你能抽象出哪些与向量有关的数学问题？

这样就紧紧扣住了研究一个新的数学对象的一般方法与路径，结合具体的学习内容将学法指导落到了实处.

三、重视发挥“类比”作为思维工具的作用

执教教师紧紧抓住了“三个类比”作为思维工具，将这节课组织了起来，使得整堂课“聚精会神”，不仅“神不散”，而且“形也不散”.

这三个类比是：类比数的运算;类比之前学过的向量的线性运算;类比物理的背景.

从学生在课堂上的学习表现来看，学生已经很熟悉类比思维，能够驾轻就熟地运用类比思维去思考、解决问题，尤其是在类比物理背景方面. 例如，当学生面对“你认为应该如何规定零向量与其他向量的数量积？”“功还有哪些不同表述？数量积呢？”等问题时，表现得非常自如. 可见，“类比”已经内化为学生的思维工具，学生达到了能够自觉应用的程度. 这同样是与执教教师在之前的教学中理念深刻、站位高远是分不开的.

四、重视处理“特殊与一般”“分类与整合”的关系

本节课紧紧抓住了那“五张图”，也就是锐角、钝角、直角、零角、平角这五种情况. 先从思考锐角的情形出发，然后再去考虑钝角、直角、零角、平角的情形，达成了结果在形式上的统一，最后概括，形成概念或者结论. 以此来培养学生缜密的思维，发展学生归纳概括的思维素养，将数学课程的育人价值落到实处.

本节课也特别关注了零向量. 例如，在规定两个向量的夹角时是不包括零向量的，但是在定义两个向量的数量积时又是包括零向量的，在定义一个向量在另一个向量上的投影时也是包括零向量的. 这种对零向量的特别关注，给学生留下了深刻的印象.

从学生在课堂上的学习表现来看，在上课过程中学生能始终关注到零向量，在课堂小结环节谈学习体会时，学生也谈到了思考问题要全面、不要漏掉特殊情况等. 因此，从这个方面也可以看到了数学课程的育人价值的落实情况.

五、重视对课程标准的研读和新课程理念的落实

问题链教学是这节课的灵魂. 本节课精心设计的8个问题所形成的问题链，对整堂课的组织结构做出了很大的贡献.

本节课主要是以问题链的形式组织教学，体现了基于情境、问题导向的教学理念，将启发式、互动式、体验式等课堂教学方式融为一体，整堂课一气呵成、畅快淋漓，展现了执教教师过硬的组织课堂教学的功底.

本节课充分体现了执教教师对《普通高中数学课程标准（2017年版）》（以下统称《标准》）的研读和新课程理念的落实，对学生的数学学科核心素养的发展多有关照，对培养学生的“四基”“四能”不遗余力. 本节课涉及可以促进学生发展的数学学科核心素养有：数学抽象、逻辑推理、数学运算、直观想象. 执教教师在做“教学策略分析”时谈到“充分重视学生基本数学活动经验的习得，创设合适的教学情境，尽可能给学生更多的空间和时间，去亲身经历、亲自体验、亲手实践，在教师的引导下，让每个问题通过思考、交流由学生自己解决”，而且我们看到在课堂教学中执教教师也确实是这样做的. 学生在课堂学案上各自独立完成画图和练习，学生在黑板上展示自己的结果和思路，尤其是执教教师安排学生互相点评发表观点，这其实是深度学习的表现，这都反映出执教教师树立了正确的教学观、学生观.

问题链教学最难把握的就是一个“度”，《礼记·学记》中写道：“道而弗牵，强而弗抑，开而弗达”，说的就是这个道理.

六、重视设计开放性的小结与作业

在课堂小结和作业环节，执教教师并没有按照传统的教学方式去做，而是体现了自己的独立思考和创新. 例如，“回顾得出数量积定义的探究过程和研究思路，并表述研究方法，在这个过程中自己的贡献和收获是什么？”“类比向量运算的研究脉络，你知道接下来我们还需要进一步探究数量积运算的哪些问题吗？”“依据数量积公式能够实现‘知三求一’的问题，各学习小组自编6道不同角度的问题并规范解答，下节课各小组互相竞答板演”等. 不落俗套，这反映了执教教师为落实《标准》付出的努力.

任何数学概念都具有“过程”与“对象”的两重性，本节课比较强调向量的数量积作为“过程”的一面，而作为“对象”的一面就稍弱些，可能是由于这是第一节课. 相信在接下来的课程中向量的数量积作为“对象”的这一面会得到加强和沉淀，以达到“过程”与“对象”的平衡.

参考文献：

[1]中华人民共和国教育部制定. 普通高中数学课程标准（2017年版）[M]. 北京：人民教育出版社，2018.

[2]曹才翰，章建跃. 数学教育心理学[M]. 北京：北京师范大学出版社，2006.