采用双异质群体演化博弈的网络安全防御决策方法

2021-09-10张恩宁王刚马润年伍维甲严丽娜

西安交通大学学报 2021年9期

张恩宁,王刚,马润年,伍维甲,严丽娜

(1.空军工程大学信息与导航学院,710077,西安;2.国防科技大学信息通信学院试验训练基地,710106,西安)

5G和区块链等信息网络技术加速了信息化向智能化发展的步伐,与此同时,以高级可持续威胁为代表的隐蔽、高效和针对性网络攻击使得网络安全态势和防御决策日趋复杂[1]。网络安全防御决策是网络防御技战术运用的前提和关键环节,建立在对网络攻防行动特点和网络业务负载动态需求等要素的准确掌控上[1]。在现实环境中,网络态势信息的不完整性和决策者的有限理性使得网络攻防双方很难完全知悉对手的准确实时信息,在不完全信息条件下,攻防双方认知和决策模式的不同,导致攻防行为的差异性和攻防决策的异质群体演化博弈特征[2]。

演化博弈中的群体源于生物学中的种群概念。生物学中,同一物种的不同种群因为生存环境的不同而存在性状上的差异,在研究过程中需要将对象区分为异质种群。在学术领域,生物学中的种群映射为博弈理论中的群体,不同群体在博弈中代表的是属性类型相同但决策方式不同的博弈参与方。在一些网络攻防博弈情境中,博弈双方可设定为有限理性博弈参与者,但是其决策方式存在一定差异性。例如,在决策标准方面,防御方要权衡防护节点的资源重要程度,安防部署成本和防御操作代价,而攻击方则需要考虑攻击成本、攻击收益等因素[3]。因此,设定博弈参与方采用相同决策方式的传统演化博弈本质上属于同质群体演化博弈。相对而言,异质群体演化博弈能更好地体现出博弈参与方不同的决策方式对博弈均衡的影响,依据攻防双方收益函数不同的网络攻防博弈,属于双异质群体演化博弈。

决策差异性是网络攻防博弈中需重点关注的问题。对于具体决策,网络攻防双方很难完全知悉对手的准确实时信息,决策的可信度相对不足,攻防双方认知和决策模式的不同,同步导致攻防决策的差异性,这种差异性客观上使得基于防御方收益信息的预测分析很难实现精确性决策[3]。此外,对于决策者和执行单元,单次防御行为应是确定性的和基于纯策略的,经典纳什均衡解固有的多重性使得策略取舍成为网络攻防博弈决策的难题,基于智能算法的网络防御混合策略无法从根本上解决这一问题[2]。

博弈论和行为经济学中对于参与人目标对立、策略依存和非合作型关系的建模符合网络对抗的基本特征规律[4-5]。零和博弈、信号博弈、微分博弈、贝叶斯均衡博弈、马尔可夫博弈及演化博弈等模型被相继运用到网络攻防对抗的行为建模中[6-9]。其中,演化博弈模型可以在不完全信息条件下模拟网络攻防双方策略的互动演化过程,得到稳定的纳什均衡策略,为优选网络防御策略提供参考[10]。目前,相关研究主要集中在3个领域。一是演化博弈模型对决策的动态影响。在多阶段博弈中,有限理性的博弈双方会根据初始博弈信息改变策略选择倾向,最终达成混合策略的纳什均衡。文献[11]建立了物联网系统多级非对称信息攻防模型,分析了进攻型策略和防御型策略的收益变化;文献[12]结合现实生活中银行现金转运案例,建立多目标混合遗传算法,得到距离和风险最小化、利润最大化、车辆油耗最小化、时间最小化或最大化等多种目标下的演化博弈最优混合策略,对多目标网络安全防御决策具有很高的参考价值。二是环境对演化博弈模型中系统动力学方程的影响,结合实际环境改进复制动态方程,提升模型的精确性。文献[13-14]针对攻防博弈系统中存在各类随机干扰因素的问题,借鉴高斯白噪声的概念,建立随机复制动态微分方程,分析了系统环境、策略变化等各类随机干扰因素对攻防策略选取演化速率和倾向的影响;文献[15]考虑同一博弈方之间策略的相互影响,引入激励系数,改进传统复制动态方程,完善复制动态速率计算方法,分析了同一博弈方之间策略的促进和抑制作用;文献[16]引入学习机制和第三方惩罚机制,构建了网络攻防演化博弈系统动力学模型,发现通过第三方监管部门,采取对攻击者收益的动态惩罚策略,对攻防双方的恶化混合策略的偏移有重要影响。三是策略的可行性和决策方法。传统演化博弈模型得到的演化均衡解是混合策略,现实中以概率形式进行防御策略选取并不可取,以纯策略为基础进行决策更符合客观规律[17]。文献[18]结合动态目标防御理论,使用精炼贝叶斯均衡求解算法和先验信念修正,提出移动目标防御策略的跳变周期、差异性和先验知识是影响决策效果的3个关键因素;文献[19]将多阶段演化博弈和马尔可夫决策方法相结合,提出多阶段多状态下最优防御策略选取方法;针对复杂网络中攻击方和防御方可用资源的差异性,文献[20]提出了复杂网络拓扑结构对策略选择的制约影响关系。

随着近年来网络攻防技战术的快速发展和实践应用,网络安全防御决策领域凸显了一些新的难题:①决策主体的差异性和基于主体差异性的防御行为模式突破了经典研究中对攻防博弈双方均为同质群体的假设,需要克服基于这种假设导致的最优防御策略事实偏差;②现实多阶段博弈中的防御决策,应充分考虑经验的参考价值和决策行为的智能化需求,在决策过程中引入反思机制和对应的可信支撑模型;③网络安全防御单次决策的确定性需求和传统纳什均衡解的局限性存在固有矛盾,传统纳什均衡解的多重性和混合纳什均衡的不确定性无法满足单次决策中防御行为的可行性要求,需要从模型求解等方面寻求新的突破。

针对这些问题,本文开展了基于异质群体演化博弈的决策方法研究。结合生物学中的种群概念,在博弈中将攻防双方区分为不同群体,提出双异质群体演化博弈模型,克服经典模型中最优防御策略的事实偏差。引入策略反思机制,将博弈主体对于博弈历史经验反馈模型化,改进复制动态方程以提升演化结果的精确性。在模型中引入势函数,突破传统纳什均衡解的局限性,使模型解稳定收敛于可行策略,满足网络安全防御决策的确定性需求。最后,通过理论分析和仿真,验证了所提模型和决策方法的有效性和先进性。

1 双异质群体演化博弈模型构建

1.1 双异质群体演化博弈模型

基于博弈双方决策行为标准的差异性分析,引入生物学种群概念,将攻防双方区分为不同博弈群体,参考经典演化博弈模型的定义[14-15],提出了网络安全防御的双异质群体演化博弈模型。

定义1网络攻防博弈是对称博弈,所有博弈参与者根据其自身属性分为网络攻击方和网络防御方。

定义2网络攻防博弈是多阶段博弈,在后一阶段,每个博弈参与方对前一阶段的博弈策略进行模仿。在每一个阶段,博弈参与方的自然出生率为β(β≥0)、自然死亡率为δ(δ≥0),以此代表博弈参与方对于该阶段环境的适应性,即网络攻防双方在阶段前和阶段中因断网掉线等不可抗因素退出博弈的概率。

定义3将生物学中的概念映射到博弈模型中。博弈模型中群体代表同一类别个体的集合,即种群。子群体代表具有同样特征的个体的集合,即具备同样性状的个体集合,子群体隶属于群体。

定义4每一阶段的博弈是从每个博弈方子群体中随机抽取一个人进行博弈。

定义5双异质群体演化博弈模型可表示为4元有序组(N,S,P,U),其中N=(N1,N2,…,Nm)为异质群体参与者空间。

结合定义1,可设定N=(NA,ND)。其中:NA是攻击方参与者总空间,NA=(NA1,NA2,…,NAj),NA1,NA2,…,NAj是攻击方参与者子群体;ND是防御方参与者总空间,ND=(ND1,ND2,…,NDi),ND1,ND2,…,NDi是防御方参与者子群体。

S=(SA,SB)为攻防博弈参与者群体的混合策略空间。其中:SA是攻击方参与者纯策略总空间,SA=(SA1,SA2,…,SAj),SA1,SA2,…,SAj是攻击方参与者子群体选择的纯策略;SD是防御方参与者纯策略总空间,SD=(SD1,SD2,…,SDi),SD1,SD2,…,SDi是防御方参与者子群体选择的纯策略。

P=(PA,PD)为博弈信念集合。其中:PA是攻击方博弈信念集合,PA=(PA1,PA2,…,PAj),PAj是选择策略SAi的概率;PD是攻击方博弈信念集合,PD=(PD1,PD2,…,PDi),PDi是选择策略sDi的概率。

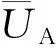
演化博弈是多阶段的动态博弈过程,每一个阶段的博弈结果都会对后一阶段的博弈产生影响。结合定义2和4,t时刻子群体NDi(t)的时间导数为

(1)

结合博弈信念集合定义,可得在任意时刻t有

PDi(t)ND(t)=NDi(t)

(2)

式(2)两边同时对t求导,整理可得

(3)

1.2 关键参数与收益计算

参照文献[17-18]的攻防收益计算方法,定义本文中收益量化的关键参数和计算公式。

定义6资源重要程度Cr,指在一次完整的攻防过程中,攻击方目标资源的重要程度。

定义7操作代价Ocost,指防御方为使攻击方攻击无效做出针对性调整所需付出的代价。例如,系统开销增大、服务质量下降等。

定义8攻击成本Acost,攻击者进行攻击时所付出的代价。例如,攻击的时间成本、风险成本等。本文中攻击成本与漏洞的威胁级别有关,漏洞的威胁级别越高,攻击成本就越低。

定义9感染概率λ,指攻击方成功利用漏洞感染防御方的概率。

定义10防御效果γ,指防御方利用防御动作成功清除病毒的概率。

结合定义6～10可知,某一阶段博弈中,防御方的收益可表示为

UD=γCr-Ocost

(4)

攻击者收益源于感染平台后得到的收益,与感染概率有关。攻击收益可表示为

UA=λCr-Acost

(5)

2 改进复制动态方程和决策方法

2.1 策略“反思-学习”机制

在多阶段博弈中,博弈双方通常不会满意当前阶段博弈策略的收益,认为存在更优策略。在这种假设下,博弈双方会寻求其他策略进行学习,在下一个阶段博弈中采用新的策略,这也就是策略“反思-学习”机制[2]。显然,现实网络攻防博弈决策本质上应是基于“反思-学习”机制的。在每一阶段博弈结束后,攻防双方的每一个子群体,都从群体中随机抽取一个其他子群体作为反思对象进行策略学习。这种“反思-学习”机制可结合建模分析,建立与之相一致的演化博弈模型和系统动力学方程。在有限理性条件下,网络攻防子群体基于“反思-学习”机制的策略调整行为,可视为独立的累计随机事件发生次数的增量过程,即泊松过程[2]。子群体的“反思-学习”时间可近似为泊松过程的到达时间,泊松过程到达率即为平均反思率Rs。假设子群体的泊松分布在统计上是相互独立的,则采取防御策略SD的子群体“反思-学习”时间之和是一个泊松过程,其到达率为

Parrive=PDiRs(NDi)

(6)

(7)

根据大数定律,设群体随机过程为确定性的流,则子群体NDi来自选择防御策略SDj的子群体NDj的流入Pin为

(8)

子群体NDi的流出Pout为

(9)

防御策略的博弈信念PDi变为

(10)

若群体中策略不成功的子群体的反思率高于策略更成功的子群体的反思率,就会出现收益严格单调递减的选择动态。引入ρ(x)[2],设势函数ρ(x)在其自变量x上严格单调递减,则平均反思率表示为

Rs(NDi)=ρ(UDi)

(11)

防御策略SDi的选取概率PDi可表示为

(12)

设子群体的反思率在其当前收益上是线性递减的,则

ρ(UDi)=a-bUDi(a,b∈R)

(13)

设反思率Rs(NDi)非负,则

(14)

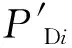
2.2 最优防御纯策略选取方法设计

按照2.1小节的防御决策理论,结合网络安全防御行为特点,设计最优防御纯策略选择方法,伪代码如下。

输入:双异质群体演化博弈模型

输出:最优防御纯策略SDi

BEGIN

1 初始化P,U,S,b;

2 定义T,function;

3 for (k=1;k≤T;k++)

6 ode45(function,T,P);

7 WhenPDi=1

8 ReturnSDi;

9 Else

10 Return 0;

11 end

END

本文方法对应的时间复杂度为O(k(m+n)2)。在实际网络攻防中,博弈参与方的数量增加只会导致相应的攻防策略数量也增加,该方法复杂度仍处于同一量级,理论上能够满足网络攻防的时敏需求[17]。

2.3 模型及方法对比

对照文献[11,15-17],从博弈类型、复制动态速率准确性和策略选取应用价值共3个方面分析本文模型和决策方法,结果如表1所示。

表1 相关工作比较

在博弈类型方面,文献[11,15-17]均以同质群体演化博弈理论为基础,不能体现出攻防双方差异性。在复制动态速率准确性方面,文献[11,16]考虑不完全信息条件,结合动态演化思想,突破传统演化博弈模型单阶段完全信息博弈的局限性,提出使用系统动力学方程来表示过程的动态演化特点,至于策略之间的相互影响还有待进一步挖掘。文献[15]引入激励系数刻画同一博弈方之间的策略激励与抑制作用,但并未能给出激励系数的求解过程。在策略选取应用价值方面,文献[11,15]并未区分纯策略和混合策略在实际应用中的价值高低,文献[16]考虑了第三方惩罚策略对防御策略选取的影响,但第三方惩罚策略有其自身局限性,一定程度上降低了模型求解的稳定性。文献[17]结合军事信息网络特点,给出了军事信息网络最优纯策略的选取办法,满足了网络安全防御确定性决策的需求,但是有待进一步研究可行策略的稳定性问题。

对比分析表明,所提模型和决策方法考虑攻防双方的差异性提出了双异质群体演化博弈模型,改进复制动态方程以提升模型求解的准确性,求解稳定可行的纯策略提升了策略的实际应用价值。

3 稳定性分析

3.1 数理证明

首先引入演化稳定和最优策略集合的定义。

定义11对于博弈参与方的不同混合策略Sx、Sy,若存在εy∈(0,1)满足不等式U(Sx,Sω)≥u(Sy,Sω)对所有的ε∈(0,εy)都成立,那么Sx是演化稳定策略。其中,Sω=εSy+(1-ε)Sx是混合策略Sy入侵原有混合策略空间后形成的新混合策略,Sy是入侵策略Sy在博弈中的被选取概率,U(Sx,Sω)是原策略空间被策略Sy入侵后的收益,U(Sy,Sω)是入侵策略的收益。

定理1异质群体N演化稳定的充要条件是N存在严格纳什均衡。

(2)必要性。设异质群体N存在严格纳什均衡,固定博弈参与者在博弈总空间中的位置为Ni且令Sy≠Sx。对于任意i有U(Sxi,S-xi)=U(Sxi)>U(Syi,S-xi),由于收益U(Sxi)是连续函数,必存在εy∈(0,1)使得对任何ε∈(0,εy)和Sω=εSy+(1-ε)Sx都有U(Sxi,S-ω)>U(Syi,S-ω),即异质群体N是演化稳定的。证毕。

由定理1的分析证明可知,Rs的形式决定了方程是否有渐进稳定的演化均衡解。博弈模型中,不稳定的演化均衡解无法形成可行可信的优选策略。因此,引入势博弈和势函数概念[21],即如果每个子群体的策略改变是单调的,并且能够映射到一个全局单调函数中,则这个全局单调函数就是势函数,此类博弈必存在严格纳什均衡。因此,将势函数引入式(12)可以使异质群体演化博弈模型得到演化稳定解,从而实现防御的有效精确决策。

引理1每个势博弈均有纯策略演化稳定解。

异质群体参与者空间N=(N1,N2,…,Nm),函数ρ是异质群体博弈的势函数,因此Ni的演化稳定解可映射到N(ρ(i))中,当且仅当U(ρ(i))≥U(-ρ(i))时成立。由于势函数单调,因此N(ρ(i))存在纯策略演化稳定解,Ni存在纯策略演化稳定解。

3.2 算例分析

以2×2攻防对称博弈为例,演绎演化均衡解求解过程。攻防双方各含有两个子群体NA1、NA2,ND1、ND2,对应纯策略为SA1、SA2,SD1、SD2。以博弈防御方为例,收益矩阵可以表示为

(15)

式中:D是标准化矩阵,减少了需要观察的变量数;u1是攻击方采取纯策略SA1时防御方采取纯策略SD1获得的相对收益;u2是攻击方采取纯策略SA2时防御方采取纯策略SD2获得的相对收益。将u1、u2代入式(14),可得对应防御方和攻击方的复制动态方程

(16)

运用MATLAB分析博弈演化稳定解的稳定性。由式(15)可知:u1、u2的正负会影响博弈的演化趋势,u1、u2的数值不影响博弈的演化趋势;b的数值会影响博弈的演化速率。实验中,对u1、u2及b的取值进行多次调整,发现并不影响演化稳定解的收敛结果。参考文献[10],设定|u1|=0.4,|u2|=0.6,b=1,初始博弈信念PA1、PD1为(0,1)间的随机数。图1为500次蒙特卡罗仿真实验得到的本文模型演化稳定解的收敛轨迹。图中,蓝色标记点是纯策略解收敛点,红色标记点是混合策略解收敛点。

分析图1b和1d可知:当u1u2<0时,博弈信念在状态空间内不改变符号,从状态空间内部任意初始位置开始,博弈双方的总体状态都会收敛到严格占优纯策略,即当u1=0.4、u2=-0.6时,攻击方采取纯策略SA1,防御方采取纯策略SD1;当u1=-0.4、u2=0.6时,攻击方采取纯策略SA2,防御方采取纯策略SD2。

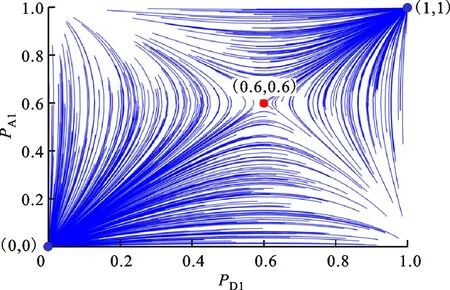
(a)u1=0.4,u2=0.6

(b)u1=0.4,u2=-0.6

(c)u1=-0.4,u2=-0.6

(d)u1=-0.4,u2=0.6图1 本文模型演化稳定解的收敛轨迹Fig.1 Converging tracks of evolutionary equilibrium of the proposed model

分析图1a和1c可知:当u1u2>0时,博弈有两个严格纯策略纳什均衡和一个混合策略纳什均衡。结合式(16)可知,当博弈收敛到混合策略纳什均衡时,PA1=u2/(u1+u2),PD1=u2/(u1+u2)。博弈的混合策略纳什均衡点不稳定,会随着u1u2的变化而发生改变。因此,当u1u2>0时,博弈仅有两个稳定的严格纯策略纳什均衡。进一步分析图1a可知,混合策略纳什均衡是一个鞍点,除了通过鞍点的曲线外,其他的解轨迹都会收敛到两个稳定的纯策略纳什均衡,即当u1=0.4、u2=0.6时,攻击方采取纯策略SA1、防御方采取纯策略SD1,或者攻击方采取纯策略SA2、防御方采取纯策略SD2。进一步分析图1c可知,攻防博弈双方的博弈策略会收敛到更极端的情况,即当u1=-0.4、u2=0.6时,攻击方采取纯策略SA1、防御方采取纯策略SD2,或者攻击方采取纯策略SA2、防御方采取纯策略SD1。

对比其他相关文献可知,双同质群体演化博弈模型中,2×2对称博弈模型的混合策略演化稳定解是稳定的,可作为最优防御策略的参考[10,15],但在双异质群体博弈模型中,2×2对称博弈模型的混合策略演化稳定解是鞍点,并不是严格稳定的。这也符合实际博弈过程的特点,即当博弈发生在两个有区别的群体中时,行为上会呈现极端化的趋势,决策会越来越偏向某一种单一策略[22]。

为体现模型及方法克服事实偏差的能力,设置对比实验。经典模型中复制动态方程[2,10]为

(17)

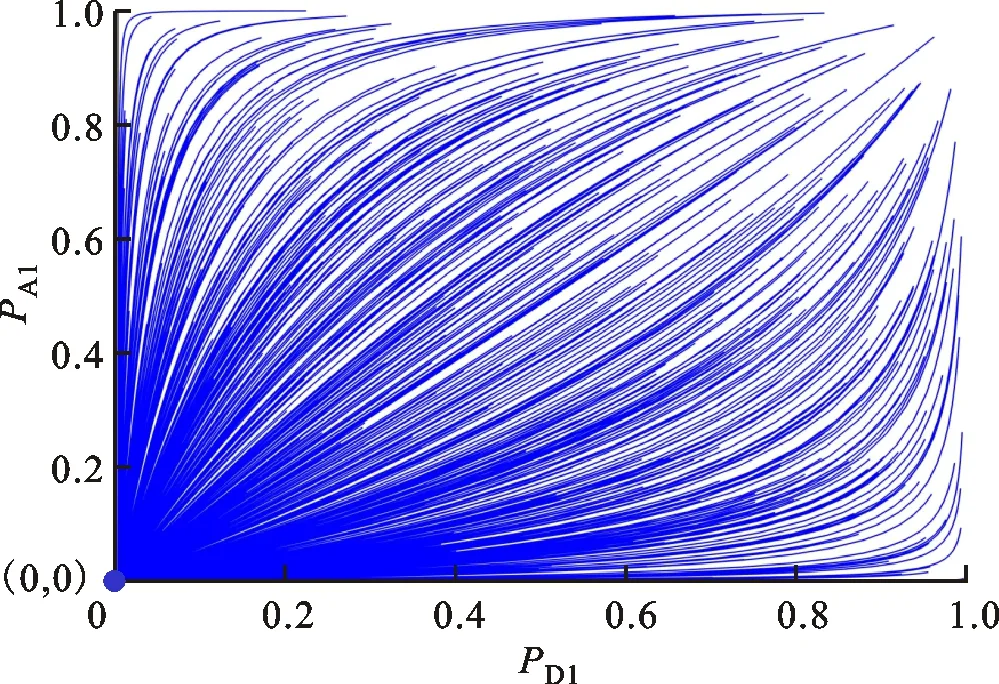
对比式(16)(17)可知,经典模型中攻防双方的策略调整并未考虑对方的博弈策略变化,而是通过自身收益变化调整策略选择。但是,现实网络攻防博弈是常和博弈,攻防双方收益的衡量方式并不相同。运用经典模型选择最优防御策略,可能会受到攻击方欺骗性策略的诱导,产生错误的策略参考结果。为证明这一点,保持|u1|=0.4、|u2|=0.6不变,初始博弈信念PA1、PD1为(0,1)间的随机数。图2为500次蒙特卡罗仿真得到的经典模型演化稳定解的收敛轨迹。

(a)u1=0.4,u2=0.6

(b)u1=0.4,u2=-0.6

(c)u1=-0.4,u2=-0.6

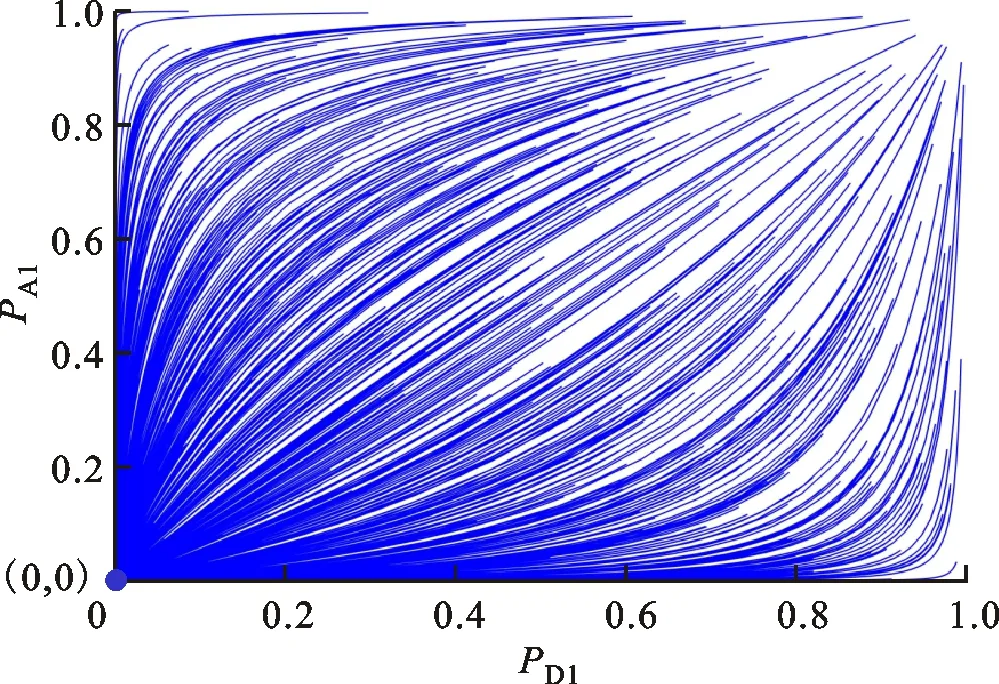
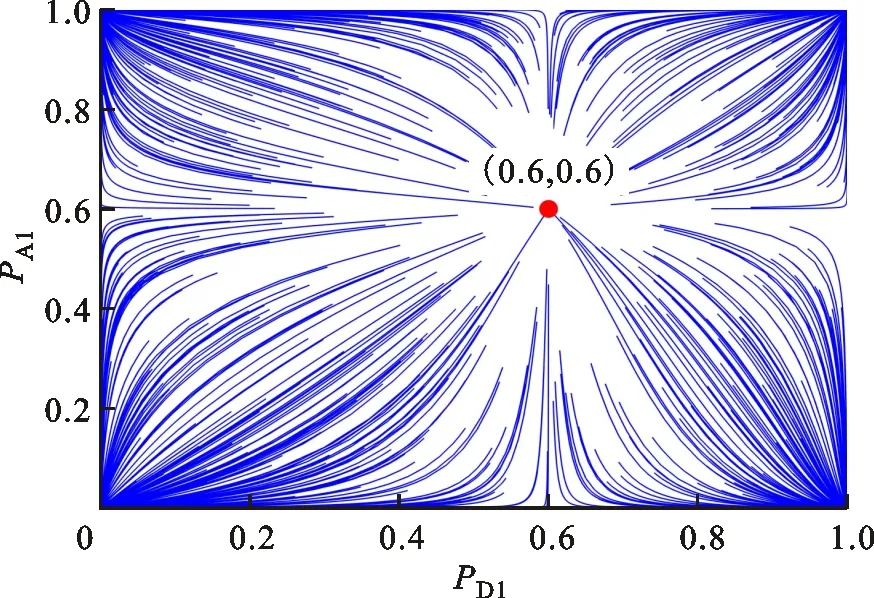
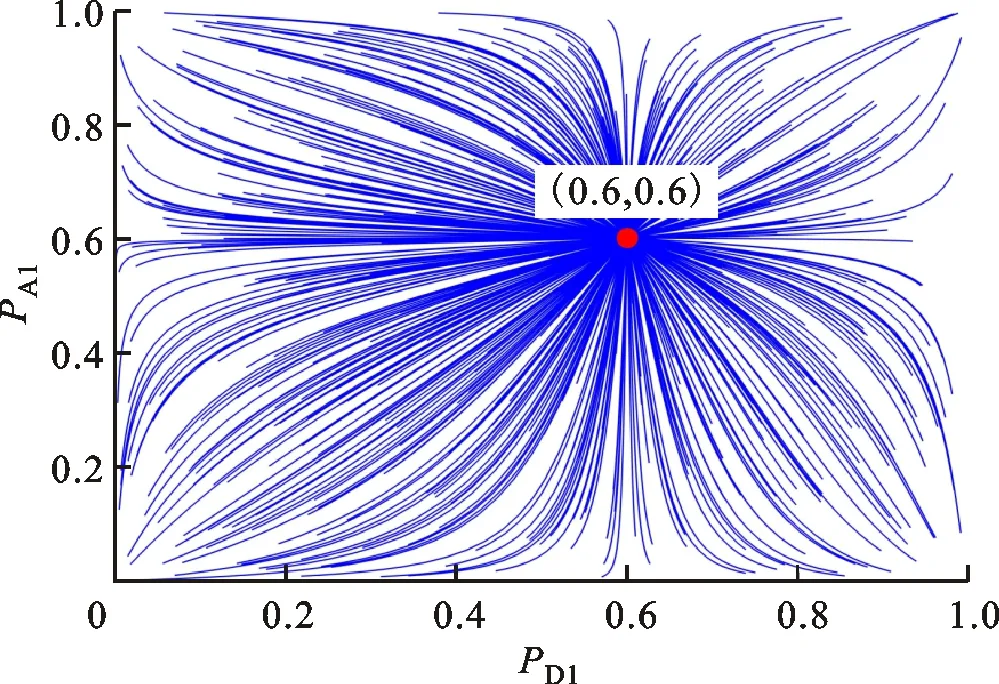
(d)u1=-0.4,u2=0.6图2 经典模型演化稳定解的收敛轨迹 Fig.2 Traditonal converging tracks of evolutionary equilibrium

分析图2a可知,当u1>0、u2>0时,博弈结果和初始博弈信念PA1、PD1的数值有关,无法实现策略的优选。分析图2c可知,当u1<0、u2<0时,博弈收敛至混合策略纳什均衡点(0.6,0.6),此时博弈结果以概率形式出现,不利于现实中决策的确定性需求。对比分析图1b、1d和图2b、2d可知,当u1u2<0时,经典模型和双异质演化博弈模型的演化稳定解相同。需要说明的是,由于经典模型中防御策略演化并未考虑攻击方博弈信念的变化,攻击方完全可以利用这一漏洞设计欺骗策略来误导防御方。综合分析可知,经典模型有50%的概率不能实现防御策略的确定性优选,相对而言,本文提出的模型及克服经典模型中同质群体假设带来的事实偏差,为网络安全防御提供可信的防御决策参考。

4 仿真分析

4.1 实验环境

借鉴经典网络信息系统设计理念和相关文献的实验设计[15,17,23],部署一个简单的网络信息系统进行仿真实验。该网络信息系统的拓扑环境见图3。

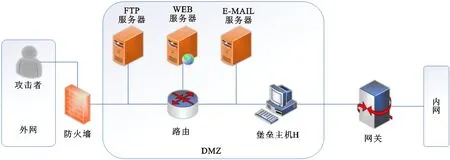
图3 网络信息系统的拓扑结构Fig.3 Topological structure of network information system

防火墙和网关将网络分为攻击方所在的外网区、实验进行的隔离区(DMZ)和防御方(用户)所在的内网区。防火墙的访问控制策略是非内网主机只能访问DMZ区的FTP服务器、Web服务器、E-MAIL服务器和堡垒主机H,DMZ区中的3个服务器都是思科服务器。使用Nessus工具扫描实验网络信息系统,结合国家信息安全漏洞库(CNNVD)提供的漏洞信息[24]及姜伟等关于网络防御策略及操作代价的定义[25],本文实验使用原子攻击策略和原子防御策略,分别如表2和表3所示。

表2 原子攻击策略

表3 原子防御策略

攻击方利用高评分漏洞进行攻击,短期内收益见效快,但不利于长期持有后收益升值(典例为零日漏洞)。选择低评分漏洞为目标,攻击成本高,单次收益低[3]。本文将利用高评分漏洞设定为冒险型进攻策略SA1=(a1,a2,a3),利用低评分漏洞设定为保守型进攻策略SA2=(a4,a5)。

防御方的策略收益主要取决于操作代价,操作代价低的防御策略往往有效性较差。因此,本文将使用高操作代价策略设为冒险型防御策略SD1=(b4,b5),使用低操作代价策略设为保守型防御策略SD2=(b1,b2)。结合收益计算式(4)(5),设资源重要程度Cr=1,可得攻防策略收益,如表4所示。

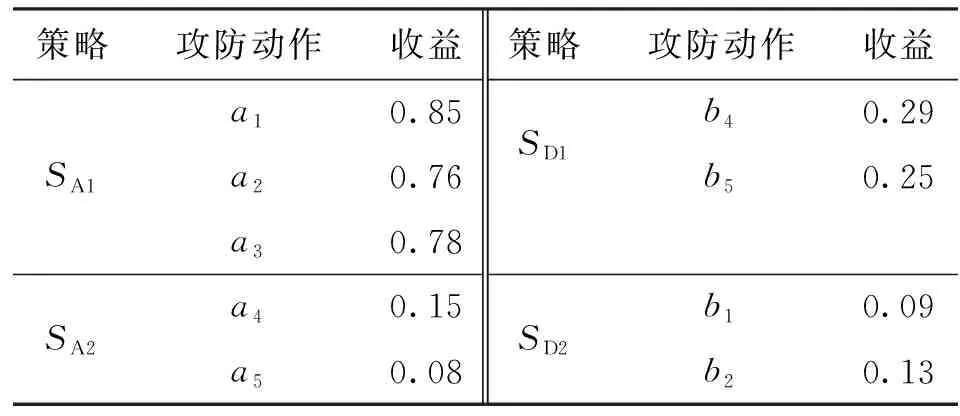
表4 攻防策略收益

计算策略收益时,认为策略收益等于策略所包含的原子攻防动作的平均收益。结合式(15),给出攻防双方的收益量化矩阵

(18)

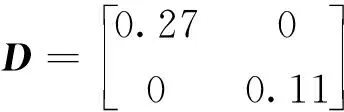
(19)

4.2 模型及算法仿真验证

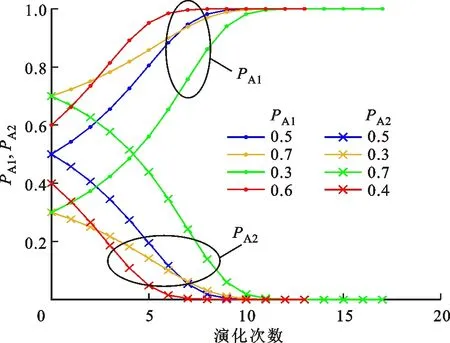
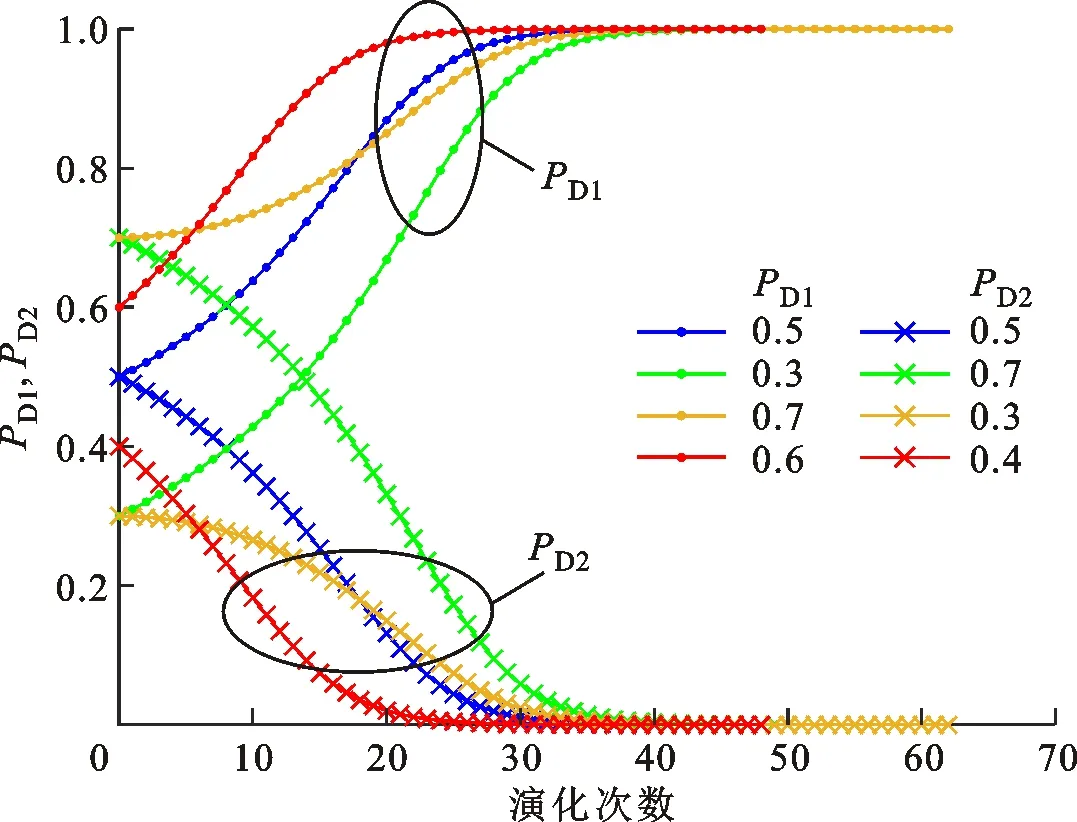
4.2.1 攻防策略选取概率变化趋势结合式(18)(19),设置控制变量b=1,研究实验条件下演化稳定策略的收敛情况。设置初始博弈信念(PA1,PD1)={(0.5,0,5),(0.7,0.3),(0.3,0.7),(0.6,0.4)}分别代表攻防双方无策略选取倾向,攻击方倾向于选取策略SA1、御方倾向于选择策略SD2,攻击方倾向于选取策略SA2、防御方倾向于选择策略SD1,攻击方倾向于选取策略SA1、防御方倾向于选择策略SD1共4种不同情况。图4给出了攻防双方策略选取概率变化趋势的仿真结果。

(a)攻击策略选取概率

(b)防御策略选取概率图4 攻防双方策略选取概率变化趋势Fig.4 Changing trend of strategy selection probability of attack and defense

分析图4a、4b可知:对应不同的初始博弈信念(PA1,PD1)={(0.5,0,5),(0.7,0.3),(0.3,0.7),(0.6,0.4)},PA1始终收敛至1,PA2始终收敛至0;PD1始终收敛至1,PD2始终收敛至0。结合实验条件A、D的数值进一步分析可知,在冒险型策略的相对收益u1远大于保守型策略的相对收益u2的情况下,无论攻防双方在博弈开始前有无策略选取倾向,网络攻防双方最终都会选择冒险型策略。

4.2.2 反思能力b对攻防策略选取的影响保持u1、u2不变,设定初始博弈信念(PA1,PD1)=(0.7,0.3),分别取b=0.5,1,1.5,研究参数b对于博弈结果的影响。图5给出了b不同取值下攻防双方策略选取概率变化趋势的仿真结果。

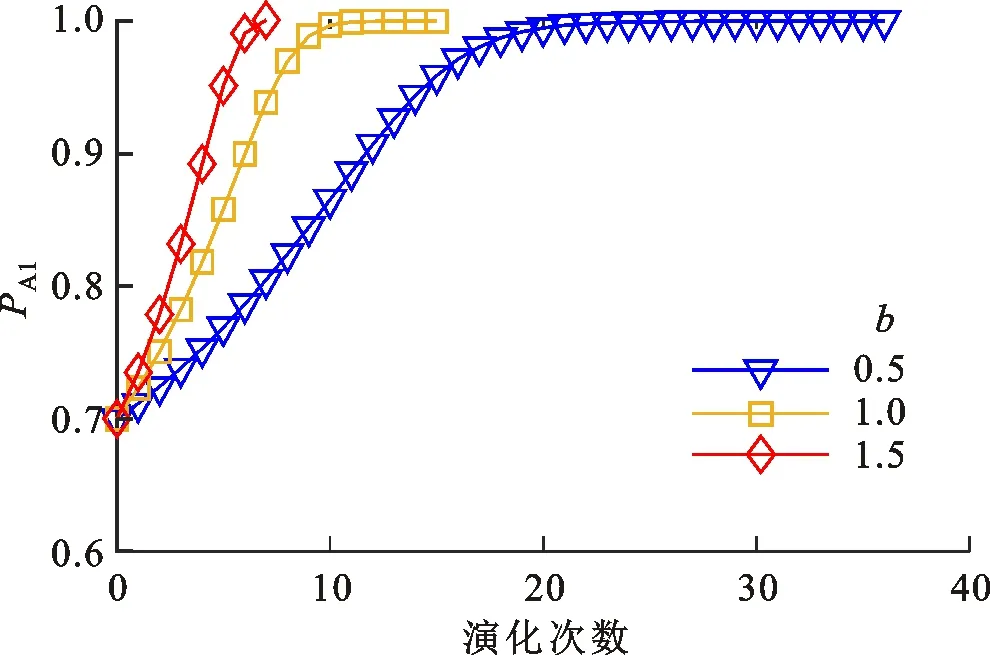
(a)攻击策略选取概率

(b)防御策略选取概率图5 不同b取值下攻防双方策略选取概率变化趋势Fig.5 Changing trend of strategy selection probability of attack and defense for different b values

分析图5可知:当b=0.5,1,1.5时,PA1达到演化稳定所需的演化次数分别为36、15、7次;PD1达到演化稳定所需的演化次数分别为117、59、39次。以b=1为基准:当b=0.5时,防御方博弈群体决策趋于稳定的速率减缓了198%;当b=1.5时,防御方博弈群体决策趋于稳定的速率提升了151%。由此可见,反思能力b可以影响博弈结果的求解速度。现实意义在于,反思能力较弱的子群体(b<1)需要更多时间适应环境才能做出决策;反思能力较强的子群体(b>1)对环境适应性较强,决策反应较快。理论上合理调整参数b,使其对应每次博弈的时间窗口,可提升博弈结果的时敏性。