多尺度低秩图像盲去模糊方法
2021-09-10周志豪张玉龙唐启凡闫金涛
周志豪,张玉龙,唐启凡,闫金涛
(西安交通大学软件学院,710049,西安)
近年来,作为图像处理领域的基本问题之一,单幅图像去模糊由于其广泛的应用而受到了关注,并通过一些里程碑式的解决方案取得了巨大的成功[1]。根据成像原理不同,图像模糊可分为散焦模糊与运动模糊,图像的散焦模糊主要是由于成像设备对焦不准而形成,运动模糊形成的主要原因是成像设备在曝光时间内抖动或者被拍摄目标在运动。单幅图像的运动模糊过程可以建模为一个清晰图像和一个模糊核的卷积,表达式为
v=u⊗h+ε
(1)
式中:u表示潜在图像;h表示运动模糊核;ε表示图像噪声;v表示已知的模糊图像;⊗是卷积操作。
图像去模糊方法可以大致分为非盲去模糊和盲去模糊两类。若模糊核已知,则研究的图像去模糊问题为非盲去模糊问题,其目标是根据给定的模糊图像和已知的模糊核估计出潜在图像。比较经典的非盲去模糊方法是基于维纳滤波[2]的方法,但是该方法对加性噪声特别敏感,恢复出的图像效果往往不佳。Richardson-Lucy方法利用了EM方法和极大似然法[3],在一定的迭代次数内图像纹理细节会随着迭代次数增加而变得清晰,但是加性噪声和振铃效应会更加明显,且迭代次数过多会导致恢复质量下降;Zhuang等提出了基于子空间数据保真度的非盲去模糊方法,以实现对不同图像内容的差分处理,取得了不错的效果[4]。
若模糊核未知则为非盲去模糊,需要从给定的模糊图像中估计出未知的模糊核与潜在图像。由于许多对不同的h与对应的u能够生成同一个v,因此图像盲去模糊问题是一个高度病态的问题。通常引入模糊图像中的先验信息作为正则项来约束方程的解空间,以此建立模型求解。Michaeli等发现不同尺度上的图像其模糊程度会改变,于是使用图像块的自相似性作为图像先验来估计模糊核[5];Xu等提出L0约束下的图像先验,能有效去除图像不必要的边缘信息,且该方法在迭代过程中不需要额外的滤波操作,从而加快了收敛速度和总运行时间[6];Lai等使用归一化的颜色线先验,在不改变边缘结构或增强噪声的情况下恢复锐利边缘,能够更好地选择图像有效的边缘[7]。
最近的一些研究工作在图像盲去模糊方面带来了很大的改进。Liu等发现具有不利结构的中间潜像的表面图通常具有较大的表面积,由此提出了从表面几何角度出发的表面感知先验,减少中间潜像表面的面积以减少那些不利的结构,使得中间潜像具有更清晰的锐边和更少的网格伪影,能更好地处理具有大饱和区域和脉冲噪声的低照度模糊图像[8];Pan等发现模糊图像中大多数图像块的最小像素值不为0,并且模糊图像的暗通道图像要比清晰图像亮,以此作为暗通道先验[9]。然而,当图像以较为明亮的像素为主时,使用暗通道先验进行模糊核估计的效果并不好。为了解决这个问题,Yan等提出了亮通道先验,并且证明了其有效性,然后将暗通道先验与亮通道先验结合为极先验带入到去模糊模型中,在处理较亮的图像时尤为有效[10]。Wen等将暗通道先验的逐像素最小化操作改为逐块最小化操作,提出了逐块局部最大梯度先验,该方法在去模糊质量、计算代价方面均好于暗通道先验方法[11]。近年来的相关工作发现,对图像梯度施加低秩先验约束,能够保留强边缘并消除潜在图像中不重要的纹理和边缘,同时还能抑制噪声对去模糊过程的影响,从而增加去模糊方法的鲁棒性[12-14]。
本文提出了一种多尺度低秩图像盲去模糊方法PLMG-Sp。结合逐块局部最大梯度先验、低秩先验为联合先验,并分别采用L0范数和加权Schatte-1/2范数进行约束,将其带入到经典的最大后验概率(MAP)框架中。在多尺度框架下,对图像进行多次降采样以消除噪声的影响。在单尺度层面,对图像施加图像填充和图像平滑方法,使用交替方向乘子法和半二次分裂法对改进的去模糊模型进行优化。在计算过程中,由于直接求解低秩正则化项的计算代价很大,将其转化为独立的r个非凸权重L1/2范数子问题,采用广义软阈值(GST)方法进行求解。最后,由估计出的模糊核与模糊图像进行非盲反卷积恢复出清晰图像。通过将本文方法与相关的最新方法在3个经典的合成数据集和两个自然模糊的数据集上进行实验,证明了本文方法的优越性。
1 相关工作
1.1 局部最大梯度先验

1.2 低秩正则化先验
近年来,基于图像非局部自相似性的低秩先验方法在图像盲去模糊领域得到广泛的应用,取得了不错的效果。优化求解低秩先验模型的一个经典方法是核范数最小化(NNM)。在此基础上,Gu等提出了加权核范数最小化(WNNM)方法,设置了一个权重向量对不同大小的奇异值进行约束,从而使NNM方法更为鲁棒[16]。相关研究表明,基于Schatte-p范数的模型比NNM更加逼近低秩模型。受WNNM启发,Xie等提出加权Schatte-p范数最小化方法,能更有效地去除噪声,从而获得更精确的结果[17]。图像u的加权Schatte-p范数定义为
(2)
式中:wi表示权重向量;σi(u)表示图像矩阵u的第i大的特征值;r表示u的行数;0 本小节将介绍所提出的逐块局部最大梯度(PLMG)先验,并通过数学推导验证其在去模糊过程中的有效性。之后,将PLMG先验以及加权Schatte-1/2范数约束的图像低秩先验作为联合图像先验带入到MAP框架中。经典的MAP框架可表达为 (3) 式中:第1项为数据保真项;第2项φ(u)和第3项ψ(h)分别为图像u和模糊核h的正则项;ξ和τ分别为φ(u)和ψ(h)的权重参数,且都大于0。 (4) 式中:i=1,2,…,k;x和y代表图像中像素点的位置;Ωi代表图像块集合中以x像素点为中心的第i个图像块;uc表示图像u的c颜色通道。本文观察到,清晰图像块的逐块局部最大梯度会随着模糊过程而变小,如图1所示。 图1 模糊图像和清晰图像的逐块局部最大梯度Fig.1 Patch-wise local maximum gradient image of blurred image and sharp image 为了验证PLMG先验在图像去模糊过程中的有效性,进行推导 (5) 由于图像先验需要‖φ(u)‖p≤‖φ(v)‖p代入到传统去模糊框架中才能有效,本文进一步转化PLMG先验。对图像进行灰度化处理,并转化为双精度类型,于是图像的像素值区间由[0,255]转变为[0,1],图像水平或垂直方向的梯度绝对值也在区间[0,1]内。采取直接相加的方式计算水平和垂直方向的图像梯度绝对值,因此图像梯度绝对值最大为2,PLMG先验转化为 2-fPLMG(u)≤2-fPLMG(v) (6) 将2-fPLMG(u)作为正则项,并施加L0范数约束,即可作为一个有效的图像先验知识带入到传统MAP图像盲去模糊框架中。 可 (7) 将所提出的联合图像先验φ(u)融入到传统的MAP框架中,得到目标函数 fPLMG(u)‖0+τ‖h‖2) (8) (9) (10) (11) 式中:α、β和γ是大于0的权重参数,当它们趋于无穷大时,式(11)的解接近于式(9)的解;Th是模糊核h的Toeplitz矩阵。式(11)可以用交替方向乘子法分别更新u、l、g和q的方式求解。当固定l、g和q时,u的求解方式为 (12) 由于矩阵P尺寸过大,引入辅助变量d,将式(12)转换为 (13) 同样地,对于式(13)也可以采用交替方向乘子法进行求解。潜在图像u的最终解为 (14) 固定u,式(13)中d的求解方式为 (15) 式(15)通过二范数求导,令等式为0,得到 2αPT(2-Pd-l)+2ζ(u-d)=0 (16) 得到 (17) 当u固定时,式(11)中l、g和q的求解方式为 (18a) (18b) (18c) 式(18)中的前两个式子都是element-wise的极小化问题,求得l和g的解为 (19) (20) 对于q的求解,首先定义权重向量w为 (21) (22) 式中δi为u的第i个奇异值。采用广义软阈值[19]方法求解式(22) (23) 式中:U和V是u的SVD分解正交矩阵;u=UΣuVT;Σu是奇异值对角矩阵。算法1给出了求解式(9)的主要过程。 算法1估计潜在图像u 输入:模糊图像v和初始模糊核h 1u←v,h←h0,α←2λ 2 repeat 3 计算逐块局部最大梯度算子P; 4 利用式(19)求解l; 5β←2η; 6 repeat 7 利用式(20)求解g; 8 利用式(23)求解q; 9γ←2μ; 10 repeat 11 利用式(17)求解d; 12 利用式(14)求解u; 13 updateγ←2γ; 14 untilγ>γmax; 15 updateβ←2β; 16 untilβ>βmax; 17 updateα←2α; 18untilα>αmax; 输出:中间潜在图像u 固定了u之后,根据文献[6]的方法,使用梯度信息而不是像素值能得到更精确的模糊核,并且在计算方面开销更小。因此,利用图像梯度来进行模糊核估计 (24) 在代码的执行过程中,为方便计算,若输入的模糊图像u为彩色图像,则将图像进行灰度化处理,之后直接进行逐块局部最大操作。在估计出最终的模糊核之后,由于最后一次单尺度去模糊得到的潜在图像缺少一定的细节,因此需要利用最后一次单尺度去模糊得到的模糊核与初始模糊图像进行非盲去模糊得到最终的清晰图像。本文使用了Zhang等的方法[20],将超拉普拉斯先验与增广拉格朗日总变差-L2方法结合起来,既能在恢复图像的过程中保留大量纹理细节,又能去除振铃伪影,使复原出的图像效果更好。 本文采用的多尺度去模糊方法框架如图2所示。首先要先初始化,若输入图像是彩色图像,则将其进行灰度化和归一化,便于后面的计算。之后进行降采样操作,根据模糊核尺寸计算出降采样次数,逐层构建图像金字塔。图像金字塔有7层,由灰度化的模糊图像开始,降采样6次分别生成{u1,u2,…,u7},其中u7是初始的灰度图像。从u1也就是最小一级的降采样图像开始,与初始化的模糊核h1进行单尺度盲去模糊得到粗糙的模糊核,再对该模糊核进行归一化与上采样操作得出下一个单尺度盲去模糊中使用的模糊核h2。在执行第7次单尺度方法之后,得出的模糊核即为最终估计出的模糊核,然后与初始模糊图像进行本文采用的非盲去模糊方法得到清晰图像。 图2 多尺度去模糊方法框架Fig.2 Framework of multi-scale deblurring method 在Köhler等[21]、Levin等[22]、Lai等[23]的共3个合成数据集以及Lai等[7]、Pan等[9]的共2个自然模糊数据集上进行了实验,并与7种近年效果优秀的图像盲去模糊方法进行了比较。由于实验数量较大,本文只给出部分实验结果进行直观比较。采用峰值信噪比rsn,p、结构相似性ssim以及累计错误率rce共3种指标来进行去模糊结果和模糊核估计的客观质量评价。 本文方法主要有5个参数λ、μ、γ、τ、αmax。其中,λ=μ=η=4×10-3,τ=2,αmax=106。图像金字塔的层数,即降采样的次数,根据预设的模糊核尺寸进行计算。在单尺度层面,由于需要兼顾方法的精度与速度,本文对单尺度中u和h的交替迭代次数设置为5。 为了选取计算逐块局部最大梯度算子的图像块尺寸,在Köhler等数据集[21]上对5×5、15×15、25×25、35×35像素共4个图像块尺寸进行了实验,结果表明,在该数据集上所有结果的rsn,p平均值分别为29.25、30.07、29.73、29.58。因此,最终选取图像块尺寸为15×15像素。 Levin等数据集[22]包含4幅地真图像与8个不同的模糊核,以及生成的32幅模糊图像。该数据集通过锁定三脚架的Z轴旋转手柄,并同时松开X轴和Y轴手柄,捕获均匀模糊的模糊图像。本文将估计得到的模糊核去模糊误差与真实模糊核去模糊误差计算比值得到错误率。对于每幅清晰图像,错误率越低代表恢复性能越好;对于每个错误率,成功率越高越好。在Levin等数据集[22]上进行实验,并与Pan等[9]、Yan等[10]、Chen等[15]、Cho等[24]、Liu等[25]、Jin等[26]的共6个方法进行了比较,结果如图3所示。可以看出,本文方法在性能上优于以往最先进的几种方法,在错误率较低的时候成功率已经在几种方法中最高,且在错误率为3时已经有100%的成功率。 图3 在Levin等数据集[22]上的错误率Fig.3 Error ratio on the dataset of Levin et al.[22] Köhler等数据集[21]包含4幅地真图像和12个模糊核,以及生成的48幅模糊图像。与以往基准数据集对各个指标进行评估的方式不同,该数据集对于每一幅地真图像,将其沿着不同的相机运动轨迹平移生成199幅不同位置的地真图像,并将不同方法对48幅模糊图像进行复原得到的清晰图像与相对应的199幅图像进行评估,选取其中的最优值作为这幅模糊图像的最终定量指标。本文采取该方式对各个方法复原的图像进行评估。在Köhler等数据集[21]上进行实验,并与Xu等[6]、Pan等[9]、Chen等[15]、Cho等[24]、Liu等[25]、Jin等[26]的共6个方法进行比较,结果如图4所示。可以看出,本文方法相对于其他方法在rsn,p和ssim上有一定提升。 (a)平均rsn,p (b)平均ssim图4 在Köhler等数据集[21]上的平均rsn,p与ssim Fig.4 Average rsn,p and ssim values on the dataset of Köhler et al.[21] Köhler等数据集[21]中的一幅模糊图像实验结果如图5所示。可以看出:本文方法性能更优,在细节纹理的恢复方面有较好的效果;本文方法估计出的模糊核与初始的模糊核更为贴近,且没有多余的白色轨迹。模糊核中白色轨迹的本质是相机的抖动轨迹,一般是连续的并且没有多余的白色瑕疵。 (a)原始模糊图像, (b)Cho等[24]的结果, (c)Xu等[26]的结果, (d)Pan等[9]的结果, rsn,p=27.96 dB rsn,p=31.31 dB rsn,p=31.14 dB rsn,p=32.02 dB (e)Jin等[6]的结果, (f)Liu等[9]的结果, (g)Chen等[15]的结果, (h)本文结果, rsn,p=31.79 dB rsn,p=31.95 dB rsn,p=32.17 dB rsn,p=32.35 dB图5 在Köhler等数据集[21]上的实验结果Fig.5 Experimental results on the dataset of Köhler et al.[21] 在Lai等[7]、Pan等[9]的两个自然数据集进行实验,并与Pan等[9]、Chen等[15]、Liu等[25]的这3个最先进的方法进行比较。选取有代表性Woman和Fountain图像进行去模糊效果展示,Woman和Fountain图像分别选自Pan等[9]和Lai等数据集[7],结果如图6所示。可以看出:本文方法恢复出的清晰图像效果较好,有较少的振铃效应并保留了大多数细节,具有比较高的稳定性;本文方法估计出的模糊核更为精确,没有多余的白色轨迹。 图6 Woman和Fountain图像的去模糊结果Fig.6 Deblurring results of Woman and Fountain images 3.4.1 低秩优势 Lai等数据集[23]通过随机采样的6D相机轨迹生成均匀模糊核,然后使用具有1%高斯噪声的卷积模型来合成均匀模糊图像。在该数据集上进行实验,并与Pan等[9]、Chen等[15]、Liu等[25]、PLMG方法、本文PLMG-Sp方法进行比较,部分结果如图7所示。可以看出,PLMG-Sp方法对于潜在图像的纹理恢复更好,得到的模糊核没有出现斑驳的白色轨迹,说明本文方法估计出的模糊核更加精确。这是由于使用了低秩先验可以保留图像中的强边缘信息并能够减少噪声信息对图像去模糊过程中的不利影响[14],以达到更好的去模糊效果。表1是各方法处理图7图像得到的rsn,p与ssim,可以看出,本文方法拥有更出色的去模糊效果。 图7 验证低秩正则化项有效性的实验结果Fig.7 Experimental results verifying effectiveness of low-rank regularization terms 表1 在Lai等数据集[23]上的rsn,p和ssim 3.4.2 运行时间 各方法在图6两幅图像上的运行时间如表2所示。可以看出:PLMG方法在时间上相比Pan等[9]、Chen等[15]、Liu等[25]的方法有明显优势,但是去模糊性能方面并未有提升;加入了低秩正则化项后的PLMG-Sp方法运行时间相比Pan等[9]、Yan等[10]、Liu等[25]的方法的有一定减少,同时仍能保持不错的去模糊效果;Cho等[24]的方法所公布的代码是用C语言编写,而其他方法都是用MATLAB编写,因此该方法时间较短,但去模糊效果不佳。 表2 各方法的运行时间对比 (1)本文提出了一种基于逐块局部最大梯度先验和低秩先验的多尺度图像盲去模糊方法。从直观和理论两个方面分析了PLMG先验的正确性,并对其施加L0范数约束作为正则化项。将PLMG拆分为3个简单的算子以替代复杂的直接求局部梯度块最大值的过程。将PLMG先验与低秩先验作为联合先验融入到MAP去模糊框架中进行计算。 (2)本文利用了高效的交替方向乘子法以及半二次方分裂法,使得公式分裂出的子公式都能得到闭合解。由于对Schatte-1/2范数约束的低秩正则化项直接求解计算量很大,本文将其转化为r个独立的非凸权重子问题,然后使用广义软阈值方法进行求解。 (3)本文在3个合成数据集以及2个真实数据集上进行了实验,实验结果表明,本文方法在保证一定运算时间的情况下,可以更准确地估计模糊核,且能够有效抑制潜在图像的振铃效应并保留大多细节,使得恢复的图像具有更好的表现。2 基于逐块局部最大梯度和低秩的图像盲去模糊方法
2.1 联合图像先验去模糊模型

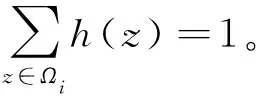
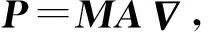
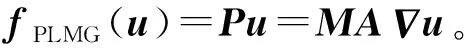
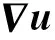
2.2 潜在图像u估计
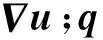
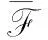

2.3 模糊核h估计
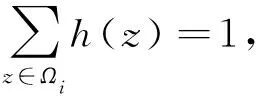
2.4 本文方法

3 实验结果及分析
3.1 参数设置
3.2 合成数据集实验结果
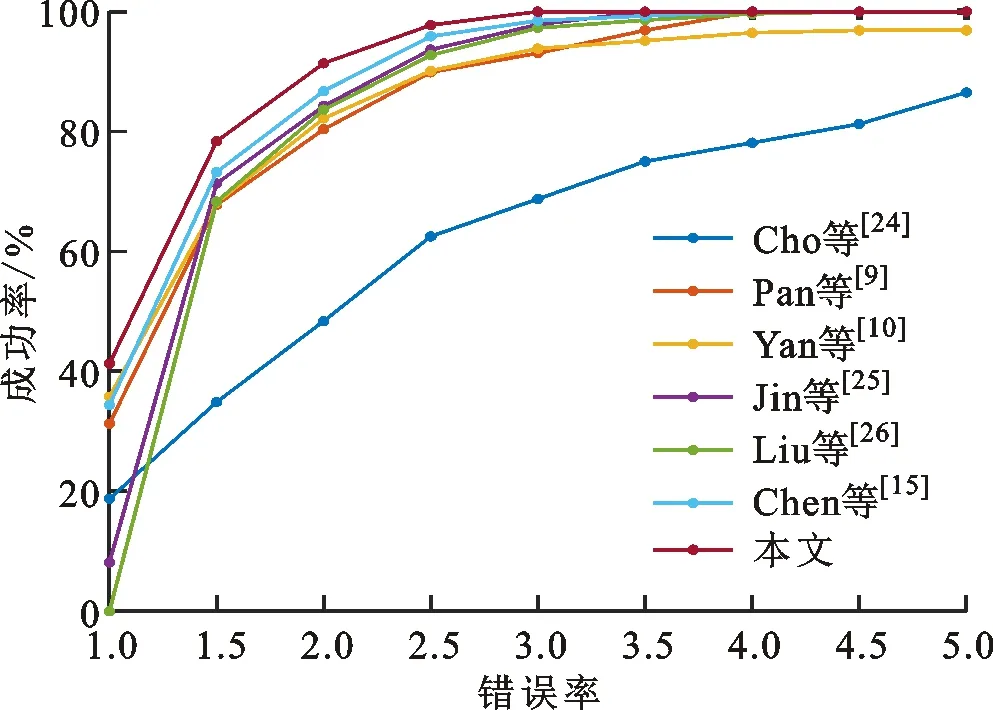
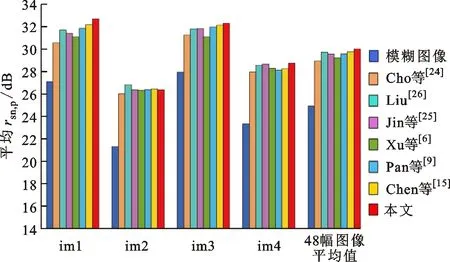
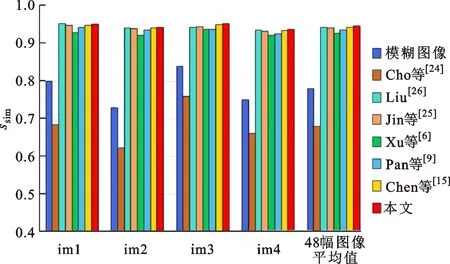


3.3 自然数据集实验结果

3.4 方法分析



4 结 论
