矩形双通道饱和沸腾传热特性试验研究
2021-09-10霍福强王腾严天宇毕勤成
霍福强,王腾,严天宇,毕勤成
(西安交通大学能源与动力工程学院,710049,西安)
符号表
A/m2流通截面积
Ah/m2有效加热横截面积
a/m 通道宽边长
B沸腾数
b/m 通道窄边长
Cpl/(kJ·(kg·℃)-1) 比热容
De/m 当量直径
E对流换热增强因子
F对流换热因子修正值
Hb/(kJ·kg-1) 主流体焓
Hs/(kJ·kg-1) 饱和焓
Hin/(kJ·kg-1) 入口焓
Hfg/(kJ·kg-1) 汽化潜热
htp/(kW·(m2·℃)-1) 两相传热系数
hsp/(kW·(m2·℃)-1) 单相传热系数
hnb/(kW·(m2·℃)-1) 泡核沸腾传热系数
hcb/(kW·(m2·℃)-1) 对流沸腾传热系数
L/m 试验段有效长度
M测量物理量
Mw工质相对分子质量
EME平均误差
EMAE平均绝对误差
N测量物理量
P/kW 加热功率
pR系统压力与临界压力之比
PF/m 润湿周长
PH/m 加热周长
Prl液相普朗特数
Q/kW 流体吸热量
q/(kW·m-2) 热流密度
Rel液相雷诺数
S泡核沸腾抑制因子
s标准偏差
TWI/℃ 内壁温
TWO/℃ 外壁温
Tf/℃ 流体温度
Wefo全液相韦伯数
xeq热力学干度
XttMartinelli参数
z/m 距入口截面距离
ΔTsat/℃ 壁面过热度
ΔPsat/Pa 壁面过热度对应饱和压差
η/% 热效率
φ/(kW·m-3) 体积释热率
δ/m 加热板壁厚
λl/(w·(m·℃)-1) 液相导热系数
ρl/(kg·m-3) 液相密度
ρg/(kg·m-3) 气相密度
σ/(N·m-1) 表面张力
σi平均相对误差
随着大规模集成电路、航天器和核电等先进技术的迅速发展,人们对大功率、结构紧凑型换热器需求愈发强烈[1]。矩形窄通道凭借结构简单、紧凑且可强化传热等优势倍受关注[2-3]。在核电反应堆中,板式燃料的应用便是典型的例子[4]。为了高效可靠地利用此类型通道,需要对矩形窄通道内流动传热特性及传热机理有一个深入的认识。到目前为止,已有大量学者对窄矩形通道内的流动传热特性进行了研究。
Gong等研究了低质量流速条件下矩形通道内沸腾换热特性,结果发现质量流速和干度对矩形通道内流体换热影响微弱,这表明传热过程中核态沸腾起主导作用[5]。Shiferaw等学者在干度大于0.2时也发现了同样的现象[6-9]。郑银银通过数值模拟的方法研究矩形通道内饱和沸腾及压降特性发现,增大质量流速和干度,沸腾换热系数增大,而传热系数的变化受热流密度的影响几乎可以忽略[10],这与Li等学者得出的结论[11-14]一致。
通过上述研究发现,学者们对于窄矩形通道内的传热特性及换热机理的认识,并未得出一致的看法。此外,尽管已有学者对矩形通道内热工水力特性进行了大量研究,但绝大部分学者多以制冷剂或者空气水混合物为工质,且多集中于对矩形单通道的研究,而在实际换热设备中多以并联管路形式存在。并联管路内的流量分配会直接影响换热设备表面温度及换热效率甚至可能会引起局部过热等问题,这使得并联通道内流动沸腾换热过程更加复杂,因此对并联窄矩形通道内沸腾换热特性的研究显得十分有意义。本文将围绕并联窄矩形通道内饱和沸腾换热及流量分配特性展开,并基于试验结果分析沸腾换热影响因素,比较双通道间换热特性异同,最后与现存传热关联式对比并提出改进后关联式。
1 试验系统与方法
1.1 试验系统
图1为传热特性研究试验台流程图。试验工质是硬度为0、电导率低于0.5 μs·cm-1的去离子水。水箱中的去离子水经过滤器过滤和柱塞泵升压后流入两个回路,一路经回水阀直接返回水箱,另一路进入主回路。进入主回路的去离子水经回热器、预热器后进入试验段,吸收试验段产生的热量,被沿途回热器、冷凝器冷却到一定温度后返回水箱完成循环。试验段通过通以低电压、大电流方法对矩形通道的4个壁面同时加热,测量数据由IMP3095数据采集板实时记录,采集周期为1 s。
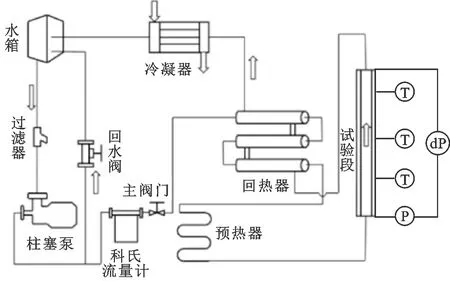
图1 传热特性研究试验台流程图Fig.1 Schematic diagram of heat transfer experiment
1.2 试验段
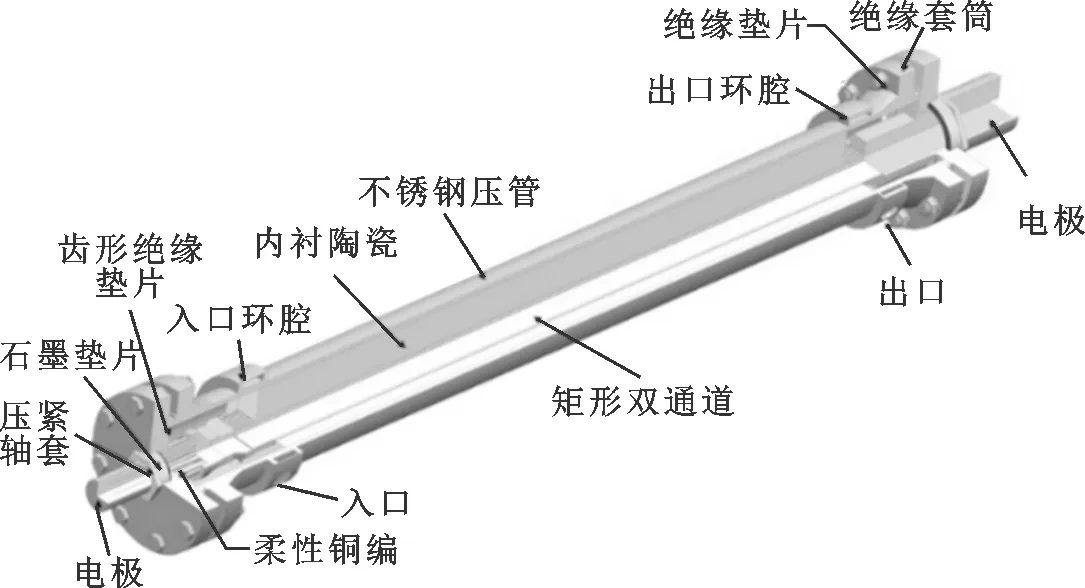
(a)试验段装配图
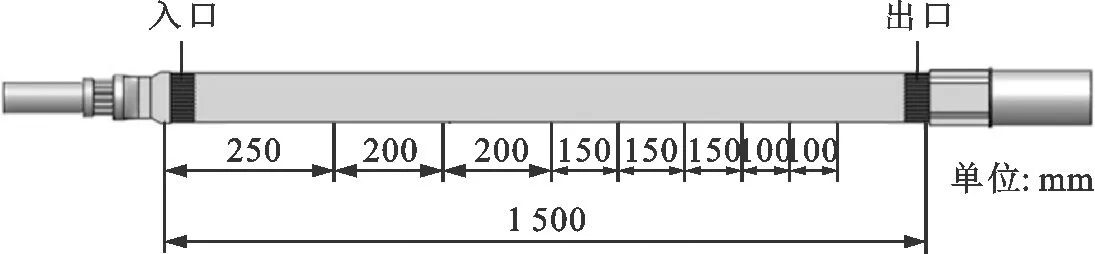
(b)测温点布置图
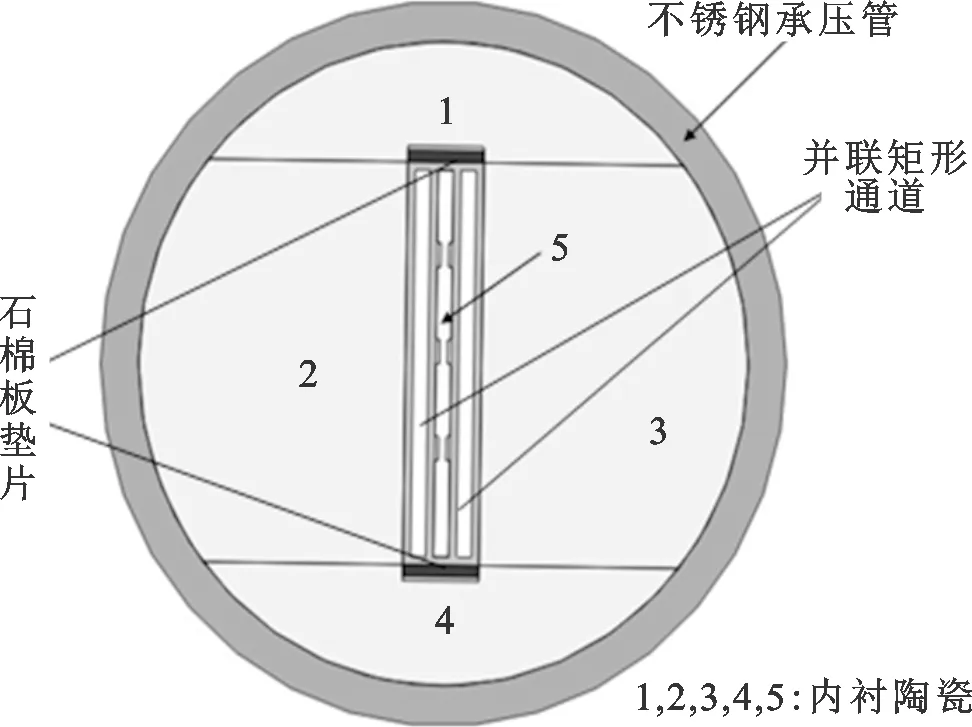
(c)试验段截面图
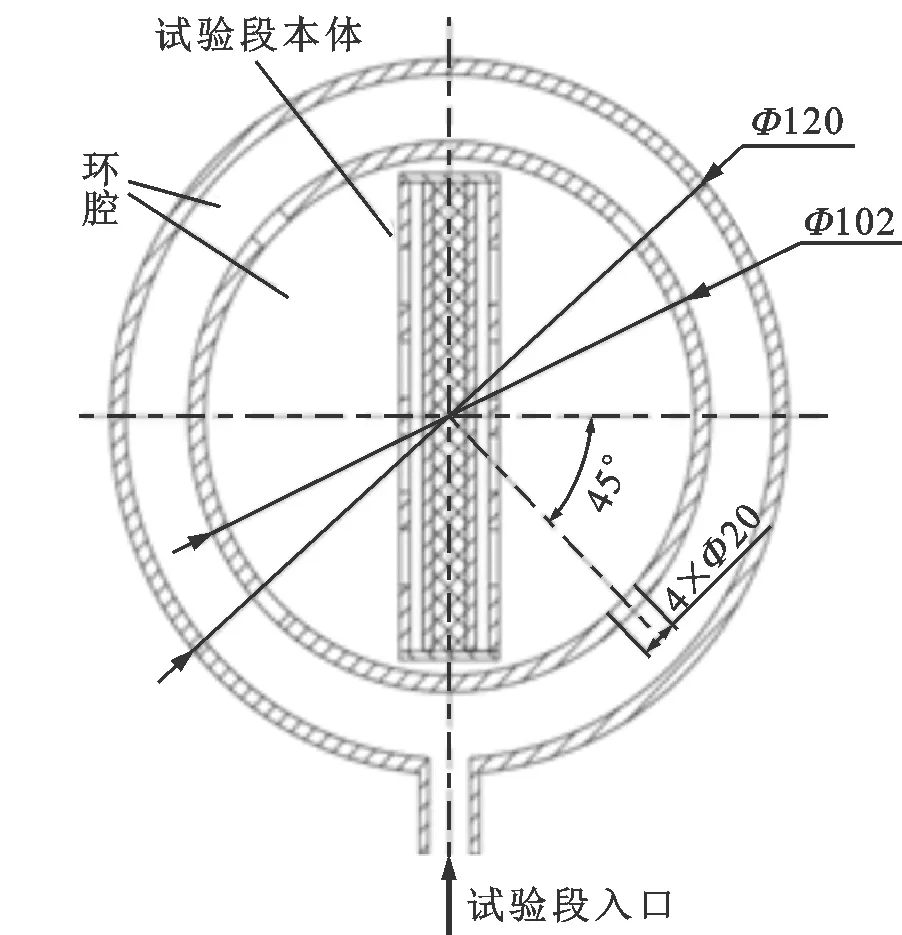
(d)试验段入口环腔结构

(e)试验段单侧入口示意图图2 试验段结构示意图Fig.2 Schematic diagram of test section
图2为试验段结构图。图2a为试验段装配图,包括试验段本体和辅助结构两大部分。图2b表明了试验段本体结构及其温度测点分布。试验段本体包括进出口两侧电极、柔性铜编、并联矩形通道及其连接结构,每个矩形通道每个测温截面布置3个测温点,分别通过本体内陶瓷板测量与陶瓷板接触的两个壁面的温度。辅助结构由承压、绝缘、密封、热变形吸收及进出口5部分组成。①试验件通过氧化铝/锆陶瓷配合不锈钢管满足承压需求;②为保证试验段本体和外侧承压钢管间的绝缘,法兰之间采用耐高温石棉板垫片配合齿形垫片分隔,螺栓孔中使用石棉板制作的绝缘套筒保证不接触,螺栓和法兰间使用石棉板绝缘垫片使其绝缘;此外为保证柔性铜编不与不锈钢管接触,在铜编外使用陶瓷管实现与管壁的分隔;③试验件通过轴套压紧石墨垫片保证法兰和电极之间密封,法兰之间则使用垫片密封;④在进口部分的连接处增加了一段柔性铜编,并在内部陶瓷板中添加石棉板垫片以上述两种方式分别吸收试验段沿流动方向和宽度方向的热膨胀;⑤试验段进口采用双层环腔设计,保证了并联双通道在入口处的均匀分配。图2d、图2e分别为入口双层环腔和试验段本体单侧入口结构示意图。从图2d可以看出,试验段通过在管壁上对称开孔,使得流体可以在环室中充分混合;图2e可以看出,试验段本体通过将最外层不锈钢板进口一段距离利用线切割成栅格形状,通过增加阻力的方式保证入口两侧通道流量分配均匀。进出口内部结构均为对称布置。试验段本体外侧通过和不同形状的陶瓷组合后放于承压不锈钢管中,其截面如图2c。不锈钢管和试验段本体间通过4块不同形状陶瓷填充进行连接,陶瓷组件一方面起到了隔绝流体、承压的作用,另一方面防止试验段本体沿矩形通道窄边方向发生热膨胀,石棉板垫片用来防止不锈钢板吸热后沿矩形通道长边方向的热变形,试验段本体内陶瓷板5的作用为辅助壁温测量。试验段本体在制作完成后通过测定矩形通道体积方法对间隙进行了检测,通过计算平均间隙发现左右两通道与初期间隙设计值之间的偏差不超过2%,满足设计要求。
1.3 数据处理
矩形通道当量直径为
(1)
式中:A为矩形单通道横截面积;PF为通道润湿周长;a为矩形通道宽边长;b为矩形通道窄边长(近2 mm)。
试验段热效率为
(2)
式中:Q为单相流体吸热量;P为试验段加热功率,本试验热效率取0.9。
试验段热流密度为
(3)
式中:Ah双矩形通道加热面积。
试验段内壁面温度为
(4)
式中:TWO为外壁面温度;φ为体积释热率;λ为不锈钢导热系数;δ为加热板厚度;外壁温由测温截面处3个测点平均值计算。
计算截面处流体平均焓为
(5)
式中:Hin为试验段入口流体平均焓;z为计算截面据入口距离;L为矩形通道总长度。
热力学平均干度为
(6)
式中:Hs为对应压力下流体饱和状态焓;Hfg为对应压力下流体汽化潜热。
沸腾传热系数为
(7)
式中:Tf为计算截面处流体平均温度。
为保证数据处理过程准确性,计算所需工质物性参数采用NIST9.1软件中数据。
1.4 不确定度分析
通过仪表测量以及计算得到的物理量和真实值之间存在一定的偏差,该偏差由不确定度表示。一般情况下测量的物理量包括直接测量物理量和间接测量物理量。
直接测量物理量M不确定度通过下式确定
Mi=MSC±δMi
(8)
式中:Mi为物理量测量平均值;MSC为单次测量值;δMi为不确定度。
假设间接测量物理量N由若干个直接测量量X组成,不确定度可表示为
(9)
式中;n为直接测量量个数;δxi为直接测量量不确定度。
表1给出了试验所用测量仪表量程及测量精度。
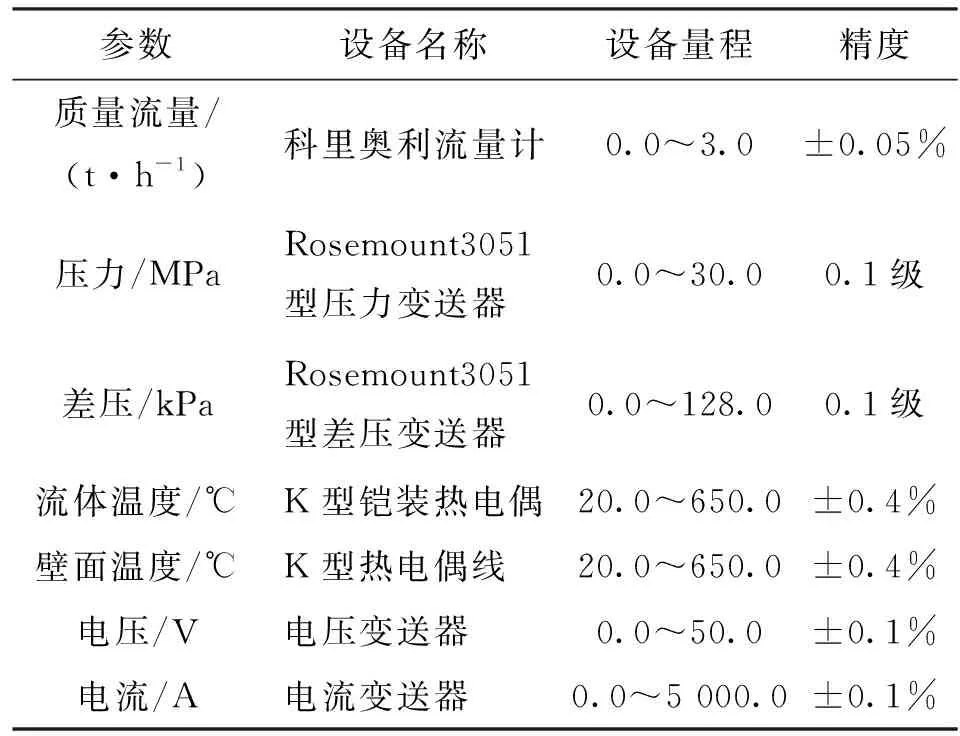
表1 测量参数与仪表关键参数
试验所得测量值不确定度分析结果见表2。
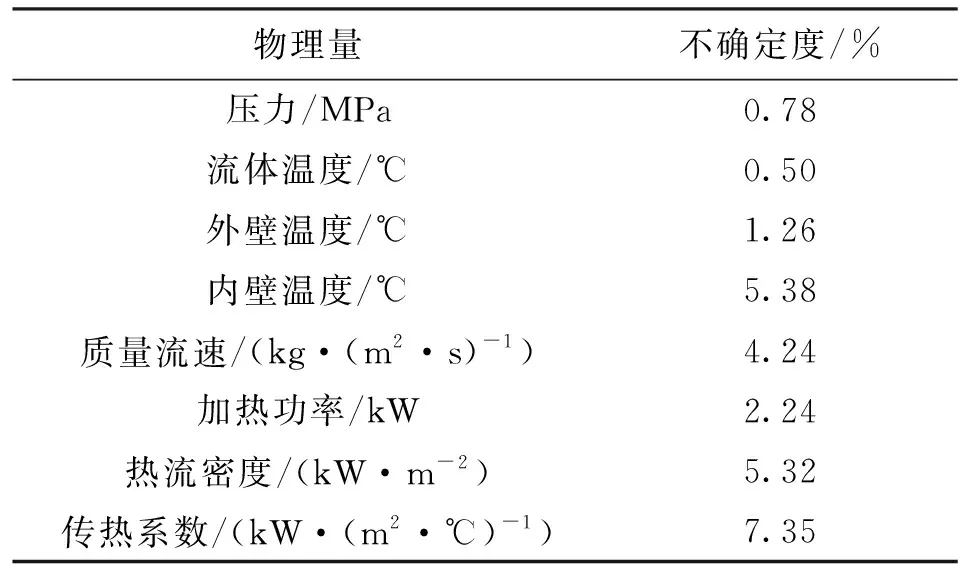
表2 测量值不确定度汇总表
2 试验结果与讨论
2.1 系统标定
正式试验前,需对试验回路进行标定,以验证系统精度与可靠性。通过竖直矩形通道单相流动传热试验完成系统标定,标定参数:压力为2.1~10 MPa,质量流速为1 000~1 500 kg/(m2·s)。将试验所得Nu值与DB公式预测结果进行对比,结果如图3。由图3可以看出,试验所得Nu值与DB公式预测值存在偏差,预测值普遍低于试验值,Ghione等研究窄矩形通道内水换热特性时也得到相似的结论。标定结果表明系统精度满足试验需求,相关测量仪器及数据处理方法可靠[15-17]。
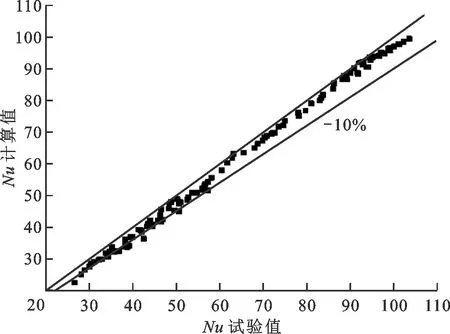
图3 传热系统标定结果Fig.3 Calibration results of heat transfer system
2.2 典型传热结果
图4为窄矩形通道内流体传热特性随焓的变化曲线,图中试验参数范围为入口压力2.1 MPa、质量流速1 000 kg/(m2·s)、热流密度200 kW/m2及入口过冷度12~45 ℃。图4a为试验段内壁面温度随焓的变化曲线,图4b为传热系数随焓的变化。图4a表明,过冷水进入试验段后,壁面温度沿流动方向近似线性增加。当增长至产生气泡所需过热度时,过冷沸腾发生,壁面温度增加趋势减缓,至饱和沸腾后,壁面温度趋于定值,在略高于饱和温度的附近小幅波动。
图4b为流体分别经历单相、过冷沸腾和饱和沸腾3种状态时传热系数变化特点。在单相区,传热系数随着壁温升高缓慢增长,当壁温升高到一定过热度后在壁面汽化核心处产生气泡,此时流体吸收的热量一部分用于增加显热,另一部分使自身相变,流体并未达到饱和温度,此阶段为过冷沸腾段。过冷沸腾段产生的气泡很快在主流中被冷凝,气泡并未成长和脱离,但是气泡的产生增加了热边界层内扰动,传热阻力减小,换热系数急剧增加,壁温增长速度开始变慢。流体温度增加至当地饱和温度时,进入饱和沸腾阶段。饱和沸腾后,受阻力影响壁面温度略有下降,流体的传热系数在焓低于1 016 kJ/kg时基本趋于稳定。焓处于1 016~1 090 kJ/kg之间时,传热系数出现一定幅度的增加。原因可能是随着流体吸热量增加,通道内气泡产生速率增加,产生的气泡之间发生合并,大气泡周围的液体在气泡和重力影响作用下形成回流,使得回流的液体和上升液体间发生剧烈扰动,从而形成强烈的漩涡,尖角区的存在也使得流体发生区别于圆管内的二次回流,因此传热特性得到了一定程度的强化。具体高参数工况下窄矩形通道内两相流动特性还需进行更加深入的研究。
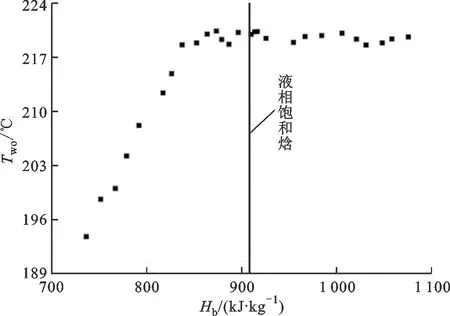
(a)壁温随焓的变化
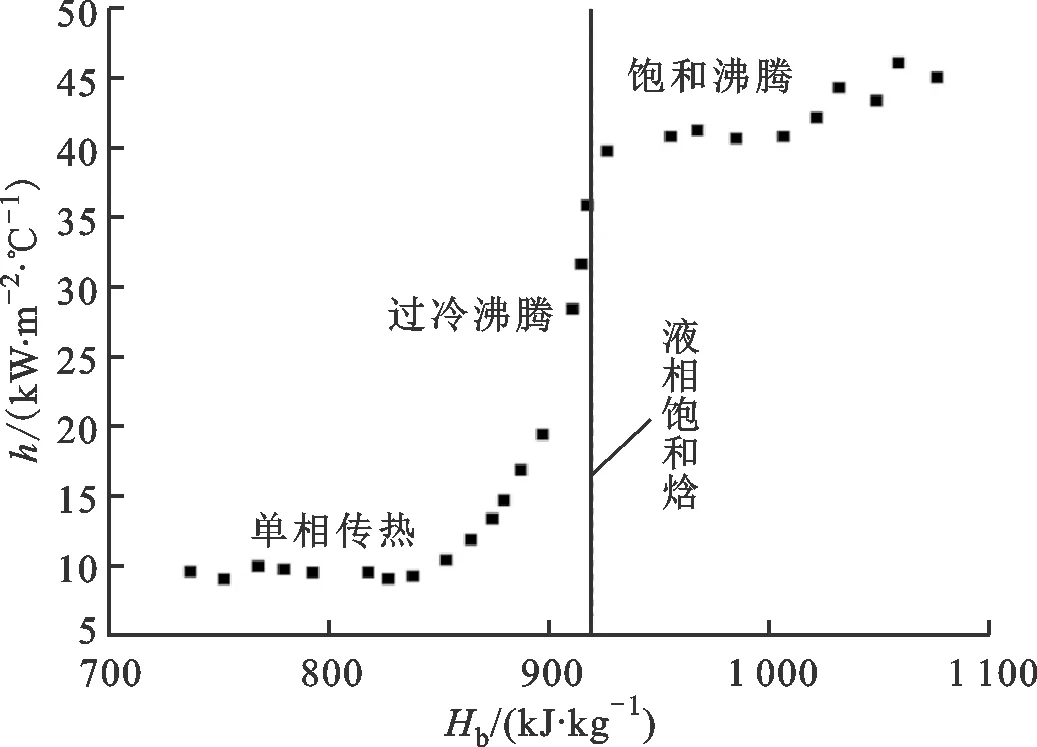
(b)传热系数随焓的变化图4 壁温与传热系数随焓的变化Fig.4 Wall temperature and heat transfer coefficient versus enthalpy
图5反映了流体传热系数随壁面过热度的变化规律,图中工况参数包括入口压力2.1 MPa、质量流速1 000 kg/(m2·s)、热流密度200 kW/m2。从图5可以看出,流体以一定过冷度进入试验段,随着壁面温度增加,传热系数缓慢增加。当壁面过热度ΔTs增大到一定值后,试验段某个截面开始产生气泡,该位置称为过冷沸腾起始点,此点后由于气泡的生成使得传热特性发生显著变化,传热系数急剧增大直至饱和沸腾发生。图5中传热曲线的变化趋势也反映出当曲线发生明显转折时沸腾发生。
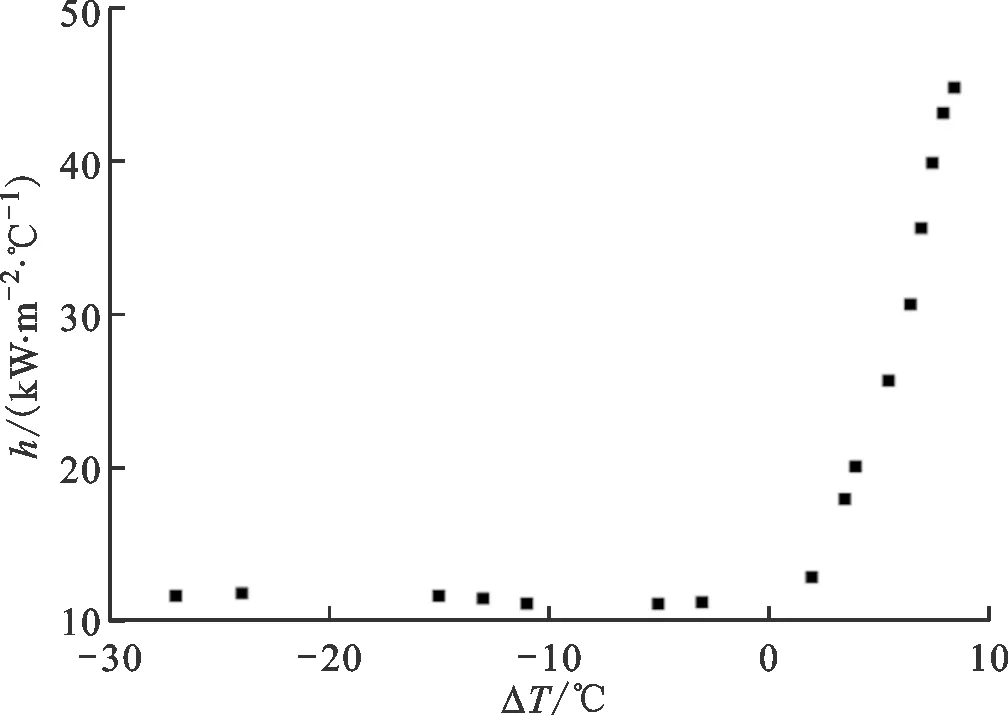
图5 壁面过热度对传热影响Fig.5 Effect of wall superheat on heat transfer
上述结果表明,矩形通道内的流体沸腾过程传热规律与常规圆形通道在一定范围内无明显差异,随着流体吸热量增加,特殊的矩形通道结构使得传热在一定程度上得到强化。总体来讲,随着流体相变的发生,使得传热特性发生大幅改善,传热壁面维持在相对均匀的温度,流体进入两相区域后,随着干度的增加其传热系数基本趋于稳定。
2.3 矩形双通道传热特性
不同于单通道,多通道中流量分配是需重点关注的特性之一。图6是质量流速为1 000 kg/(m2·s)、入口温度为182.5 ℃、热流密度分别为100 kW/m2和200 kW/m2时沿流动方向双通道内壁温变化曲线,图6中L和R分别表示并联的左右两个通道。当热流密度为100 kW/m2时,可以看到流体从入口单相到出口两相过程壁温变化趋势。流体处于单相时,内壁温沿流动方向近似线性增加,当壁温达到一定过热度时产生气泡,传热机理由单相对流换热转变为饱和沸腾传热,此时传热效果大大改善,壁温增加到一定值时基本不再变化。热流密度提高至200 kW/m2,壁温拐点提前,沸腾提前发生。当热流密度为100 kW/m2时两个矩形通道内壁温绝对差值为0.8 ℃,200 kW/m2时为0.5 ℃。
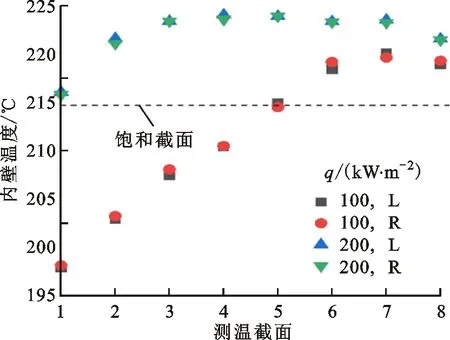
图6 双通道壁面温度的变化Fig.6 Double channel wall temperature diagram
图7给出了试验段入口压力2.1 MPa、热流密度200 kW/m2时,质量流速对两相沸腾传热影响,其中质量流速包括1 000、1 250和1 500 kg/(m2·s)。图7表明,工质进入两相区后,当热力学干度低于0.04时,传热系数缓慢上升;当干度处于0.04~0.1之间时,传热系数整体变化趋势趋于稳定,这说明饱和沸腾发生后质量流速的影响逐渐减弱。这是因为壁面上汽化核心数量增加,产生的气泡经历生成、长大和脱离过程,此过程的扰动弱化了质量流速对换热的影响,沸腾换热占主导地位;也有学者指出,两相区换热不受质量流速影响的一部分原因归于较小尺寸通道内表面张力的作用使得两相难以分离[18];从传热机理来看,在发生沸腾的热边界层中,传热特性与气泡行为有很大关系,边界层中介质大部分处于饱和状态而气泡液膜过热,所以此时也可以认为沸腾传热不受主流流动的影响。在系统其他参数确定后,传热效果并不会随着质量流速的变化而产生较大变化。通过计算发现同一质量流速下的并联通道,传热特性的变化趋势、传热强弱程度以及从过冷沸腾到饱和沸腾的转折点整体不存在较大差异。通过计算可知,右侧通道与左侧通道在相同位置、相同工况下换热系数的比值最大为1.1,最小为0.96。
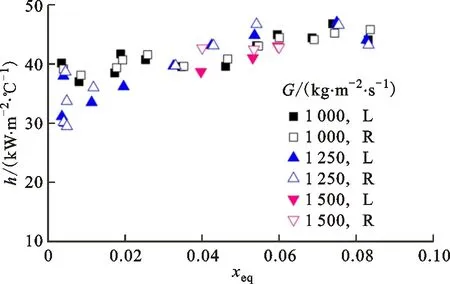
图7 质量流速对沸腾换热特性的影响Fig.7 Effect of mass flow rate on boiling heat transfer
图8为试验段入口压力2.1 MPa、质量流速1 000 kg/(m2·s)时不同热流密度下传热系数随热力学干度变化曲线,热流密度包括100、200和300 kW/m2。图8表明,工质吸热发生相变后在热力学干度相同时,随着热流密度增加,传热系数变大。这是因为随着热流密度增加,壁温升高速度变快,壁面过热度越高,气泡生成、成长和脱离频率加快,使得流体扰动更加剧烈,从而使传热得到加强。从图8中传热系数变化趋势也可以看出,热流密度越大,发生沸腾的时间越早。由于相同工况条件下左侧和右侧两个矩形通道内换热特性相差无异,可以推断出两个通道内流体分配较为均匀。
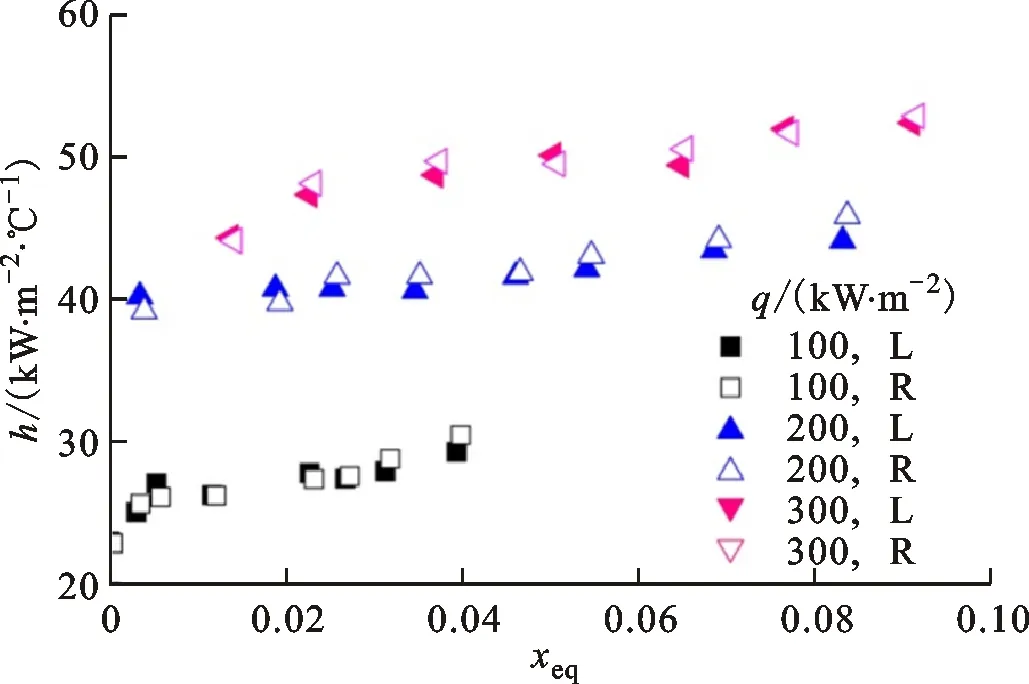
图8 热流密度对沸腾换热特性的影响Fig.8 Effect of heat flux on boiling heat transfer
图9为质量流速1 000 kg/(m2·s)、热流密度300 kW/m2时不同试验段入口压力工况下传热特性变化曲线,入口压力包括2.1、6.0和10.0 MPa。图9表明,在相同的热力学干度条件下,随着压力的增加,沸腾传热系数增大,传热特性增强,这主要归结于压力的增大使得表面张力和液相气相密度比减小,更加有利于激活汽化核心,并且随着压力的升高,沸腾所需过热度降低,从而使得传热系数增加;当压力分别为2.1和6.0 MPa时传热系数相差较小;此外图9也表明饱和沸腾后的流体在一定的干度范围内不会发生较大波动。这也再次佐证了沸腾传热过程中核态沸腾占主导地位。经计算左右两通道在相同位置、相同工况条件下传热系数之比最大为1.08,最小为0.97。
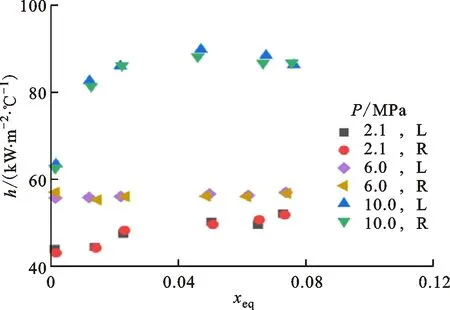
图9 压力对传热特性的影响Fig.9 Effect of pressure on boiling heat transfer
图10给出了入口压力为2.1~10 MPa、入口温度为80~299 ℃、质量流速为1 000~1 500 kg/(m2·s)、热流密度为100~300 kW/m2工况下并联双通道内换热系数对比图。图中:hR为右侧通道传热系数;hL为左侧通道传热系数。从图10可以看出,在一定的参数范围内,两个通道间的传热系数之间的偏差低于±7%,这表明两个通道间的流量分配基本均匀。
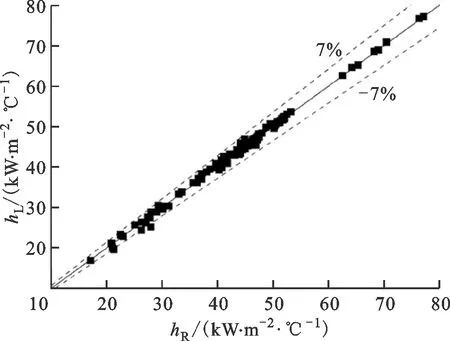
图10 双通道换热系数对比图Fig.10 Comparison of heat transfer coefficient between two channels
图6~10表明,从传热角度看,两个通道之间的壁温分布和传热系数变化有着几乎一样的趋势。传热系数的大小、传热过程的变化位置都无太大差异。通过对比相同位置、相同工况下的传热系数值,两个通道间的最大差值不超过±7%,由于在不同流量下,包括壁温、传热系数以及干度都会存在一定偏差,由此得出,并联双矩形通道间的流量分配较为均匀。
2.4 传热关联式对比
传热系数的精确预测是设计需求中最重要的一项。学者已提出众多的经验关联式和理论模型,然而考虑到两相流动的复杂性,很难在较大的参数范围内对试验走势进行精准预测。文中选取了Chen公式[19]、Liu公式[20]、Kim公式[21]、Cooper公式[22]和Shah公式[23]5个关联式与所得试验数据进行对比。以下为5种关联式表达形式:
Chen公式表达式
htp=Ehsp+Shnb
(10)
(11)
(12)
Liu公式表达式
(13)
(14)
(15)
Kim公式表达式
(16)
(17)
(18)
Cooper公式表达式
htp=55pR-0.12(-lgpR-0.55)Mw-0.5q0.67
(19)
Shah公式表达式
htp=max(E,S)hsp
(20)
(21)
E=230B0.5exp(2.74N-0.1),B>3×10-5
(22)
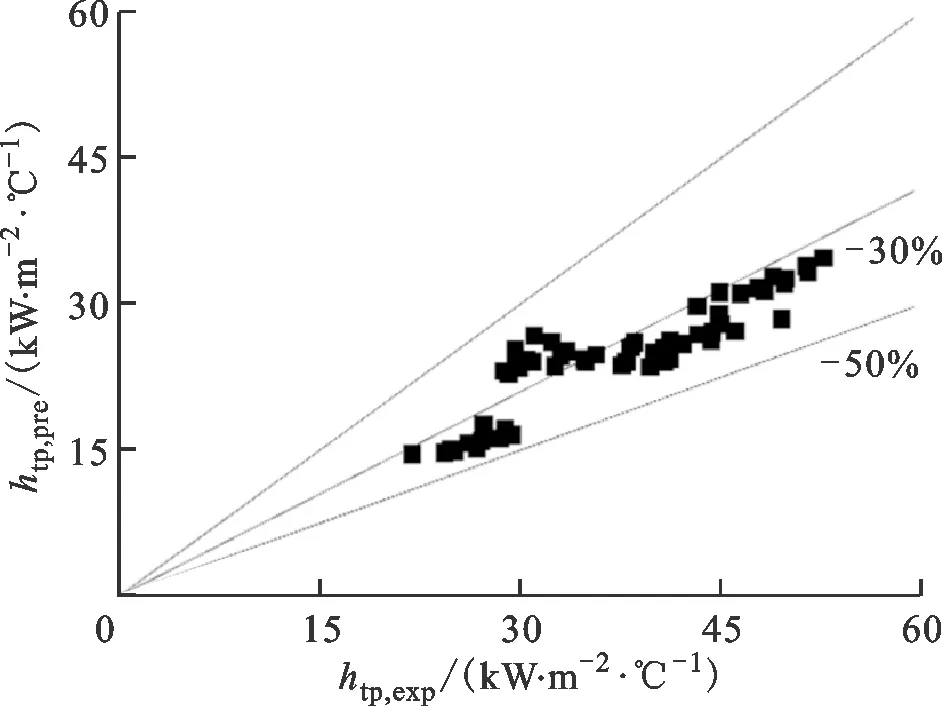
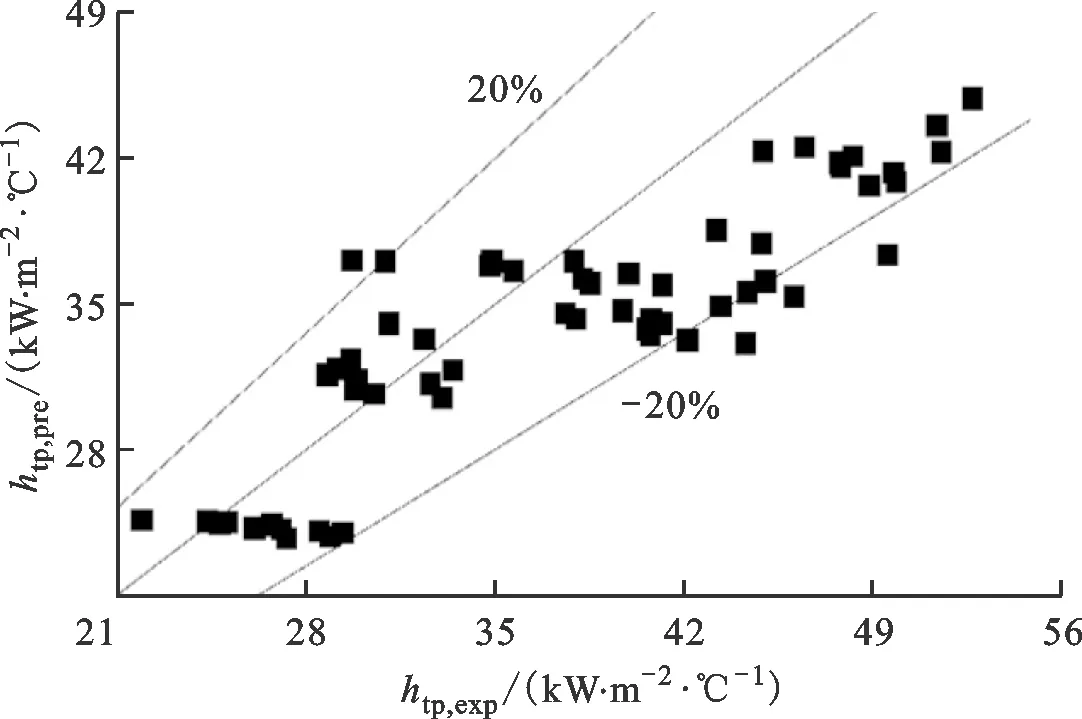
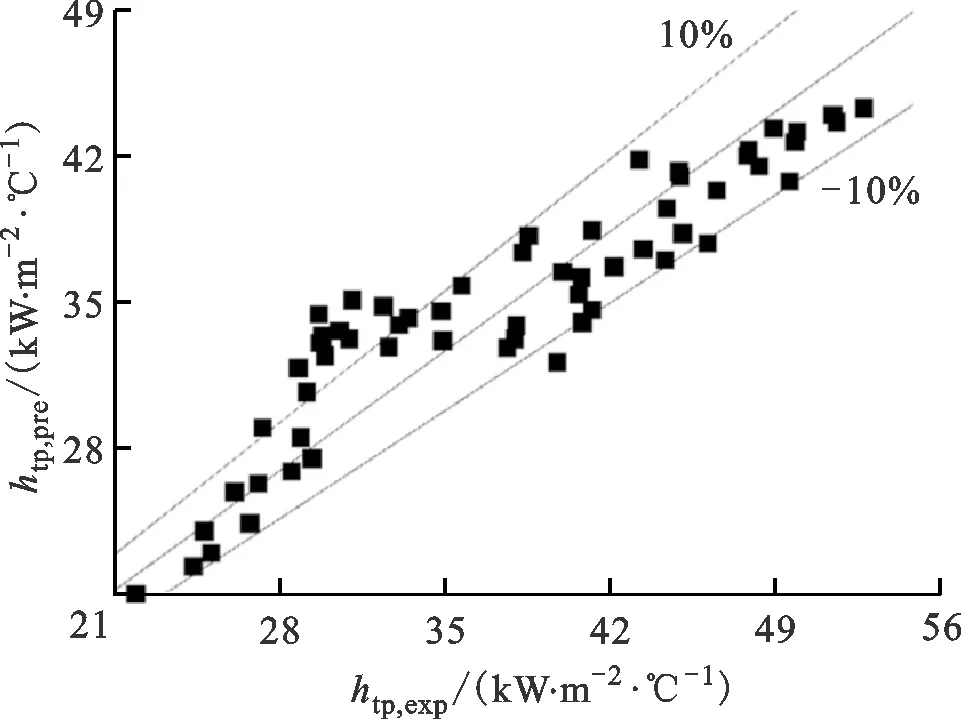
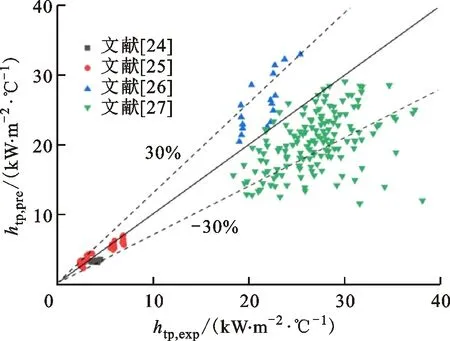
E=1+46B0.5,B<3×10-5,0 (23) E=FB0.5exp(2.74N-0.1),N<1 (24) E=FB0.5exp(2.74N-0.15) (25) F=14.7,B>11×10-5 (26) F=15.43,B<11×10-5 (27) 为比较5个关联式对试验数据预测性能的影响,引入以下3个参量。 平均误差为 (28) 平均绝对误差为 (29) 标准偏差为 (30) 式中:n为试验数据个数;σi通过下式计算 (31) 图11为5个关联式与试验数据的对比图,htp,exp为试验所得两相传热系数,htp,pre为各经验关联式计算得两相传热系数。 改进后的关联式如下 (32) (33) (34) 表3为5个现有以及改进后关联式对试验数据预测性能的影响。 通过对图11和表3进行分析,5个经验关联式中,Liu公式在对矩形通道内沸腾传热特性变现出较好的预测性能,有97.6%的试验数据落在了20% 表3 关联式传热系数预测性能比较 (a)Chen公式 (b)Liu公式 (c)Cooper公式 (d)Kim公式 (e)Shah公式 (f)改进后的关联式图11 现有与改进关联式试验数据对比图Fig.11 Comparison of existing and improved correlations 范围内,全部落在了30%的范围内,标准偏差为11.8%,表明预测结果与试验数据之间偏离程度较小;除了Liu公式,Shah公式预测性能较好,Cooper公式次之。改进后的Kim公式平均误差、平均绝对误差和标准偏差分别为1.4%、7.8%和9.6%,其中77.1%的数据点落在了±10%误差范围内,与原关联式相比预测效果改善明显。在图11f中,13.6%的试验数据落在了与试验数据偏差10%范围外,存在偏差的数据试验工况为不同压力和质量流速下入口温度为试验段出口刚饱和时的传热数据。通过热平衡方法计算的流体状态已经饱和,但是实际上的饱和沸腾发生的位置比热平衡计算位置更加延后,实际该位置处于过冷沸腾阶段,得到的传热试验结果比预测值低,而充分沸腾后的数据不会和改进后的偏差过大。因此,不同尺寸窄矩形通道内如何准确确定饱和沸腾起始点是一个待解决的问题。 图12为改进后的关联式与现存文献中试验数据对比图[24-27]。从图12可以看出,改进后的关联式可以在一定范围内较好的对现存文献中的数据进行预测,75%的预测数据落在了与试验值偏差±30%范围内。还有一部分存在较大偏差可能是以下原因导致:首先是矩形通道间隙的影响,在一定条件下气泡从壁面脱离直径一定,随着通道间隙的变化,通道内气泡行为及流型可能发生相应的变化,从而使得预测值和试验值出现偏差;其次试验系统的压力与临界压力的比值也会对关联式的预测性能产生影响,文献[24]和[25]压比在本文压比范围内,不同于本文,文献[27]中试验工况压力范围为0.13~0.26 MPa;最后文献[27]中偏差超过30%,试验数据大部分质量流速为400 kg/(m2·s),较本文质量流速较低,在不同间隙的矩形通道内低质量流速对传热的影响可能存在差异。因此为进一步了解矩形通道内沸腾流动传热特性,还需展开对不同间隙、不同压比和不同质量流速条件下矩形通道内传热特性的研究。 图12 改进关联式与文献数据对比图Fig.12 Comparison between improved correlation and literature data 本文通过试验的方法研究了入口压力2.1~10 MPa、质量流速1 000~1 500 kg/(m2·s)、热流密度100~300 kW/m2、通道尺寸宽高比39.4时,并联矩形通道中不同参数对通道内换热特性的影响,并与已有换热经验关联式进行对比,试验结果为船舰核反应堆堆芯热工水力设计、安全分析、性能预测及结构完整性评估和优化提供参考,得出如下主要结论。 (1)流体饱和沸腾发生后,质量流速对换热特性的影响减弱,传热系数受质量流速影响不大,热流密度对沸腾传热影响较大,流体换热系数随着热流密度的增加而增加:此变化趋势反映出,当热力学干度低于0.15时,核态沸腾在换热过程中起到主导作用。 (2)分析了并联矩形通道内流动分配问题。通过对比相同位置、相同工况下的传热系数及壁温分布,发现并联矩形通道间的最大差值不超过±7%。因此,从传热特性来看,两个并联通道间未存在明显的流动分配问题。 (3)和5个已有关联式换热特性预测性能对比,发现基于Chen类型的公式较其他类型公式具有较好的换热预测性能,其中精度最高的为Liu和Winterton公式,对传热系数预测的平均误差、平均绝对误差和标准偏差分别为-7.2%、10.0%和11.8%,其中61.4%的数据点落在了±10%误差范围内;并以Kim公式为基准,得到预测精度更高的关联式,改进后的公式分别有77.1%、96.4%的数据落在与试验数据偏差±10%、±20%范围内。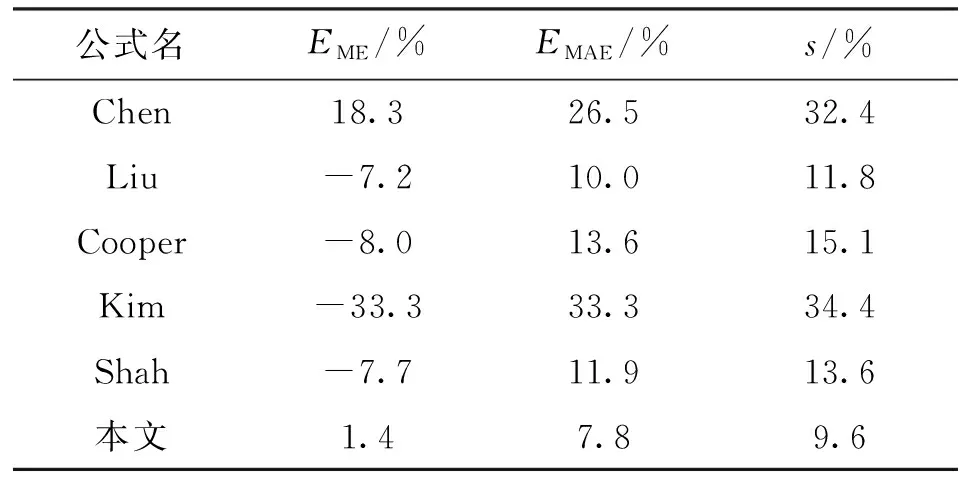
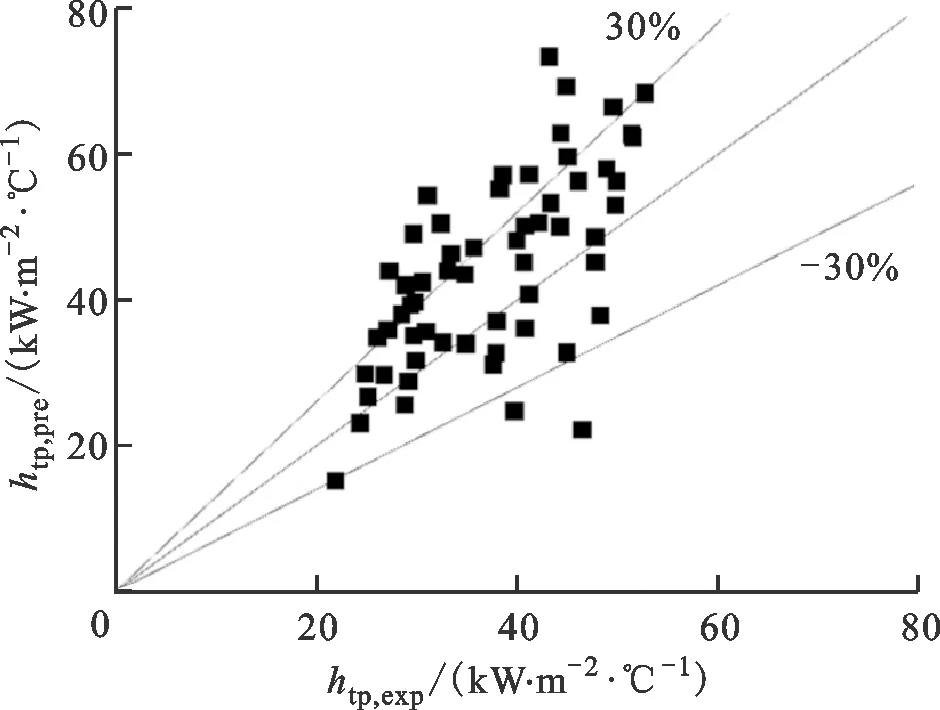
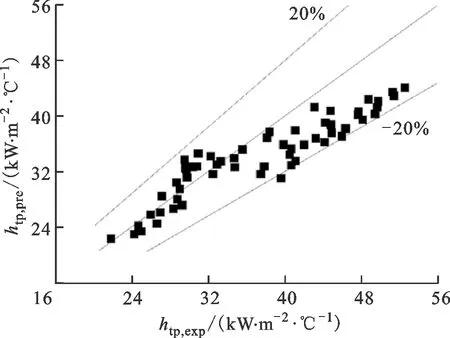
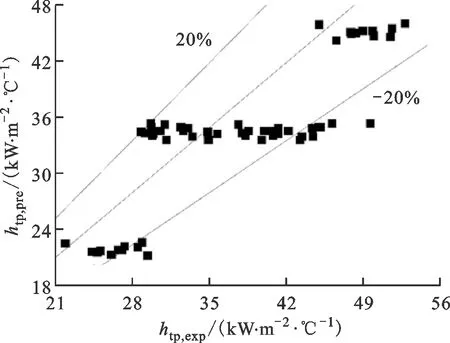
3 结 论
