传热学与电学问题的迁移类比研究:(2)工程实践

2021-09-10李元王晨张冠军

西安交通大学学报 2021年9期

李元,王晨,张冠军

(1.西安交通大学电气工程学院,710049,西安;2.西安交通大学电力设备电气绝缘国家重点实验室,710049,西安)

前文[1]详述了传热学与电学迁移类比研究的理论基础,并借助热电理论类比得到热路模型。为验证上述研究的正确性与适用性,本文给出两个运用热-电类比思想解决电气工程领域中热场估算等典型问题的分析案例。

电力设备是构成电力系统的基本元件,在电能产生、输送、变换和利用等环节中起到关键作用。电力设备在使用过程中受负荷波动影响,常因过热导致故障,从而威胁电力系统的安全可靠性[2]。因此,研究电力设备内部与外部的传热过程,严格控制其运行温度,合理确定负荷限值,对保证设备的绝缘强度、稳定性和高可靠性具有重要意义。

目前,随着输电电压等级的提升、设备小型化的需求以及新型设备的出现,电力设备的容量体积比不断增大,内部结构与组成日趋复杂,计算设备内部热场分布变得更加困难,如何快速准确地计算设备内部温度,进而有效评估设备负载能力成为电气工程特别是高压输电领域的一个重要研究方向。

本文以电力电缆与电力变压器为研究对象,针对估算特殊区域电缆载流量与快速有效预测变压器热点温度的问题,运用热路模型法对局部穿过不利散热区电缆的稳态载流能力与油浸式变压器的热点温度开展研究。通过算例验证该方法在快速估算热场方面的有效性,展现热-电迁移类比思想潜在的工程实践价值。

1 电力电缆的载流能力研究

1.1 问题:如何估算特殊区域电缆载流量

随着城市化建设速度加快,大城市中心用电负荷陡增,城市建设规划与架空输电走廊相互配合的矛盾日益加剧[3]。有序开展大规模电力架空线路“入地”工作成为现代都市建设的重要方向。以深圳为例,目前配网电缆化率为88%[4],中心区罗湖、福田、南山已基本实现电缆全覆盖,达到99%以上,地下电缆输电线路取代架空输电线路成为今后的必然趋势,尤其是在城镇市区。

(a)土壤直埋 (b)沟槽式

(c)管道式 (d)隧道式图1 常见的电缆敷设方式Fig.1 Typical laying methods of cable

常见的地下电缆敷设方式主要有土壤直埋、沟槽式、管道式(排管)和隧道式[5],因不同电压等级和敷设环境而异,如图1所示。计算4种常规敷设方式下电缆的稳态载流量时,可直接依据国际电工委员会(IEC)IEC60287标准[6-7]推荐的公式。在城市电网大规模建设中,受实地条件限制,一些非标准电缆敷设方式大量使用。例如,电缆通常沿街道走向敷设,有时需要穿过街道或建筑物,导致局部电缆运行环境发生改变[8]。为了保护电缆,往往将局部电缆敷设在管道内,其他区域仍以直埋方式敷设,如图2所示。采用管道敷设区域的热阻通常高于周围环境介质的,对电缆散热产生不利影响,需重点关注穿过不利散热区时电缆的温度分布与载流能力,防止过热事故。目前,IEC标准推荐方法仅适用于标准敷设情况,非标准敷设情况下的电缆载流量计算尚缺乏科学的计算依据。

图2 电缆穿过街道的敷设方式Fig.2 Cable laying method through streets

第1节依据文献[1]所述的热-电类比迁移思想,研究了一种典型的非标准敷设情况——穿过不利散热区域的电缆温度分布与载流量,研究建立的计算分析模型可为电缆非标准敷设方式下温度场与载流量评估提供解决方案。

1.2 基于分布参数的电缆热路模型

35 kV及以下电压等级电缆多为三芯结构,典型结构如图3所示。电缆的发热源主要有导体电阻损耗W1、绝缘层介质损耗W2、金属护套电阻损耗W3与铠装层电阻损耗W4[9]。当电流通过电缆导体时,不利散热区与正常敷设区电缆的径向传热过程基本相同。导体电阻产生焦耳热损耗引起导体温升,产生的热量部分储存在导线和绝缘材料内,其余热量经绝缘材料传导至电缆表面和周围介质,最后土壤与空气边界产生对流与辐射换热。经过一个较长的暂态过程,电缆的温度逐渐达到稳定,产热与散热达到平衡。基于电缆径向传热过程建立的热路模型如图4所示。图中,R1、R2、R3和R4分别为导体与金属套间热阻、金属套与铠装间热阻、外护层热阻、外部热阻。各部分热阻依次连接,形成串联热路。

1—导体;2—导体屏蔽;3—绝缘层;4—绝缘屏蔽;5—金属套;6—外护层;7—内衬;8—铠装层。图3 交联聚乙烯电缆结构Fig.3 Structure of XLPE cable

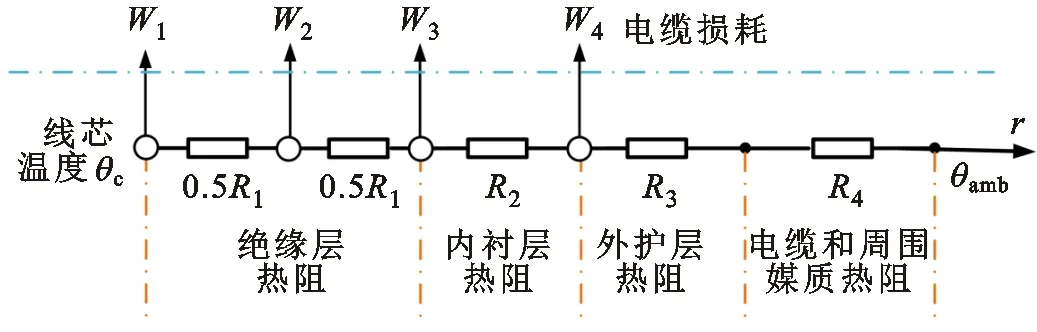
图4 电缆径向热路模型Fig.4 Radial thermal circuit model of cable

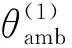
图5 穿过不利散热区电缆的热路模型 Fig.5 Thermal circuit model of cables crossing unfavorable heat dissipation regions

1.3 载流量计算与实例应用

根据能量守恒定律,电缆导体长度为dz的微元体在任一时间间隔内有动态平衡关系

(1)

(2)

将参数Wc的表达式代入式(2),整理化简可得

(3)

(4)

式中A和B是两个任意常数。根据边界约束条件解出A和B,即可得到轴向导体温度的表达式

(5)

式中z0为不利散热区宽度的1/2。设置θ(1)(0)为电缆导体最高工作温度,迭代计算电缆稳态载流量和对应的电缆轴向温度分布。

以YJV8.7/10 kV 3×300 mm2的XLPE电缆为例,应用图5提出的模型与表达式估算电缆温度分布与载流量。若该电缆为正常敷设,载流量应为475 A。若穿过不利散热区,局部电缆段穿过宽15 m的街道,从街道中心位置即z=0处开始分析导体轴向温度分布,计算结果如图6所示。

图6 电缆轴向导体温度分布Fig.6 Axial temperature distribution of cable conductor

由图6可知:敷设于不利散热区的电缆导体温度较高,最高温度出现在街道中心位置,达到146.9 ℃;不利散热区的边界处(即z=7.5 m附近)电缆导体温度变化急剧;正常敷设区的电缆导体温度相对较低,距离街道中心15 m时,导体温度降至稳态最高工作温度90 ℃。经迭代计算得到此时电缆的稳态载流量I=369 A,比正常敷设下的载流量降低23%。该研究对电缆线路合理敷设、负荷动态实时调整与电缆经济安全运行具有参考意义。

2 电力变压器的热点温度预测

2.1 问题:如何快速有效预测热点温度

电力变压器是电能转换的核心设备,结构非常复杂,在电力系统中作用重大。目前,用电需求量快速增长,而电网规划与建设相对滞后,使得部分变压器在较高的负荷率下运行[12]。2019年某省电网年度运行方式电网风险报告显示,变电站内一台220 kV主变压器跳闸后,可引起区域网络内53台主变压器负载率超1.3。变压器的负荷增大会引起负载损耗增加、内部温度升高,从而导致绝缘强度降低,变压器的故障概率显著上升。一旦变压器停运可能引起电网大面积停电或限电,造成恶劣的社会影响[13]。为了延长变压器的运行时长,保障电网的安全可靠性,许多学者聚焦变压器的热特性研究[14-16]。对热特性的研究集中在绕组热点温度的预测,即变压器绝缘系统承受的最高温度[17]。

准确监测、管控热点温度可有效评估变压器的负荷能力,延长变压器寿命。光纤传感器或热电偶测量绕组温度是最直接获取变压器内部温度的方法[18]。直接测量法简单易实现,但存在部分局限:将探头埋入变压器绕组线饼中可能会降低变压器的绝缘强度;测温元件埋设位置与数量的不确定性使得测温结果存在误差;高质量的传感器设计和工艺制造要求增加了生产与维护成本。除此之外,学者们还研究了一些其他方法:标准推荐法[19]通过描述变压器内部热传递过程来间接估计热点温度,但是公式中多为经验参数,计算误差较大;数值计算法[20]计算精度高但计算复杂且耗时长,不适合工程应用;人工智能法[21]预测精度高但训练过程易陷入局部极小值点。为实现快速有效预测变压器热点温度,本节在热-电迁移类比思想的基础上,提出将变压器内部热传递过程简化为热路模型,进而依据电路理论估计热点温度。

2.2 基于集总参数的变压器热路模型

变压器的热源主要由负载损耗、空载损耗和器壁吸收的日照辐射功率组成[22]。负载损耗产生的热量首先传导至铁芯与绕组,使二者温度升高。此时,铁芯与绕组和绝缘油间存在温度差,热量以热对流的形式传递到油中,吸收热量的油温度升高、密度减小,向箱体顶部流动。顶部绝缘油在日照辐射的作用下温度也会升高,由于此部分影响通常小于内部损耗发热,顶部油温相对较低,因此顶部绝缘油会向底部运动,上升的底部油流与向下的顶部油流形成热对流。其中,靠近变压器箱体的绝缘油将这些持续产生的热量传递到冷却装置和变压器外壳。因此,冷却装置和变压器外壳温度升高,与周围空气产生温度差,热量最终以热对流和热辐射的形式传递到外界环境,变压器内部热量传递过程如图7所示。

图7 变压器内部热量传递过程Fig.7 Heat transfer process in transformer

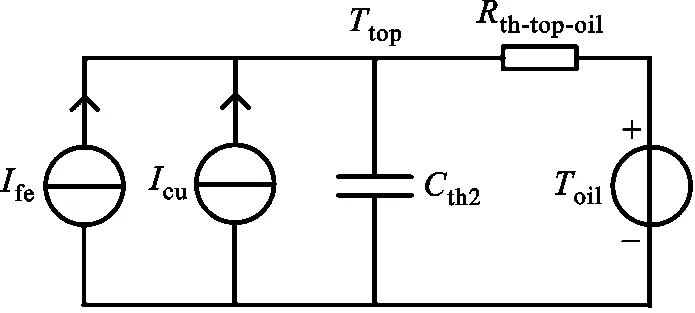
基于变压器传热过程和热-电类比理论,建立了环境温度-平均油温-顶层油温到绕组温度的变压器集总参数热路模型[23-24],如图8所示。以图8a为例,分析热路模型的建立过程。在变压器空载损耗Ife、负载损耗Icu与变压器外壳吸收的日照辐射功率Isun的共同作用下,绝缘油温度升高,直接影响平均油温Toil,因此可将三支热流并联。在热量传递的过程中,铁芯、绕组、绝缘油与变压器外壳的温度都上升,可看作是热量的储存,用热容Cth1表示;在绝缘油、变压器外壳及外部空气温度的影响下,热量的传递会受到阻碍,用热阻Rth-oil-air表示。完整的散热过程是在平均油温与环境温度的温差的驱动下进行的,因此可将环境温度Tamb看作电压源。

(a)环境温度-平均油温模型

(b)平均油温-顶层油温模型

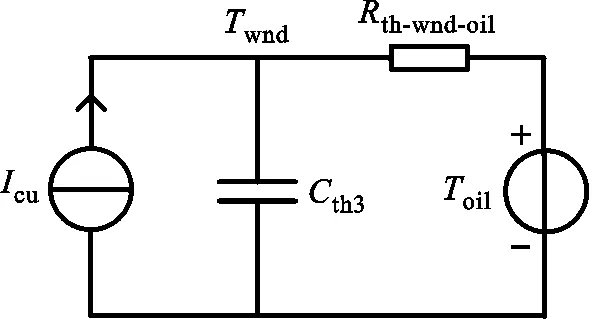
(c)平均油温-绕组平均温度模型图8 变压器热路模型Fig.8 Thermal circuit model of transformer

图8b与8c涉及到的其他物理量有:Ttop、Twnd分别表示顶层油温与绕组平均温度;Cth2表示铁芯、绕组和绝缘油的总储热热容;Cth3表示为绕组的储热热容;Rth-top-oil表示在顶层油温至平均油温的散热过程中,绝缘油对散热过程的阻碍作用;Rth-wnd-oil表示在绕组平均温度至平均油温的散热过程中,绕组和绝缘油对散热过程的阻碍作用。

2.3 热点温度估算方法与实例验证

将电路中的基尔霍夫电流定律类比应用于热路模型,可得到图8对应的一阶微分方程

(6)

(7)

(8)

已知环境温度Tamb,可由式(6)求得平均油温Toil,进而可通过式(7)(8)分别求解Ttop与Twnd。

为了便于分析变压器内部温度场分布,GB/T 1094.7—2008负载导则[25]给出了经过合理假设与简化后的变压器内热分布,如图9所示。图中:gr为绕组平均温度Twnd与平均油温Toil的差值,绕组热点温度通常高于绕组顶部温度;H>1为热点系数;Hgr为热点温度Ths与顶层油温Ttop的差值。

图9 变压器内热分布Fig.9 Heat distribution in transformer

由此,得到变压器热点温度的计算公式

Ths=H(Twnd-Toil)+Ttop

(9)

采用110 kV/50 MV·A油浸自冷型变压器与220 kV/180 MV·A油浸风冷型变压器的温升实验数据,对图8提出的温度估算模型进行验证,预测结果如图10和11所示。

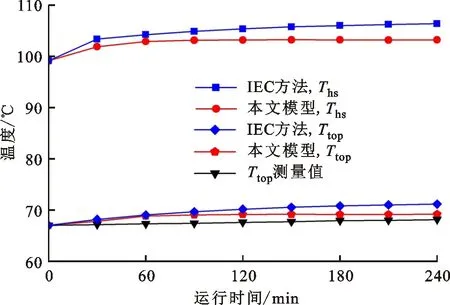
图10 110 kV变压器的实测数据与模型验证Fig.10 Model verification for a 110 kV transformer

分析图10可知,采用IEC推荐方法计算热点温度的最大绝对误差和相对误差分别为3 ℃和4.47%,而本文模型计算结果的最大绝对误差和相对误差分别为1.5 ℃和2.14%。分析图11可知,对比220 kV变压器的实测数据,IEC推荐方法计算结果的最大绝对误差和相对误差分别为3.6 ℃和4.11%,本文模型的最大绝对误差和相对误差分别为1 ℃和1.1%。可以看出,本文提出的变压器热路模型在简化传热计算过程的同时,具有很高的准确度,便于工程应用。

图11 220 kV变压器的实测数据与模型验证Fig.11 Model verification for a 220 kV transformer

3 讨论与展望

本文介绍了热-电类比迁移思想在电气工程领域应用的两个典型案例,运用电路基本理论实现热路模型的快速准确求解,从而简化工程中的复杂传热问题。除此之外,热-电类比思想也已开始应用于其他领域。例如:微机械领域通过构造导热等效模型模拟微流体器件的响应时间,进而评估其工作性能[26];建筑空调设计中考虑到传统谐波法数学推导的复杂性,运用热-电类比理论简化墙体温度响应的计算过程[27];光学传感器研制中,常通过建立等效热网络分析和优化光纤环模块的热特性[28]等。

物理学史的发展历程证实了分支学科间物理概念或数学形式的相似性并非偶然,这些相似性源于物理学的统一性。在理解传热学与电学中许多基本物理量具有内涵与表达式对偶关系的同时,也要注意到两个学科的类比研究还有不少热点值得继续探索。例如,相较于电路中的电感,传热学中尚无热感的概念,热场中是否存在与热量交互变化的某种作用能量或作用力仍待探究。另一方面,随着研究的深入,出现了许多非常规条件下的传热问题(如非线性和非平衡因素较强的场合、微细时间或空间尺度),傅里叶定律等传统线性导热定律的适用性存在挑战。如何通过理论间的融合与交叉合理解释非常规传热现象、完善传热理论需要进一步的研究。

本文基于传热学与电学的诸多共性,提出热-电迁移类比思想用于解决部分实际工程问题。迁移类比思想同样适用于探索各个物理分支学科间的共性规律。因此,期望更多学者专注研究本学科方向的同时,亦关注其他分支学科的发展,从中借鉴新的成果,推动学科融合,驱动科技创新。