基于误差反馈的LED阵列近场光强检测

侯启真，马秉正

（中国民航大学 电子信息与自动化学院，天津 300300）

1 引言

发光二极管（light emitting diode，LED）作为21世纪最具有竞争力的新型固体光源之一，凭借体积小、抗干扰性能强等优点，现已被广泛地应用于指示、照明以及特种照明等领域［1～6］。在机场、铁路以及船舶等需要目视助航的地方，为保证远处目标能够有效地识别出助航灯具的同时避免单个大型LED发热严重、影响寿命的问题，通常采用多颗LED按一定规律组合成平面阵列光源的方式［7，8］。以机场跑道警戒灯为例，这类光源的尺寸通常较大，亮度较高，出射角较大，按照光度学相关检测原理可知，在实验室中通常需要大范围的空间完成检测［9～13］。近几年来关于近场光强检测的热度开始兴起，使用近场分布式光度计能有效测量的同时可以节省空间［14～16］，但在算法实现上通常需要积分、全空间检测等步骤，检测周期长且设备价格昂贵。

针对上述方法的不足，本文提出一种基于照度误差反馈的方法，在灯具使用现场的近场条件下，通过设置照度探头进行采样获得一系列的照度数据，然后将面光源拆分成多个子光源，这些子光源可视作点光源，再对这些子光源预设一组光强值并利用此组光强分布计算测量平面上的照度，此时将计算出的照度与利用照度探头测量得到的实际照度进行比较并计算两者之间的误差，然后用这一误差来更新设置的光强分布并再次计算新的误差，多次迭代直到计算出的照度值与实际测量得到的照度值之间的误差足够小，此时设置的光强值便能与灯具的实际光强分布近似相等，最后利用MATLAB进行仿真验证该方法的可行性。通过这一方法能够设计一个可以在现场进行使用的系统，快速准确地在近场完成灯具的光强检测工作，同时保证系统可设计为便携式，解决维护人员在巡检时检测手段匮乏，精度不够准确等问题。

2 光度学检测原理

光源在指定方向上的发光强度是该光源在包含指定方向的立体角元dΩ内传输的光通量dΦ，除以该立体角元之商，单位为cd（坎德拉），即：

表面上一点处的光照度是入射在包含该点的面元上的光通量dΦ除以该面元面积dA之商，单位为lx（勒克斯），即：

又因为空间角与被照射面之间满足dΩ ＝dA·cosθ／r2，所以光强与照度之间满足下式：

即距离平方反比定律，式中θ为入射光线与平面法线之间的夹角，如图1所示。

图1 距离平方反比定律Fig.1 Inverse law of distance square

3 基于照度误差反馈计算光强

光源的发光强度空间分布通常是将光源视作点光源进行分析讨论的，其分布特性与空间角有关，在实际上并不存在真正意义的点光源，一般当探测元件离光源足够远使得距离平方反比定律近似满足时，将光源近似看成点光源，这一条件即前文提到的远场条件，这也是传统光强检测所常用的条件与方法。相反的，在这一距离条件不满足时，称为近场条件。通常情况下，将探测距离为光源最大尺寸5倍时视作远场条件。助航灯具在工作时即可被远处的飞行员视作点光源。

然而使用远场条件在现场针对具有较大尺寸的灯具（如跑道警示灯）进行检测时，尤其是在这类灯具的使用现场、灯具不拆卸、不移动的情况下需要探头在大范围的空间上进行移动、采样，这样不能使得整个测量系统做得足够便携，因此应考虑在近场条件下进行光强的检测工作并通过在近场的相关计算推导出灯具远场情况的光强分布。

以LED阵列面光源为例，其光强分布除了作为一个整体在远场条件下通过距离平方反比获得外，还可以通过得到每个LED的光强分布并计算在同一空间角方向上的光强之和得到，即：

式中：IΣ为LED阵列的光强分布；Ii为阵列中第i个LED的光强分布；α为指定方向与阵列所在平面的法线之间的水平夹角；β为指定方向与阵列所在平面法线之间的垂直夹角。

在5倍LED阵列面光源最大尺寸以内进行测量时，各LED可视作点光源，测量点的照度由所有LED在测量点上形成的照度叠加而成［16］，如图2所示，使用距离平方反比定律可知测量点的照度数据如式（5）所示。

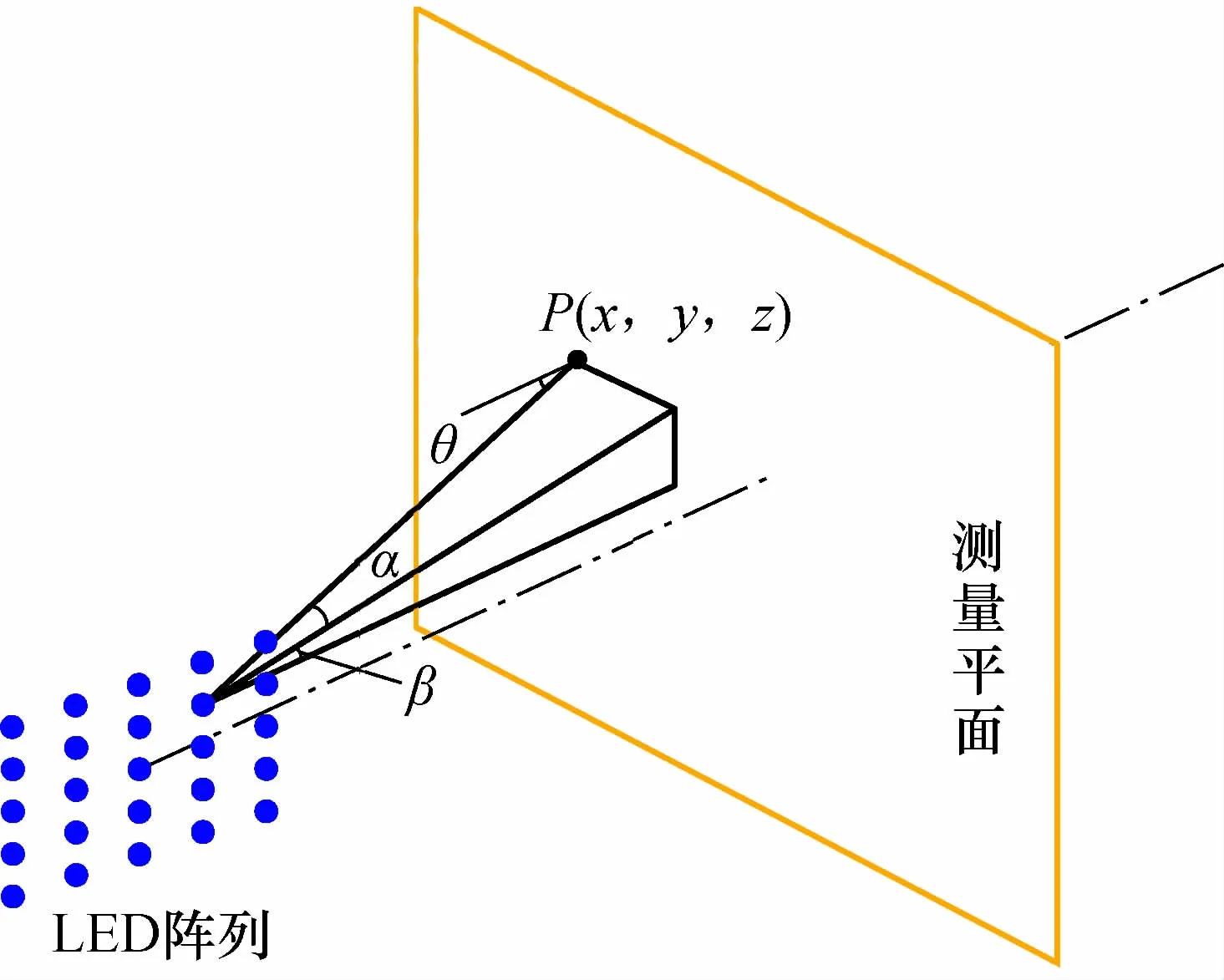
图2 第i个光源在测量平面上测量点P处的照度Fig.2 The illumination of the ith light source is measured at point P on the measuring plane

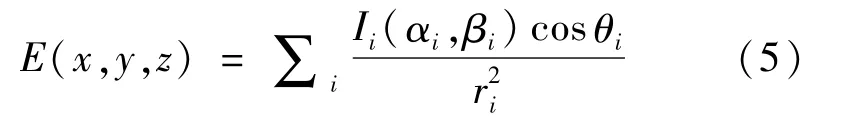
式中：E（x，y，z）为测量点P上的照度值；x，y，z为测量点的空间坐标；αi，βi分别为第i个点光源到测量点的向量在水平、垂直方向上夹角；θi为第i个点光源到测量点的向量与测量平面的法线之间的夹角；ri为第i个点光源到测量点的距离。

对式（5）进行分析能够发现，当各LED的光强分布和各点空间位置已知时，可以通过式（5）推导出空间中任意位置的照度；但当各LED的光强分布未知，仅知道近场区域内的照度分布和光强与各测量点的空间位置时无法利用式（5）进行反推。这是因为在进行反推时已知条件仅有等式左边的叠加和，等式右边则存在无穷多个可行解，这也就意味着两个除了光强分布不同其他条件完全相同的LED阵列可能在近场区域内形成同样的照度分布。假设阵列中各LED光强分布相同且满足类余弦分布进行反推，即Ii＝I0*cosmαi*cosnβi时，其中I0为光强最大值，α和β分别为偏离光轴的水平夹角和垂直夹角。需要求解的未知量有I0，m和n，理论上求解可行，但由于m和n在指数项上，而且此时在测量平面上的照度为叠加和，对于m和n不易直接求解，使用拟合逼近的思路对m和n求解计算量较大。因此提出一种利用照度误差反馈的方法，将预设的光强分布逼近实际的光强，从而实现在近场条件下利用照度与空间位置对阵列光源远场情况下光强分布的近似求解。

通过上述分析可知，在灯具使用现场，因为所有LED构成一个整体，无法通过测定单个LED的光强分布来计算得到阵列面光源的光强分布，每个LED的光强分布情况未知且各自相同与否同样未知；而且此时测量点的照度值为叠加和，不能直接使用距离平方反比定律进行光强计算也无法通过简单的假设各个LED的光强分布相同进行计算。因此本文设计了一种基于照度误差的方法，在LED阵列面光源工作时的近场区域内选定一个与面光源平行的平面作为测量平面，通过照度探头进行移动、采样得到一系列的照度；然后对这些LED各自预设其光强分布并利用此组光强分布计算测量平面上的照度；再将计算出的照度与利用照度探头测量得到的实际照度进行比较并计算两者之间的误差，将误差反馈用以更新各LED的光强分布，迭代多次至误差足够小以求得各个LED的近似光强分布，从而得到整个LED阵列面光源的空间光强分布。具体操作流程如图3所示。

图3 光强检测流程图Fig.3 Flow chart of light intensity detection

首先在近场区域内设置一个平面作为测量平面并通过移动照度探头进行采样得到其照度分布情况，再通过该测量平面与灯具出光口平面之间的空间几何关系得到每个测量点和每个LED的空间坐标，目的是为了能够计算每个LED在测量点处对应的空间角与距离。然后给每个LED预设一个初始的光强分布，通过式（5）计算出某一测量点上的照度值，再计算这一照度与实际照度之间的误差Δ：

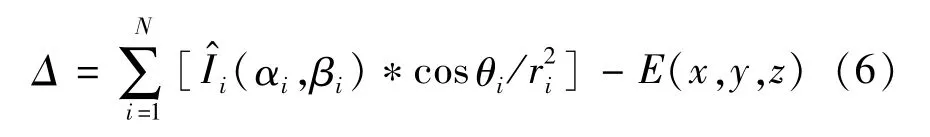
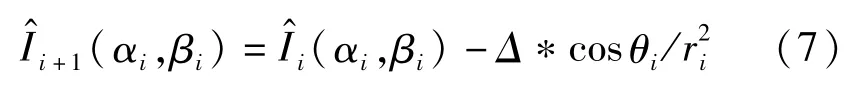
接着再次代入式（6）计算误差，代入式（7）更新设置的光强值，多次迭代至计算照度与实测照度之间的误差足够小，此时得到的各LED在这一测量点对应空间角上的光强值近似等于其实际光强。通过将近场足够多的测量点按上述方法进行计算并记录后，能够得到每个LED的近似光强分布，最后再将各LED的光强分布在同一空间角下的值进行求和即可得到阵列的整体光强分布。

此外，对于LED阵列面光源而言，在生产、组装的过程中，每个LED的实际光强分布不一定彼此相同，存在个别或多个LED的光轴偏离面光源法线、中心光强偏大或偏小等情况。在进行仿真验证本文方法的可行性后，对上述特殊情况同样进行了仿真计算，进一步验证了可行性与适用性。

4 近场测量仿真

以9×9方形LED阵列为例对本文所提出的方法进行仿真验证，在TracePro中设置其分布方式如图4所示，在近场条件下的光斑如图5所示。

图4 用TracePro设置9×9方形LED阵列Fig.4 Setting the 9×9 square LED array by TracePro

图5 近场条件下的光斑Fig.5 Light spots in near-field conditions

设置各LED点光源的光强分布为（8）：

式中：Ii为第i个LED的实际光强分布；I0为光轴上的光强值；αi，βi分别为第i个LED在指定方向上与光轴之间的水平夹角与垂直夹角。其中：m＝80，n＝70，即在水平方向上半值角约为7.5°，在垂直方向上半值角约为8°。为保证测量平面上照度存在叠加现象，将阵列设置为关于xOy平面原点对称的结构，各LED之间的水平、垂直距离da与db均设置为0.03 m，光源平面与测量平面之间距离d为1 m，此时的测量平面大小选定为60 cm×60 cm。

由式（5）可知，在测量平面上其照度分布可进一步表示为：

式中：αi、βi、cosθi、可换算坐标至式（10）所示。

式中：x，y为测量平面上测量点的坐标；xi，yi为第i个LED的坐标。用MATLAB进行仿真，将整个阵列作为点光源按照距离平方反比初步计算阵列的光强分布如图6所示。

图6 LED阵列实际光强分布与初步计算的光强分布Fig.6 The actual intensity distribution of LED array and the preliminary calculation of the intensity distribution

在上述近场条件下，图6中初步计算的光强分布与实际的阵列光源光强分布存在很大的偏差，为了保证后续的误差反馈过程能够迭代出与实际光强分布有较小误差的测量值，将这一计算结果按照LED的个数进行等分并向光轴位置进行收缩，之后就能够得到一个在所有角度上都小于实际光强分布的预设光强分布并以此光强分布进行后续计算。计算结果如图7所示。

图7 收缩之后的单个LED预设光强分布与单个LED实际光强分布Fig.7 The default light intensity distribution of a single LED after shrinkage and the actual light intensity distribution of a single LED

选用某一测量点将预设的各个点光源光强分布代入式（6）计算理论照度与实测照度的误差Δ。

再将误差Δ代入式（7）用以更新设置的各个点光源在测量点所对应角度下的预设光强值，多次迭代至测量点理论照度与实测照度之间误差足够小，此时可知各个点光源在对应测量点方向的近似光源值。然后将整个测量平面上的采样点逐一进行上述计算后可得到阵列光源的近似光强分布与实际光强如图8所示。

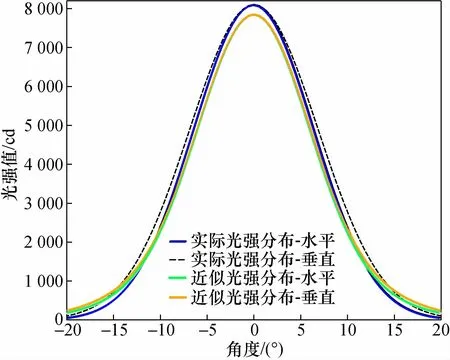
图8 阵列的近似光强分布与实际光强分布Fig.8 The approximate intensity distribution of the array and the actual intensity distribution

根据文献［17］中提出的计算方法，对近似求出的光强结果进行匹配度的计算，如式（11）所示，式中θ，ψ为测量点与光源中心在空间所成的角度。

该匹配度是指两组光强分布数据之间的“拟合优度”，对两组光强分布在相同角度下进行比较。当匹配度超过98%时为优秀的结果，当匹配度超过99%为特别优秀的结果。经过实验比较，一般当匹配度超过90%时检测结果便与灯具的实际光强分布近似，可以接受。

最终计算出此时的匹配度为95.2%，均方根误差为94.61，而直接使用距离平方反比时其匹配度仅为85.6%，均方根误差为268.18；由此可知本文计算方法虽未达到优秀结果的水平，但相较传统方法误差已减少许多且在实际应用时可接受。不过上述情况为LED阵列光轴为垂直于光源平面且每个LED的光强分布都相同的情况。在实际生产与安装中，在光轴和光强分布上彼此之间存在一定差异。设置各LED点光源光轴不同、中心光强相同，光轴相同、中心光强以及两者都不同的3种情况进行进一步分析。

4.1 各LED中心光强不变，但部分LED光轴发生改变时

在程序中随机挑选一部分LED，使其在水平、垂直或者两者都有随机的偏差，空间位置关系同上，在进行仿真计算后求得近似光强分布与实际光强分布如图9所示。

图9 部分LED光轴发生改变时阵列的实际光强与计算后的近似光强Fig.9 The actual light intensity of the array and the calculated light intensity when the optical axis of some LEDs are changed

最终计算出此时的匹配度为93.3%，均方根误差为127.55。

4.2 各LED光轴不变但中心光强发生改变时

在程序中随机挑选一部分LED，使其中心光强存在随机的偏差，其他条件不变，在进行仿真计算后求得近似光强分布与实际光强分布如图10所示。

图10 部分LED中心光强发生改变时阵列的实际光强与计算后的近似光强Fig.10 The actual light intensity of the array and the calculated light intensity when the central intensity of some LEDs are changed

最终计算出此时的匹配度为93.1%，均方根误差为141.26。

4.3 部分LED中心光强、光轴存在随机偏差

在程序中随机挑选一部分LED，使其中心光强、光轴或两者均存在随机的偏差，其他条件不变，在进行仿真计算后求得近似光强分布与实际光强分布如图11所示。

图11 部分LED中心光强及光轴发生改变时阵列的实际光强与计算后的近似光强Fig.11 The actual light intensity of the array and the calculated light intensity when the optical axis and central intensity of some LEDs are changed

最终计算出此时的匹配度为93.1%，均方根误差为130.16。

5 结论

针对如跑道警戒灯这类以LED组成的阵列光源，本文提出了一种在近场条件下，仅依靠照度与空间位置关系来计算阵列的光强分布的方法，通过对阵列中的LED的光强值进行预设，计算照度的误差并反馈用来更新这一组预设的光强值，最终实现光强的检测工作。在机场、铁路等需要目视助航的应用领域，信号光源的重要性不言而喻，日常维护工作完全依赖拆卸后的实验室条件下检测使得成本较高，时间较长。针对这类具有较为明显特征的灯具，本文提出的方法能够在不对灯具进行拆卸、移动的情况下完成检测工作，通过仿真对本文方法的可行性进行了验证并通过设置LED阵列的几种不同情况来分析其抗干扰能力。在工程应用现场，本文提出的方法仅需将探测元件经过指定位置并采样记录下此时的照度数据，后续检测可交由上位机进行处理，大大节省、缩减了这类灯具的维护成本与周期。