双相干点光源的空间干涉

王　敏

(东北师范大学 物理学院，吉林 长春 130024)

双相干点光源的空间干涉

王敏

(东北师范大学 物理学院，吉林 长春 130024)

摘要：为深入研究双相干点光源空间干涉的光场分布情况，通过理论推导给出了三维坐标空间下光场的一般数学展开式及各个形状干涉条纹的成因，并给出了实验不易观察的干涉条纹的原因和强度分布的计算机模拟图.

关键词：迈克耳孙干涉仪；点光源；干涉条纹

1引言

迈克耳孙干涉实验是一个重要的大学物理实验，通过该实验，学生对非定域干涉及等厚和等倾干涉现象有了进一步的理解和掌握. 随着迈克耳孙干涉用途的不断扩展，许多关于迈克耳孙干涉实验的现象和问题引起了更深入地关注和探讨. 本文对迈克耳孙干涉实验背后的双相干点光源空间干涉问题进行了分析[1-2].

2理论分析

2.1　迈克耳孙干涉实验

在迈克耳孙的非定域干涉实验中是让激光束经短焦距透镜射向分光板，调整干涉仪即可在光屏上得到干涉条纹. 实验中采用激光光源实现光波干涉的方法是分振幅法. 其原理是从入射透明板的激光光束中，经过板的2个界面多次反射和折射，得到1组反射相干光束和1组透射相干光束[3]. 实验光路图如图1，激光经透镜会聚后可看成透镜焦点S的点光源，分别经分光板G1、补偿板G2、平面反射镜M1和M2，在平面光屏上呈干涉条纹. 干涉条纹实际上是虚光源S1和S2(S分别在M1和M2中的像)在空间干涉的结果. S1和S2相对空间位置决定着平面光屏上条坟的形状，实验调整M1和M2的相对空间位置，实际上改变的是点光源S1和S2的相对空间位置[4]. 双相干点光源(S1，S2)在均匀介质中的全空间干涉曲面和空间任意平面的交线即光屏上所观察到的条纹，所以光屏上干涉条纹是S1和S2全空间干涉的局部.

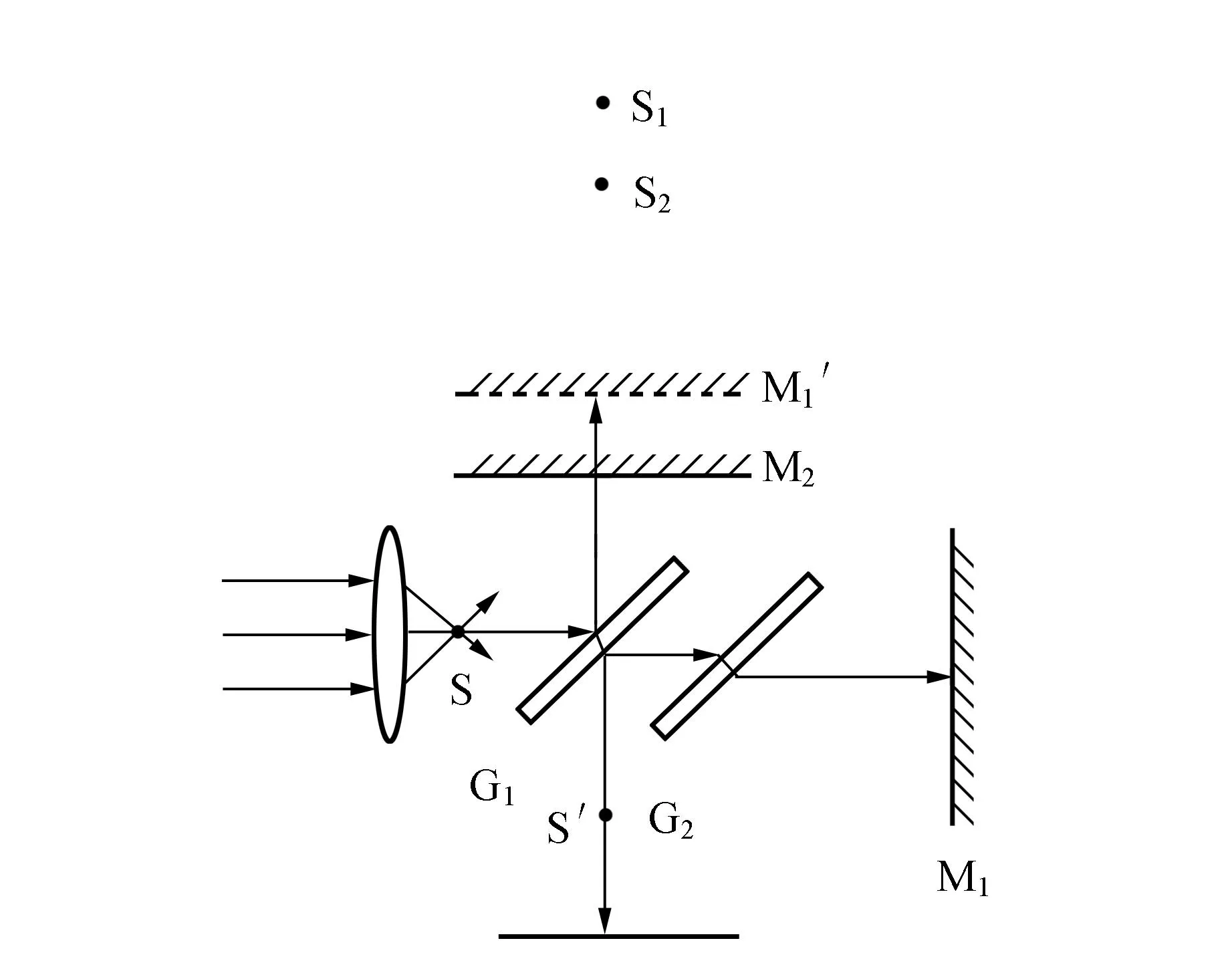
图1　迈克耳孙干仪上的光路图

2.2　相干点光源S1和S2全空间干涉曲面方程

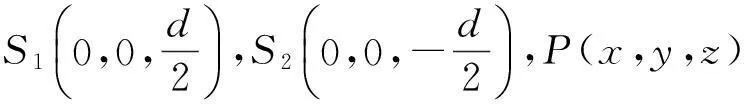
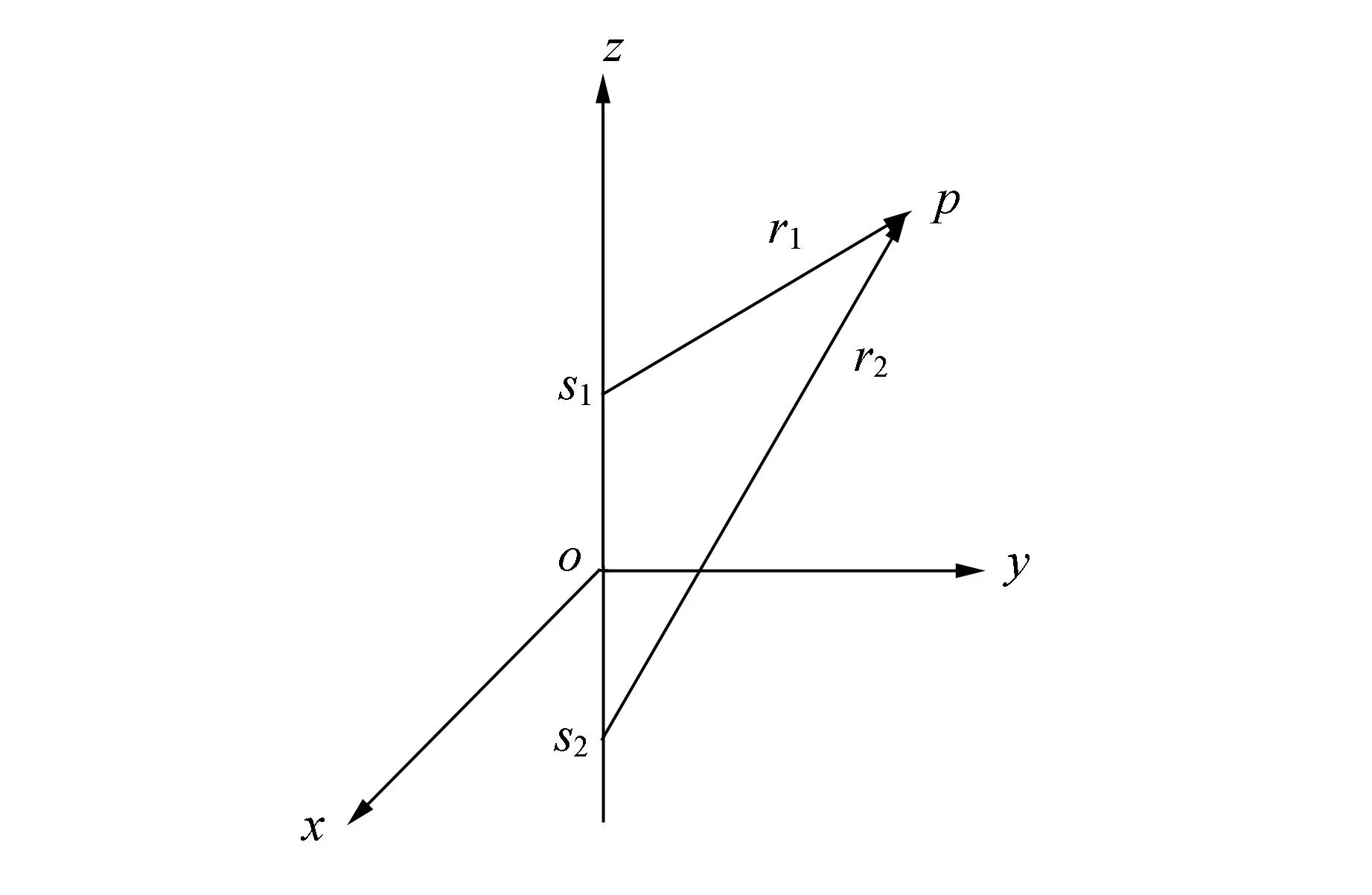
图2　双相干点光源干涉的几何关系

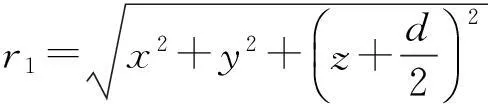
(1)

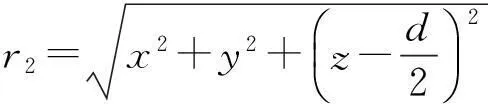
(2)

将式(1)~(2)代入Δ=|S1P|-|S2P|=r1-r2中，整理可得

4(d2-Δ2)z2-4Δ2(x2+y2)=Δ2(d2-Δ2) .

(3)

对式(3)进一步分析:

1)当d2=Δ2时，式(3)可简化为x2+y2=0，即x=0，y=0，z为任意取值，即d为波长整数倍时，z在轴上除线段S1S2外所有点满足相干相长；当d为半波长奇数倍时，满足相干相消.

2)当d2≠Δ2，以干涉相长为例，即d≠Δ(Δ=jλ)由上述式(3)可以得

(4)

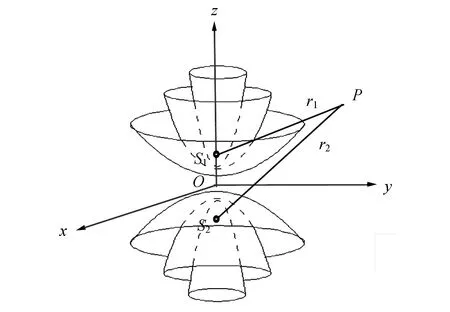
图3　双点光源全空间干涉的干涉场

2.3　光屏处显示的干涉条纹——干涉场在平面上的分布

双相干点光源全空间干涉的旋转双叶双曲面和某一平面相交的交线即为实验所观察到的干涉条纹. 干涉曲面方程和观察平面方程联立得到的是干涉条纹的数学表达式，即平面曲线方程的平面曲线的形状就是干涉条纹的形状. 取不同位置处的观察平面，进一步分析得到如下的平面干涉条纹.

1)圆干涉条纹的成因

屏幕处于z=z0处的截面处时(以亮条纹为例),代入式(4)得

(5)

则干涉条纹为圆条纹，其半径为

(6)

从式(6)看出，随j增大，rj减小. 对式(6)两边平方得

(7)

对式(6)两边取微分

(8)

由此，当屏幕在z=z0截面上时是同心圆，条纹间距与d,z0,j,λ相关.

2)直线干涉条纹的成因

屏幕处于x=x0或y=y0的截面处时,(以亮条纹为例)将条件代入式(4)得

(9)

由式(9)知这是1组双曲线，若干涉级别很小，即d≫jλ时

(10)

若是观察视场很小，即d≪y0，则由式(10)可得

(11)

式(11)即教材中杨氏双缝干涉条纹间距的公式，此时屏幕上呈现直条纹.

3)椭圆和双曲线干涉条纹的成因

若光屏不在上述2种位置上面时，则可得到椭圆或双曲线干涉条纹. 如图4所示，若观察屏的法线位于平面内，且与屏交于(0,y0,z0)点处，设屏所在位置上的点到该点的距离为p，与y轴的夹角为θ，则屏上空间所在的点的坐标为P(x,y0+psinθ,z0-pcosθ)，将其代入式(5)得

(12)

图4　光屏的法线位于zOy平面内的几何关系

整理得

Δ=jλ,

(13)

式(13)可以看做是变量p和x的二次曲线. 当p2和x2前面的系数同号时，曲线为椭圆；当p2和x2前面的系数异号时，曲线为双曲线.

由式(13)可知，出现椭圆条纹的条件为：

即

(14)

若此条件不具备，则将出现双曲线. 分析式(14)可知，当d一定时，θ越大，则干涉级次越高，得到的条纹为椭圆[5].

3理论情况与实际观测的对比分析

3.1　实际观测情况及分析

在实验中，直条纹和圆条纹都可以在理论分析的平面内清晰地观测到，如图5所示. 当S1和S2的连线与接收屏垂直时，观察到同心圆条纹. 当S1和S2的连线与接收屏平行时， 观察到直条

纹. 依据理论分析，该截面的条纹形状实际为双曲线，但是当z=0时，条纹间距符合杨氏干涉条纹间距，而且实际的光屏很小，屏上双曲线的曲率很小，故观察到近乎直线的条纹.

图5　实际观测的条纹形状随位置的变化

实验中，在理论分析的zOy平面上，无论光屏如何放置，都观测不到椭圆和双曲线干涉条纹. 对其进行原因分析，实际情况中因为干涉仪中的接收屏视场很小，所以观察到的最多只是椭圆或双曲线的一部分，也就是弧状条纹[6]. 用光阑来解释，由于干涉区域受到迈克耳孙干涉仪上的分束板和反射镜的限制，等效于在点光源和光屏之间加一大小与分束板和反射镜相同(以最小尺寸为准)的光阑，导致在光屏上观察到的是有限大小的干涉图样,而非双点光源形成的全空间非定域干涉. 用镜像法理论解释，2个等效的点光源为虚像，从它们发射出来的光具有方向性(只朝向光屏方向)，再加上等效光阑的作用，实际空间中只存在双点光源模型所产生的旋转双叶双曲面族的一部分[7]. 所以实验中无法在zOy平面上观察到完整的椭圆和双曲线.

3.2　利用Matlab软件模拟验证干涉场在平面上的分布

虽然实验中很难观测到椭圆和双曲线条纹，但是可以用计算机模拟看清这2类条纹. 利用Matlab对点光源干涉数学模型进行模拟，根据点光源空间干涉光强分布公式(假定从2个点光源发出的是简谐波，且光强不随着传播距离增大而减小)，计算出光强值，再用Colormap和Gray函数转化为灰度值(灰度值可以代表干涉条纹亮暗，比较直观),得到的模拟椭圆和双曲线干涉条纹如图6所示，模拟图样完全符合理论推导.

(a)椭圆条纹

(b)双曲线条纹图6　双相干点光源干涉的计算机模拟图

4结论

双相干点光源模型所产生的干涉场为旋转双叶双曲面族，接收屏所处的位置不同，观察到的条纹形状也不同. 理论情况下，条纹形状有同心圆环、直线、椭圆、双曲线. 但是实际观测中，受接收屏视场大小的影响，干涉场在特殊位置的条纹为直线和同心圆环,一般位置为抛物线型二次曲线族.

参考文献：

[1]汪仕元，朱俊，穆万军，等. 迈克耳孙干涉光程差分析模型探讨[J]. 物理实验，2013，33(3)：31-34.

[2]黄丽，方光宇，宋云飞,等. 迈克耳孙干涉实验条纹计数方法的改进[J]. 物理实验，2013，33(11)：41-44.

[3]顾铮先，卜胜利，童元伟. 浅析“光的干涉”中的光源性质及作用[J]. 大学物理，2013，32(4)：53-54.

[4]姚启钧. 光学教程[M]. 北京：高等教育出版社，2002：19-25.

[5]于建强，袁景和. 双相干点光源干涉的一般分析[J]. 大学物理，2006，25(9)：60-62.

[6]李贤芳，李建青，马争争,等. 基于点光源的迈克耳孙干涉实验条纹的机理分析[J]. 物理与工程，2014，24(3)：37-41.

[7]张汉伟，董天奇. 基于两点光源的迈克耳孙实验分析[J]. 物理与工程，2009，19(6)：34-35.

[责任编辑：郭伟]

Analysis on spatial interference of two coherent point light sources

WANG Min

(School of Physics, Northeast Normal University, Changchun 130024, China)

Abstract:In order to further study the field distribution of spatial interference of two coherent point sources, a generally expanded mathematical formula of light field and the origins of interference fringes in various shapes were given theoretically. The reasons of why the interference fringes were hard to be observed was provided and the computer simulated figures of the intensity distribution was drawn.

Key words:Michelson interferometer; point sources; interference pattern

中图分类号：O436.1

文献标识码：A

文章编号：1005-4642(2015)05-0043-04

作者简介：王敏(1992-)，女，内蒙古包头人，东北师范大学物理学院2011级本科生.

收稿日期：2014-06-05；修改日期：2014-10-09