HSV空间下改进的直觉模糊C均值聚类猪肉图像检测
2021-09-09董素芬
王 迪,董素芬,程 芳,赵 艳,李 今
(河北农业大学 信息科学与技术学院,河北 保定 071000)
1 引言
消费者对畜肉质量和安全问题日益关注,利用计算机视觉技术对畜肉分级的方法种类繁多。其中,图像分割对畜肉分级评定的准确度非常重要。分割图像所采用的方法的鲁棒性、适应噪声的能力和分割效果都对后续畜肉特征提取的有效性有很大影响[1]。
针对传统的最大类间方差法及使用阈值分割和分水岭算法[2]分割图像效果不佳、噪声适应能力不强的问题,以及核磁共振、高光谱成像等无损检测方法大多存在检测仪器体积大、不便于携带、成本高等问题,运用聚类进行图像分割的方法能够获得更好的效果,受到学者们的广泛关注。
在聚类方法中,K均值(K-means)[3]图像分割方法,能够处理非理想环境下的图像,但是Kmeans方法属于硬聚类,对目标图像的边缘处理效果不佳,对图像中的噪声的鲁棒性也不强,不能达到预期效果。而模糊C均值聚类(Fuzzy C-Means Clusterin,FCM)[4]图像分割方法,可以通过优化目标函数得到每个像素点对所有类中心的隶属度,从而决定像素点的类属以达到自动对图像数据进行分类的目的,虽然效果优于K-means方法,但是FCM仍然存在对不确定信息的表达能力不足,不能很好处理聚类的边界异常值以及易陷入局部极小值的问题[5]。
针对以上问题,直觉模糊C均值(Intuitional Fuzzy C-means,IFCM)聚类[6]通过引入隶属度、非隶属度和犹豫度3个参数来表示模糊集,克服FCM算法分割时计算目标函数容易陷入局部极小值的问题。同时对比RGB色彩空间和色调饱和度明度(hue saturation value,HSV)色彩空间,发现HSV色彩空间中V分量受光照的影响最大,H分量基本不受阴影或过高亮度的影响,在HSV空间中对彩色物体进行检测效果会比在RGB空间中更为可靠。
综上分析,本文基于HSV空间提出改进的直觉模糊C均值(HSV relation intuitional fuzzy Cmeans,RIFCM_HSV)图像分割的方法来进行猪肉图像检测,在IFCM 方法的基础上引入了表示图像像素间结构信息的结构函数,将像素间的关系(relation)加入到算法中,从而解决不能很好处理边界异常值的问题,最终实现自然光照中猪肉图像的检测。
2 RIFCM_HSV算法原理及步骤
C均值聚类(C-means clustering)是指,把n个向量Gi(1,2,…,n)分为c个组xj(j=1,2,…,c),并求每组的聚类中心,使得非相似性(或距离)指标的价值函数J达到最小。价值函数公式如式(1)所示:

式中:Ji为组i内的价值函数,Ji的值依赖于Gi的几何特性和ci的位置,d(Xk-ci)为组j中向量Xk与相应聚类中心ci间的欧氏距离。
划分过的组用一个c×n的二维隶属矩阵U来定义,如果第j个像素点Xj属于组i,则U中的元素Uij为1;否则,该元素取0。隶属矩阵公式如式(2)所示:

由于一个给定数据只能属于一个组,所以隶属矩阵U具有如下性质:

该算法通过简单迭代,确定聚类中心和隶属矩阵。
FCM算法将上述硬分类模糊化,引入隶属度函数,定义聚类价值函数,并利用迭代法使其最小化,当算法收敛时,可得到各聚类中心和各个像素点对于各中心的隶属度,从而完成模糊聚类划分[7]。隶属度矩阵U同样满足式(3)的条件约束,FCM算法的价值函数如式(5)所示:
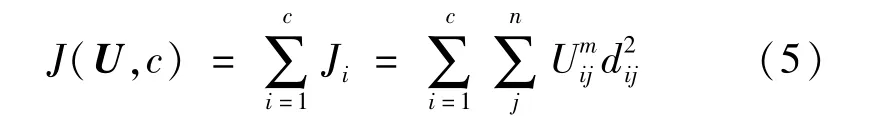
J为c个区域中每个像素到各聚类中心欧氏距离的加权平方和,m为模糊隶属度的加权指数,Uij介于0,1之间为第i个聚类中心与第j个像素点间的欧氏距离[8],ci为模糊组i的聚类中心;由拉格朗日乘数法可得,使式(5)达到最小值的条件如下:

FCM算法是一个简单迭代的过程,在批处理过程中,由上述两个必要条件,通过简单迭代更新及确定聚类中心C和隶属度矩阵U。
IFCM是基于直觉模糊集(intuitionistic fuzzy sets,IFS)理论的传统模糊C均值(FCM)的优化[9]。把只考虑隶属度的经典FCM推广为同时考虑真隶属度、假隶属度和犹豫度这3方面信息的直觉模糊集,同时引入一个新的参数——直觉模糊熵(intuitionistic fuzzy entropy,IFE)。相比经典FCM,使用直觉模糊集定义的模糊聚类可以收敛到一个更理想的聚类中心。
在IFCM中假设含有n个像素点样本的数据集A={A1,A2,…,An},其中每个样本都有m个特征,即Aj=(Aj1,Aj2,…,Ajn),并且Ajk=(tjk,fjk)(1≤j≤n,1≤k≤m),则n个待分类像素的样本的特征矩阵即为A=(Ajk)n×m,将像素点分为c类(2≤c≤n),设c个聚类中心为V={V1,V2,…,Vc},且Vi=(Vi1,Vi2,…,Vim),Vik=),则c个聚类中心的特征矩阵为V=(Vik)c×ms,像素点Aj与聚类中心Vi的距离为;模糊分类认为所有被分类的对象分别以不同的隶属度隶属于某一类,因此每一分类都对应一个模糊矩阵,而直觉模糊分类用直觉模糊值表示隶属程度,则每一分类对应一个直觉模糊矩阵R,即R=(rij)c×n,其中rij=表示像素点Aj对第i类的隶属程度,且分别为像素点Aj对第i类的隶属度、非隶属度以及犹豫度。将由R中所有隶属度构成的矩阵记为μ,所有非隶属度构成的矩阵记为α,所有犹豫度构成的矩阵记为π。
聚类中引入了一个新的概念:直觉模糊熵(IFE)。本来这个概念是用来度量模糊集的模糊度的,Zadeh在1969年第一次使用了这个概念[10]。后来Kaufmann用测得的距离来重新定义了这个概念[11]。Yager把它定义为到一个聚类的距离以及它的补[12]。Szmidt和Kacpryzk从非概率的角度定义了熵[13]。直觉模糊熵给出了模糊集A的模糊程度,记为IFE(A),如式(8):
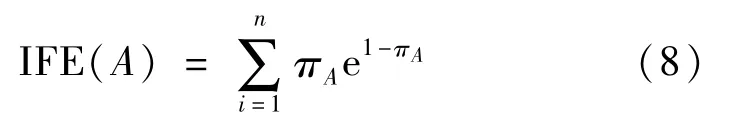
在FCM算法中价值函数为式(5),在IFCM算法中,为了使聚类中有效数据点最大化,使数据矩阵的熵最小化,引入了第二个公式,如式(9):

在此基础上引入结构函数R,通过结构函数R对隶属度矩阵μ2重新定义;首先构造一个卷积核对图像进行卷计算待分类像素点附近所有隶属度函数总和,得到卷积矩阵H,设N=μp×Hq(p,q为决定原有隶属度函数和结构函数相关性参数),对N每行元素求和后得到矩阵t,则重新定义的隶属度矩阵μ2的表达式如下:
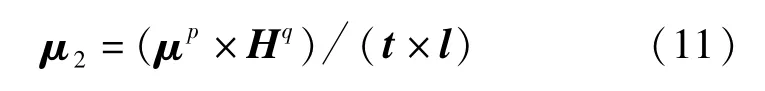
当p值一定时,q值越大聚类分割的效果越理想,因为q值越大相当于增加了像素空间特征的比重,但是q值若过大会导致聚类分割后细节处变模糊。结构函数不会对同类像素点的划分产生影响,对于噪声像素点式(11)考虑了像素间的结构特征,大大减少了噪声像素点的隶属度权重,从而对其加以抑制,可以有效避免错分情况的出现。
设将所有像素点分为n类,式中l为1行n列的行向量,则RIFCM_HSV方法的目标函数如式(12)所示:

RIFCM_HSV方法的基本步骤如下:
步骤1:获得待分割图片像素信息,转换到HSV色彩空间同时提取H分量。
步骤3:根据式(6)更新聚类中心,根据式(7),式(11)更新隶属度矩阵。
步骤4:根据式(12)计算价值函数。如果它小于设定阈值,或它相对上次价值函数质的改变量小于设定阈值,则依据最大隶属度准则对图像进行分割。否则返回步骤3。
算法流程图如图1所示。

图1 RIFCM_HSV算法流程图Fig.1 The flowchart of RIFCM_HSV algorithm
3 实验结果对比分析
3.1 颜色特征分析与选择
HSV空间中V分量受光照的影响最大,H分量基本不受阴影或过高亮度的影响,在HSV空间中对彩色物体进行检测效果会比在RGB颜色空间中更为可靠。实验环境设置为黑色背景加自然光环境,黑色背景在颜色上与目标区域存在较大差别[14]。图2为在数据集中随机选取一幅图像,提取其RGB空间和HSV空间各分量,通过三色线剖分析[15],如图2所示,图中第一行由左至右分别为R、G、B三个分量的图像,第二行分别为H、S、V三个分量的图像。

图2 RGB空间和HSV空间对比Fig.2 Comparison of RGB space and HSV space
通过图2可以直观感受到在HSV空间的H分量中背景区域和目标区域的区分度更高。再对图2中的各分量图像像素点的像素值分布情况进行对比分析,如图3所示,通过观察各个分量中像素值的分布,可见图3中第二行第一幅图H分量的像素值分布呈现两极分化的情况最为明显,更加有利于对图像进行聚类分割,所以HSV空间的H分量更适合用来做图像的聚类分割。

图3 各分量的像素值分布Fig.3 The distribution of pixel values of each component
3.2 聚类分割检测的结果与分析
利用此文提出的方法和OTSU法、K_means方法、FCM方法以及IFCM方法分别对在数据集中随机选取的猪肉图片进行聚类分割,对比检测出的目标区域的情况。K_means方法对HSV空间中每个分量的分割情况如图4所示。

图4 K_means分割结果Fig.4 The result of the K_means method segmentation
观察图4发现K_means方法对H分量分割的效果非常不理想,基本未识别到理想的目标区域,对S分量和V分量的分割识别到了大部分目标区域,但是由于自然光照射使猪肉表面形成了阴影,导致部分区域被识别为背景。
FCM方法对HSV空间中每个分量的分割情况如图5所示。观察图5发现FCM方法对H分量的分割效果优于K_means方法,但是FCM方法对噪声较为敏感[16],观察图5中的FCM_H可发现目标区域内部出现很多由于噪声导致的错分区域;对于S和H两个分量的分割效果和K_means方法的分割效果基本一致,同样由于自然环境下光照不均匀导致目标区域识别不全。

图5 FCM分割结果Fig.5 The result of the FCM method segmentation
RIFCM_HSV方法对HSV空间中每个分量的分割情况如图6所示。可以看到RIFCM_HSV方法对HSV空间中H分量的分割效果最为理想,目标区域内部的噪声对目标区域的检测影响不大;在文中所述几种方法中,RIFCM_HSV方法的效果最为理想。

图6 RIFCM_HSV分割结果Fig.6 The result of the RIFCM_HSV method segmentation
接下来通过人为向图像中添加噪声,测试RIFCM_HSV方法和FCM方法以及传统OTSU法的抗噪声能力。测试结果如图7、图8所示。图7为对原始图像加入噪声后进行Otsu阈值分割的结果,图8为对H分量图像分别加入0.1和0.2椒盐噪声后进行FCM分割和RIFCM_HSV分割结果对比。

图7 抗噪能力对比图(Otsu)Fig.7 A comparison of the ability to resist noise(Otsu)
如图7所示,当采用传统的Otsu法对自然光照环境下采集的猪肉图像进行分割时,由于光照环不均匀产生的阴影会使分割精确度降低,当在图像中人为加入噪声后,分割精确度又有明显的下降,使算法无法准确的分割出目标区域和背景区域,由此可见,传统Otsu法无法应对实际环境中的各种图像噪声。
如图8所示,当人为加入0.1和0.2的椒盐噪声后,FCM 方法检测出的目标区域相对于图5的FCM_h差距很大,而RIFCM_HSV方法检测出的目标区域与图6中的RIFCM_HSV_H检测出的目标区域相比,仅在目标与边缘产生错分现象,目标区域的主体部分基本保持一致。这主要是由于在选取基本不受阴影或过高亮度影响的H分量的同时,考虑了图像像素的结构和灰度信息,使聚类性能提高,对图像噪声的适应能力有了进一步增强,总体上获得了更理想的聚类效果。

图8 抗噪能力对比图(RIFCM_HSV和FCM)Fig.8 A comparison of the ability to resist noise(RIFCM_HSV and FCM)
表1以手工勾画的目标区域为标准,随机选取了9张猪肉图像进行9组分割检测试验,对FCM方法和RIFCM_HSV方法的分割效果进行定量评价。其中错分像素数、错分率定义如下:

将手工勾画的图像进行二值化处理后,变为二维矩阵,分割检测的结果图像同样是二维矩阵,将两个矩阵进行差值计算后,利用matlab统计差值计算后矩阵像素值的分布情况,即可获得错分像素数;得到错分像素数后,通过matlab对手工勾画的标准图像进行像素统计,得到标记出的目标区域的像素总数,错分像素数与目标区域像素总数的比值即为错分率。
在对取自自然光照环境中的猪肉图像进行分割时,相对于传统聚类分割方法,此方法在正常采集的图像上和人工添加了噪声的图像上的分割效果均优于传统方法,错分率均低于传统方法。
在表1的9组实验中,对正常采集的图像进行处理时,RIFCM_HSV方法的错分率平均低于传统FCM方法1.46%;在对人工加入了0.1椒盐噪声的图像处理时,相对于处理正常采集的图像,传统FCM方法错误率平均升高了16.15%,而RIFCM_HSV方法分割的平均错误率仅升高了1.57%;在对加入了0.2椒盐噪声的图像处理时,相对于处理正常采集的图像,传统FCM方法错误率平均升高了38.28%,而RIFCM_HSV方法分割的平均错误率仅升高了1.49%。

表1 错分率对比表Tab.1 Image segmentation error rate comparison table (%)
4 结论
结合HSV色彩空间的H分量相对于传统的RGB空间基本不受阴影或过高亮度影响的优势,提出了基于HSV空间的结构直觉模糊C均值聚类图像分割的方法,在传统的聚类图像分割方法的基础上引入了结构函数,在确定图像像素模糊隶属度过程中,考虑了图像像素的结构信息,增大了不同类别像素点间特征的区分度,通过聚类划分,将像素点分割为目标区域和背景区域两部分。通过数据对比可以得知,在对正常采集的猪肉图像进行分割时,RIFCM_HSV方法的效果略优于传统方法,当图像中噪声数量增高后,RIFCM_HSV方法的抗噪声能力优于传统FCM方法,与传统的FCM方法相比,RIFCM_HSV方法对噪声的鲁棒性更好,出现错误分割的几率更低,减少了图像预处理阶段的信息丢失,所以认为RIFCM_HSV方法更加适用于对实际环境中采集的图像进行分割预处理,为畜肉分级的前期图像预处理工作奠定了良好基础。
