热电材料塞贝克系数的不确定度评定

李 硕，郭 涛，姚雅萱，任玲玲

（1.中国计量科学研究院 前沿计量科学中心，北京 100029；2.北京科技大学 材料科学与工程学院，北京 100083）

1 引言

热电材料（thermoelectric materials，TE）又名温差电材料，是一类可以将热能和电能直接相互转化的新型功能材料，在计算机、航天和微电子技术领域的温差发电和制冷应用方面引起了人们的广泛兴趣［1～5］。

塞贝克系数是评价热电材料性能的关键参数。针对热电材料塞贝克系数的计量技术研究，美国国家标准与技术研究院（NIST）已研制出低温塞贝克系数标准物质碲化铋Bi2Te3（SRM 3451），相对扩展不确定度≤2.3%（k＝2），温度范围10～391 K［6，7］；德国联邦物理技术研究院（PTB）已研制出2种低温塞贝克系数标准物质ISOTAN和碲化铅PbTe，不确定度为2.5%～8%，温度范围300～850 K；英国国家物理实验室（NPL）也在研究纳米结构热电材料性能的测试方法；其他国家计量院也在研究塞贝克系数测量装置的溯源技术和相关标准物质。然而，由于测试仪器和方法的差异，目前热电材料塞贝克系数的测量结果相差较大，缺少统一性和规范性，常给热电材料的性能评价带来不确定性。

我国热电材料产业发展迅速，预计年产值近10亿元，但目前尚无相关计量标准装置和标准物质。为了准确提供量值传递服务，亟待开展热电材料塞贝克系数的计量技术研究工作。本文对塞贝克系数测量仪器的溯源性和准确测量方法进行了研究，并对塞贝克系数测量的各不确定度分量进行了评定。

2 塞贝克系数的准确测量

2.1 塞贝克系数的准确测量方法

塞贝克系数定义式为：

式中：S为塞贝克系数；ΔV表示两结点间的塞贝克电动势；ΔT表示两结点的温差，ΔT＝T2－T1，T1为冷端温度，T2为热端温度。温度梯度方向与电动势方向相同，S系数为正；反之，S系数为负。

准确测量方法：铜制样品台夹住样品两端，与之充分接触，水平放置于密闭加热炉内，炉腔内充填高纯氦气；炉腔温度升高至一定温度且样品两端温差小于1 K，热端样品台内置的微型加热器开始缓慢加热，与冷端样品台的温差逐渐加大；2支K型裸丝热电偶经导电银浆分别焊接于样品同面固定两结点，测量样品热端和冷端温度，K偶的正极收集两结点相应的塞贝克电压，热电偶外接同步数据采集卡，同时采集样品冷热端温度和塞贝克电压；每个被测温度点，取温差1～3 K的相应塞贝克电压数据，“斜率法”拟合计算得到塞贝克系数［8～12］。塞贝克系数测量系统见图1所示。

图1 塞贝克系数测量系统Fig.1 Seebeck coefficient test system

2.2 塞贝克系数准确测量方法的验证

采用NIST的低温塞贝克系数标准物质碲化铋Bi2Te3（SRM 3451）对上述建立的塞贝克系数测量方法进行验证，重复测量5次。图2为验证结果，由图2可见：已建立测量方法的塞贝克系数测量结果在标准物质的不确定度范围内，且与标称值较为接近，验证了测量方法的准确性和有效性。

图2 塞贝克系数测量方法验证结果Fig.2 The Seebeck coefficient test method validation

2.3 塞贝克系数测量系统的溯源性

根据定义式（1）可知，需将塞贝克系数分别溯源至温度和电压，即将K型热电偶和同步数据采集卡分别进行溯源。溯源路径见图3所示，由电压V＝I·R，电流I和电阻R分别溯源至数字多用表检定装置和直流电阻副基准装置；温度溯源至温度国家基准装置。

图3 塞贝克系数溯源路径Fig.3 The traceable path of Seebeck coefficient

3 塞贝克系数的测量不确定度评定

以P型碲化铋Bi2Te3块体热电材料作为测量对象，对冷端温度、热端温度和塞贝克电压测量值进行校准，得到塞贝克系数校准值，并对所得量值进行A类不确定度和B类不确定度评定［13，14］。

3.1 A类不确定度评定

A类不确定度uA即测量过程引入的不确定度，包括测量重复性所得标准偏差和塞贝克系数拟合的标准偏差。

采用建立的塞贝克系数准确测量方法重复测量12次，取算数平均值为塞贝克系数测量值。测量重复性所得标准偏差可由贝塞尔公式计算［15］：

塞贝克系数拟合的标准偏差uA2，即拟合直线y＝a＋bx斜率b的标准偏差：

其中，相关系数r为：

则A类不确定度uA

3.2 B类不确定度评定

B类不确定度uB即测量装置引入的不确定度，包括温差测量引入的不确定度分量uB-ΔT和塞贝克电压测量引入的不确定度分量uB-ΔV，各不确定度分量见图4所示。

图4 塞贝克系数测量的B类不确定度Fig.4 The type-B measurement uncertainty of Seebeck coefficient

塞贝克系数的测量模型见公式（1），由于温差ΔT和塞贝克电压ΔV测量无相关性，故不确定度uB可表示为：

将塞贝克系数测量模型作对数变换，采用相对不确定度可表示为：

3.2.1 温差ΔT测量引入的不确定度uB-ΔT

温差ΔT的测量模型

根据塞贝克系数的测量原理，冷端温度T1和热端温度T2测量存在相关性，可得温差ΔT测量引入的不确定度uB-ΔT为：

冷端温度T1和热端温度T2同时测量，相关系数r为

式中s（x）和s（y）分别为x和y的标准偏差。则

图5 热电偶温度校准直线Fig.5 The temperature calibration line of thermocouple

式中：S′为剩余标准偏差；a为校准直线截距；b为校准直线斜率；p为测量次数（p＝1）；n为温度校准总次数；SXX为温度标准值与温度标准值的平均值之差的平方和；Tm为待校准温度值；TAM为温度标准值的平均值；TM，j为温度测量值；TC，j为温度标准值。

参照GB／T 16839.1-2018 《热电偶》第1部分：电动势规范和允差，K型热电偶的温度（T）-电动势（E）反函数关系式［16］：

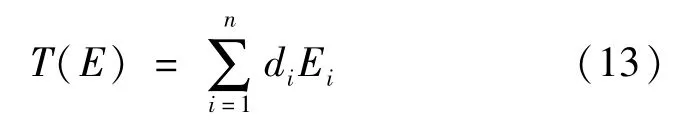
式中：E为电动势；T为温度；di为多项式第i项的系数；n为多项式阶数。

则灵敏系数为

图6 冷端温度电动势校准直线Fig.6 The voltage calibration line of cold end temperature

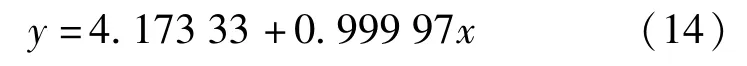
式中：x为电动势标准值；y为电动势测量值。相关系数R2＝1。

式中：S′为剩余标准偏差；a为校准直线截距；b为校准直线斜率；p为测量次数（p＝1）；n为电压校准总次数；SXX为电压标准值与电压标准值的平均值之差的平方和；Vm为待校准电压值；VAM为电压标准值的平均值；VM，j为电压测量值；VC，j为电压标准值。

则灵敏系数为

因此，冷端温度T1测量引入的不确定度为：

因此，由温差ΔT测量引入的不确定度uB-ΔT为：

3.2.2 塞贝克电压测量引入的不确定度分量uB-ΔV

塞贝克电压测量引入的不确定度uB-ΔV，包括电压校准直线引入的不确定度uB-ΔV-CL和采集卡通道电压校准的不确定度uB-ΔV-CR。

（1）电压校准直线引入的不确定度uB-ΔV-CL

以同步数据采集装置校准证书中对应数据采集通道的电动势标准值为x轴，测量值为y轴，线性拟合校准直线见图7，直线函数关系式为：

图7 塞贝克电压校准直线Fig.7 The Seebeck voltage calibration line

式中：x为电动势标准值；y为电动势测量值；相关系数R2＝1。

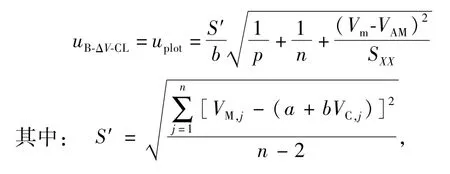
式中：S′为剩余标准偏差；a为校准直线截距；b为校准直线斜率；p为测量次数（p＝1）；n为电压校准总次数；SXX为电压标准值与电压标准值的平均值之差的平方和；Vm为待校准电压值；VAM为电压标准值的平均值；VM，j为电压测量值；VC，j为电压标准值。

取uplot最大值作为不确定度uB-ΔV-CL：

（2）采集卡通道电压校准的不确定度uB-ΔV-CR

则塞贝克电压测量引入的不确定度uB-ΔV

B类不确定度uB采用相对不确定度表示：

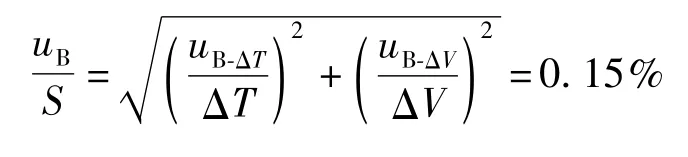
则温度点296.48 K下，B类不确定度uB为：

3.3 合成不确定度uc和扩展不确定度U

塞贝克系数测量的合成不确定度uc可表示为：

取包含因子k＝2，扩展不确定度U为：

表1为塞贝克系数测量不确定度评定结果。

表1 塞贝克系数测量不确定度评定结果Tab.1 Uncertainty evaluation results of Seebeck coefficient

4 结论

（1）基于测量模型，将塞贝克系数分别溯源至温度和电压，建立了塞贝克系数的溯源路径；

（2）通过标准物质验证了塞贝克系数测量方法的准确性；

（3）对塞贝克系数测量不确定度进行了评定，相对扩展不确定度为0.46%～2.52%（k＝2）。