高线性度的二维无耦合纳米压电位移系统设计

罗四维，乐燕芬，彭 洋，吴俊杰，雷李华，张 波，金 涛

（1.上海理工大学 光电信息与计算机工程学院，上海 200093；2.上海计量测试技术研究院，上海 201203）

1 引言

随着科学技术的发展，微电子工程、光学精密工程、计量科学与技术等领域对纳米位移技术的要求越来越严格，不但要求具有纳米级位移精度，还需要有较高的灵敏度且易于控制［1，2］。现阶段的纳米位移系统通常采用压电陶瓷作为驱动元件，压电陶瓷由于具有良好的动态特性和高分辨率等特点，已成为微位移驱动方面的理想器件［3，4］。但在使用过程中也存在一些缺陷，如存在非线性、蠕变、机械振动和热漂移问题［5］。

为了在压电致动器上获得高度线性化的位移操作，有关学者提出了许多可行的方法及措施。反馈控制是工业领域中应用最广泛的方法，代表性的方法有比例积分微分控制（PID）［6］、比例二重积分控制（PII）［7］及比例积分控制（PI）。然而，这些控制方法均需要高精度位移传感器，但传感器的噪声会限制控制与位移的精度［8］。前馈控制是另一种有效的方法，主要思想是首先获得描述驱动器的滞后行为的数学模型，然后基于所提出的模型的反演来实现前馈控制器。前馈控制虽然不涉及传感器，但是模型的不确定性通常将定位精度限制在驱动范围的1%～3%［9，10］。它的复杂性限制了可实现的精度和实际应用。电荷控制是除反馈和前馈控制外的另一种控制方案，其控制原理是由于压电陶瓷的位移与电荷量成正比，所以可以简单的通过电荷反馈来控制压电陶瓷的位移，既不需要昂贵的位移传感器也不必建立复杂的数学模型就可以大大改善压电陶瓷的迟滞。在开环控制的纳米定位系统中，电荷控制器被广泛应用。

传统电荷控制器长期存在的问题是有限的低频性能以及没有接地配置的功能，而且其存在的剩余迟滞问题也阻碍了电荷控制器去获得更高的位移线性度。为了应对这一挑战，Fleming A J等［11］提出了一种具有接地配置的电荷控制器。但该方法需要一块高性能的差分放大器而且它的低频性能并没有得到明显的改善；之后，Fleming A J［12］又提出了一种具有有源直流稳定性的电荷控制器，解决了有限的低频性能的问题，但这也使得压电陶瓷没有了接地配置的功能。

前面提到的这些方法大部分是用于单个压电致动器的高线性操作的，而对于多个压电致动器的同步高线性操作并不适用，但是使用多个压电致动器驱动的优点是很明显的。首先，多个压电致动器的同步运行可以实现推力的成倍增加。其次，可以实现大尺寸器件的高精度位置控制，这种需求常常出现在大尺寸光学元件上。微位移平台作为位移系统的另一个核心部分，其结构设计、刚度、位移行程及是否存在运动方向上的互相干扰即耦合误差［13］对整个系统的精密程度也起到了重要的作用［14，15］。

本文的压电位移系统设计了一种具有接地配置功能的压电控制器，通过非线性反馈控制和相似控制相结合的方法［16］来改善压电致动器的位移轨迹线性度和无法接地配置的问题，进一步提高了位移线性度。为显示控制效果，还设计了一种内外层嵌套式串联结构二维压电微位移台，相比于叠加式结构其运动惯性较小，对驱动控制部分的要求较并联结构更低，且柔性铰链平行布置实现位移解耦，有效地避免了运动方向上的相互干扰。本系统的验证实验部分搭建了激光干涉测量系统，实现了运动方向上的解耦，且行程及位移线性度达到了设计要求。

2 压电控制器的设计

2.1 传统电荷控制器的原理

电荷控制器的原理通常如图1所示。假设压电陶瓷是一个理想的电容Cp，运算放大器也看作理想的，Rf和R1为无穷大阻值的电阻，实际经过压电陶瓷的电荷量可以写为：

图1 电荷控制器的基本原理图Fig.1 Schematic diagram of a charge controller

式中：Qact是实际通过压电致动器Cp的电荷量；C1为电荷控制器的输入电容；Vin为输入电压；Vout是输出电压。

如果Vin和Qact是线性变化的，那么相对应的位移变化也是线性的，为了防止低频漂移，可以在C1和Cp上分别并联电阻R1和Rf。其传递函数可以写为

从传递函数中可以看出该电路中有一个零点s＝－1／R1C1和一个极点s＝－1／RfCp。为了尽量减少零点和极点对增益的影响，令R1C1＝RfCp，实际应用中的输入信号频率尽量远离零点和极点。这样输入电压和输出电压的关系为

由于Cp在实际中并不是定值，因此输出电压Vout与Vin并不是完全线性相关的。这种传统的电荷控制方法虽然可以一定程度上降低压电致动器的迟滞导致的轨迹非线性偏差，但是却存在过补偿现象。另外，通过图1可以看到压电陶瓷的Cp的一端接的浮地，在一些场合下压电陶瓷必须有接地配置［17］，而这也使得经过压电陶瓷的电荷需要先经过前置低压放大器，这并不利于大推力的压电致动器。另外，由于该电路存在的极点和零点在低频处，这导致当输入信号的频率低于极点或零点频率时，电荷控制器会转变成电压控制器。因此这种电路结构的电荷控制器并不适合低频和静态操作。

2.2 多压电致动器的电荷控制器的设计

本文在传统电荷控制器的输出端通过外接一个同型号的压电致动器至地，从而构成一种含有两个压电致动器的电荷控制器，图2是该种控制器的基本结构原理。A1为前置放大器的增益，实验中设定A1＝－1；HVA为高压放大器。

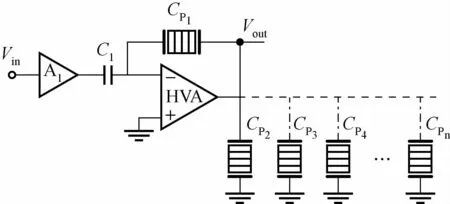
图2 同步操作的多压电致动器的电荷控制器原理图Fig.2 Schematic diagram of charge controller for multi-piezoelectric actuator operated synchronously

假设这些压电致动器的电容是近似相等，即：

假设运放是理想的，则这些执行器上的电荷也是近似相等的，即：

由式（1）可得理想情况下Qp与输入电压Vin是线性的关系，那么根据上式可得Qp1，Qp3，Qp4，…，Qpn等也有线性的关系。这意味着当图2中的Cp1的位移是线性的时候，同时也将在Cp2上获得线性的位移。理想情况下可以外接无数个同型号的致动器，但考虑到控制器的相位滞后以及运放驱动功率的问题，实际使用中外接的同型号控制器的数量不能过多。为了进一步降低传统电荷控制方法的过补偿导致的轨迹非线性以及电荷控制器在低频和静态情况下不适用的问题，结合上面的多压电制动器的电荷控制，提出了一种具有非线性反馈网络的多压电陶瓷的电荷控制方案（为了叙述方便这里仅外接一个压电致动器）。

假定其中带有迟滞行为的压电陶瓷可以等效为一个可变电容Cp，其电容变化为δCp；A1为反相跟随放大器；A2为高压放大器，A2的值与电荷放大器的增益互为倒数；A3为可调放大器，补偿因子A3值为正数；A4为误差放大器；R1和Rf为电荷控制器提供直流反馈路径。具有非线性反馈网络的双压电陶瓷的电荷控制器如图3所示。

图3 具有非线性反馈网络的双压电陶瓷的电荷控制器Fig.3 A charge controller for piezoelectric bimorph with nonlinear feedback network

实际经过压电致动器Cp的电荷为

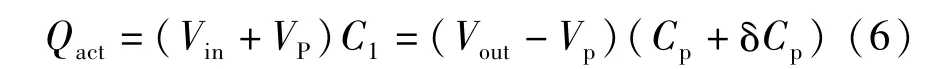
式中Vp是Vout非线性偏差的尺度。

由于Vout≫Vp，因此有：

其中，

可以得到：

通过比较式（3）和（11），可以看出增益A3实际上影响了控制器的输出Vout的非线性，当增益A3＞0时，可以起到校正过补偿和欠补偿的效果。另外，在式（11）中，由于Vp≪Vout，忽略了Vp的作用。如果考虑Vp，则Vp和Vout的关系式为

考虑到迟滞等效的电容对于电荷控制器的位移非线性的影响［17］，将Cp1写为Cp1＋δCp1，Cp2写为Cp2＋δCp2可得Cp2两端的电压为：

考虑到非线性环中A2和A3的影响，由式（11）可得压电致动器Piezo2上的电荷表达式如下：

从式（14）可知piezo2的电荷不仅可以通过Vin来控制，而且也与A3的值有关。另外，压电致动器piezo1和piezo2的相似度也会影响最终的控制器效果，尤其是压电致动器piezo1和piezo2的电容是否相等。本系统选择的压电陶瓷的静态电容值均以LRC电桥仪测得的数据为准。如果再外接致动器在该控制器上，那么它们和piezo2是等价的。如果只将piezo2作为实际压电陶瓷而piezo1仅用于反馈，那么piezo2会具有真正的接地配置。当具有接地配置的高压放大器驱动的是一个电容和压电陶瓷的组合体时，此时实际压电致动器的驱动功率将会受到串联电容的影响，而多个压电致动器的电荷控制器的方案中并不需要担心这一点。配置低频漂移最简单的方法是在反馈电容和输入电容上并联电阻，但是这会在电路的低频处产生零点和极点。为了尽可能减小零点和极点对于电路的影响，应该使得零点和极点尽可能相等而且工作频率尽可能远离零点和极点。本文将直流反馈路径的放大倍数设置为20倍，采用T型电阻网路作为反馈电阻，不仅可以得到大阻值电阻，还可以减小单一大阻值电阻带来的噪声，这可以大大改善传统电荷控制器的低频性能，T型电阻网络的电阻等效公式为：

式中：Rf1＝Rf2＝110 kΩ；Rf3＝676Ω。

图4为控制器的电路原理图，高压放大器HVA采用高输入阻抗、高电压转换速率的APEX PA85A器件；可调增益A3由20 kΩ定值电阻和一个线性数字电位器组成（红色圆圈）。因此，A3可以调整到最大值0.05，最小值可以调整到0。在实验中，piezo2通过调整A3的值而具有最小的位移轨迹偏差。当A3设置为0时，非线性反馈回路被禁用。压电致动器1直接安装在控制板上，致动器2通过屏蔽电缆连接到控制板上。

图4 控制器电路原理图Fig.4 Circuit schematic of the controller

HVA采用高输入阻抗、高电压转换速率的APEX PA85A器件；可调增益A3由20 kΩ定值电阻和一个线性数字电位器组成（红色圆圈）。因此，A3可以调整到最大值0.05，最小值可以调整到0。在实验中，piezo2通过调整A3的值而具有最小的位移轨迹偏差。当A3设置为0时，非线性反馈回路被禁用。压电致动器1直接安装在控制板上，致动器2通过屏蔽电缆连接到控制板上。

3 位移台结构设计及有限元仿真分析

3.1 位移台结构设计与刚度计算

图5为二维压电微位移平台结构模型图及柔性铰链几何示意图，平台采用了S型柔性铰链作为导向机构，压电陶瓷作为驱动元件。位移台两个自由度方向均采用平行对称结构布置，每个柔性铰链的两端分别与中间的承载运动平台和位移台外框固定，结构上将Y轴方向的运动结构嵌套在X轴方向的运动结构内，压电致动器放置在位移平台的中间卡槽内。在压电陶瓷驱动力作用下，引起S型柔性铰链发生变形，实现二维微动平台的位移输出。

图5 压电位移平台结构模型图及柔性铰链几何示意图Fig.5 Structure model of piezoelectric displacement table and the geometry diagram of a flexure hinge

压电位移台的刚度性能以及输出位移是由柔性铰链决定的，因此，对柔性铰链进行理论计算和分析是十分重要的［18］，由于位移台中柔性铰链是对称布置，且形状及受力情况相似，因此只对一个铰链进行分析。根据柔性铰链在位移台中的受力情况，将柔性铰链简化为一端固定、另一端受力F作用的悬臂梁，得到它受力方向上的刚度计算公式。设置图5中柔性铰链的结构参数：长度L、宽度W、高H、铰链间宽D。

在所用弹性材料服从胡克定律的条件下，悬臂梁上的某一段受到的力引起的形变，不会对其他段产生影响，所以若想得知柔性机构受力产生的整体形变，可以将其分为5部分，然后依次将各个分段的形变相加，就可得到悬臂梁的整体形变。将柔性铰链简化为如图8所示悬臂梁结构，并分段标记为A、B、C、D、E段5个部分，使用分段计算法得到悬臂梁左端下面①点受力载荷的总位移S（1）几何关系，可得此悬臂梁在力载荷F作用下的位移形变图见图6。

图6 柔性铰链整体位移形变图Fig.6 Flexure hinge overall displacement diagram

图6中，端面扭转角度θ＝－（FL2）／（2EI），当A段单独形变时，设S为水平最大位移，其计算公式为

根据材料力学中的伪刚体法，分别计算每一段梁的形变对柔性铰链整体位移的影响，最后以此将产生的形变代数相加，即可得到在载荷力F的作用下图6中①点的总位移S（1）：

式中：I为惯性矩，I＝（HW）3／12；E为弹性模量；D为柔性铰链横截面积，P＝HW；代入式（17）可得柔性铰链①点在受到力载荷的作用下的位移公式：

再根据力学弹性理论中的胡克定律F＝k·Δx可知在材料的线弹性范围内，固体的单向拉伸变形与所受的外力成正比，柔性铰链的刚度系数表达式为

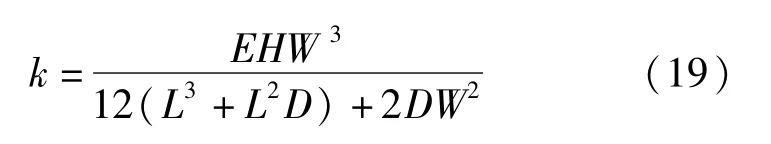
由于同一方向有两个柔性铰链并排放置，刚度也增加一倍。由式（19）可知刚度系数k是与设置的柔性铰链结构参数，L、W、H、D相关的函数。根据此柔性铰链在压电位移台中的具体要求，还有位移台需要达到的刚度和位移需要，以及铰链几何参数与平台输出位移关系。确定各参数具体数值，X方向：L＝20 mm、W＝1 mm、H＝10 mm、D＝2 mm；Y方向：L＝15 mm、W＝1 mm、H＝10 mm、D＝2 mm。位移台制作材料为45＃钢材料，其弹性模量E＝210 GPa，泊松比μ＝0.28，密度ρ＝7 850 kg／m3，许用应力σ＝340 MPa。

3.2 位移台有限元刚度分析及耦合位移仿真

通过初步设计得到的平行铰链的结构尺寸参数，本文应用ANSYS有限元分析软件对微动台的性能，包括刚度、行程、耦合位移进行有限元仿真分析，研究理论设计的合理性。根据设计的尺寸参数在Space Claim三维设计软件中构建微动台的三维模型，模型绘制以及网格划分后直接导入到ANSYS软件中的static structure组块中分析，在施加约束和载荷时，模拟微动台实际工作情形，将基座的4个螺纹安装孔端面进行固定限定其自由度，然后对微动台工作台施加力载荷，通过查看工作台位移输出仿真结果，来计算其刚度。图7为位移台X、Y运动方向模拟刚度及位移分析云图。

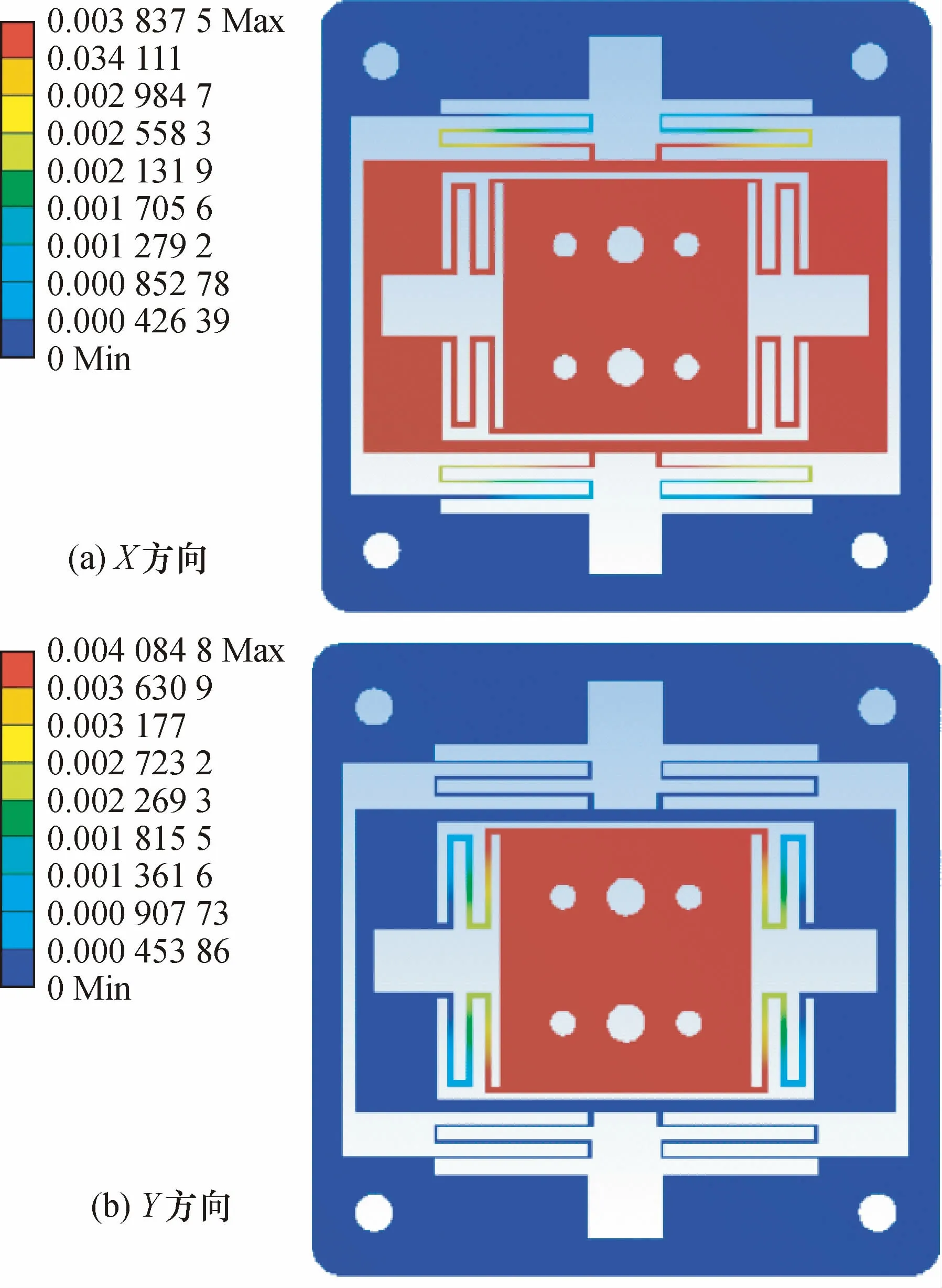
图7 位移台X、Y运动方向模拟刚度及位移分析云图Fig.7 The simulated stiffness and displacement of displacement platform X and Y was analyzed

理论计算X方向刚度值大约为7.954 2 N／μm，而微动台需实现3.8μm位移行程，故仿真时对载荷施加面施加约30.23 N的力载荷。同理在Y方向施加约69.54 N的力载荷。仿真分析结果显示，在工作台X方向受到30.23 N的力载荷时产生了大约3.83μm的位移量，Y方向位移量为0μm；Y方向受到69.54 N的力载荷时产生了大约4.08μm的位移量，X方向位移量为0μm。故可计算通过有限元方法得到的微动台X方向刚度为7.89 N／μm，Y方向刚度为17.04 N／μm，位移理论值与仿真结果偏差在0.3%左右，接近理论值。且仿真结果显示当只对位移台单一运动方向施加力载荷时，位移台仅在受力方向有位移产生，在另一运动方向没有位移产生。说明此位移平台结构可以实现在X，Y方向运动无耦合。验证了理论分析可靠性，故符合设计要求。理论计算与仿真刚度产生偏差的原因是平台的理论分析采用伪刚体模型法，根据力学理论建模时进行了一定简化。

4 高线性度的压电位移系统测试实验

4.1 测试条件与仪器

实验基于雷尼绍XL-80型干涉装置，建了一套激光干涉纳米测量系统，其框图如图8所示。

图8 激光干涉纳米测量系统框图Fig.8 Block diagram of laser interferometer nanometer measurement system

该干涉系统具有环境补偿功能可以对气压、湿度和温度进行实时采集，并对测量结果进行实时修正，干涉仪测量分辨率可以达到1 nm。

实验中压电陶瓷推动着直角棱镜做水平的直线运动，而另一块直角棱镜固定不动。两者之间产生的光程差随压电陶瓷的形变而改变，干涉仪将光程差信息处理后转化为位移信息并上传至计算机，由计算机上的相应上位机软件进行实时处理并显示位移信息。实验采用的压电陶瓷为NECTOKIN公司生产AE0203D08F型叠堆压电陶瓷，其长为5.01 mm、宽为1.8 mm、高为2 mm。该压电陶瓷的参数性能指标见表1。

表1 压电陶瓷的参数性能指标Tab.1 Performance indicators of piezoelectric ceramics

实验装置如图9所示，它由信号源、压电陶瓷、光干涉测量3部分构成。为避免环境对于测量装置的干扰，本文将实验装置置于气浮平台上并在实验开始前对于整个装置预热2 h。

图9 实验环境及测量实物图Fig.9 Experimental environment and physical picture of measurement

4.2 实验结果分析

为了更好地说明压电致动器的位移轨迹偏差使用最大位移误差MTE（%）来描述，表达式为

式中：Ei是轨迹偏差；δD是压电致动器的移动量。

本文对比了加入T型电阻网络前和后的效果，见图10。控制器的转换频率从0.89 Hz降低为0.13 Hz。通过测试数据可以得出，该控制器具有良好的位移轨迹线性度。在频率为2 Hz三角波输入的情况下，X、Y方向的运动位移分别为3.892 m和3.995 m。将上述轨迹曲线与标准三角波曲线进行比较，可以得到轨迹的偏差。图11为X、Y运动方向的轨迹误差图。可以看到最大轨迹偏差仅为31 nm和38 nm，最大非线性偏差（MTE）分别仅为0.79%和0.95%，线性度分别提高65.3%和64.8%。表现出了良好的轨迹线性度。这说明非线性反馈网络对于多个压电陶瓷的同步操作的线性度提高也是有效的。

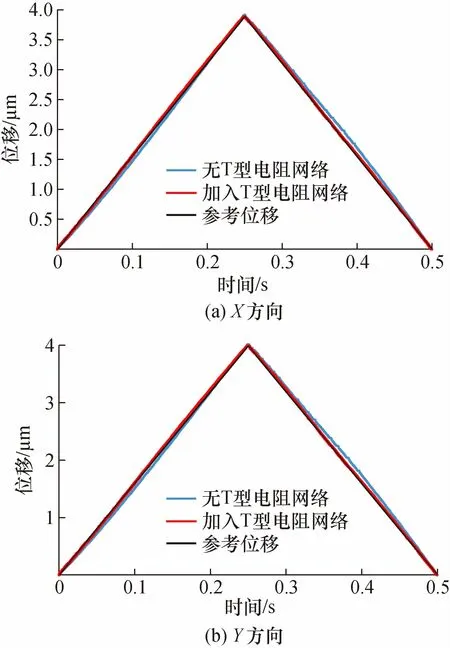
图10 微位移平台位移曲线图Fig.10 Displacement curve of micro displacement platform

图11 X、Y运动方向的轨迹误差图Fig.11 Trajectory error graph of X and Y direction of motion

两个压电致动器的轨迹一致性也是该控制方案的一个重要评价指标。本文实验了在相同幅值（幅值为4.5 V）而不同频率（0.5，1，2，5和10 Hz）的三角波的输入下控制器的带来的控制效果。以2 Hz信号X方向上的位移运动为例阐述实验具体过程，输入2 Hz三角波通过微调A3的值为0.007后，被控制的压电致动器（piezo1）具有了最小的位移偏差。然后保持A3不变再外接一个压电致动器（piezo2），其电容量Cp2为0.087μF。虽然它们的电容量差1 nF，但它们之间的轨迹偏差最大仅为9 nm（约为行程的0.23%），表现出了高度的一致性。piezo1、piezo2的最大轨迹误差分别为0.027μm、0.031μm（约为行程的0.69%、0.79%）最后微调A3的值为0.008后，piezo2的最大轨迹偏差为24 nm，MTE从0.79%减小到了0.61%。这说明非线性反馈网络对于多个压电陶瓷的同步操作的线性度的提高也是有效的，基于相似控制原理使得无反馈控制的压电致动器piezo2表现出了高线性度。图12显示了这一结果。

图12 X方向上两个压电致动器各自的位移误差Fig.12 Displacement error of two piezoelectric actuators in X direction

对比了加入T型电阻网络之前和之后的数据，控制器的转换频率从0.89 Hz降低为0.13 Hz。控制器在不同频率（低频段）下的控制效果显示在了图13中，可以看出由于两个压电致动器的差异导致位移轨迹的不完全重合，由于电路的转换频率为0.13 Hz，当靠近该频率时候非线性反馈环路的效果变差。此外，虽然两个压电致动器的差异使得它们的轨迹无法完全重合，但是却可以导致Piezo2的轨迹偏差进一步减小。实验中将A3补偿因子的值从0.007变为0.008，导致piezo2的位移线性度得到改善，图13结果（灰色标记点线）说明了这一点。这意味着，若仅将Piezo2作为实际致动器来用而piezo1不参与致动，相比于传统非线性电荷控制器其控制效果也会有所改善。

图13 几个低频率信号下的两个压电陶瓷各自的控制效果Fig.13 Control effect of two piezoelectric ceramics under several low frequency signals

为了测量位移平台的是否存在耦合位移，在X，Y运动方向施加驱动力，使平台产生位移，再在其正交方向使用激光干涉仪对可能出现的耦合位移进行测量，得到的压电位移平台的耦合曲线如图14所示，可以看出，耦合偏移误差分别仅为0.090%，0.098%证明此嵌套式串联结构可以有效地避免耦合位移。

图14 微位移平台运动耦合误差Fig.14 Coupling error of motion of micro-displacement platform

实验结果显示了多压电电荷控制器方案用在纳米位移操作上的优良性能。实测的结果与仿真和理论分析的结果存在一定的误差。其原因有两点：

1）微位移平台存在加工误差和压电陶瓷的安装误差；

2）理论分析建立在一定假设基础上，有限元网格划分以及数值解具有近似性。

5 结论

本文设计了一套高线性度的二维无耦合压电位移系统，在典型电荷控制器的基础上，提出了一种适用于多个压电作动器同步线性运行的电荷控制器。与传统的电荷控制器相比，它不仅实现了多个压电驱动器的同步线性运行，而且还提供了良好的接地配置实际的执行机构。设计了相应的二维串联嵌套微位移平台。该平台具有刚度对称、固有频率高且可消除耦合位移等特点。并通过实验测量了该控制方案的性能及可行性。实验结果表明：非线性反馈网络将压电陶瓷的轨迹误差减小到行程范围的0.79%，最小仅为0.69%。T型电阻器网络将控制器的转换频率降低到0.13 Hz而这仅仅是在一个88 nF电容量的压电致动器上实现的，说明电荷控制器的低频性能得到了较大改善。两个压电致动器之间轨迹偏差仅为行程范围的0.23%，与此同时它们各自的轨迹误差均不超过0.95%，表现出了良好的同步性和轨迹线性度。且两个运动方向的耦合位移误差分别仅为0.090%和0.098%，证实了该系统确实可以有效地避免二维运动的耦合问题，其性能指标基本满足光学精密仪器的需求，且控制方案易于实现，成本较低。为了进一步提高控制器的低频性能，未来工作重点将会增加有源直流稳压电路的研究。