基于线性变换球面分布的实时间接光泽反射
2023-02-21夏博刘艳丽曾威蒲一磊张严辞
夏博,刘艳丽,曾威,蒲一磊,张严辞
1. 四川大学计算机学院,成都 610065; 2. 四川大学视觉合成图形图像技术国家重点学科实验室,成都 610065
0 引 言
基于虚拟点光源(virtual point lights,VPLs)的立即辐射度算法(Keller,1997;Luksch 等,2019;Wang 等,2020)是一种常用的全局光照算法,通过借助大量虚拟点光源计算着色点的间接光照,优点是适用于动态场景,能够使用基于物理的光照模型进行光照计算,缺点是光照计算量较大,通常只能模拟一次反弹的间接光照。
反射阴影图算法(Dachsbacher和Stamminger,2005)可以快速生成虚拟点光源。该算法的提出加速了实时立即辐射度方法的发展,但是通常只能模拟间接光的漫反射效果。由于光泽反射相比于漫反射要复杂很多,使用立即辐射度方法实时渲染出比较真实的间接光泽反射效果一直是具有挑战性的难题。Dachsbacher和Stamminger(2006)基于反射阴影图,通过将虚拟点光源的光照信息溅射到相邻像素的方式,实时渲染出了间接光泽反射效果,但在计算间接光照时只用Phong模型,该光照模型不符合物理定律,无法渲染出真实效果。Tokuyoshi和Harada(2017)提出使用基于物理的GGX BRDF(bidirectional reflectance distribution function)计算每个虚拟点光源和着色点处的光泽反射GGX SLC(stochastic light culling)算法,虽然能得到相对真实的间接光泽反射效果,但是GGX BRDF公式极其复杂,计算开销太大,场景中虚拟点光源的数量将成为该算法的性能瓶颈。
为了降低GGX SLC算法渲染间接光泽反射效果时的计算开销,本文基于数学方法中的线性变换球面分布(Heitz 等,2016),将复杂的GGX BRDF拟合为另一种计算复杂度较低的球面分布,并在多点光源环境下提出了一种更高效的实时间接光泽反射渲染算法。
1 相关工作
用于快速生成虚拟点光源的反射阴影图方法提出后,大量研究投入到立即辐射度算法,如何高效利用虚拟点光源渲染全局光照一直是研究重点。
对虚拟点光源带来的多光源问题,Dachsbacher等人(2014)进行了详细介绍,其中对光源进行聚类是一种常用方法。Lightcuts(Walter 等,2005)就是对光源进行聚类的一种经典方法,使用二叉树组织光源,在着色时从树上选择一个lightcut对着色点进行光照计算。基于最原始的Lightcuts,该方法出现了一些变种,如多维的Lightcuts(Walter 等,2006)和双向的Lightcuts(Walter 等,2012)。通过对lightcut的选择引入随机性(Yuksel,2019;Lin 和 Yuksel,2020)解决了从光源树上采样的相关性问题。此外,还有结合重要性采样的方法(Vévoda 等,2018;Estevez和 Kulla,2018;Moreau 和 Clarberg,2019)以加速光照计算。另外,在实时渲染中交叉采样方法(Segovia 等,2006)可以减少每个像素着色时需要的虚拟点光源数量。
光源裁剪是另一类常用的多光源加速算法。Dachsbacher和Stamminger(2006)通过溅射虚拟点光源影响范围的边界几何来渲染焦散效果。Balestra(2008)提出对渲染窗口进行分块,每一个分块只需要对本分块有影响的光源进行着色计算。通过对深度方向上再次分块(Olsson 等,2012)可以进一步提高了分块着色的裁剪精度。尽管光源裁剪算法极大提高性能,但对光源影响范围的限制造成场景中着色时的黑暗性偏差。Tokuyoshi和Harada(2016)提出使用随机的光源范围进行裁剪来解决此问题。在计算光泽反射效果时,双向反射分布函数(BRDF)是非常重要的一部分。Cook和Torrance(1982)首次将基于微表面的BRDF引入计算机图形学。关于BRDF中最重要的法线分布函数有诸多研究。广泛使用的是Beckmann(Beckmann 和 Spizzichino,1987)、Phong(Phong,1975)和GGX(Walter 等,2007)等法线分布函数,但只有GGX分布具有较好的拖尾效应,因此GGX BRDF广泛应用于计算机图形学工业领域(McAuley 等,2012;Lagarde 和 de Rousiers,2014)。然而,完全基于物理的GGX BRDF计算非常复杂,在实际应用中需要用一些方法来加速光照计算。Tokuyoshi和Harada(2017)提出计算一个紧凑的椭球包围体来近似虚拟点光源的影响范围,并结合随机光源裁剪来产生光泽反射效果。Heitz等人(2016)提出使用线性变换球面分布这种数学思想来预计算GGX BRDF,从而避免了实时计算GGX BRDF的高开销问题。该方法由于在实时渲染中的出色表现,应用于多种渲染算法中(Li 等,2018;Diolatzis 等,2020;Luksch 等,2020)。
2 算法概述
立即辐射度算法的核心思想是使用大量虚拟点光源计算间接光照。即
(1)
式中,Lo是着色点p沿观察方向ωo的辐射亮度,N表示场景中虚拟点光源的总数,Ii(ωi)表示第i个虚拟点光源在ωi方向上的辐射强度,n是着色点的法线,f(p,ωi,ωo)是双向反射分布函数BRDF,〈·,·〉是向量点积运算。
为了用立即辐射度方法渲染出基于物理的间接光泽反射效果,GGX SLC算法使用GGX BRDF模型描述着色点以及虚拟点光源处表面的材质属性,即着色点的辐射亮度Lo和虚拟点光源的辐射强度Ii都需要通过GGX BRDF计算。然而,GGX BRDF公式极其复杂,当用于计算间接光泽反射时,光照计算的复杂度会随着场景中虚拟点光源的数量呈线性增加,最终会成为GGX SLC算法的瓶颈。需要指出的是,此时的性能瓶颈并非是虚拟点光源的数量太多,根本原因是GGX BRDF模型太过复杂。因此,如何找到新的基于物理的点光源光照模型,同时具有较低的计算复杂度,是使用立即辐射度算法来精确且高效地模拟间接光泽反射效果的一大难点。针对上述难点,需要解决以下两个关键问题。1)将具有高计算复杂度的GGX BRDF球面分布拟合为另一种计算量很小的球面分布flow,基本思路是基于线性变换球面分布这种数学思想,将GGX BRDF球面分布通过多次迭代拟合成相对简单的球面分布flow。2)将flow应用在点光源光照模型中存在大量纹理采样操作,无法直接用于间接光泽反射效果计算,否则将严重影响效率。所以需要找到一种解决方案,使本文点光源光照模型能够很好地适配立即辐射度算法,真正降低渲染间接光泽反射效果时的计算开销。
本文利用线性变换球面分布来拟合GGX BRDF,针对点光源的间接光泽反射提出一种高效算法,大幅提升了渲染效率。本文的渲染管线如图1所示,图中绿色阶段是本文的主要工作和创新点。
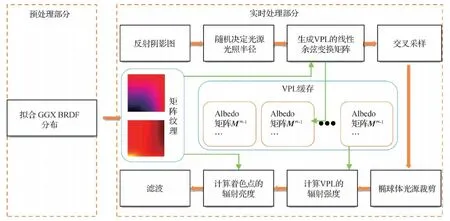
图1 本文算法渲染管线
3 基于线性变换球面分布的实时间接光泽反射
本文的核心算法是利用线性变换球面分布这种数学思想来改进GGX BRDF模型计算间接光泽反射时的缺点,提出了具有更低计算量的点光源光照模型。然后基于该光照模型,提出了更加高效的实时间接光泽反射渲染算法。
3.1 拟合GGX BRDF球面分布
GGX BRDF计算公式复杂,在立即辐射度方法中计算间接光泽反射效果(即GGX SLC算法)时开销很大。找到一个相对简单的球面分布flow代替复杂的GGX BRDF球面分布是改进GGX SLC算法非常重要的一个方向。本文发现线性变换球面分布这种数学方法可以将一种球面分布拟合为另一种球面分布。本文基于线性变换球面分布,将GGX BRDF球面分布f拟合为余弦球面分布fc。该余弦分布计算量很低,能够满足flow的要求。
将GGX BRDF球面分布拟合成为余弦球面分布的基本思路是,将粗糙度和观察角度的余弦值cosθ分别作为纹理坐标u和v,该观察角度是观察向量ωo和法线n的夹角。然后针对每一组粗糙度和观察角度,在整个半球空间上对余弦分布进行重要性采样,将采样得到的向量用线性余弦变换矩阵M变换到GGX BRDF球面分布上,然后分别计算两个球面分布在各自采样方向上的值,通过计算两个值的差异不断地迭代修正矩阵M中的元素,并将最终求得的矩阵M的逆矩阵M-1保存到纹理中。
需要注意的是,拟合球面分布属于本文算法的预计算阶段。在预计算阶段无法获取基础反射率F0。因此,在实际拟合过程中,拟合的是少了菲涅尔项F(〈ωi,ωh〉)的余弦加权的GGX BRDF,即
(2)
式中,D(〈ωh,n〉)是法线分布函数,G(ωi,ωo)是几何遮挡函数。由于ρ(ωi,ωo)少了菲涅尔项,本文单独计算了菲涅尔项对整个积分的影响ρf,然后用ρf来缩放ρ(ωi,ωo)拟合之后的结果,从而近似地弥补了菲涅尔项。ρf的计算方法为
(3)
用Fresnel-Schlick近似公式替换F(〈ωi,ωh〉),可得
ρf=F0nA+(1-F0)fA
(4)
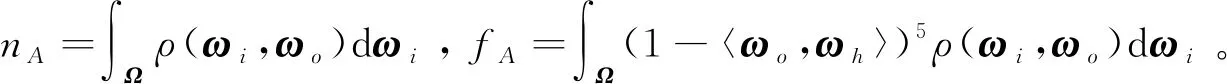
综上,通过线性变换球面分布,可以用一个余弦球面分布近似代替余弦加权的GGX BRDF球面分布,即
f(ωi,ωo)〈ωi,n〉≈ρffc(ωci)
(5)
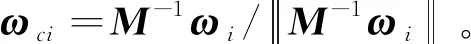
3.2 基于线性变换球面分布的单点光源光照模型
由3.1节可知,GGX BRDF球面分布f(ωi,ωo)可以拟合为余弦球面分布fc(ωci)。因此,着色点p受到的辐射亮度计算为
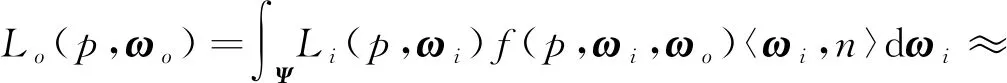
(6)
式中,Ψ表示着色点接收到的入射光线覆盖的球面区域;Ψ′是Ψ经过逆向线性余弦变换后的球面区域。由于ρf中的F0只取决于具体的着色点,nA和fA都可以从纹理中采样而得,其采样坐标只取决于观察角度以及着色点的粗糙度,所以它们都与ωci无关,可以提到积分符号外面。
式(6)是对球面上的区域Ψ的积分,如果Ψ无限小,则可以看做着色点p接收到的辐射来自一个无限小的点光源。因此,着色点接收到来自单个点光源的光照为
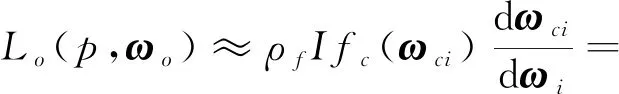
(7)
式中,I表示点光源的辐射强度。式(7)与式(6)相比,多了一项雅可比行列式dωci/dωi(Heitz等, 2016),这是因为在实际的光照计算中,由于线性余弦变换的存在,dωi和dωci对应在单位球面上的面积并不相等。
计算fc(ωci)要用到余弦分布(Heitz 等,2016),令ωnci=M-1ωi,需要注意的是,ωnci并不是单位向量,而在计算fc(ωci)时要求ωci是单位向量,所以需要先将ωnci归一化后再取其z分量,才能得到准确的fc(ωci)的值。具体为
(8)
式中,znc是向量ωnci的z分量。
结合式(7)和式(8),可得到本文最终的单点光源光照模型,该光照模型使用余弦分布计算着色点接收到的基于物理的光照。具体为
(9)
从式(9)可知,本文得到的单点光源下的光照模型只存在少量的加法、乘法、除法、矩阵和向量相乘以及求行列式等计算量较小的运算操作,而原始的GGX BRDF光照模型存在大量三角函数、开方、高次幂等非常耗时的运算操作。将该单点光源光照模型扩展至多点光源环境时,低计算量的优势进一步放大。同时,由于本文的光照模型本质上是将GGX BRDF球面分布拟合为余弦分布,所以不仅光照计算量低,而且能够实现基于物理的光照效果。
3.3 基于线性变换球面分布的多点光源光照模型
由于立即辐射度算法需要使用大量虚拟点光源计算间接光照,所以需要将单点光源光照模型扩展至多点光源环境。当着色点p接收到来自多个点光源的辐射时,利用式(9)对每一个光源贡献求和即可得到本文提出的多点光源光照模型。具体为
(10)
在式(10)表示的多点光源光照模型中,ρf和M-1仅与着色点的材质信息和观察角度相关,与具体的光源无关。因此,可以把与光源无关的参数提到求和符号外面,将式(10)化简为
(11)
式(11)即本文最终的多点光源光照模型。从式(11)可以看出,与光源数量呈正相关的操作只有少量的乘法、除法以及矩阵和向量相乘(求ωnci时需要用M-1乘以ωi),其余的运算复杂度都只是O(1)。当着色用的是GGX BRDF时,计算复杂度很高的法线分布函数D(〈ωh,n〉)、几何遮挡函数G(ωi,ωo)以及菲涅尔函数F(〈ωi,ωh〉)都与具体的光源相关,所以运算量将随光源数量呈明显的线性增长。而式(11)表示的本文光照模型,在光源数量增加时,运算量呈次线性增长。因此,本文提出的光照模型在多点光源环境下,相比于GGX BRDF多点光源光照模型具有更低的光照计算代价以及更好的光源数量可扩展性。
3.4 基于本文光照模型的间接光泽反射效果
使用立即辐射度渲染间接光照的基本思想是在直接光源照亮的物体表面上分布大量虚拟点光源,根据直接光计算出虚拟点光源的辐射强度,然后根据这些虚拟点光源的辐射强度计算出着色点的间接光照,如图2所示。为了与着色点区分,使用上标“′”表示与虚拟点光源相关的量。其中,ω′i表示直接光到虚拟点光源的入射方向,ω′o表示虚拟点光源到着色点的出射方向。

图2 使用虚拟点光源计算着色点的间接光泽反射
计算虚拟点光源的辐射强度时,可使用本文提出的单点光源光照模型,即式(9)。但是算法此处存在一个难点:尽管相比于使用原始的GGX BRDF公式少了很多耗时的运算,但由于不同的虚拟点光源对不同的着色点着色时具有不同的纹理采样坐标,会导致纹理采样次数太多,而现代GPU架构上的纹理采样是非常耗时的操作,将大幅降低渲染效率。
算法1 实时计算虚拟点光源的辐射强度
输入:由影响当前像素的虚拟点光源的索引构成的数组VPLIndexes以及数组大小Ne,虚拟点光源结构体数组VPLs,着色点位置p,矩阵纹理MatTex,直接光源的入射方向ω′i。
输出:每个虚拟点光源对当前着色点的辐射强度。
1) fori←0 toNedo;
2)Index←VPLIndexes[i];
3)F′0,α′,n′,←VPLs[Index];
4)ω′o←norm(p-VPLs[Index].position);
5)UV←calcUV(α′,dot(n′,ω′o));
6)M′-1,n′A,f′A←texture(MatTex,UV);
7)I(ω′o)←calcIntensity(ω′i,M′-1,n′A,f′A,F′0);
8) end。
其中,norm为向量归一化;position为虚拟点光源位置;UV是纹理采样坐标。
使用本文提出的单点光源光照模型计算虚拟点光源的辐射强度存在两个问题。1)纹理采样次数过多。算法1需要对每个着色点进行Ne次纹理采样,假设渲染窗口的分辨率为W×H,那么共需要的纹理采样次数为W×H×Ne。场景中的虚拟点光源数量增大会导致更多的纹理采样次数,根本原因在于同一个虚拟点光源对不同着色点着色时,每次着色都要进行一次纹理采样,因为采样矩阵纹理的纹理坐标与ω′o有关,即与具体的着色点有关。2)多次纹理采样被串行执行。算法1中Ne次纹理采样被串行执行也是该算法性能低效的主要原因之一。假设一次纹理采样所需时间为t,那么算法1在纹理采样上的时间就是Net。降低该采样时间甚至降低为t,即只耗费执行一次纹理采样所需的时间是一项具有挑战性的工作。难点是需要减少纹理采样次数,并且尽可能使这些纹理采样过程被并行执行。本文注意到,对于各向同性的物体材质,当交换入射向量ωi和出射向量ωo时,GGX BRDF值不变,即
f(p,ωi,ωo)=f(p,ωo,ωi)
(12)
同理,通过余弦分布近似计算GGX BRDF的分布值时,也具有类似的属性,即
fc(ω′i,M′-1)=fc(ω′o,M″-1)
(13)
式中,M′-1和M″-1都是从矩阵纹理中采样而得,上标“″”表示改变纹理采样坐标后与虚拟点光源相关的量。M′-1的纹理采样坐标取决于虚拟点光源所处表面点的粗糙度和ω′o与虚拟点光源处法线n′的夹角。M″-1的纹理采样坐标取决于虚拟点光源所处表面点的粗糙度和ω′i与虚拟点光源处法线n′的夹角。
结合式(9),可得虚拟点光源辐射强度的计算式,即
(14)
式中,Φ表示直接光源的辐射强度,ρ″f里面的n″A、f″A和M″-1都采自于纹理。采样坐标取决于虚拟点光源所处表面点的粗糙度和直接光入射向量ω′i与虚拟点光源处法线n′的夹角,且ω″nci=M″-1ω′o。
使用式(14)计算虚拟点光源辐射强度的好处是纹理采样坐标与具体着色点无关,只与虚拟点光源和直接光源有关,可以将矩阵纹理采样操作与着色点进行解耦。这样在一个Pass中使用计算着色器并行执行与虚拟点光源数目相等的GPU线程,每个线程根据虚拟点光源处的粗糙度以及直接光入射方向,从矩阵纹理中并行地采样出n″A、f″A以及M″-1。然后采用第2个Pass对每个着色点并行地执行光照计算,着色时与虚拟点光源相关的量只需要在GPU缓存中取出对应的n″A、f″A以及M″-1即可。
算法2 实时计算虚拟点光源的辐射强度(改进版)
输入:由影响当前像素的虚拟点光源的索引构成的数组VPLIndexes以及数组大小Ne,虚拟点光源结构体数组VPLs,着色点位置p,矩阵纹理MatTex,直接光源的入射方向ω′i。
输出:每个虚拟点光源对当前着色点的辐射强度。
Pass 1:所有虚拟点光源并行采样。
1)Index←ThreadId;
2)α′,n′←VPLs[Index];
3)UV←calcUV(α′,dot(n′,ω′i));
4)M″-1,n″A,f″A←texture(MatTex,UV);
5)VPLs[Index]←M″-1,n″A,f″A。
Pass 2:片元着色。
6) fori←0 toNedo;
7)Index←VPLIndexes[i];
8)F″0,M″-1,n″A,f″A←VPLs[Index];
9)ω′o←norm(p-VPLs[Index].position);
10)I(ω′o)←calcIntensity(ω′o,M″-1,n″A,f″A,F″0);
11) end。
其中,ThreadId为当前GPU线程索引。
与算法1相比,算法2由于纹理采样坐标与具体着色点无关,总的纹理采样次数等于虚拟点光源的总数N,远小于W×H×Ne,而且算法2中的纹理采样被诸多GPU线程并行执行,所以理论上能够将纹理采样时间降低为t。
综上,使用算法2计算虚拟点光源对着色点的辐射强度,结合本文提出的多点光源光照模型(即式(11))对着色点着色,可以高效地渲染间接光泽反射效果。
4 实验结果与分析
针对GGX SLC算法使用GGX BRDF光照模型计算间接光泽反射带来的高开销问题,实验首先验证本文提出的光照模型的正确性,然后从渲染效果和渲染效率两方面与GGX SLC算法对比,验证本文算法能够实现与GGX SLC算法相似的渲染效果,同时比GGX SLC算法具有更高的渲染效率。此外,验证了随着场景中虚拟点光源数量的增加,本文算法能够取得更大的效率提升。
实验环境为NVIDIA GeForce RTX 2070 GPU、Intel i7-9750H CPU、32 GB内存。若无特殊说明,渲染图像分辨率为1 920 × 1 080像素,虚拟点光源由分辨率为512 × 512像素的反射阴影图生成,实验使用8 × 8的交叉采样模式,使用滤波半径为16的geometry-aware滤波(Segovia 等,2006)过滤交叉采样产生的噪声,使用16×16的分块对虚拟点光源进行分块着色。本文算法和GGX SLC算法渲染得到的图像的差异使用均方根误差(root mean squared error,RMSE)来衡量。
1)本文提出的光照模型的正确性验证。由于本文间接光泽反射渲染算法基于本文提出的单点光源以及多点光源光照模型,所以需要先验证本文提出的光照模型的正确性。实验在单点光源场景验证本文提出的光照模型的正确性。场景中只有一个平面,在平面上方有一个点光源。由于实验场景只有一个点光源,在光照计算时没有使用分块着色、交叉采样等光照加速算法。实验渲染图像的分辨率为800 × 600像素。图3展示了不同粗糙度下使用本文单点光源光照模型和GGX BRDF光照模型的渲染结果。可以看出,在不同粗糙度下,本文提出的光照模型能够实现与GGX BRDF光照模型相似的渲染结果,RMSE均不超过0.002,从而验证了本文提出的光照模型的正确性。

图3 本文单点光源光照模型和GGX BRDF光照模型在不同粗糙度下的渲染结果
2)渲染效果和效率对比。为验证本文算法能否实现与GGX SLC算法相似的渲染效果,是否具有比GGX SLC算法更高的渲染效率,在Sponza、金属指环和Museum场景进行实验,渲染结果如图4所示。其中,Sponza场景使用的反射阴影图的分辨率为256 × 256像素。从图4可以看出,在3种不同场景中,使用本文算法渲染得到的最终效果与GGX SLC算法得到的非常接近,RMSE均不超过0.006,验证了本文算法能够实现与GGX SLC算法相似的间接光泽反射效果。

图4 本文算法与GGX SLC算法在不同场景下渲染效果的对比
表1为本文算法和GGX SLC算法在Sponza场景渲染最终的间接光泽反射效果过程中每个Pass的时间开销。由于在漫反射计算中,本文算法和GGX SLC算法使用的都是Lambert漫反射光照模型,因此本文算法和GGX SLC算法在漫反射计算上不存在效果和效率上的差别。通过表1可以看出,本文算法和GGX SLC算法在效率上的差异主要出现在“分块裁剪 + 光照计算”阶段,本文算法效率提升了41.0%。而两个算法使用了相同的光源分块裁剪方式,因此,渲染效率的提升源于本文算法在进行光照计算时没有使用GGX SLC算法使用的GGX BRDF光照模型,而是使用了本文的具有更低计算复杂度的间接光泽反射光照模型。

表1 本文算法和GGX SLC算法在Sponza场景中使用渲染间接光泽反射效果时每个pass的时间开销
3)虚拟点光源数量的影响。为验证场景中虚拟点光源数量增多时,本文算法相比GGX SLC算法更加具有效率优势,在金属指环场景中使用不同数量的虚拟点光源进行实验,渲染结果和效率对比分别如图5和表2所示。从图5可以看出,当虚拟点光源数量增加时,两种算法渲染得到的间接光泽反射效果都会更好,在虚拟点光源数量相同情况下,RMSE不超过0.003,两种算法的渲染效果几乎没有区别。然而随着场景中虚拟点光源数量的增加,从表2可以看出,使用本文算法渲染间接光泽反射效果时,能够比GGX SLC算法取得更大的效率提升,本质原因是本文算法在计算间接光泽反射时所用的多点光源模型中,只有少量的加法以及乘除法运算会随着虚拟点光源数量的增加而增加,其运算开销增加的速率低于GGX BRDF光照模型的运算开销增加速率,所以虚拟点光源数量越多,本文算法能够取得的效率提升就越大。

图5 不同数量的虚拟点光源对本文算法及GGX SLC算法渲染效果的影响

表2 在金属指环场景使用不同数量的虚拟点光源时,本文算法与GGX SLC算法的渲染效率对比
5 结 论
本文针对GGX SLC算法在光照计算上的高开销问题,提出了一种效率更高的实时间接光泽反射算法。该算法利用线性变换球面分布来拟合GGX BRDF,以降低BRDF的计算复杂度,并相应地给出了在单、多点光源环境下的光照模型。同时,针对多点光源环境下巨大的纹理采样开销,提出了一种纹理采样的优化策略。实验结果表明,本文算法能够实现与GGX SLC算法相似的间接光泽反射效果,而且渲染效率更高。
但是,本文算法依然存在值得继续研究和改进的地方。1)物体表面粗糙度很低时,间接光泽反射效果不连续问题。该问题是因为粗糙度很低时虚拟点光源和着色点反射的光照信息更加高频,如果虚拟点光源在表面上分布得不够密集,将很难良好地重建出连续的高频光照结果。基于立即辐射度方法,在低粗糙度下渲染出连续的间接光泽反射效果是未来的研究重点之一。2)物体几何边缘抖动现象。该抖动是由交叉采样算法造成的,在物体几何边缘上法线、位置等信息会发生高频变化,导致滤波时无法重建出良好的光照结果,从而出现抖动现象。在未来工作中,可以考虑使用Metalights(Faure 和 Chang,2010)算法降低交叉采样带来的噪声,从而降低该抖动现象。3)某些情况拟合准确性不高问题。由于本文在拟合GGX BRDF的过程中采用了Heitz中的方法,因此会遇到很多与Heitz相同的问题,例如掠射角拟合准确性不高等问题。进一步提高在不同情况下拟合的准确性,是未来的研究方向之一。
