不同理论在分析箱形梁畸变效应时的差异

王晨光，张元海

(兰州交通大学 土木工程学院，兰州 730070)

高强、薄壁、轻型化是箱形梁桥未来发展的趋势.薄壁箱梁在偏心荷载作用下的畸变效应显著，在桥梁设计过程中必须引起足够重视[1-8].张元海等[9]给出了箱形截面畸变角的一般定义，并提出了一种类似于箱梁约束扭转分析的畸变效应解析法来分析布置双层悬臂板箱梁的畸变效应.徐勋等[10]基于广义坐标法建立位移模式和几何方程，采用混合变分原理，建立了开闭口混合截面薄壁杆件扭转和畸变分析理论，以充分考虑剪切变形对箱形梁畸变效应的影响.王兆南等[11]采用板元分析法，通过建立各板元面内矩、相互约束及畸变荷载之间的关系，推导了箱形梁畸变控制微分方程.张文献等[12]对长悬臂板箱形梁的畸变效应进行了模型试验研究，通过对实测数据进行回归分析，得到长悬臂板箱形梁畸变横向弯矩的实用计算公式.Chidolue等[13]基于符拉索夫广义坐标法的基本原理求解得到了三室全斜腹板箱梁的畸变控制微分方程，并通过三角级数法计算箱形梁的畸变变形.朱力等[14]通过虚功原理构造了曲线梁的平衡方程,给出了曲梁的刚度矩阵及等效荷载矩阵.张莉[15]通过有限元软件分析了横隔板的数量及箱梁的几何特征参数对钢箱梁畸变效应的影响.畸变分析理论众多，不同畸变理论在分析箱形梁畸变效应时既有区别又有联系.本文通过对板元分析法、能量分析法这两种不同畸变理论进行比较，进一步探讨了两种理论之间的关系.

1 畸变荷载及畸变变形

在分析箱形梁畸变效应时，可沿箱梁跨度方向截取单位长度的薄片框架，其横截面简图如图1所示.图中，A、B、C、D分别为箱室的四个角点.bw、bt、bd分别为箱室腹板、顶板、底板的长度；bf为翼缘板长度；δt、δw、δd分别为顶板、腹板、底板的厚度.θ为顶板与腹板的夹角.偏心荷载P(z)作用在顶板上，偏心距为e.

作用在箱形梁横截面上的偏心荷载可以分解为正对称荷载和反对称荷载，其中反对称荷载可以继续分解为刚性扭转荷载和畸变荷载.正对称荷载和刚性扭转荷载不引起箱形梁的畸变变形，在分析箱形梁畸变效应时往往可以忽略.根据畸变荷载的自平衡条件，可得作用在箱形梁横截面上的畸变荷载如图2所示，其值分别为

(1)

(2)

(3)

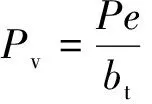
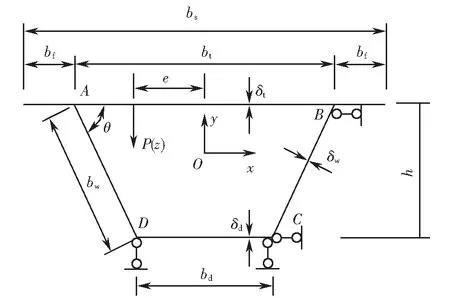
图1 箱形梁横截面简图Fig.1 Diagram of cross section of box girder

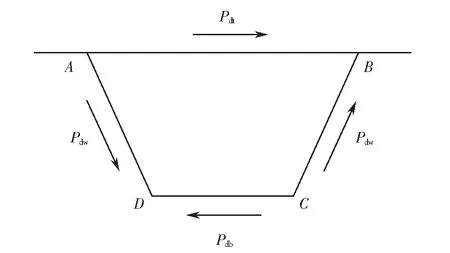
图2 畸变荷载Fig.2 Distortion Loads

组成箱形梁的各板件在畸变荷载作用下发生了平面内翘曲变形和平面外框架变形，分别如图3～4所示.定义角点D处腹板与底板夹角的改变量为γD，如图4所示，则这两种变形最终可以通过畸变角γD联系起来.

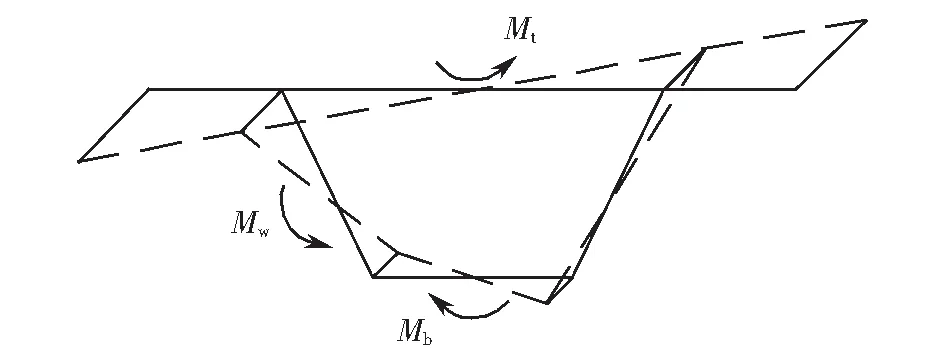
图3 平面内畸变翘曲变形Fig.3 In-plane deformation due to distortion warping

在分析畸变翘曲变形时，认为组成箱形梁各板件在发生畸变翘曲时满足平截面假定，此时，各板件平面内的位移满足初等梁理论，畸变翘曲正应力呈线性分布.由畸变翘曲正应力的自平衡条件可得，顶板、底版、腹板上由畸变翘曲正应力合成的内力矩Mt、Mb、Mw满足以下条件

(4)

(5)

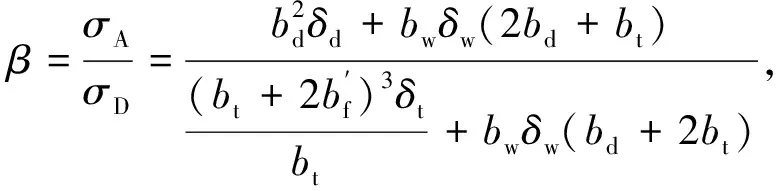
(6)

式中：E为弹性模量.

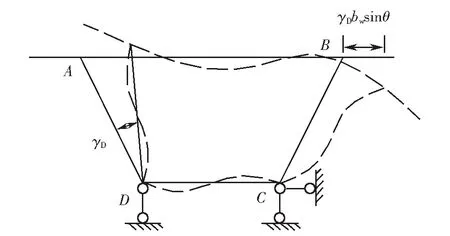
图4 平面外畸变框架变形Fig.4 Out-plane distortion deformation of the frame

当箱形梁框架产生畸变角γD时，顶板水平位移为γDbwsinθ，如图4所示.通过计算可以得到箱形梁在发生畸变框架变形时角点A、角点D处的横向弯矩mAB、mDC分别为

(7)

(8)

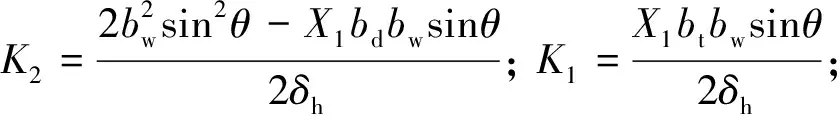
X1、δh分别为顶板作用单位水平力时的顶板跨中剪力和侧向位移，其值为

(9)

(10)

式中：X=X1/2；I1、I2、I4分别为腹板、底板、顶板的面外惯性矩.

2 板元分析法

采用板元分析法分析箱形梁的畸变效应时，将箱形梁顶板、底板、腹板离散为板元进行分析.各板元的面内力系如图5所示.

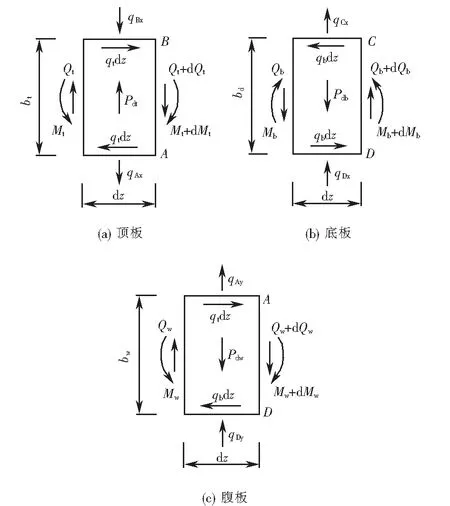
图5 各板元面内力系Fig.5 In-plane forces of each plate

由各板板元上面内力系的平衡条件，可得

(11)

(12)

(13)

dQt=Pdt-qAx-qBx;

(14)

dQb=Pdb-qCx-qDx;

(15)

dQw=-Pdw+qAy+qDy.

(16)

式中：qt、qb为微段上腹板对顶板、底板的纵向约束荷载集度；qAx、qBx为腹板对顶板的横向约束反力；qCx、qDx为腹板对底板的横向约束反力；qAy、qDy为顶板和底版对左腹板的横向约束反力；Qt、Qb、Qw为作用在顶板、底板、腹板微段上的剪力.

将式(11)、式(12)代入式(13)并微分一次，然后将式(14)、式(15)及式(16)代入，令qy=qAy+qDy；qx1=qAx+qBx；qx2=qCx+qDx可得

(17)

式(17)综合反映了畸变翘曲变形、畸变框架变形与畸变荷载之间的关系.式(17)等式左边可以拆解为与畸变翘曲变形、畸变框架变形、畸变荷载有关的三个分项W1、W2、W3，分别为

(18)

(19)

(20)

则式(17)可写为

W1-W2+W3=0.

(21)

将式(4)～(6)代入式(18)可得

(22)

式中：

箱形梁发生畸变变形时各板元的平面外力系如图6所示.图中，mAB=mBA、mDC=mCD、mAD=mDA、mBC=mCB，分别为顶板、底板、左腹板、右腹板的板端弯矩；qBy、qCy分别为框架右腹板对顶板和底板的横向约束反力.由平面外力系的平衡条件及框架横向弯矩的反对称性可得

(23)

(24)

(25)

将式(7)～(8)、(23)～(25)代入式(19)可得

W2=Γ3γD.

(26)

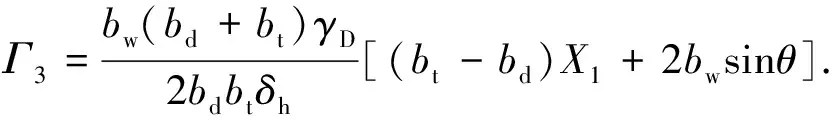
将式(1)～(3)代入式(20)，可得

(27)

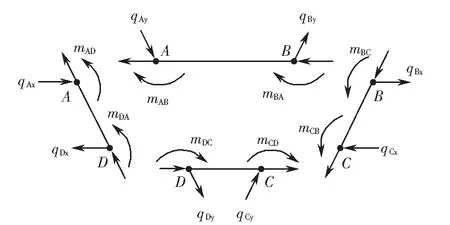
图6 板元面外力系Fig.6 Out-plane forces of each plate

(28)

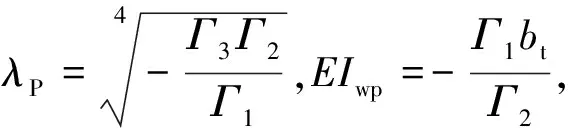
(29)

式中：λP为板元分析法中反映箱形梁抵抗畸变变形能力的几何参数；EIWP为抗畸变翘曲刚度.

3 能量分析法

采用能量分析法分析箱形梁即便效应时，同样选取畸变角γD为基本未知量，由畸变产生的内力、变形以及总势能最终均表示为γD的泛函，通过变分得到畸变控制微分方程方程.箱形梁由于畸变翘曲变形和畸变框架变形产生畸变翘曲应变能和框架畸变应变能.由式(7)～(8)可得框架畸变应变能U1为

(30)

式中：

由式(4)～(6)可得角点D处的畸变翘曲正应力σD为

(31)

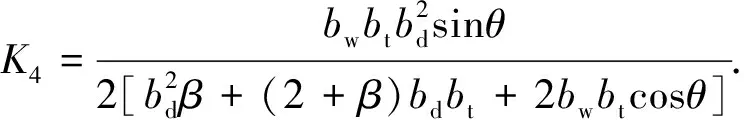
则畸变翘曲应变能U2为

在佛教中，“坐化”是指坐姿逝去。这种背景信息对英语读者来说很陌生，所以译者最好加上解释。这里译者用普通英语单词来表达文化负载词“坐化”，使读者对中国佛教文化有一个简单的了解。

(32)

式中：

箱形梁在畸变荷载作用下的外荷载势能V为

(33)

当不考虑剪切变形时，箱形梁在畸变荷载作用下的总势能Π=U1+U2+V.Π取极值的必要条件为Π的一阶变分为零.由此可得畸变控制微分方程为

(34)

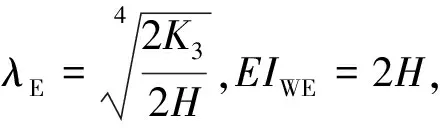
(35)

式中：λE为能量分析法中反映箱形梁抵抗畸变变形能力的几何参数；EIWE为抗畸变翘曲刚度.

通过计算可以得到，采用板元分析法和能量变分法两种不同方法计算得到的畸变几何特性参数λP、λE相等[16]，采用板元分析法计算得到的抗畸变翘曲刚度EIWP为采用能量分析法计算所得值EIWE的两倍，即满足

λP=λE.

(36)

EIWP=2EIWE.

(37)

通过对比式(29)及式(35)右边项可以得出，对于直腹板箱梁，即当bt=bd时，满足

(38)

式(38)表明，对于直腹板箱形梁，当采用板元分析法和能量变分法分析箱形梁畸变效应时，两种计算理论所得结果完全一致.

桥梁工程设计中根据不同的约束条件，关于畸变控制微分方程的边界条件可表示为如下的形式：

1) 刚性固定的支座约束

箱形梁在刚性固定支座处不能发生畸变变形，因此畸变角与畸变位移均为零：

γ=0,γ′=0.

(39)

2) 简支梁的端部设置有刚性横隔板

横隔板的约束使得箱形梁在梁段不能发生畸变变形，即畸变角为零，且在端部横截面上的畸变翘曲正应力为零:

γ=0,γ″=0.

(40)

3) 自由悬臂端且没有设置横隔板

箱形梁在自由悬臂端畸变翘曲正应力与畸变翘曲剪应力均为零：

γ″=0,γ″′=0.

(41)

4 数值算例及参数分析

文献[1]中的算例为一等截面简支箱形梁桥，其跨度L=40 m，箱形梁的横截面尺寸如图7所示.该箱梁采用弹性模量E=3.4×104MPa的C40混凝土，并在梁端设置厚度为1.2 m的横隔板.在箱形梁跨中顶板与左腹板交点处作用偏心荷载P=451.0 kN.分别采用板元分析法、能量分析法、ANSYS有限元法对该箱梁进行有限元分析计算.

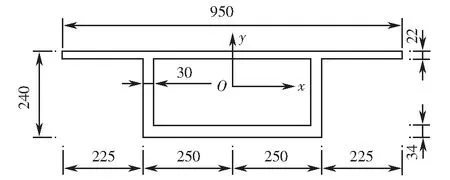
图7 箱形梁横截面简图(单位：cm)Fig.7 Cross section of box girder (unit:cm)

本例箱形梁底板与左腹板交点处畸变翘曲正应力γD随顶、底板长度之比bt/bd的变化曲线如图8所示.在分析过程中，保持箱形梁顶板长度不变，通过改变箱形梁底板长度来实现顶、底板长度之比的变化.从图中可以看出，采用板元分析法、能量分析法、ANSYS有限元法三种不同方法计算所得的畸变翘曲正应力均随顶、底板长度之比bt/bd的增大而减小，采用有限元法计算时时降低幅度最大，采用板元分析法计算时降低幅度最小.当bt/bd=1时，板元分析法和能量分析法的计算结果相同.

不同顶、底板长度之比下畸变翘曲正应力γD的计算结果如表1所列.由表1可以得到，对于本例箱梁，当bt/bd<1.4时，采用板元分析法计算所得的畸变翘曲正应力与ANSYS有限元法计算所得结果更为接近；而当bt/bd>1.8时，采用能量分析法计算所得的畸变翘曲正应力与ANSYS有限元法计算所得结果更为接近.

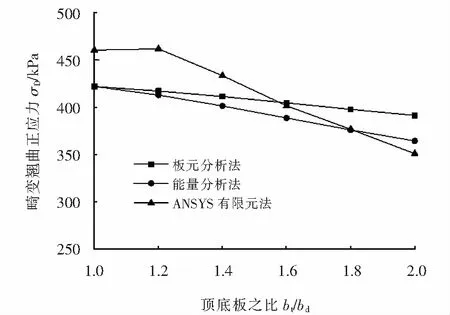
图8 畸变翘曲正应力随bt/bd的变化曲线Fig.8 Variation curve of distortion warping normal stress with bt/bd

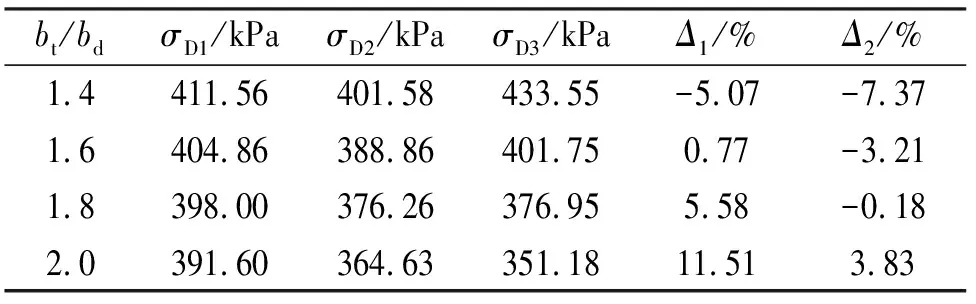
表1 不同顶、底板长度之比下的畸变翘曲正应力

5 结论

1) 本文对比了板元分析法、能量分析法在分析箱形梁畸变效时的不同，从理论上证明两种不同方法计算得到的畸变几何特性参数λP、λE相等，且对于直腹板箱梁，两种理论计算结果完全相同.

2) 采用板元分析法、能量分析法、ANSYS有限元法三种不同方法计算所得的畸变翘曲正应力均随顶、底板长度之比bt/bd的增大而减小，采用有限元法计算时降低幅度最大，采用板元分析法计算时降低幅度最小.

3) 当bt/bd<1.4时，采用板元分析法计算所得本例箱梁的畸变翘曲正应力与ANSYS有限元法计算所得结果更为接近；而当bt/bd>1.8时，采用能量分析法计算所得的畸变翘曲正应力与ANSYS有限元法计算所得结果更为接近.