基于IBA-SVM的变压器故障诊断
2021-09-09李彦哲
苏 颖,李彦哲
(兰州交通大学 自动化与电气工程学院,兰州 730070)
在电力系统输变电装置中,电力变压器是核心部件之一,它是输变电的枢纽设备.电力变压器的运行状态直接关系着电力系统的可靠性水平.其内部故障具有潜伏性等特点导致很难及时发现,因此对其做出及时准确的判断具有重要意义[1].
国内外常用的检测变压器故障方法有许多,如通过油中糠醛实验来检测绝缘材料的老化程度,通过绕组直流电阻测量反应绕组间是否存在短路,根据绝缘油中气体含量的多少及变化速度反应内部故障性质,通过红外测温方法反应内部过热情况等[2-3].大卫三角法、Roger比值法[4]、主要气体法和IEC(international electrotechnical commission)三比值法是通过气体分析而广泛应用的故障诊断方法.此类比值方法是通过描述特征气体含量间的比值并对照编码,实现对故障类型的判断.在实际中应用比值法常过于绝对,还存在部分故障类型无对应编码的问题,本身具有很大局限性,故障诊断准确率很难保证[5].随着计算机与智能技术的蓬勃发展,以支持向量机[6]、神经网络[7-8]、极限学习[9]等为理论基础的智能化诊断方法被广泛应用到变压器故障诊断中,但人工神经网络系统相对复杂,小样本数据下准确率较差.极限学习训练方便,但鲁棒性较差,不具备故障诊断的要素.支持向量机相比较神经网络等方法更具有可控性,选用合理参数有利于构造良好性能的分类器[10].
本文提出具有莱维飞行机制和增加惯性权重的蝙蝠算法通过迭代来寻找最优参数,然后构造诊断模型来实现故障分类.引入惯性权重来改善蝙蝠算法的速度更新方式,使其受上一代蝙蝠飞行速度的影响不再是固定系数;引入莱维飞行机制来改善蝙蝠位置更新,有助于跳出局部最优;最后采用改进后的算法不断迭代并根据适应度确定最终参数,最终实现基于优化后的SVM进行变压器故障诊断.
1 多分类支持向量机
SVM主要用来解决二分类问题,而电力变压器故障类型往往具有多种表现形式,在解决此类多分类问题时,一种方法是通过构造函数来实现,但构造合适的函数并进行计算极为复杂;另一种方法是从构造多个分类器入手[11].在此以图1所示的“二叉树”结构进行分类,构建5个二分类器实现多分类.根据相应国际标准以及工程实际情况,本文主要研究不同能量密度的放电故障D1(低)、D2(高)和PD(局部),不同温度等级的过热故障类型T1(<700 ℃)、T2(≥700 ℃)和NC(正常)这几类状态.
SVM能够进行分类的本质是通过将特征参量和对应状态类型作为训练样本,找到合适的支持向量,接着构造最优决策函数,将非线性函数问题转换为高维特征线性函数的问题,然后进行故障诊断.支持向量机的目标函数可以表达为:
(1)
其中:法向量ω和偏置量b共同构成超平面;ξi的引入允许样本被划分错误;C表示对错误样本的惩罚力度系数;xi为输入的样本数据;yi为故障类别.
引入拉格朗日乘子ai,得到二次规划优化问题:
(2)

图1 IBA-SVM故障诊断模型Fig.1 IBA-SVM fault diagnosis model
分类决策函数可以表达为:
(3)
支持向量机常用的核函数有多种[12],本文采用核函数的表达式如下:
(4)
由式(1)~(4)可知,对于错误分类的样本,惩罚力度C影响SVM的分类性能,惩罚越严重,训练集分类精度越高,但对于测试样本的分类效果未必最佳.核函数中引入的新参数σ影响着高斯面的宽度,宽度不同直接决定样本数据映射后的聚类程度,σ过大则各类型间不容易区分,过小则容易导致单独成类,出现过拟合现象.
2 蝙蝠算法及其改进
2.1 蝙蝠算法概述
蝙蝠算法是仿照蝙蝠群体通过改变声波特性在未知环境中寻找猎物的行为来寻找最优解的一种智能仿生算法[13].在初始狩猎阶段,蝙蝠飞行的速度和方向会随着周围环境的变化而不断发生改变,同时,狩猎的过程中其发出的波长和响度也会随之改变,波长和响度主要依据与猎物之间的距离进行调节,最后,以适应度值为评价指标,通过迭代得到问题的最优解.
蝙蝠搜索时使用的脉冲频率、速度和位置的更新公式如下所示:
fi=fmin+(fmax-fmin)·β,
(5)
(6)
(7)

蝙蝠算法在进行局部搜索时新解的计算公式如下所示:
(8)
其中:ε是随机数,取值范围为[-1,1];At为t时的平均响度.
蝙蝠发现猎物后,音强和频度都会进行相应的调整[14],具体表达式如下所示:
(9)
(10)

2.2 蝙蝠算法的改进
2.2.1 基于惯性因子的改进
蝙蝠群体在寻优过程中通过脉冲强度ri的变化实现全局搜索和局部搜索的调节,蝙蝠个体靠近解时执行局部搜索.随着迭代过程的进行,蝙蝠的速度受上一代影响系数不变,而脉冲强度ri不断增加,不能及时进行局部搜索,因此引入惯性因子μ控制蝙蝠飞行速度变化的趋势.随着寻优的进行,μ不断增大,有利于局部寻优,同时加快了收敛速度.速度更新公式如下所示:
(11)
(12)
其中:ti表示迭代进行的次数.
2.2.2 基于莱维飞行的改进
莱维飞行是一种特殊的随机运动,可以用来反映自然界反常扩散随机游走的数学模型[15].自然界中黄蜂、苍蝇等种群飞行类昆虫会采用类似的莱维飞行方式.目前已经有学者受其启发,在群体算法中引入莱维飞行来对算法进行改进,并通过对比优化结果可以得知改进后算法的精度得到了明显提升[16].这种随机游走式的路径与时间的关系可用概率密度函数表达:
Levy~u=t-λ,
(13)
其中,λ是幂次系数,1<λ<3.
利用正态分布求解随机数的方法来模拟其路径公式,表达式如下所示:
(14)
其中:β与λ的关系为β=λ-1,因此β的取值范围是0<β<2;u和m是两个服从正态分布的随机向量,可以用式(15)来表示:
(15)
在式(15)中,正态分布的标准差σu和σm的计算公式如下所示:
(16)
通过式(15)、(16)即可在实验中模拟出莱维飞行的路径.
莱维飞行的路径方向和步长均是随机的,由于飞行时方向的急剧变化和步长的不确定性,容易产生较大的跳跃性,该特点有利于蝙蝠拓宽寻优范围,及时跳出局部最优.在高维复杂空间中,该特点优势更加明显,扩大了蝙蝠的搜寻范围,避免因陷入局部最优而过早收敛,有利于提高算法的寻优能力.改进后的蝙蝠位置公式如下所示:
(17)
其中:⊗为矢量运算.
2.3 改进蝙蝠算法步骤
蝙蝠算法的改进主要包括两个方面,分别是蝙蝠算法的速度更新机制和蝙蝠算法的位移更新机制.对原本蝙蝠算法速度和位移更新机制进行改进是为了提高算法整体的搜寻能力,从而找到最适宜分类器的参数,进而提高变压器故障诊断准确率.
改进后算法流程:
步骤1:设置蝙蝠种群相关参数,随机产生蝙蝠个体的初始位置xi(i=1,2,3,…,n).
步骤2:使用式(5)、(11)、(12)和(17)更新蝙蝠的频率和速度,根据适应度值确立并保存最优解.采用变压器故障训练样本的K折交叉验证准确率作为适应度函数,表示为
(18)
式中:ltq和lq分别为测试集中被正确分类的个数和该样本总个数.
步骤3:随机产生脉冲强度,根据脉冲强度ri产生新解,如果rand>ri,则用式(8)随机游走在全局最优解附近产生局部新解.
步骤4:根据音强和适应度值迭代更新产生新解,音强和脉冲强度的更新公式如式(9)和(10).
步骤5:根据适应度确定最优解,到达规定迭代次数后停止计算.
3 基于IBA-SVM的变压器故障诊断模型
3.1 特征量的选取和量化
电力变压器在正常运行时,绝缘材料在热和电的作用下会发生老化分解的现象.当变压器发生外部难以发现的故障时,绝缘材料会受到催化而加速分解,产生烃类气体及CO2等[17].根据文献[18]及大量实测,选择C2H6、C2H2、C2H4、H2、CH4这5种气体作为特征量,并将原始数据进行标准化处理.
3.2 故障诊断的具体实现过程
基于IBA-SVM实现变压器状态判断的总体流程如图2所示,步骤如下:
步骤1:对数据做标准化处理,形成样本集合,降低含量差异对准确性的影响,处理如下:
(19)
式中:xi为原始气体浓度数据;Xi为标准化后的数据.
步骤2:设置算法基本参数并进行初始化.
步骤3:IBA对(C,σ)进行寻优,然后利用得到的参数构造多分类模型.
步骤4:利用构造的模型对变压器进行故障诊断.

图2 IBA-SVM故障诊断流程图Fig.2 Fault diagnosis process based on IBA-SVM
4 实例分析
为了验证所提方法的有效性和正确性,本文选用文献[19]中所提供的数据进行分析.选择150组气体及对应类型样本数据来验证方法的可靠性.训练集及测试集的分配如表1所列.同时,为进一步验证本文方法的优越性,将所提方法与标准支持向量机和粒子群优化支持向量机诊断进行对比研究.

表1 故障样本数据集的组成
IBA的基本参数设置如下:蝙蝠种群个数50个,最大迭代次数M为200次,脉冲强度增加系数γ和音强衰减系数α均为0.9,频率变化范围为0~2 Hz,蝙蝠初始音强均为1.5,初始脉冲强度r0为0.5,惯性因子的相关参数μmax为0.9,μmin为0.2,k为7,改进蝙蝠算法对支持向量机模型参数优化过程中,适应度值变化如图3所示.从图3中可以看出,适应度起初很小,随着迭代而逐渐增大,在第18次迭代时达到最大,随后收敛逐渐平缓并趋于一致.寻优参数值及对应分类器的准确率如表2所列,通过各个分类器的准确率可以看出,本文方法具有一定诊断能力.
将最优参数应用到IBA-SVM模型中,其测试样本分类效果如图4所示,可知该模型正确率为94%,仅有三处判断错误,D1诊断为D2,T1诊断为T2,T2诊断为D2.

图3 IBA优化的适应度曲线Fig.3 Fitness curves of the optimized IBA

表2 分类器最优参数及精度

图4 IBA-SVM故障诊断结果图Fig.4 IBA-SVM fault diagnosis classification results
为了验证本文方法的优越性,采用相同的样本数据,分别验证固定参数的SVM及PSO-SVM的分类精度,并与之比较.使用固定参数的SVM对样本集进行故障诊断时,诊断结果如图5所示.由图5可以看出,采用标准SVM进行故障诊断,T1的诊断错误率明显上升,两处分别诊断为高温过热和正常,表明该方法对于T1的划分不够细化,容易与有类似特点同为过热的故障类型混淆,并且容易忽视程度较为轻微的故障,而对于正常状态的诊断准确率也不够高.PSO-SVM的诊断结果如图6所示,整体诊断准确率较标准SVM有所提高,但对于T1的诊断优化效果不够明显,对于D1的故障类型识别没有任何提高,仍然达不到生产应用的要求.本文方法与其它两种不同方法的诊断结果对比见表3,由对比可得出本文方法对于T1、D1和D2的诊断精度明显提高,整体诊断准确率在3种方法中最高.

图5 标准SVM故障诊断结果图Fig.5 Standard SVM fault diagnosis classification results

图6 PSO-SVM故障诊断结果图Fig.6 PSO-SVM fault diagnosis classification results
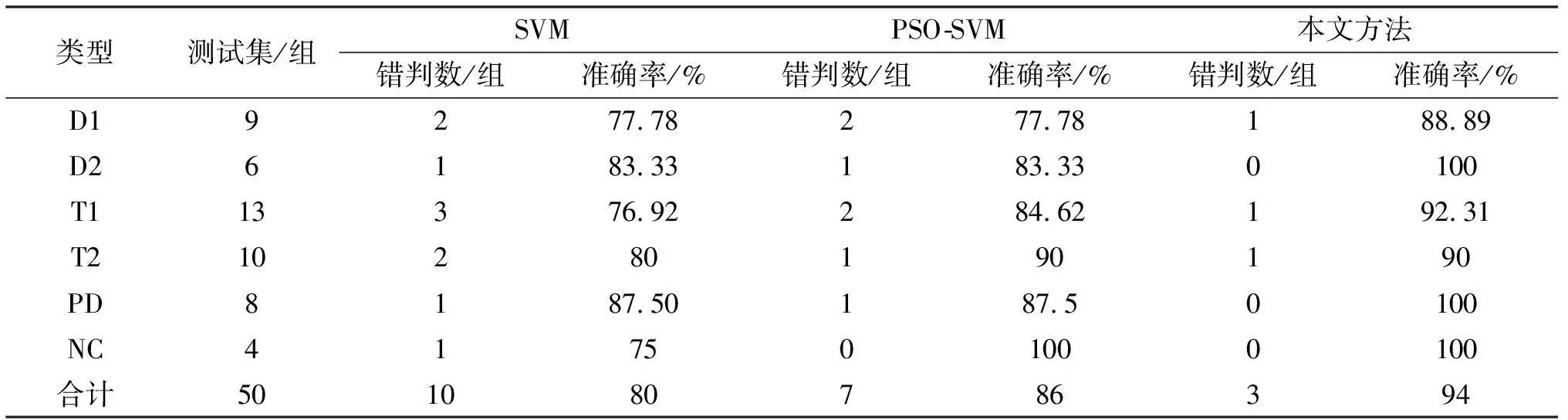
表3 不同方法结果对比
5 结论
针对电力变压器故障多样性导致诊断模型精度低、稳定性差、处理效率低等问题,提出了基于改进蝙蝠算法优化支持向量机的故障诊断方法,结论如下:
1) 在标准蝙蝠算法的基础上引入惯性权重和莱维飞行机制,算法的收敛速度及寻优精度都有效提高,证明了该改进方法的有效性.
2) 通过优化算法得到各分类器参数,采用该参数建立多种故障类型诊断模型,解决变压器故障类型与特征量之间的映射问题,诊断准确率明显提升.
3) 通过实际数据对本文所提方法进行验证,对变压器状态进行分类的精度比优化前SVM和PSO-SVM两种方法分别提高了14%和8%,故障诊断精度达到了94%,实用性更强.
