蝶形腹板剪切变形计算与分析

朱子昊，陈建兵，焦广如

（苏州科技大学 土木工程学院，江苏 苏州215011）

传统混凝土箱梁存在自重较大、施工工期较长等问题，作为替代品的波形钢腹板箱梁与钢桁架组合梁解决了上述问题，但也存在设计复杂、施工难度大等缺点。有鉴于此，国内外科研人员开发了一种新型桥梁结构——蝶形腹板混凝土箱梁[1-4]，如图1所示。其具有自重轻、造型美观、抗风性好、耐久性高等优点。蝶形腹板采用了抗拉强度高、耐久性好的高强钢纤维混凝土，腹板在纵桥向独立放置，其受力形式类似双沃伦桁架，传力机制如图2所示。目前，仅文献[2]通过理论分析发现支座处蝶形腹板所受水平剪力最大；永元直树[3]通过蝶形腹板剪切试验，提出了水平破坏强度公式，该公式计算值较试验值低20%左右，并且需对蝶形腹板受拉方向水平面积进行测量与计算，具有一定局限性。

目前，针对蝶形腹板在荷载作用下的变形研究相关报道很少，为推动蝶形腹板混凝土箱梁在国内的应用，本文根据经典材料力学理论推导出蝶形腹板在弹性阶段的剪切变形公式，并参考文献[3]建立了有限元模型，通过理论计算和有限元分析，研究了蝶形腹板在受载作用下的弹性承载力和变形规律。

1 蝶形腹板水平剪切变形计算公式的推导

当计算蝶形腹板在水平荷载作用下的变形值时，可以视为以腹板高度渐变的变截面构件在水平横向荷载作用下的位移值。在蝶形腹板剪切试件受水平横向荷载时，由于对蝶形腹板试件施加竖向荷载以限制试件产生弯曲变形与扭转变形[3]，因此计算蝶形腹板在水平横向荷载作用下的变形时，忽略弯曲变形、拉伸变形的影响，蝶形腹板在荷载作用下弹性状态时水平横向变形的计算公式可以采用荷载作用下的结构变形计算公式[5-6]，其表达式

图1 蝶形腹板混凝土箱梁结构

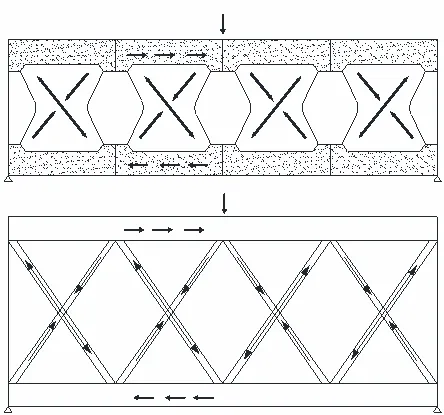
图2 蝶形腹板箱梁受力机制

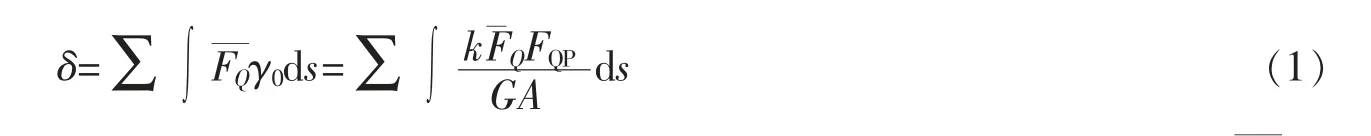
其中，G为混凝土材料的剪切弹性模量；A为蝶形腹板水平截面的面积；FQP为实际荷载施加的剪力；FQ为虚设单位荷载引起的剪力；k为截面形状系数，按矩形截面取值为1.2。式（1）中k、FQ、G均为常数，蝶形腹板由剪力引起的变形公式可转化为

对蝶形腹板截面进行划分，并将蝶形腹板受剪部分进行简化，如图3所示。图4为蝶形腹板受剪部分各段参数。水平横向荷载对蝶形腹板水平横向位移可以通过分段法求解。则变形公式可转化为

图3 蝶形腹板受剪部分的简化

图4 蝶形腹板受剪部分各段参数

蝶形腹板水平截面宽度随腹板高度线性变化，构件各段宽度变化率为

式中，li、li+1、hi分别为第i段蝶形腹板顶部宽度、底部宽度与高度。设H为蝶形腹板厚度，将各段积分区间宽度变化率带入公式（3）中，得蝶形腹板剪切变形公式

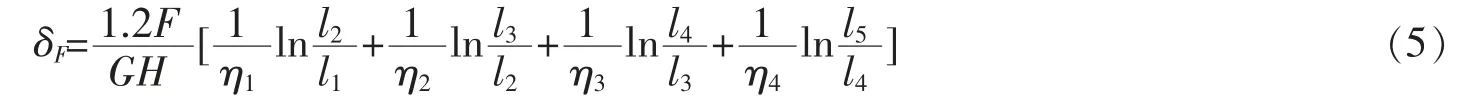
考虑到蝶形腹板中对钢筋施加的预应力Fy，其对蝶形腹板产生沿钢筋方向的压力，其受力如图5所示。预应力对蝶形腹板的影响可以分解为水平分力F1与竖向荷载F2。其中水平分力F1抵消部分水平荷载FQP。预应力为沿钢筋方向分布，其水平分力F1在各个水平方向如图6所示。对不同高度水平截面所产生的的水平力F3，即实际腹板所受剪力可通过下式计算

预应力对蝶形腹板水平横向荷载的影响可以通过公式（7）得到

式中，θ为预应力钢绞线与水平方向的夹角（见图5）。

通过积分得预应力变形公式

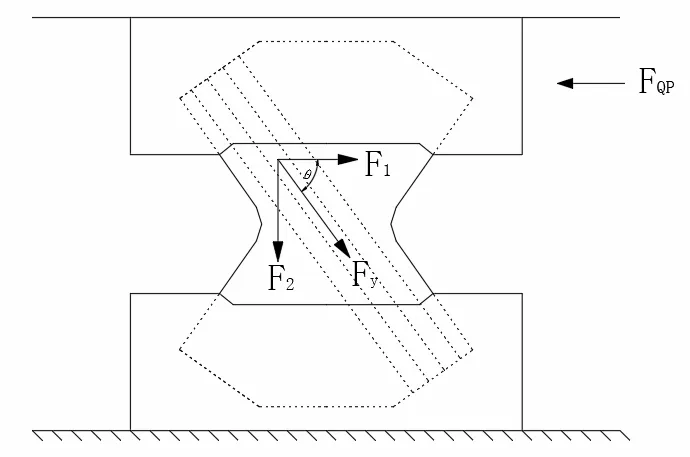
图5 预应力对蝶形腹板影响

蝶形腹板在水平横向荷载F的作用下的实际变形公式为：

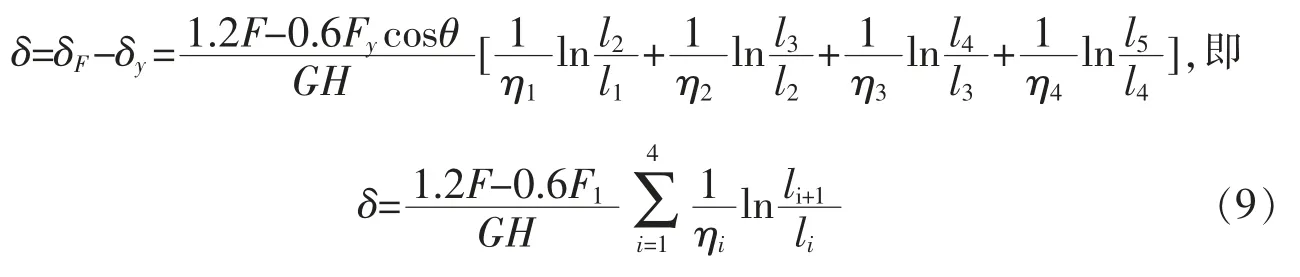
图6 预应力水平分力F1的分布

2 算例分析

2.1 试验[3]概况

以长度为38 m的蝶形腹板混凝土箱梁桥作为工程背景，对其中受剪力最大的支座处蝶形腹板作为研究对象，制作了施加蝶形腹板剪切试件，并对其进行水平剪切试验[3]。该蝶形腹板剪切试件尺寸如图7所示，其中，腹板厚度为55 mm，腹板与顶底梁使用70根长度为500 mm、直径为22 mm的HRB300钢筋作为销钉。蝶形腹板混凝土采用抗压强度为180 MPa的高强钢纤维混凝土，其弹性模量E为45 kN/mm2，蝶形腹板受拉方向布置4根直径为12.7 mm的钢绞线，并对钢绞线施加大小为291 kN的预应力。预应力钢绞线与水平夹角为53.8°。在加载过程中，将混凝土底梁固定，顶梁设置导轨，并在顶梁顶面施加竖向荷载约束蝶形腹板竖向变形，保证蝶形腹板仅产生水平变形，剪切试验加载装置如图8所示。

图7 蝶形腹板尺寸[3]

图8 蝶形腹板剪切试验[3]

2.2 基于试验[3]的蝶形腹板有限元模型

采用ABAQUS有限元软件建立蝶形腹板有限元模型，对本文推导的变形公式进行验证。混凝土采用C3D8R实体单元，钢筋采用T3D2桁架单元。蝶形腹板采用的高强钢纤维混凝土与钢绞线本构模型均按照文献[3]选取。混凝土本构模型采用CDP塑性损伤模型[7-8]，其塑性参数取值如表1所列。有限元模型如图9所示。在定义模型加载过程中，其中底梁完全固定，约束其在三个方向的位移与转动，顶梁仅X方向有有位移，即约束模型Y轴与Z轴自由度，使模型仅能在X轴方向运动。加载工况中，水平横向荷载采用位移加载。

图9 蝶形腹板有限元模型

表1 混凝土塑性模型破坏准则参数

2.3 有限 元对比分析

本文建立的有限元模型结果与文献[3]试验和有限元模拟结果对比如图10所示。从图10可以看出，本文建立的有限元模型与永元直树试验值吻合度较高，曲线变化趋势一致。

提取文献[3]试验与有限元模拟、本文建立的蝶形腹板有限元模型弹性阶段荷载值并代入剪切变形公式（9）中，得出公式计算下的变形值，如表2所示。其中蝶形腹板受剪部分简化后尺寸如图11所示。可以看出，本文推导的公式值与各试验值、有限元模拟值吻合度较高，误差均小于10%，可以较为精确地计算蝶形腹板在弹性阶段的变形。

图10 本文模型与文献[3]试验结果对比

表2 蝶形腹板变形公式对比

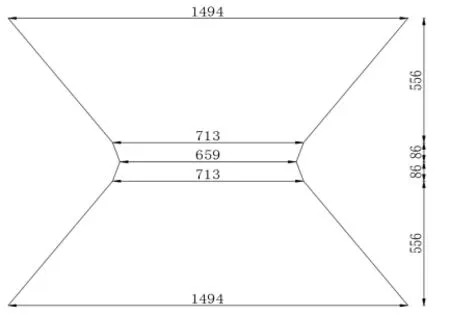
图11 蝶形腹板受剪部分简化参数

2.4 基于有限元模拟的参数分析

基于2.2节中建立的有限元模型对蝶形腹板进行参数分析，以腹板厚度为55 mm、预应力张拉荷载为291 kN的蝶形腹板有限元模型作为基准试件，仅改变腹板厚度、腹板中预应力张拉荷载，其他参数与2.2节中的有限元模型参数保持一致。不同腹板厚度与预应力张拉荷载下蝶形腹板的弹性阶段的剪切变形的公式计算与有限元分析值如表3所示。蝶形腹板在水平横向荷载作用下弹性阶段变形公式计算结果与有限元分析误差均小于10%，在允许误差范围内，具有一定参考价值。

为探究不同结构参数对蝶形腹板抗剪弹性承载力的影响，提取各模拟工况下弹性阶段荷载-变形曲线，如图12所示。由图可知，施加预应力与增大蝶形腹板厚度均能有效提高蝶形腹板弹性承载力。当腹板厚度为55 mm时，在预应力张拉荷载由0提高至150、291、400 kN的过程中，蝶形腹板弹性承载力分别提升了14%、18%、25%。腹板厚度对蝶形腹板弹性承载力有一定影响，并且有效减少了蝶形腹板剪切变形。

表3 蝶形腹板弹性阶段剪切变形有限元分析与公式计算对比

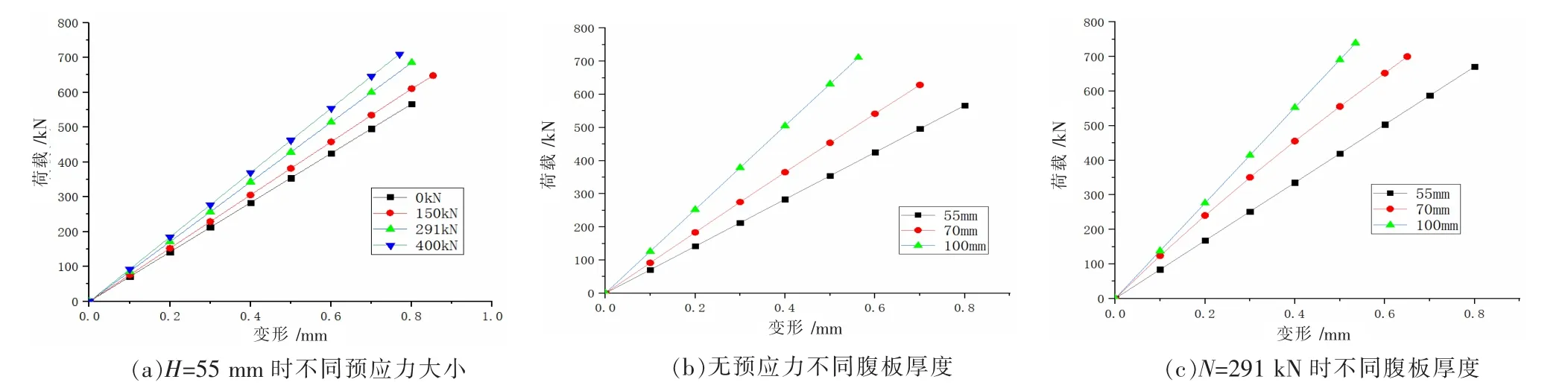
图12 荷载-变形曲线

3 结论

蝶形腹板混凝土箱梁是一种新型的桥梁结构，由于蝶形腹板在竖向结构可视为沿腹板高度渐变的变截面构件，将蝶形腹板进行简化后，通过理论推导得出弹性阶段蝶形腹板剪切变形计算公式，基于文献[3]试验建立有限元模型，并将公式计算结果与文献[3]试验结果、有限元分析结果进行了比较；再通过参数分析做了进一步研究；得出以下结论：

（1）本文推导的弹性阶段蝶形腹板剪切变形公式具有较高精度，具有一定的参考价值；

（2）使用ABAQUS有限元软件建立的蝶形腹板有限元模拟结果与文献[3]试验结果吻合度较高，可用于蝶形腹板相关研究；

（3）增大蝶形腹板腹板厚度、提高预应力张拉荷载大小均能有效提高蝶形腹板弹性承载力，减小蝶形腹板剪切变形，延缓腹板混凝土开裂，充分发挥材料性能。