一类具有饱和发生率的时滞恶意病毒传播模型的Hopf分岔

陈 实,肖 敏,周 颖,陆云翔

(南京邮电大学 自动化学院,江苏 南京 210023)

嵌入式计算、传感器监控、无线通信,以及大规模数据处理等技术的发展使得物理过程、计算过程和通信过程可以高度集成。通过将感控能力、计算能力和通信能力深度嵌入物理过程,可实现物理设备的信息化和网络化,从而产生集计算、通信和控制为一体的信息物理融合系统(Cyber-physical systems,CPS)[1-3]。它强调“Cyber-physical”的交互,涉及未来网络环境下海量异构数据的融合、不确定信息信号的实时可靠处理与通讯、动态资源与能力的有机协调和自适应控制,是具有高度自主感知、自主判断、自主调节和自治能力,能够实现虚拟世界和实际物理世界互联与协同的下一代智能系统[4]。

自1927年Kermack等[5]在研究流行于伦敦的黑死病时提出了易感者-染病者-恢复者(Susceptible-infected-recovered,SIR)仓室模型以来,病毒的传播与数学模型便开始越来越密不可分[6-9]。2010年6月,“震网”病毒的出现给伊朗境内的核工厂与众多国家内的工业企业的控制系统带来了巨大影响[10]。2012年5月28日,卡巴斯基实验室首先宣布发现了高度复杂的“火焰”病毒,这种恶意程序被用作网络武器入侵伊朗、黎巴嫩等中东国家,涉及个人、国家机构及学术和教育体系等范围[11]。这些事件使得学者们开始将恶意病毒与SIR模型结合起来,建立非线性动力学模型以研究恶意病毒在传播过程中的动力学行为[12-14],这对掌握恶意病毒的内在特性有着重要意义。目前,在对各种动力学行为的研究中,Hopf分岔(Hopf bifurcation,HB)的研究已经获得了许多重要成果[15-23]。

在恶意病毒传播模型中,时滞也起着重要作用。时滞可以用来描述恶意病毒的潜伏期,感染态节点的感染期以及恢复态节点对恶意病毒的免疫期。文献[6]研究了具有潜伏期时滞的易感者-感染者-隔离者-易感者(Susceptible-infected-quarantined-susceptible,SIQS)模型,文献[16]研究了具有临时免疫期时滞的SIQS模型,受这2篇文献的启发,本文提出了一种同时具有潜伏期时滞、感染期时滞和免疫期时滞的易感者-染病者-恢复者-易感者(Susceptible-infected-recovered-susceptible,SIRS)模型。

1 模型的建立

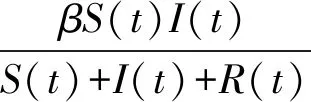
本文考虑以下具有饱和发生率的时滞恶意病毒传播SIRS模型

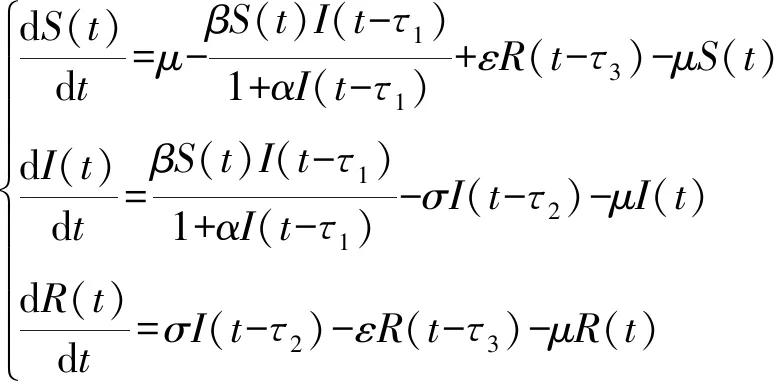
(1)

注1区别于一般的SIR模型[13,26],本文的SIRS模型考虑了从感染态恢复后的计算机节点仍有可能被感染的风险,在模型结构上形成1个环。

注2一般文章只考虑单个时滞类型,如文献[6,13]只考虑了疾病的潜伏期,文献[16]只考虑了染病个体和隔离个体的临时免疫期时滞,而本文同时考虑潜伏期时滞、感染期时滞和免疫期时滞,使得模型更加符合实际。

2 局部稳定性

通过分析式(1),可得无病平衡点E0=(1,0,0)和地方病平衡点E*=(S*,I*,R*),其中

令τ1=τ2=τ3=τ,式(1)在E*处线性化后的特征方程为

(λ+μ){λ2+(z1+2μ)λ+z1μ+μ2+e-λτ[(ε+σ-z2)λ+

z1(ε+σ)+μ(ε+σ-z2)]+e-2λτε(σ-z2)}=0

式中

显然,λ=-μ是方程的根,另2个根由式(2)决定

λ2+a1λ+a2+(b1λ+b2)e-λτ+c1e-2λτ=0

(2)

式中

a1=z1+2μa2=z1μ+μ2b1=ε+σ-z2

b2=z1(ε+σ)+μ(ε+σ-z2)c1=ε(σ-z2)

(1)当τ=0时,式(2)转化为

λ2+(a1+b1)λ+a2+b2+c1=0

(3)

假设条件(H1):a1+b1>0,a2+b2+c1>0成立,根据劳斯-赫尔维兹稳定性判据可知,式(3)的根均具有负实部。

(2)当τ>0时,式(2)等价于

(λ2+a1λ+a2)eλτ+b1λ+b2+c1e-λτ=0

(4)

设λ=iω(ω>0)是式(4)的根,带入式(4)并分离实部虚部后得

因此

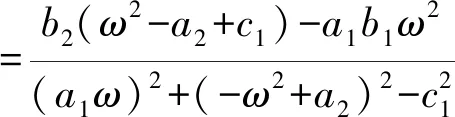
令l=ω2,根据cos2ωτ+sin2ωτ=1可以得到

l4+D1l3+D2l2+D3l+D4=0

(5)

式中

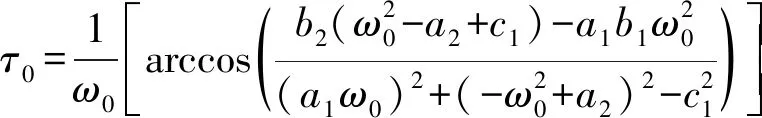
对式(4)两边关于τ求导并取倒数,可得

设λ(τ)=η(τ)+iω(τ)是式(4)的根,且满足η(τ0)=0,ω(τ0)=ω0,则有

式中

P1=b1+a1cosω0τ0-2ω0sinω0τ0

P2=2ω0cosω0τ0+a1sinω0τ0

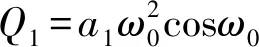
显然

假设条件(H3):P1Q1+P2Q2>0成立,于是可以得到

故满足穿越条件。

综上所述,可得到以下定理。

定理1如果条件(H1)、(H2)和(H3)成立,则有:

(1)τ∈[0,τ0)时,式(1)在平衡点E*处局部渐近稳定;

(2)τ=τ0时,式(1)在平衡点E*处发生Hopf分岔。

3 数值仿真

取μ=0.05,β=0.38,α=0.1,ε=0.15,σ=0.1,此时(H1)、(H2)和(H3)3个假设均成立。通过计算可以得到式(1)的地方病平衡点E*=(0.410 3,0.393 2,0.196 6),并得到ω0=0.178 7,τ0=9.218 4。根据定理1,下文算例验证中τ分别选取8和9.3。

图1(a)表明,在无时滞的情况下,式(1)会快速稳定到平衡点E*。图1(b)和图1(c)表明,当τ=8<τ0时,各态节点的波形图曲线最终均收敛成1条直线,相位图曲线最终收敛到1个极限点,表明式(1)在平衡点E*处是局部渐近稳定的。图1(d)和图1(f)表明,当τ=9.3>τ0时,各态节点的波形图曲线发生振荡,相位图曲线出现1个极限环,表明式(1)在平衡点E*处失去稳定性,并发生Hopf分岔。由此可知,数值仿真的结果与定理1的结论相符。

图1 式(1)的波形图和相位图

图2刻画出固定其余参数时分岔阈值τ0随各参数的变化趋势,其中分岔阈值τ0与预防效果系数α和接入退出率μ成正比,与感染率β、治愈率ε和转化率σ成反比。从图2可以看出,当α>0.1,μ>0.05时,分岔点将被滞后,反之提前;当β>0.38,ε>0.15,σ>0.1时,分岔点将被提前,反之滞后。因此可以有目的地调整系统参数使得分岔点提前或滞后,从而改变系统的动力学行为。

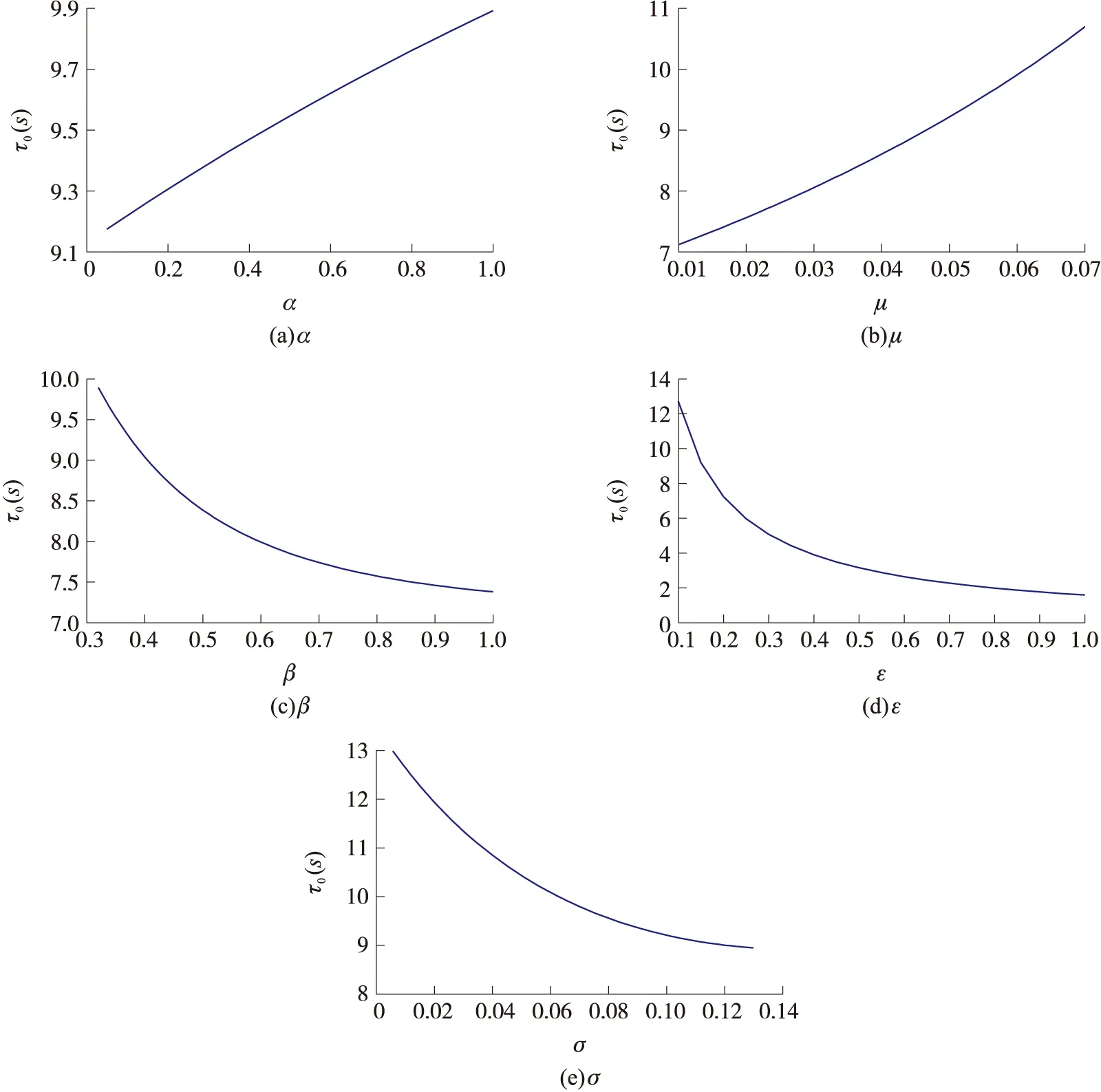
图2 τ0随各参数的变化曲线图

4 结束语

为了研究恶意病毒在CPS中的传播机理,本文利用非线性动力学理论建立了恶意病毒传播模型,并用微分动力学方程的稳定性理论推导出系统的平衡点及其稳定性条件,根据Hopf分岔定理选取时滞为分岔参数得出分岔点位置及条件。结果显示:分岔阈值与预防效果系数和接入退出率成正比,与感染率、治愈率和转化率成反比;当时滞小于分岔阈值时,系统处于稳定状态;一旦时滞大于分岔阈值,系统立刻丧失稳定性,并发生Hopf分岔现象。