基于非连续控制协议的切换耦合神经网络有限时间二分同步

梁军丽,胡元发,刘小洋,严浩远

(江苏师范大学 计算机科学与技术学院,江苏 徐州 221116)

人工神经网络是在对生物神经网络充分理解的基础之上模仿其结构与功能的一种计算模型。由于神经网络同时具有容错性、联想记忆和高效寻找最优解等功能,可以用来解决一些复杂的非线性问题,实现高效的快速运算[1]。近几十年来,神经网络已经在控制系统、信号分析与处理、交通安全和模式识别等众多领域取得了突破性的进展[2]。

随着研究的不断深入,耦合神经网络的同步问题引起了人们的研究兴趣。越来越多的网络同步概念被相继提出,如拟同步、完全同步、广义同步、指数同步、有限时间同步、固定时间同步以及簇同步等[3-6]。这些研究工作都在一定程度上推动了耦合神经网络在多个实际领域中的广泛应用。大多数耦合网络同步问题的研究往往基于网络结构保持不变的假设。事实上,在实际生活中,大多数网络结构都是实时变化的。各类网络不可避免地要在不同拓扑之间进行切换。近年来,研究人员将切换信号引入了耦合网络中,将不同信号下的神经网络看作切换系统的1个子系统。切换信号一般可为分段常值函数,不同的函数值分别代表1个子系统,该函数值将决定系统在某一时刻切换到哪个子系统。与耦合神经网络相比,切换耦合神经网络通过切换信号实现了对时变耦合网络的描述,具有更一般的实际意义[7,8],其应用领域包括通信控制、汽车行业、交通安全、电力系统等[9]。

在已有的研究中,许多研究成果均基于网络节点之间是合作关系这一假设进行讨论。事实上在实际应用中,节点之间不仅存在合作关系,还有可能存在竞争关系,如社会关系网、经济网络等[10]。此时,网络的同步问题转化为二分同步问题。与同步目标仅为单一值的完全同步相比,二分同步所考虑的问题为网络节点之间同时存在正向交互和负向交互,且网络同步目标变为绝对值相同但符号不同的1对数值[11]。另一方面,由于具有非连续激活函数的神经网络在工程应用中的广泛应用,2003年Forti等[12]提出了Filippov意义下非连续神经网络的全局收敛性,掀起了人们对具有非连续激活函数神经网络同步问题的研究热潮[13]。除此之外,众多研究耦合神经网络同步的结果对同步速度的刻画往往是渐进的,即只有当时间趋于无穷的时候,网络才能实现同步。但是在实际工程应用中,对于耦合网络究竟能够在多长时间内可以实现同步的问题的研究更加具有现实意义。随着研究的不断深入,人们逐步提出了有限时间同步、固定时间同步等概念[14,15]。这些概念有效地避免了渐进同步在收敛速度上的局限性,对实际应用具有一定的指导意义[16]。

本文主要对具有符号图的切换耦合神经网络的有限时间同步问题进行研究。针对网络拓扑为结构平衡和结构非平衡的2种情形,分别讨论具有非连续激活函数的耦合神经网络的有限时间二分同步问题。

1 网络模型与预备知识

1.1 图论

定义G={V,E,A}为N阶的无向图,其中V={v1,v2…,vN}表示节点集,边集E⊆V×V,图G的邻接矩阵表示为A=[aij],i,j∈N′={1,2,…,N}。本文主要考虑简单图,即对于任意i∈N′,均有aii=0,且aij=aji。若aij≠0,则表明节点i到节点j之间有边相连,节点vi的所有邻居节点由集合Ni={j:(vj,vi)∈E}表示。

在符号图G中,若节点集V可以划分为2个互不相交的子集V1和V2,满足aij≥0,∀vi,vj∈Vk(k∈{1,2}),且aij≤0,∀vi∈Vk,vj∈Vl(k≠l,k,l∈{1,2}),则称符号图G为结构平衡图,否则称符号图G为结构非平衡图。

1.2 集值李导数

函数U(x)关于g在x处的集值李导数定义为:LgU(x)={l∈R|∃φ∈F(g(x)),φTφ=l,∀φ∈∂U(x)}。

1.3 网络模型

考虑一类具有切换信号的耦合神经网络模型,其第i个节点(i∈N′)的动力学方程表示如下

(1)

式中:xi(t)=[xi1(t)xi2(t) …xin(t)]T∈Rn,表示t时刻第i个节点的状态向量;Dπ为n阶正定对角矩阵,Bπ表示n×n维常数矩阵;π∈M′={1,2,…,M}表示耦合网络状态的切换信号;φ代表耦合强度;f(x(t))=[f1(x1(t))f2(x2(t)) …fn(xn(t))]T∈Rn是激活函数;ui(t)表示控制器;J(t)=[J1(t)J2(t) …Jn(t)]T∈Rn表示外部输入向量;A=(aij)∈RN×N表示耦合网络的邻接矩阵,本文所考虑的网络为无向网络,即aij=aji。

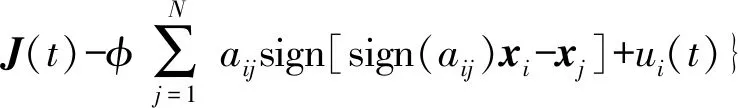
(2)

耦合神经网络式(2)的同步目标如下

(3)

式中:y(t)=[y1(t)y2(t) …yn(t)]T∈Rn为目标轨道。

引理1[17]若符号图G是结构平衡的,则存在对角矩阵R=diag{r1,r2,…,rn},ri∈{1,-1},∀i∈N′,使得RAR为非负矩阵。

假设1对于耦合神经网络式(1),激活函数f(x)满足以下条件:

(1)f(-x)=-f(x)

(2)‖F[f(x)]-F[f(y)]‖≤h1‖x-y‖+h2

式中:h1,h2>0。

2 有限时间二分同步

2.1 结构平衡图下有限时间二分同步

本节考虑结构平衡图下切换耦合神经网络的同步问题。

由引理1可知,存在对角矩阵R=diag{r1,r2,…,rn},ri∈{1,-1},∀i∈N′,使得riaijrj≥0且sign(ri)=ri,rirj=sign(aij)。

由于A为无向网络,则

(4)

定义1对于切换耦合神经网络式(2),如果存在t*>0,使得

且‖xi(t)-riy(t)‖≡0,t>t*,i∈N′,则称耦合神经网络式(2)有限时间同步到目标轨道式(3)。

记ei(t)=rixi(t)-y(t),则ei(t)=0等价于riei(t)=0。由式(2)、(3)可知

(5)

式中:ξi(t)=f(rixi)-f(y),i∈N′。

设计同步控制器ui(t)如下

ui(t)=-ρsign(ei(t))ρ>0

(6)

定理1在假设1及控制器式(6)之下,若对于任意q∈M′,均满足

(7)

(8)

则结构平衡图下的耦合神经网络式(2)有限时间同步到目标轨道式(3),其中

证明将式(6)代入式(5),可得误差系统

(9)

由于系统式(9)是非连续的,需引入微分包含理论[20]。记式(9)的右端为δi(t),并记δ(t)=[δ1(t)δ2(t) …δN(t)]T,由Filippov集值映射,可知

(10)

式中:集值函数SIGN定义为

SIGN(ej-ei)-ρ‖ei‖}

(11)

式中:αi(t)∈F[ξi](t)为可测选择。

对于无向网络,有

(12)

由假设1可得

(13)

将式(12)、(13)代入式(11),可得

(14)

利用引理3,可得

(15)

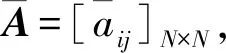
由此可得

(16)

在式(15)、(16)的基础上结合条件式(7)和(8),可得

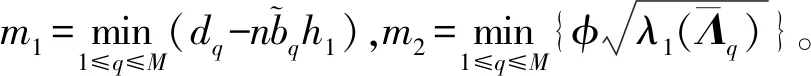
由引理2可知,耦合神经网络式(2)有限时间同步到目标式(3),且同步时间t1满足

证明完成。

2.2 结构非平衡图下有限时间二分同步

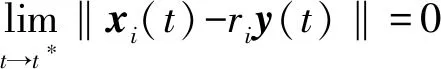
ui(t)=-ρsign(xi)

(17)

式中:ρ>0。

定理2对于结构非平衡图,在控制器式(17)以及定理1条件之下,切换耦合神经网络式(2)实现有限时间二分同步。

证明在控制器式(17)之下,耦合神经网络式(2)变为

ρsign(xi)}

(18)

选取Lyapunov泛函

并沿系统式(18)对V2(t)关于时间t求集值李导数,可得

[sign(aij)xi-xj]-2ρxiSIGN(xi)}

(19)

式中:βi(t)∈F[f(xi(t))]为可测选择。

对于任意q∈M′,对于结构非平衡的无向网络,有

SIGN[xj-sign(aij)xi]=

(20)

类似于式(13),由假设1可得

(21)

将式(20)、(21)代入式(19),可得

(22)

利用引理3,可得

(23)

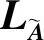
基于此,式(23)可整理为

(24)

利用条件式(7)和(8),式(22)转化为

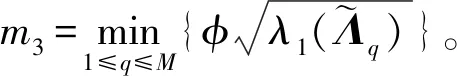
由引理2可知,耦合神经网络式(2)在控制器式(17)下将在有限时间内达到同步,同步时间t2满足

证明完成。

3 数值模拟与分析

分别考虑图1结构平衡图与图2结构非平衡图下的耦合神经网络的二分同步。

图1 结构平衡图

图2 结构非平衡图

例1考虑由5个节点构成的耦合神经网络式(2),即N=5,其网络拓扑如图1所示。将节点集划分为2个子集V1={1,3,5},V2={2,4},其对应的R=diag{1,-1,1,-1,1}。目标节点的初值y(0)=[3 2 5]T,n=3。跟随者节点的初值X(0)以及其他系统参数取值如下

X(0)=[x1(0)x2(0)x3(0)x4(0)x5(0)]T=

取切换信号为随机切换,M′=3,其中

J(t)=[0 0 0]T

f(X(t))=0.1X(t)+0.08sign(X(t))

取φ=1.2,ρ=0.9,以满足定理1的条件。由定理1的结论可知,切换耦合神经网络式(2)将在有限时间内二分同步到目标轨道式(3),结构平衡网络节点各个分量的同步仿真结果如图3所示。从图3可以看出,耦合神经网络式(2)中5个节点的各自状态x1(t),x2(t),x3(t),x4(t),x5(t)均能够在有限时间内二分同步到目标轨道状态y(t),从而验证了定理1的有效性。

图3 结构平衡网络节点的同步结果图

例2考虑结构非平衡图下切换耦合神经网络模型式(2)的同步问题,其网络拓扑结构如图2所示,耦合网络中5个节点的初值为

X(0)=[x1(0)x2(0)x3(0)x4(0)x5(0)]T=

其他参数均与例1相同,以满足定理2的条件。由定理2结论可知,切换耦合神经网络式(2)将在有限时间内达到二分同步,结构非平衡网络节点各个分量的同步仿真结果如图4所示。从图4可以看出,耦合神经网络式(2)中5个节点的各自状态x1(t),x2(t),x3(t),x4(t),x5(t)均能够在有限时间内二分同步到0,即有限时间稳定。

图4 结构非平衡网络节点的同步结果图

4 结束语

本文运用Lyapunov稳定性理论,分别针对结构平衡和结构非平衡的网络拓扑,研究了具有非连续激活函数的切换耦合神经网络的二分同步问题。通过设计非连续控制协议,提出了相应的同步判别准则,保证了耦合网络实现有限时间二分同步。本文将以往神经网络中激活函数和控制器均要求连续的情形推广到不连续的情形,同时将网络的完全同步推广到二分同步。最后通过数值实验,验证了理论研究结果的可行性和有效性。