基于指令滤波的全状态约束海洋水面船舶有限时间轨迹跟踪控制
2021-09-08胡明月于双和李云云
胡明月,于双和,李云云,阎 妍,赵 颖
(大连海事大学 船舶电气工程学院,辽宁 大连 116026)
随着科学技术的飞速发展,对海洋勘探、资源开发和运输的需求不断增加,海洋水面船舶(Marine surface vessels,MSV)的控制问题受到了广泛关注。轨迹跟踪控制是MSV运动控制中的一种典型控制方法,它要求MSV跟踪所需的时变参考轨迹。MSV的轨迹跟踪控制问题在国内外一直是热门的研究课题[1-3]。
MSV在航行过程中常常会受到如风、浪、流等外部海洋环境的干扰,这使得设计有效的控制器更具挑战性。由于扰动观测器的设计不依赖于控制器设计,且具有较高的估计精度,因此越来越受到人们的欢迎。文献[4]提出了一种固定时间扩展状态观测器,它能够精确观测船舶速度以及由模型不确定性和外部干扰构成的复合扰动,并设计了基于终端滑模的轨迹跟踪控制律。文献[5]提出了基于指令滤波的轨迹跟踪控制律,并设计了一种固定时间扰动观测器来估计包括模型不确定性和外部干扰在内的复合干扰。文献[6]提出了一种基于超螺旋算法的有限时间扰动观测器,能够在有限时间内精确估计外部时变干扰。但上述文献没有考虑MSV的输出约束和状态约束。输出约束可以保证MSV的实际路径严格限制在期望轨迹的两侧,状态约束可以保证MSV不会因偏离航线而发生碰撞或超速导致设备故障,并保证瞬态和稳态跟踪误差均在规定的小范围内。障碍李雅普诺夫函数在约束问题中得到了广泛的应用。文献[7-9]利用障碍李雅普诺夫函数设计了带有输出约束的自适应神经网络轨迹跟踪控制方案。文献[10]首次采用障碍李雅普诺夫函数结合Moore-Penrose伪逆处理了MSV在全状态约束下的轨迹跟踪控制问题。文献[11,12]利用障碍李雅普诺夫函数解决了带有全状态约束和输入饱和的MSV轨迹跟踪控制问题。文献[13]利用双曲正切函数和障碍李雅普诺夫函数解决了带有误差约束和输入饱和的有限时间MSV轨迹跟踪控制问题。文献[14]提出了基于增加幂次积分的方法和障碍李雅普诺夫函数的固定时间MSV轨迹跟踪控制律。文献[15]首次采用障碍李雅普诺夫函数结合指令滤波处理具有全状态约束的非线性系统轨迹跟踪问题。上述文献大多考虑的是具有渐进收敛性的MSV轨迹跟踪控制,导致MSV在实际应用中无法及时准确跟踪期望的轨迹。有限时间控制以其更快的收敛速度和更强的鲁棒性被广泛应用。文献[16]提出了基于非奇异终端滑模的有限时间MSV自适应轨迹跟踪控制策略。文献[17]基于反步法设计了一种欠驱动MSV自适应模糊有限时间路径跟踪控制器。文献[18]提出了一种基于有限时间微分器的有限时间路径跟踪控制方法。文献[19]基于有限时间指令滤波提出了一类非线性系统的有限时间轨迹跟踪控制方案。文献[20]解决了考虑死区和全状态约束的非线性系统的有限时间轨迹跟踪控制问题。
在文献[6,12,15]的启发下,本文提出了一种基于指令滤波器的全状态约束有限时间轨迹跟踪控制方案。首先,构造基于超螺旋算法的有限时间扰动观测器,精确观测由外部未知时变干扰和模型不确定性构成的复合扰动。与文献[11-13]相比,本文将障碍李雅普诺夫函数、有限时间指令滤波器和有限时间稳定性理论相结合来处理具有全状态约束的MSV有限时间轨迹跟踪控制问题,并且通过使用指令滤波避免了对虚拟控制律求导产生的微分膨胀和奇异性问题,最终系统是有限时间稳定的。
1 MSV系统建模
考虑带有外部扰动的三自由度MSV的动力学模型
(1)
式中:η=[xyψ]T∈R3表示大地坐标系下的位置(x,y)和偏航角(ψ);υ=[uvr]T分别代表船舶在附体坐标系下前进速度u、横漂速度v、偏航角速度r;M∈R3×3是包含附加质量的惯性矩阵;C0(υ)∈R3×3是科里奥利向心力矩阵;D0(υ)∈R3×3是非线性水动力阻尼矩阵;τ=[F1F2M3]T代表控制输入,分别由前进方向控制力F1、横漂方向控制力F2和偏航角方向控制力矩M3组成;d=[d1(t)d2(t)d3(t)]T分别代表前进方向、横漂方向和偏航角方向的外部时变干扰,J(ψ)是大地坐标系和附体坐标系之间的旋转矩阵,定义为如下形式

且满足性质J(ψ)TJ(ψ)=I,‖J(ψ)‖=1,质量惯性矩阵定义为
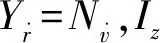

式中
d11(υ)=-Xu-X|u|u|u|-Xuuuu2
d22(υ)=-Yv-Y|v|v|v|-Y|r|v|r|
d23(υ)=-Yr-Y|v|r|v|-Y|r|r|r|
d32(υ)=-Nv-N|v|v|v|-Y|r|v|r|
d33(υ)=-Nr-N|v|r|v|-Y|r|r|r|
考虑模型参数矩阵中的不确定性,C0(υ)=C(υ)+ΔC(υ),D0(υ)=D(υ)+ΔD(υ),C(υ)和D(υ)是名义上的模型参数,ΔC(υ)和ΔD(υ)代表模型参数不确定的部分,令x1=η,x2=υ,式(1)重写为
(2)
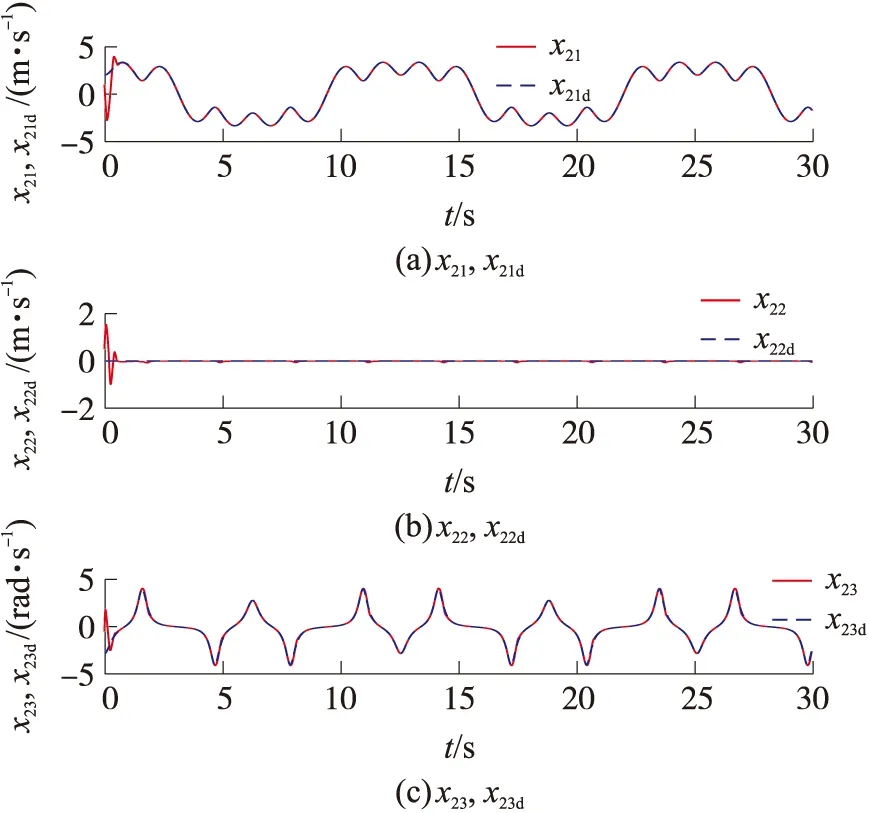
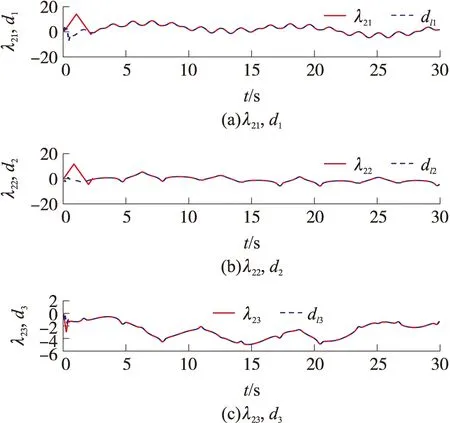
式中:dl=-ΔC(υ)υ-ΔD(υ)υ+d,表示由模型参数不确定性和未知时变外部干扰组成的复合干扰。bai>0,bci>0,i=1,2,3是预定义的常量约束。为了使船舶在有限时间内跟踪上期望轨迹并且所有的状态都被约束在|x1i| 引理1[19]对于1个连续正定李雅普诺夫函数,给出如下有限时间稳定性条件 (3) 引理2[6]基于一阶Levant微分器的有限时间指令滤波器 (4) 引理3[20]对于任意常数kb∈R+,当变量|x| (5) 引理4[19]对于所有xi∈R(i=1,2,…,n)并且0 (6) 为了估计未知复合干扰,首先引入辅助变量h1=[h11h12h13]T,h2=[h21h22h23]T (7) 式中:λ1和λ2分别为速度x2和复合扰动dl的观测值,基于超螺旋算法设计如下有限时间扰动观测器 (8) 式中:β和k是正常数。 定理1考虑式(2)MSV模型,如果复合扰动满足假设1,通过选择合适的参数β和k,扰动观测器式(8)可以在有限时间精确地估计未知的复合干扰dl。 证明结合式(2)、(7)和(8),对h1和h2求时间的导数,可得观测器估计误差动力学公式 (9) 利用障碍李雅普诺夫函数、有限时间指令滤波和反步法设计船舶有限时间轨迹跟踪控制律,在不违反全状态约束的前提下,使船舶在有限时间内跟踪期望的位置轨迹和速度轨迹。 (1)定义位置跟踪误差z1∈R3 z1=x1-xd (10) 式中:xd表示期望的轨迹,设计如下虚拟控制律α′∈R3 (11) 式中 C1=diag{c11,c12,c13}是正定对角矩阵,s1,ρ1是正常数,0<γ<1,b1=[b11b12b13]T是e1=[e11e12e13]T的约束标量,e1将在后文中定义。引入引理2中的有限时间指令滤波器,对虚拟控制律求导,可避免直接求导产生微分膨胀和奇异问题。 (12) (13) 式中:状态变量ξ2∈R3,ξ2将在后文中定义。 定义补偿跟踪误差向量e1∈R3 e1=z1-ξ1 (14) 选择e1的障碍李雅普诺夫函数 (15) 式中:当|e1i| (16) 式中:Ji∈R3,i=1,2,3表示J的第i行元素,xdi表示xd第i个元素,ξ1i表示ξ1第i个元素。 (2)定义速度跟踪误差z2∈R3 z2=x2-α′c (17) 引入文献中的[6]滤波补偿机制 (18) 式中:C2=diag{c21,c22,c23}是正定对角矩阵,状态变量ξ2∈R3,ρ2是正常数。 定义补偿跟踪误差e2∈R3 e2=z2-ξ2 (19) 根据式(11)、(17)和(19),重写式(16) (20) 根据杨氏不等式,得 (21) 式(20)最终可化为 (22) 根据式(2)、(17)~(19),可得 ρ2sign(ξ2) (23) 根据Moore-Penrose逆,得 (24) 设计如下船舶轨迹跟踪控制律 (25) 式中 k1i是正常数,i=1,2,3;s2是正设计参数;λ2是通过有限时间扰动观测器观测到的复合扰动。 定理2考虑存在外部未知干扰的MSV模型式(2),在假设1条件下,设计船舶轨迹跟踪控制律式(25),有限时间指令滤波器式(12),有限时间滤波补偿系统式(13)和式(18)。在跟踪误差初值满足e1i(0)∈Ω01{|e1i| 证明 定义障碍李雅普诺夫函数 (26) 式中:b2=[b21b22b23]T是e2=[e21e22e23]T的约束标量,对式(26)关于时间求导,并代入式(23)和(25),可得 (27) 由杨氏不等式得 (28) 根据引理3和引理4,式(28)可进一步化成 (29) 式中 (30) (31) 对式(31)求关于时间的导数,得 (32) 由引理2可知,在有限时间tf内,0<‖α′c-α′‖≤ϖ1,f=‖J‖‖α′-α′c‖,式(32)最终可化为 (33) 式中 注释R表示实数集合;R+表示正实数集;‖·‖表示欧式范数;对于a∈Rn,ai是向量a的第i个元素,其中i=1,2,…,n,|a|=[|a1| |a2| … |an|]T;λmin(·)表示矩阵的最小特征值;λmax(·)表示矩阵的最大特征值;定义x∈Rn,0<β<1,sβ(x)=[sβ(x1)sβ(x2) …sβ(xn)]T,sβ(xi)=sign(xi)|xi|β,i=1,2,…,n。 通过MATLAB仿真验证所提出的有限时间轨迹跟踪控制律的有效性。选择Cybership Ⅱ作为船模型,模型参数参考文献[12]。船舶的位置初始条件为η(0)=[0.8 1 -0.5]T;速度初始条件为υ(0)=[1 0.5 -0.5]T;有限时间扰动观测器参数为k=14,β=5;有限时间指令滤波器参数分别选为l1=20,l2=40;滤波误差补偿机制参数选择为C1=diag{5,5,5},C2=diag{5,5,5},ρ1=ρ2=1;控制器的参数选为K1=diag{10,10,10},s1=4,s2=9;误差约束的界选为b1=[1.2 0.9 1.2]T,b2=[1.7 1 1]T;时变未知扰动选为 d(t)=[d1(t)d2(t)d3(t)]T= 期望位置轨迹选择为 仿真结果如图1~9所示。由图1和图2可知,在本文FCTC方法下实际位置和速度轨迹能在有限时间内精确地跟踪上期望的位置和速度轨迹。图3和图4是ACTC方法下实际位置和速度轨迹跟踪期望的位置和速度轨迹,通过对比可知,本文FCTC方法跟踪效果优于ACTC方法。图5对比了FCTC和ACTC方法的位置跟踪误差,图6对比了两者的速度跟踪误差。可以看出,本文FCTC方法可保证位置和速度跟踪误差不超过预定的约束,FCTC方法比ACTC方法具有更快的瞬态响应,并且FCTC方法下的稳态误差比ACTC小。图7是本文FCTC方法的控制输入。图8是ACTC方法的控制输入。对比可知,本文FCTC方法的控制输入在初始阶段比ACTC控制输入大,这是因为本文控制器在开始后较短时间内驱动船跟踪上期望轨迹。图9是复合干扰及其观测值的图像,可以看出本文扰动观测器可以在有限时间内精确观测到复合扰动,这保证了MSV系统精确的干扰补偿和强鲁棒性。 图1 FCTC方法下MSV位置轨迹图 图2 FCTC方法下MSV速度轨迹图 图3 ACTC方法下MSV位置轨迹图 图4 ACTC方法下MSV速度轨迹图 图5 MSV的位置跟踪误差对比图 图6 MSV的速度跟踪误差对比图 图7 FCTC方法的控制输入曲线图 图8 ACTC方法的控制输入曲线图 图9 复合干扰及其观测值曲线图 本文研究了由外部时变干扰和模型不确定性构成的复合扰动作用下,具有全状态约束的MSV的有限时间轨迹跟踪控制问题。首先,设计了1个有限时间扰动观测器,用来估计由模型不确定性和外部扰动构成的复合扰动。利用障碍李雅普诺夫函数结合反步法构造有限时间全状态约束的轨迹跟踪控制律。此外,为了消除传统反步法对虚拟控制律求导造成“复杂性爆炸”的问题和奇异问题,引入有限时间指令滤波来对虚拟控制求导,然后采用有限时间滤波补偿机制处理滤波产生的误差,进一步减小跟踪误差,通过有限时间稳定性理论分析了本文控制策略,证实了其有效性。但本文没有考虑执行器饱和,在实际应用中,当发生执行器饱和时,船舶无法准确跟踪所需的轨迹。因此,后续研究工作将考虑输入饱和及时变外部干扰下的全状态约束有限时间船舶轨迹跟踪及编队控制。

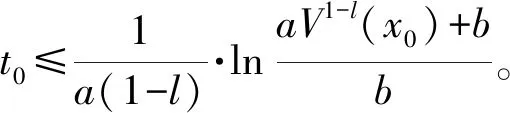

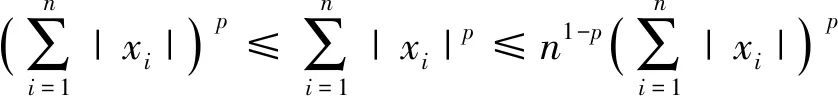
2 扰动观测器设计

3 有限时间控制器设计及稳定性分析
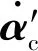





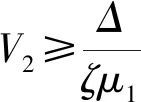

4 数值仿真
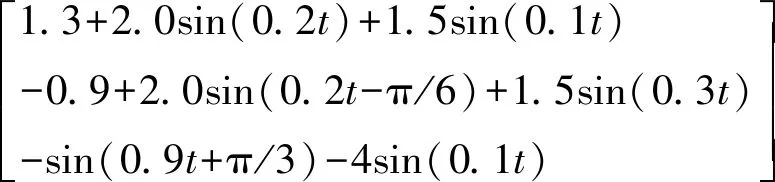







5 结束语
