基于惯性作动器的四面固支板自抗扰振动主动控制

顾仁静,李生权,朱超威,陆 路,李 娟

(扬州大学 电气与能源动力工程学院,江苏 扬州 225127)

固支板结构具有重量轻、刚度大等优点,在航天航空、汽车行业等领域中应用广泛。但是固支板在面对外部环境激励时,容易产生共振现象,导致结构疲劳破损、稳定性变差、安全性能降低等问题,因此,研究固支板的振动控制[1,2]具有重要的实际意义。目前在振动控制领域中有主动控制、主被动混合控制、被动控制3种方式。主动控制方法以现代控制理论为主要工具,结合合适的作动器和传感器进行振动控制,算法灵活,环境适应性强,具有较好的振动控制效果,在振动控制领域得到广泛应用。

目前国内外学者对于振动主动控制方法中控制器的研究也有很多,大多数使用速度负反馈、比例-积分-微分(Proportional integral differential,PID)等控制器[3-5]。尽管这些控制器结构简单、易实现,有较好的控制性能,但是容易受到外部干扰的影响,且对实际结构的数学模型精确度要求比较高,因此针对实际系统结构进行合适的控制器设计非常重要。自抗扰控制器是Han等[6]首创的非线性控制器,通过扩张状态观测器实时估计系统内部建模误差及外部激励扰动,并进行前馈补偿,抵消误差及干扰的影响。Li等[7-9]在此基础上,将自抗扰控制器进行线性化处理,减少了控制参数的个数,并使每个参数对应明确的物理意义,具有较强的鲁棒性,在振动控制上已经有了很好的控制效果。同时,在实验系统中存在的时延环节对控制效果有一定的影响,国内外学者已经提出很多先进的控制方法,以提高具有时延的系统的性能,比如采用预估控制算法对系统进行修正,设计控制补偿器进行时延补偿等[6,10]。在基于惯性作动器的四面固支板的振动控制实验中,存在系统内部控制器计算时延和传感器、惯性作动器时延以及其他一些由于机械耦合、传输特性等引起的时延,会导致控制系统产生相位滞后,降低闭环系统的稳定性,对系统的控制效果产生一定的影响。

本文针对惯性作动器的四面固支板振动系统实验中无法避免的时延环节,从系统模型的角度考虑,提出一种时延补偿的线性自抗扰振动主动控制策略。将时延环节等效为一阶惯性环节,进而建立基于惯性作动器的四面固支板结构的数学模型,并设计与系统模型阶数对应的线性自抗扰控制(Linear active disturbance rejection control,LADRC)。通过绘制Lissajous曲线得到系统的时延常数,优化自抗扰控制器的控制参数,进行前馈补偿,抵消实验中内外干扰的影响,使振动控制策略对于系统的振动抑制效果更加突出。

1 振动系统数学模型

1.1 振动系统的一般数学模型

惯性作动器是由惯性元件、阻尼元件、弹性元件和电磁感应线圈及底板进行连接组成的器件,如图1中虚线框所示。其结构简单,不需要复杂的固定方式,驱动电压小,可控性能好,因此得到越来越多的研究和应用[11]。将惯性作动器粘贴在四面固支板上,分析系统模型时,固支板粘贴处与惯性质量底板的位移速度以及加速度相同。根据图1所示系统结构,可以建立系统的运动方程

(1)

(2)

(3)

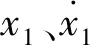
将式(3)经过拉氏变换得到

(4)

(5)

将式(5)带入式(2),主动振动控制系统的传递函数

(6)

将内外干扰总值定义为

式中

式(6)等效的二阶方程如下

(7)

最终,基于惯性作动器的四面固支板系统模型表示为

(8)

式中

1.2 具有时延补偿的系统数学模型

在基于惯性作动器的四面固支板振动控制实验中,为了消除系统时延对稳定性及控制效果的影响,从系统建模的角度分析,将时延环节进行合理等效,引入系统模型函数中,推导出具有时延补偿的振动系统数学模型。令τ表示延迟时间常数,将微分方程c(t)=r(t-τ)经过拉氏变换可得

(9)

(10)

将一阶惯性环节式(10)引入式(6)中,得到具有时延补偿的振动系统数学模型

(11)

由式(11)经过拉普拉斯逆变换得到等效的三阶运动方程

(12)

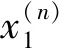
(13)

式中

2 基于惯性作动器的四面固支板时延补偿自抗扰振动控制器设计

2.1 传统自抗扰振动控制器设计

(14)

(15)

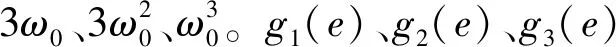
反馈控制器的系数结合线性状态误差反馈控制律(Linear state error feedback control law,LSEF)设计如下

u′0=-k′pm1-k′dm2

(16)

式中:m1、m2来自LESO的观测器状态,k′p、k′d分别为控制律中的系数。

因此控制器的整体设计为

2.2 补偿的自抗扰振动控制器设计

针对1.2节中时延补偿的系统数学模型阶数特性,设计对应的四阶扩张状态观测器,如图2所示。

图2 时延补偿的控制系统结构示意图

(17)

(18)

u0=-k1z1-k2z2-k3z3

(19)

式中:z1、z2、z3来自LESO的观测器状态,k1、k2、k3分别为反馈控制器中的系数。整体的控制器设计为

(20)

2.3 时延补偿自抗扰控制器的稳定性分析

构造的LESO为

式中

得

令hi-zi=ei,E=[e1e2e3e4],则

对于2.2节中线性状态观测器LESO

闭环系统可以表示为

y(3)(t)=f-z4-k1z1-k2z2-k3z3

(21)

3 实验验证

3.1 实验平台介绍

本次振动系统的控制对象为四面固支板结构,尺寸为500 mm×500 mm×1 mm,搭建的实验平台如图3所示。在固支板右侧布置HEV-20激振器进行外部干扰激励。利用PSV-500激光测振仪分析得到四面固支板的振型,以得到适合安置惯性作动器的最大应变处。利用同位配置的原则,将CA-YD-160型压电集成电路(Integrated electronics piezo electric,IEPE)加速度传感器贴在四面固支板上。NI PCIe-6343采集的信号将经过恒流源适配器放大,并输入Simulink里的desktop real-time环境下的Analog Input模块里,产生控制量之后由Analog Output模块经NI PCIe-6343采集卡和功率放大器对惯性作动器产生实际的电压控制信号,实现对四面固支板振动的抑制。本文使用的惯性作动器是来自德国厂商VISATON的EX45S。实验中惯性作动器的参数如表1所示。

图3 实验平台照片

表1 惯性作动器参数表

3.2 系统延迟时间τ测量

在本次实验中,激振四面固支板使用的信号是46.5 Hz,因此在测量本套实验系统的延迟时间常数τ时,令f=46.5 Hz,绘制采集的输入输出信号,如图4所示。

采用式(22)的正弦函数来逼近图4所示的振动系统输入和输出数据,同时将式(22)中的u作为横坐标,y作为纵坐标,绘制出Lissajou图形。

图4 系统的输入信号和输出信号图

u=5sin(2πft)

y=sin(2πft+h)+d

(22)

图5 Lissajou图

3.3 不同控制器振动控制效果

已知基于惯性作动器的四面固支板系统的延迟时间常数为5.99 ms,分别利用PID控制器、传统自抗扰控制器和时延补偿自抗扰控制器对四面固支板的振动进行控制实验。使用经典的试凑法调节控制器参数,选取处于抑制效果最好的临界状态的参数值进行比较分析。PID控制器的参数为kp=1.5,ki=0.0045,kd=0.085;传统三阶LADRC参数为k′p=200,k′d=56,b0=3.827,ω0=45;考虑延时环节的四阶LADRC参数为k1=56,k2=4.35,k3=0.56,b=639,ωc=10。

分别在系统中加入PID控制器、传统三阶LADRC和时延补偿四阶LADRC,采集到控制前后的振幅对比如图6所示。受控前,四面固支板结构的传感器输出电压为5.3 V,在加入了PID控制器之后,减小至1.8 V,相对减少了66.03%;加入了传统三阶LADRC之后,传感器输出电压降至1 V左右,减少了84.91%;在加入了时延补偿四阶LADRC之后,传感器输出电压减小至0.9 V,相对减少了86.79%。通过图7可以明显看出使用LADRC对振动抑制的效果优于使用PID控制器,同时,时延补偿的四阶LADRC振动抑制效果更好,说明本文设计的控制器对振动具有较强的抑制效果。

图6 不同控制器对应的输出图

图7 5～6 s处输出放大图

同时对采用不同控制器的系统输出的信号做快速傅里叶变换(Fast Fourier transform,FFT),结果如图8和9所示。在频率46.97 Hz处,幅值降低的程度十分明显。此处加入PID控制器,采集的信号共振幅值由12.58 dB降至1.63 dB,总计减少了10.95 dB;此处加入传统三阶LADRC,采集的信号共振幅值由12.58 dB降至-2.33 dB,总计减少了14.91 dB;此处加入时延补偿的四阶LADRC,采集的信号共振幅值由12.58 dB降至-3.42 dB,总计减少了16.00 dB,进一步说明了3种控制器的控制效果。数据分析见表2。

图8 不同控制器的FFT振幅图

图9 46.97 Hz处FFT振幅放大图

表2 不同控制器的输出振幅表

4 结束语

通过3.3节中实验结果及表2的数据分析可以得出,LADRC明显优于PID控制器的控制效果。同时通过FFT分析,进一步可以看出,时延补偿的四阶LADRC的效果略优于传统三阶LADRC,验证了本文提出的时延补偿的线性自抗扰振动主动控制策略能够较好地抑制四面固支板的振动,具有良好的抗干扰能力和振动控制性能。