基于滑模观测器的四旋翼无人机全回路解耦控制

赵振华,肖 亮,曹 东,张 朋

(1.南京航空航天大学 自动化学院,江苏 南京 211106; 2.重庆邮电大学 工业物联网与网络化控制教育部重点实验室,重庆 400065; 3.东南大学 复杂工程系统测量与控制教育部重点实验室,江苏 南京 210096)

无人机因其成本低、灵活性高、无人员伤亡等优点被越来越多地应用于航空侦察、灾害救援等领域[1]。四旋翼无人机以其独特的悬停、垂直起降能力,在战术侦察、精确起飞、定点监视等军事和经济领域得到了广泛的应用[2]。四旋翼无人机经常通过跟踪某一轨迹来执行特定任务,因此高精度的轨迹跟踪控制是四旋翼无人机的关键技术[3]。然而,四旋翼无人机系统动态跟踪误差的本质非线性和不同通道强耦合特性给系统控制设计带来了巨大挑战[4]。此外,随着飞行环境的日益复杂,外部干扰、模型不确定性和未建模动态干扰等多源干扰也严重限制了四旋翼无人机控制系统的跟踪精度。

为了应对四旋翼无人机轨迹跟踪控制的挑战,国内外研究人员提出了很多有效的控制方法:在线性化模型的基础上,文献[5]对比了比例-积分-微分算法和线性二次调节等传统控制方法。虽然上述方法实现了四旋翼无人机的悬停控制,但当参考轨迹为三维轨迹时,轨迹的跟踪精度会急剧下降。为了减小非线性和多源干扰的影响,文献[6-9]基于四旋翼无人机的非线性模型,结合先进的非线性控制算法,提出了多种轨迹跟踪控制策略。文献[6]采用非线性鲁棒控制方法设计四旋翼无人机的轨迹跟踪控制器,在系统存在消失不确定性的情况下,依然能够保证系统轨迹跟踪误差收敛。文献[7]提出了一种基于优化滤波器的自适应输出反馈控制方法,并通过轨迹跟踪实验验证了该方法对时延和噪声的鲁棒性。在文献[8]的研究中,将反步设计方法与参数调度技术相结合,提出了一种参数调度的四旋翼无人机姿态跟踪控制方法,并通过实验对所提算法进行验证。文献[9]将四旋翼无人机轨迹跟踪控制问题转化为姿态和位置回路的指令跟踪问题,并在位置和姿态回路分别采用模型预测控制和H∞控制策略,仿真结果表明,所提组合控制方案保证了受扰四旋翼无人机的跟踪误差在稳态时收敛到0。然而,需要注意的是,上述方法都以鲁棒的方式处理多源干扰,意味着对干扰的鲁棒性是以牺牲标称控制性能为代价获取的。

基于干扰观测器控制(Disturbance observer based control,DOBC)[10]因其独特的补丁特性而受到广泛关注[11]:当系统受到干扰影响时,该控制策略可以基于干扰的估计值,通过对干扰进行补偿的方式,实现抑制干扰影响的目标;当系统中没有干扰时,由于干扰的估计值为0,对干扰的补偿亦为0,此时系统能够保持原有基准控制器的标称性能。受DOBC控制设计理念的启发,基于干扰观测补偿的四旋翼无人机复合轨迹跟踪方法得到了发展,如基于线性干扰观测器的复合比例-积分-微分控制方法[12],基于扩展状态观测器的自抗扰方法[13]。当系统中的干扰为常值或慢变干扰时,上述控制方法可以显著提升受扰四旋翼无人机系统的轨迹跟踪精度。考虑到四旋翼无人机空中飞行过程中不仅会受到外界阵风等环境干扰,还会受到内部机械摩擦等未建模动态干扰以及气动参数摄动等不确定性的影响,因此其受到的干扰大多数不满足慢变或常值的假设条件,现有的基于DOBC的轨迹跟踪控制方法无法直接使用。

本文针对受时变干扰影响的四旋翼无人机轨迹跟踪控制问题进行研究,提出了一种基于滑模观测器的全回路轨迹跟踪解耦控制方案:首先,基于串级控制的理念,将四旋翼无人机的轨迹跟踪问题转化为位置回路和姿态回路的指令跟踪问题;其次,将四旋翼无人机所受到的多源干扰视为集总干扰,分别在位置回路和姿态回路设计高阶滑模观测器(High-order sliding mode observer,HSMO),以实现时变集总干扰的高精度估计;而后,基于干扰估计信息和动态逆控制算法,分别在位置和姿态回路构造复合动态逆控制器;最后,将位置回路和姿态回路的虚拟控制量转换为无人机的旋翼转速这一真实控制量。本研究实现了不同通道之间的解耦控制,避免了不同通道控制作用的相互影响;实现了时变干扰的高精度估计,保证了时变干扰存在情况下旋翼无人机的高精度跟踪。

1 系统建模与问题描述

首先给出了四旋翼无人机升力产生原因和六自由度动力学模型,然后引出无人机轨迹跟踪问题,并将其转化为位置环和姿态环的指令跟踪控制问题。

1.1 四旋翼无人机建模

如图1所示,四旋翼无人机包含4个转速可调的独立旋翼,通过调节4个旋翼的转速实现其位置和姿态运动。为便于描述四旋翼无人机的运动,引入图1中2个坐标系:地面坐标系(Oe,Xe,Ye,Ze)是用来描述四旋翼无人机位置的惯性坐标系,机体固连系(Ob,Xb,Yb,Zb)用来描述姿态角(滚转角φ、俯仰角θ和偏航角ψ)和沿坐标轴ObXb、ObYb、ObZb旋转的角速度ωx、ωy、ωz。机体固连系(Ob,Xb,Yb,Zb)的坐标原定固连在无人机的质心,X和Y轴分别指向旋翼1和旋翼2,Z轴与X和Y轴满足右手定则。

图1 四旋翼无人机旋翼结构示意图

4个旋翼转速同时增加,无人机升力增大,产生竖直向上运动的趋势;旋翼2、4转速分别增大和减小,旋翼1、3转速保持不变,则无人机绕Xb轴转动,滚转角φ有增大的趋势;旋翼3、1转速分别增大和减小,旋翼2、4转速保持不变,则无人机绕Yb轴转动,俯仰角θ有增大的趋势;旋翼1、3转速增大,旋翼2、4转速减小,则无人机绕Zb轴逆时针旋转,偏航角ψ有增大的趋势。定义无人机4个旋翼的转速分别为ω1、ω2、ω3、ω4,沿Zb轴的总升力为UL,绕机体ObXb、ObYb、ObZb的轴转动力矩分别为τx、τy和τz,则可以得到

(1)

式中:kL为升力系数,b为反扭矩系数,l为旋翼中心到无人机质心的距离。

假设四旋翼无人机为刚体,则可以得到其六自由度动力学模型为

(2)

(3)

(4)

式中:Jx、Jy和Jz为3轴转动惯量,τdx、τdy和τdz为外部干扰力矩,x、y、z代表无人机质心在惯性坐标系下的位置,m为无人机质量,g为重力加速度,kt为阻力系数,Fdx、Fdy和Fdz代表外部干扰力,axu、ayu和azu为位置回路的虚拟控制量,具体计算如下

(5)

1.2 问题描述与控制问题提炼

(6)

定义四旋翼无人机的位置跟踪误差为

ex=x-xdey=y-ydez=z-zd

则根据方程式(4)可以得到位置动态跟踪误差为

(7)

为方便书写,将姿态回路模型式(2)和式(3)写为如下的紧凑形式

(8)

式中:

定义姿态角跟踪误差为

eΘ=Θ-Θd=[φ-φdθ-θdψ-ψd]T

则根据方程式(8)可得姿态角动态跟踪误差为

(9)

针对式(9)姿态环动态跟踪误差,定义如下变量

则方程式(9)可写为

(10)

通过上述变换,将四旋翼无人机的轨迹和航向角跟踪问题转化为式(7)位置环跟踪误差ex、ey、ez和式(9)姿态环跟踪误差eΘ的镇定问题。

注2通过引入新的变量,姿态环动态跟踪误差由方程式(9)转化为方程式(10),在形式上实现了3通道之间的解耦,方便了控制器的设计;式(7)位置环动态跟踪误差也在形式上实现了3通道之间的解耦。

2 控制器设计

首先基于有限时间观测器技术,针对位置环和姿态环设计有限时间观测器,实现位置环集总干扰估计以及姿态环姿态角跟踪误差变化率和集总干扰的估计;然后基于估计信息,结合动态逆控制算法,设计复合动态逆控制器,实现四旋翼无人机的解耦控制。

2.1 有限时间观测器设计

假设1式(7)位置环动态跟踪误差中外部干扰力Fdx、Fdy、Fdz和式(8)姿态环动态跟踪误差中外部干扰力矩τdx、τdx、τdx是可微的,并且其导数是有界的,即

(11)

式中:ld1、ld2、ld3和ld4、ld5、ld6是正常数。

为了估计外部干扰Fdx、Fdy和Fdz,针对式(4)位置回路动态跟踪误差设计有限时间观测器

(12)

(13)

(14)

(15)

分析式(10)姿态环动态跟踪误差,根据假设1可以得到存在正常数lAo1、lAo2、lAo3使得

(16)

(17)

(18)

(19)

定义姿态环观测器式(17)～(19)的估计误差

(20)

2.2 复合解耦控制器设计

定理1针对式(7)位置环跟踪误差子系统,设计复合解耦控制器

(21)

考虑到位置环的控制是通过改变姿态角来实现的,因此姿态回路的期望值Θd是基于位置回路虚拟控制量axu、ayu和azu并根据方程式(6)计算所得。

定理2针对姿态环跟踪误差子系统式(10)设计复合解耦控制器

(22)

由于四旋翼无人机的控制执行机构为4个旋翼转子,因此整个闭环系统的最终控制量为4个旋翼的转速ω1、ω2、ω3和ω4。四旋翼真实控制量可以根据式(1)由UL、τx、τy、τz计算得到

(23)

式中:UL由控制器式(21)和变换式(6)计算得到,τx、τy和τz由控制器式(22)和变换式(10)计算得到。四旋翼无人机系统全回路解耦控制结构框图如图2所示。

图2 四旋翼无人机系统全回路解耦控制结构框图

3 稳定性分析

从式(23)可以看出:如果定理1和2得到证明,四旋翼无人机全回路系统的真实控制量ω1、ω2、ω3和ω4就能保证四旋翼无人机渐近跟踪到其参考轨迹和期望航迹角,因此后续证明过程中,只需证明定理1和2即可。

从式(7)、(9)系统动态跟踪误差和式(21)、(22)控制器的形式可以看出:位置环和姿态环在其3通道上均存在明显的对称形式,因此证明定理1和2的过程可以只证明某一通道跟踪误差渐近收敛。不失一般性,本文通过证明axu保证位置环X轴向位置跟踪误差ex渐近收敛来证明定理1。以下分为2个部分进行证明:

(1)Fdx被精确估计后,位置环跟踪误差ex渐近收敛。

考虑到方程式(15),把控制器式(21)代入式(7)位置动态跟踪误差系统得到

(24)

由于干扰估计误差edx能够在有限时间内收敛到0,所以存在1个有界常数tx,满足当t≥tx时,干扰估计误差edx=0能够保持。当t≥tx时,方程式(24)中的位置跟踪误差ex的闭环动态值变为

(25)

就闭环系统式(25)定义如下Lyapunov函数

(26)

考虑到动态方程式(25),对Lyapunov函数式(26)求导可以得到

(27)

(2)Fdx被精确估计前,状态在有限时间内不逃逸。

从上述证明中可以得到,在控制器式(21)作用下,跟踪误差系统式(7)的状态是有界的,并且当干扰被精确估计后,位置跟踪误差ex渐近收敛到0。因此控制器式(21)中axu能够保证位置跟踪误差ex渐近收敛,类似地可以证明ayu和azu分别保证位置跟踪误差ey和ez渐近收敛。

4 仿真分析

4.1 仿真设定

为了验证所提算法的有效性,本部分基于四旋翼无人机的模型数据,分别对所提出的复合解耦控制器和传统的干扰观测补偿的动态逆控制器进行数字仿真测试。四旋翼无人机本体结构参数如表1所示,位置姿态初始值设定为

表1 四旋翼无人机本体结构参数表

x(0)=0y(0)=1z(0)=0

θ(0)=0φ(0)=0ψ(0)=0

p(0)=0q(0)=0r(0)=0

需要跟踪的参考轨迹设定为特定复杂的轨迹圆柱螺旋曲线,该轨迹随时间变化的方程为

xd=sin(0.5t)yd=cos(0.5t)zd=2+0.1t

参考航向角设定为ψd=15°cos(0.5t)。为了使仿真测试更具有挑战性,设定四旋翼无人机在仿真过程中受到的集总干扰为时变干扰。干扰设定为

Fdx=-4sin(0.3πt)Fdy=2.4sin(0.3πt)

Fdz=2.4sin(0.3πt)τdx=-Ixsin(0.2πt)

τdy=Iysin(0.2πt)τdz=-2Izsin(0.2πt)

所提出的复合解耦控制器的具体表达形式为方程式(21)～(22),其中观测器设计形式为方程式(12)～(14)和方程式(17)～(19),仿真过程中观测器增益和控制器参数分别设计为

kP11=kP21=kP31=4kP12=kP22=kP32=4

lpo1=10lpo2=10lpo3=10

kA11=kA21=kA31=12kA12=kA22=kA32=36

lAo1=300lAo2=500lAo3=100

传统的非线性控制器具体形式为

4.2 仿真结果分析

图3和图4分别给出了在本文复合解耦控制器和动态逆控制器作用下的四旋翼无人机三维轨迹跟踪响应曲线和单轴位置跟踪响应曲线。从图3可以看出,本文控制方法可以保证圆柱螺旋曲线复杂轨迹的高精度轨迹跟踪,传统的动态逆控制算法显著地偏离了参考轨迹。从图4可以看出,相较于传统动态逆控制算法,本文算法显著提升了旋翼无人机在3个轴向的位置跟踪精度,将三轴位置跟踪误差稳态值从2 m缩小至0.05 m。

图3 轨迹跟踪响应曲线图

图4 位置回路跟踪响应与跟踪误差曲线图

图5给出了姿态回路虚拟参考指令的跟踪效果。从图5中可以看出,由于需要跟踪的轨迹较为复杂,内环需要跟踪的姿态角指令也为时变复杂指令,因此指令跟踪控制具有一定的挑战性。图5(b)、(d)、(f)中的姿态角指令跟踪误差曲线清晰地展示了本文控制算法可以显著地提升姿态环指令跟踪精度。图6展示了高阶滑模观测器的干扰估计效果,位置环集总干扰Fdx、Fdy和Fdz可以在短暂的时间内(2.5 s)被高精度估计。图7给出了4个旋翼的转速响应曲线。从图7可以看出4个旋翼的最大转速小于4 000 r/min,并且转速没有发生突变,说明本文控制算法能够符合工程实际。从图7也可以看出,复合解耦控制算法和动态逆控制算法的旋翼转速响应曲线较为相似,说明是在同等能量情况下对2种控制方法进行比较的,验证了对比的合理性。

图5 姿态回路跟踪响应与跟踪误差曲线图

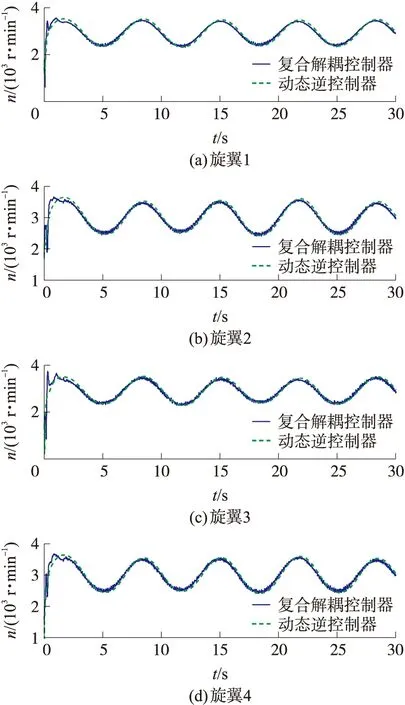
图7 旋翼转速响应曲线图

5 结束语

本文针对受时变干扰影响的四旋翼无人机复杂轨迹跟踪控制问题进行研究,综合考虑旋翼无人机位置、姿态环动态跟踪误差和执行机构模型,提出了一种基于滑模观测器的全回路轨迹跟踪解耦控制方案。首先将四旋翼无人机轨迹跟踪控制问题转化为位置回路和姿态回路的指令跟踪问题;其次将不同通道之间的耦合以及多源干扰影响视作集总干扰,并基于高阶滑模观测器对其进行估计;而后基于干扰估计信息和动态逆控制算法,分别在位置和姿态回路构造复合动态逆控制器;最后将位置回路和姿态回路的虚拟控制量转换为旋翼转速。本文控制方案实现了旋翼无人机位置回路和姿态回路不同控制通道之间的解耦,在保证各个通道设计独立的前提下,实现了轨迹的渐近跟踪。针对圆柱螺旋线轨迹跟踪的仿真结果验证了本文解耦控制方案的有效性。