基于迭代学习观测器的无人机故障鲁棒控制*

贺佳辉，付兴建

（北京信息科技大学，北京 100192）

0 引言

四旋翼无人机是一种能够不载人自主飞行的特殊飞行器，四旋翼无人机具有机动性能高，运动灵活，可在狭小的空间范围内飞行等优点，四旋翼无人机发展的很快，被大量应用于各行各业［1］。伴随着科技的发展，四旋翼无人机在微小化、智能化方面取得了前所未有的发展。

四旋翼无人机的鲁棒性、安全性和可靠性是无人机搭载更多功能的前提和基础。四旋翼无人机是一个具有欠驱动性、非线性、强耦合性等特性的复杂系统［2］，并且在飞行过程中会受到外界环境的干扰，甚至四旋翼无人机的执行器会发生故障。从四旋翼无人机面世至今，国内外针对四旋翼无人机的控制，无论是从基础理论还是工程实现方面都取得了前所未有的发展，但是依旧还有诸多问题需要解决，例如，精确的数学模型建立以及与模型相关的参数辨识、最优化飞行控制方案及控制律的设计、无人机在室内室外的定位导航与通信等［3-5］。

近年来，研究人员把一些先进控制思想和算法应用在四旋翼无人机的鲁棒控制系统中。此外，在无人机实际飞行过程中，因为长时间的飞行不可避免地会出现执行器故障，传感器失灵等问题。当这样的飞行故障出现时，如果不及时处理，会对周围人员及财产安全和无人机自身的稳定飞行造成很大威胁［6］。因此，在研究四旋翼无人机飞行的稳定性和可靠性的时候会遇到很多问题，本文主要是针对无人机提出一种控制方法，来提高无人机系统稳定性和可靠性。

由于迭代学习控制过程是利用系统的实际输出和期望输出的偏差，通过迭代学习算法寻找优化的输入信号，以使得系统的输出不断收敛于期望值［7］。迭代学习的控制过程不需要依赖动态系统的精确数学模型，就可以用非常简单的方法处理不确定、强耦合、非线性、难以建模的复杂系统。少量的先验知识就可以使迭代学习控制得以实现，并且重复运行的次数越多控制精度越高，所以本文设计的迭代学习观测器，适用于四旋翼无人机控制系统中。

本文主要是为了解决四旋翼无人机飞行的安全可靠性，首先需在设计飞行控制系统时考虑到外界的扰动和可能发生的故障，设计迭代学习观测器并设计相对应的自适应控制器，通过理论推导验证迭代学习观测器的跟踪效果，并且利用Lyapunov 稳定理论，对所设计的自适应控制率的稳定性进行分析说明。对四旋翼无人机系统的稳定性和可靠性有了进一步的提升。

1 无人机控制系统模型

四旋翼无人机外形简单、性能卓越，是一种能垂直起降的、多旋翼无人机，它在总体布局形式上属于非共轴式无人机［8］。下面是四旋翼无人机的数学模型，四旋翼无人机的结构及原理示意图如图1所示，4 个旋翼电机固联在刚性十字交叉结构支架的末端。旋翼1、3 和2、4 分别组成两组动力系统，并以相反的方向旋转，当无人机处于悬停状态时，旋翼产生的总扭矩为零。

图1 四旋翼无人机的结构及原理示意图

通过改变旋翼的转速，无人机就能实现各种动作飞行。同时增加或减小4 个旋翼的速度可产生垂直运动，以相反的方向改变旋翼2 和4 的速度，可产生滚转以及相应的侧向运动。同理，以相反的方向改变旋翼1 和3 的速度，可以产生俯仰运动和相应的纵向运动［5］。成对地改变旋翼1、3 和旋翼2、4的速度，使得两组旋翼的总扭矩不为零，就会产生偏航运动［9-11］。

将机体坐标作为参考坐标系，依据牛顿-欧拉方程，可建立描述其无人机的运动方程。将获得的非线性动态模型在工作点附近进行线性化，可获得无人机小扰动线性化方程如下：

2 迭代学习观测器及收敛性分析

2.1 四旋翼无人机系统模型2.1.1 姿态动力模型

由Newton-Euler 方程得四旋翼绕机体坐标轴的转动方程为［9］

由机体坐标系和地面坐标系之间的转换关系可得四旋翼姿态运动学方程为

2.1.2 空气动力学模型

建立力矩空气动力学模型主要是描述四旋翼所受的外力矩。四旋翼直升机在空中主要受以下力矩影响：

式中，kL为与旋翼面积、旋翼半径、空气密度等因素有关的升力系数，ωi为旋翼转速，l 为电机轴到四旋翼重心的垂直距离，kQ为反扭矩系数。旋翼的陀螺效应是指当四旋翼俯仰和滚转运动时，高速旋转的旋翼所产生的阻碍俯仰和滚转运动的附加扭矩。数学表达式为

由于所研究四旋翼飞行器的旋翼面积和转动惯量较小，且飞行速度较慢，通常可以将陀螺效应和阻力力矩忽略不计，则四旋翼所受外力矩可表示为

2.2 迭代学习观测器

设计迭代学习观测器，利用迭代学习观测器以便于实时观测系统某些参数的变化，并且能及时检测到执行器是否发生了故障。设计的观测器为：

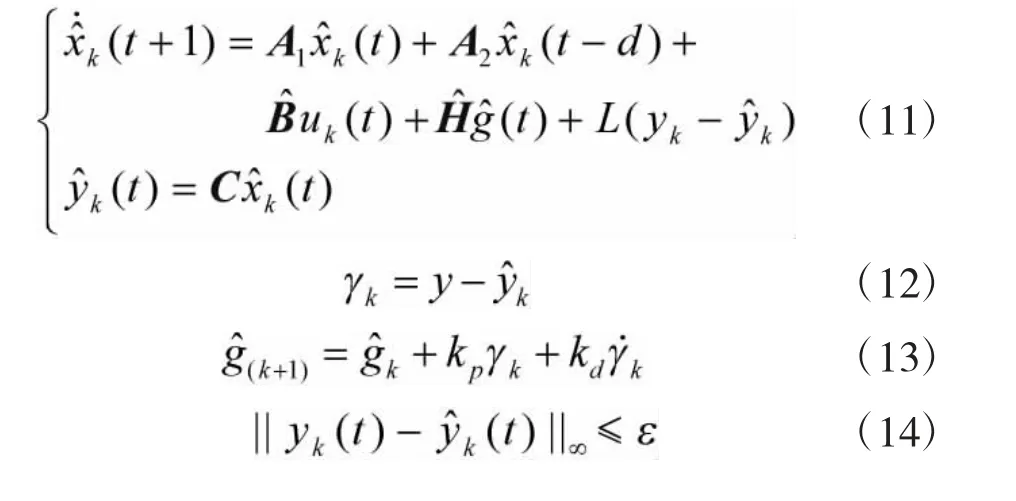
2.3 定理1 及证明

3 自适应鲁棒控制器设计

3.1 设计控制器

设计一个鲁棒自适应容错跟踪控制器，使得无人机的飞行控制系统在正常情况下和执行器故障及外部扰动情况下，渐进稳定且其自适应容错性能

ξi1、ξi2、ξi3、ηif、ηig、ηih为正常数。

定理2：考虑发生执行器故障的无人机系统模型，在定理1 成立的前提下，应用上述的控制律及参数自适应律，则可以保证发生执行器故障的无人机系统的轨迹跟踪误差仍将逐渐趋近于零。

3.2 稳定性分析

Lyapunov 函数定义为：

4 仿真研究

对式（10）所设计的四旋翼无人机系统的滚转角和俯仰角进行仿真，来验证所设计控制方法的有效性。滚转角和俯仰角期望轨迹分别为：

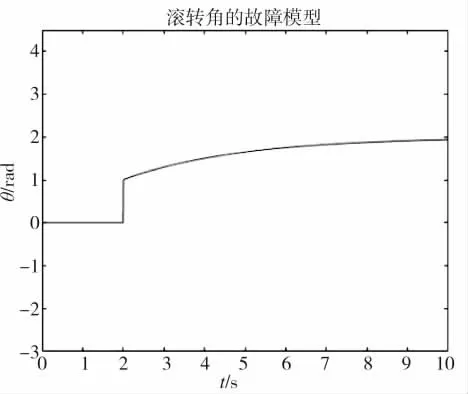
图2 滚转角的故障模型图

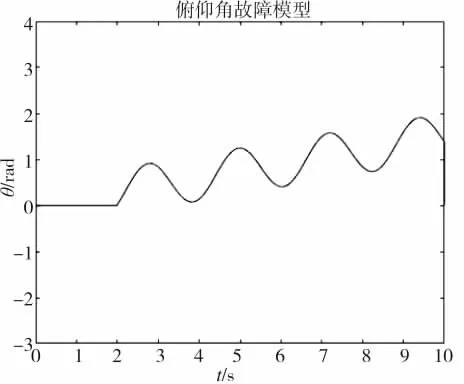
图3 俯仰角的故障模型图

采用式（12） 的控制率及自适应率，ξi1=3，ξi2=0.05，ξi3=5，ηif=0.2，ηig=0.02，ηih=0.1 并 设 定 以 下参数：

无人机的滚转角及俯仰角的容错轨迹曲线如图4～图5 所示。

图4 滚转角的容错跟踪轨迹图

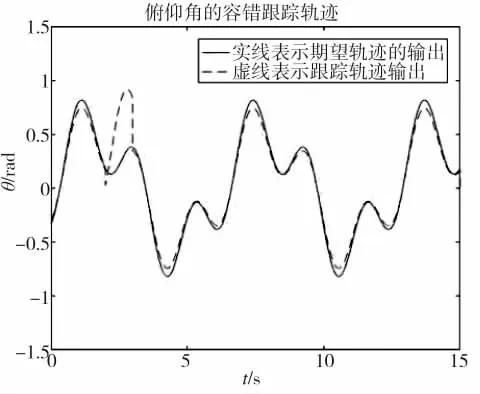
图5 俯仰角的容错跟踪轨迹图

通过图4～图5 的仿真结果可以看出，所设计的迭代学习故障跟踪观测器，能够很好地逼近所发生的执行器故障，执行器在第2 s 时发生了执行器故障，在此基础之上，应用所设计的自适应鲁棒控制器，能够实现在比较短的时间内对四旋翼无人机控制系统的容错控制，其各电机子系统发生故障的时候仍能各自跟踪其期望轨迹，增强了故障发生时的可靠性。

5 结论

本文针对发生执行器故障的无人机各电机控制系统，设计了基于迭代故障跟踪观测器的无人机控制系统的主动容错控制器。利用迭代故障观测器去观测各电机控制系统的状态，并通过迭代实时跟踪执行器故障，给出了该观测器的收敛性分析，并在此基础上设计了主动容错控制器。最后应用Lyapunov 稳定性理论，证明了所设计的容错控制器的稳定性。并且在matlab 中验证控制算法在无人机系统模型上的跟踪控制效果，可以看出本文所设计的方法具有良好的跟踪性，所以此方法具有可行性与实际应用性，能够提升四旋翼无人机系统的稳定性和可靠性。