基于HTCPN 的飞机备件需求预测方法*

2021-09-08王莉莉蔡忠义张翔宇

火力与指挥控制 2021年8期

王莉莉，邹旭，李岩，蔡忠义，张翔宇

（1.空军工程大学，西安 710051；2.解放军95746 部队，成都 611530）

0 引言

当前，新的军事训练大纲已经在部队贯彻实施，训练强度和难度较以往相比有了大幅的提高。在此背景下，飞机高强度、大载荷的使用对部队维修保障能力提出了更高的要求。飞机备件作为航空兵部队的特殊战略物资储备，是维修保障资源的重要组成部分，直接影响着装备完好率和可用度指标［1］。因此，针对航空兵部队维修保障工作，开展飞机备件需求预测工作具有重要的军事意义和研究价值。

目前，国内外学者针对备件需求预测问题进行了较为深入的研究，传统方法主要有时间序列预测法和模型解析法。基于历史数据的时间序列预测法，包括自回归移动平均法、指数平滑法、灰色预测法［4］、人工神经网络法［5］，以及基于上述方法的修正改进方法和组合预测方法［6-9］。这类方法主要通过对备件历史使用数据进行拟合，仅在历史数据充分，且备件需求波动较小的情况下适用，具有很大的局限性。并且，仅考虑时间序列作为备件需求量的影响因素，而忽视备件需求产生的其他主要因素，尽管预测模型的误差越来越小，但现实意义值得商榷。

数学模型解析法依据可靠性参数建立备件需求预测模型。例如，文献［1］中提出在满足备件保障概率下的备件定量计算模型，文献［10］提出在满足装备完好率下的备件需求量确定方法，文献［11-13］以备件保障效能指标为约束条件，以备件库存成本作为目标函数，建立多目标优化模型求解最优备件配置方案。解析法通常假设备件需求量服从泊松分布，由于实际的备件需求是在综合作用下产生的，备件需求过程并不是平稳泊松过程，在一定程度上假设不符合实际。同时，运用解析法构建出的目标优化函数较为复杂，难以得到最优解。为解决上述问题，部分学者通过计算机仿真方法开展备件需求预测工作的研究，例如文献［14］建立了基于可用度的非战斗损伤抢修备件需求量模型，采用Monte-Carlo 算法对模型进行仿真分析和计算。文献［15］建立了飞机后续备件供应保障系统的Petri 网模型，运用面向对象的数字仿真手段进行备件预测。尽管上述方法减少了部分不合理假设，克服了时间序列预测法的缺点，但在仿真过程中仍存在维修保障过程过于简化，仿真时钟推进机制不合理等不足，降低了仿真方法的准确性。

1 分层赋时着色Petri 网基本理论

HTCPN 融合了层次Petri 网［16］、赋时Petri 网［17］和着色Petri 网［18］的特点，是对Petri 网的综合扩展。其中，分层技术解决了构建复杂模型时的空间爆炸问题；着色令牌有利于数据结构的合理规划；时间戳可以准确描述系统部件之间的时序关系，使库所和变迁具有时间属性。基于上述特点，HTCPN能够清晰、有效地描述复杂离散的动态系统，可用于解决备件保障活动中模型结构复杂、时间节点繁多且涉及对象广泛等问题。

定义1 HTCPN 系统可定义为一个九元组：N={P，T，A，V，D，C，R，I，S}。其中：

1）P 为库所（Place）的有限集合，具体表示为P={pi|i=1，2，…，n}，可分为输入库所和输出库所。

2）T 为变迁（Transition）的有限集合，含有3 个子集：Ta，Tb，Tc。其中，Ta={t1，t2，…，tk}为瞬时变迁集合，Tb={tk+1，tk+2，…，tm}为延时变迁集合，Tc={tm+1，tm+2，…，tn}为子网变迁集合。子集相互独立且满足以下条件：

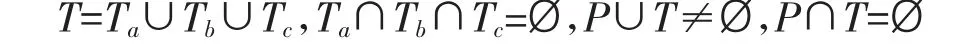
3）A 为弧（Arc）的有限集合，包括变迁输入弧、变迁输出弧以及变迁双向弧，弧只能连接库所与变迁，不能直接将库所（变迁）与库所（变迁）相连，满足A⊆（P×T）∪（T×P）。

4）V：P→N+∞为库所容量函数，表示P 中可以容纳的令牌数量。

5）D 为时间延迟函数，定义在P 或T 上。对于定义在库所上的时间延迟函数，在变迁触发后，需经历延迟时间D（p），进入输出库所p 的令牌才可触发；对于定义在变迁上的时间延迟函数，在变迁t 触发后，需经历延迟时间D（t），才可使输入库所中对应的令牌进入到输出库所。另外，时间延迟函数可根据实际情况，定义为常量或随机变量。

6）C 为颜色函数，可对库所中的令牌进行着色标记以区分不同类型。

7）R 为识别函数，定义在变迁上，表示变迁触发的满足条件。

8）I 为初始化函数，定义在库所上，表示库所初始状态，包括令牌数量和颜色类别。

9）S 为抑制弧的集合，一个抑制弧包括起始端和终止端，表示当起始端所连库所状态变化时，抑制终止端所连库所状态变化，且满足S∪P×T。

2 基于HTCPN 的飞机备件保障过程仿真

飞机维修保障工作主要包括资源保障工作、故障维修工作以及周期性工作。其中，资源保障工作包括飞行前准备、再次出动准备以及飞行后检查。故障维修工作主要是飞机发生故障后的修复性维修工作。周期性工作主要是飞机的定期检查。

飞机备件需求的产生主要来源于故障维修工作，所以，本文通过构建飞机的维修保障工作HTCPN 仿真模型，对备件需求进行预测。由于构成飞机整体的分系统较多，且部分分系统故障发生概率较小，为简化模型，本文在构建故障维修工作模型时选取主要发生的3 种典型分系统故障。同理，选取分系统下的典型备件故障，构建分系统故障维修工作模型。

2.1 飞机备件保障资源实体化模型

根据定义1，在运用CPN Tools 软件构建HTCPN 模型进行仿真前，需要对飞机备件保障资源进行实体化描述。实体化模型的参数包括飞机型号、编号和数量，备件的种类、编号和数量等。备件可分为可修备件和不可修备件，又可分为现场可更换单元（LRU）、内场可更换单元（SRU）。本文将系统边界限定在基层级维修，不考虑内场可更换单元的使用情况。

通过实体化描述，建立飞机库所和备件保障资源库所，库所中的令牌代表库所内含有的飞机或各类备件保障资源，不同颜色的令牌表示不同的实体类型。如图1 所示，在CPN Tolls 软件中的模型化表示如图2 所示。

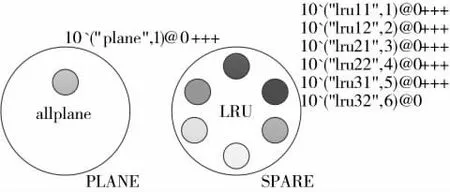
图1 实体化模型

图2 中飞机库所具有某型飞机10 架，备件（LRU）资源库所具有6 种不同类型的备件各10个。在进行案例建模和仿真时，可根据实际情况，改变库所中飞机、备件的型号（种类）和数量。HTCPN模型在仿真运行时，代表各类实体资源的着色令牌，将根据库所、弧以及变迁的触发条件进行转移，模拟备件资源在飞机维修保障工作中的动态使用过程。

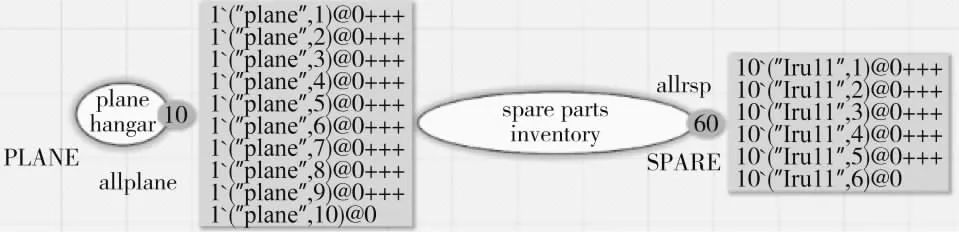
图2 CPN Tools 软件中实体化模型

2.2 飞机维修保障工作HTCPN 总网仿真模型

假设初始时刻所有飞机停留在飞机库所中，且均处于完好状态。根据仿真时间推进，库所中的飞机在执行任务前要进行飞行前准备工作，在准备工作结束后，准备进入机场跑道进行起飞前滑行。模型中通过一个抑制弧禁止跑道上同时进行飞机的起飞和着陆工作，使仿真模型更贴近实际。飞机在飞行后进行故障检测，若飞机出现故障，则该飞机进入故障维修仿真模块，并判定故障位置，通过更换备件的方式排除故障；若无故障，则飞机进入资源保障工作模块，由于本文研究重点为备件需求预测方法，所以这里对资源保障工作进行模型简化，用其他资源保障工作模块进行替代。基于上述过程分析，按照时间先后顺序进行仿真。飞机维修保障工作HTCPN总网仿真模型的构建如图3 所示。

图3 维修保障工作HTCPN 总网仿真模型

2.3 故障维修工作HTCPN 子网仿真模型

针对总网仿真模型中的故障维修工作（corrective maintenance），构建第二层子网仿真模型，如下页图4 所示。

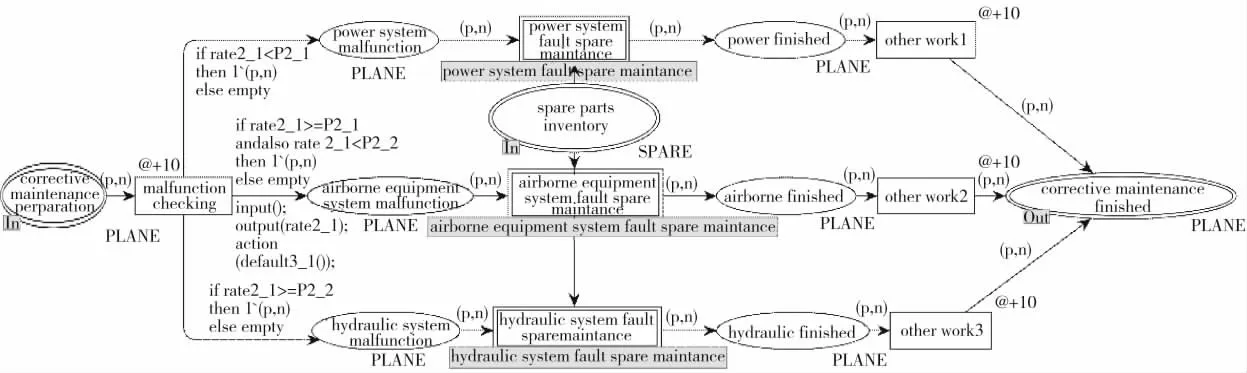
图4 故障维修工作HTCPN 仿真模型

在排除人为因素和环境因素的影响下，飞机的可靠性指标是飞机故障的主要影响因素。因此，本文根据飞机各部件的可靠性指标，结合仿真时间周期，确定飞机、分系统，以及分系统下零部件的故障概率。结合部队实际故障统计数据，本文选取故障发生次数较多、对飞机任务成功率影响较大的3 种机载分系统进行研究，其中包括动力分系统、机载设备分系统和液压分系统。

2.4 分系统故障维修工作HTCPN 子网仿真模型

由于3 种分系统下涉及的备件种类和特性不同，所以需要构建分系统故障维修工作子网仿真模型，即第3 层子网仿真模型，以动力分系统为例，如图5 所示。

图5 动力分系统故障维修工作HTCPN 仿真模型

在计算仿真模型中的故障概率之前，首先要对飞机的飞行时间进行折算。因为仿真模型的时钟推进不仅包括飞机的飞行时间，同时也包括维修保障工作的时间。针对仿真周期内总飞行时间存在的误差，本文对其进行换算，可近似表示为：

其中，T 表示仿真周期时间，t1表示单次飞行计划的飞行时间，t2表示单次飞行计划所需的维修保障的总平均工卡工时。

对于备件的可靠性参数，不可修备件的平均无故障工作时间，可参照实际使用的统计数据或厂家提供的备件参数列表。对于可修备件的平均寿命，由于实际维修时间远小于备件使用时间，可忽略维修时间，将可修备件的平均寿命等效为不可修备件的平均无故障工作时间进行处理。

假设可修备件的平均故障间隔时间为MTBF，故障后的维修率为η，在不考虑维修时间的条件下，其在仿真周期内的平均寿命可等效为不可修备件的平均无故障时间MTBF'。

对于备件故障发生的规律，本文假设备件故障规律服从指数分布或威布尔分布，参照GJB 4355-2002，确定各备件在仿真周期内的平均故障概率。

1）指数分布

电子件的寿命分布一般服从指数分布，若已知平均无故障工作时间为MTBFi，则该类型备件在仿真周期内的平均故障概率为：

其中，T1表示单次飞行小时数。

2）Weibull（威布尔）分布

机电件的寿命分布一般服从Weibull 分布，若已知备件平均无故障工作时间为MTBFk，形状参数β，则该类型备件在仿真周期内的平均故障概率为：

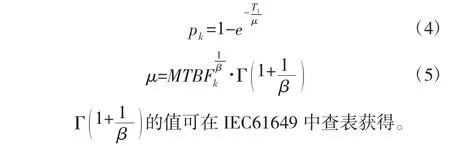
在实际情况中，两个或两个以上备件故障同时发生的情况较少，所以本文假设备件故障发生事件相互独立，且在仿真周期内任意两个备件不同时发生故障，结合各备件的平均故障概率，分别计算飞机动力分系统、机载设备分系统和液压分系统发生故障的概率ppower、pequip、phydra。

假设飞机动力分系统中有n 个备件，且已知每个备件的平均故障概率pi（i，j=1，2，…，n），则动力分系统发生故障的概率为：

基于上式，可以得到p'equip、p'hydra。

同理，在进入动力分系统故障维修模块时，各备件发生故障的概率近似为：

最后，以p'power、p'equip、p'hydra、p'i作为故障模块前的判定标准进行模型仿真。

运用CPN Tools 对上述模型进行仿真时，飞机库所和备件库所中的令牌在仿真时钟的推进下进行转移，“@+”代表令牌的时间戳，在延时函数作用下，“@+”会随之增加，同时CPN Tools 界面中会显示仿真运行时间（Time）以及仿真步骤（Step）。

3 飞机备件需求预测模型

为了衡量备件需求量配置方案的实际效果，本文引入飞机出动架次率作为验证指标。依据验证指标，构建基于飞机出动架次率的备件需求预测模型，通过调整备件数量并计算对应的飞机出动架次率。提出备件需求量确定规则，求解最优配置方案。

3.1 飞机出动架次率

飞机出动架次率（SGR）是指在单位时间内飞机能够出动的次数，也称为单机出动率或战斗出动强度，是衡量战机在任务环境下连续出动能力的重要指标，也是反映航空兵部队战斗力的重要参数［19］。其计算公式为

其中，NSG为仿真周期时间内飞机出动架次数，对应总网中“take off”变迁的触发次数。N 是飞机数量。

3.2 飞机备件需求量确定规则

不同的备件需求量配置方案下，通过仿真得到的飞机出动架次率不同。若备件数量不足，可能会导致飞机在故障维修模块中的“waiting LRU”库所中停留，从而降低飞机出动架次数。若备件需求量远大于实际所需，即飞机不会出现等件、缺件情况，此时，继续增加备件需求量对飞机出动架次数影响很小，但造成了备件资源的浪费。因此，本文在HTCPN模型的基础上，以飞机出动架次率为验证指标，建立备件需求量确定模型，求解在保证最大飞机出动架次率下的备件配置方案。件需求量Mi=j。其中，ε 为范围在（0，1）内的判定阈值，一般结合实际情况确定。根据备件需求量确定规则，分析与不同备件数量的变化关系，即可得到在保证最大出动架次率下的最小备件需求量。

图6 Rij 与备件需求量关系求解流程

4 算例分析

4.1 参数设定

假设某航空兵部队有8 架同型号飞机在位。已知该型号飞机的装备层次结构如图7 所示。系统中LRU 的相关参数如表1 所示。

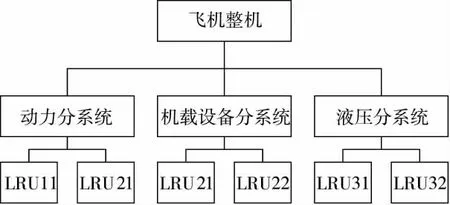
图7 某型飞机装备层次结构图

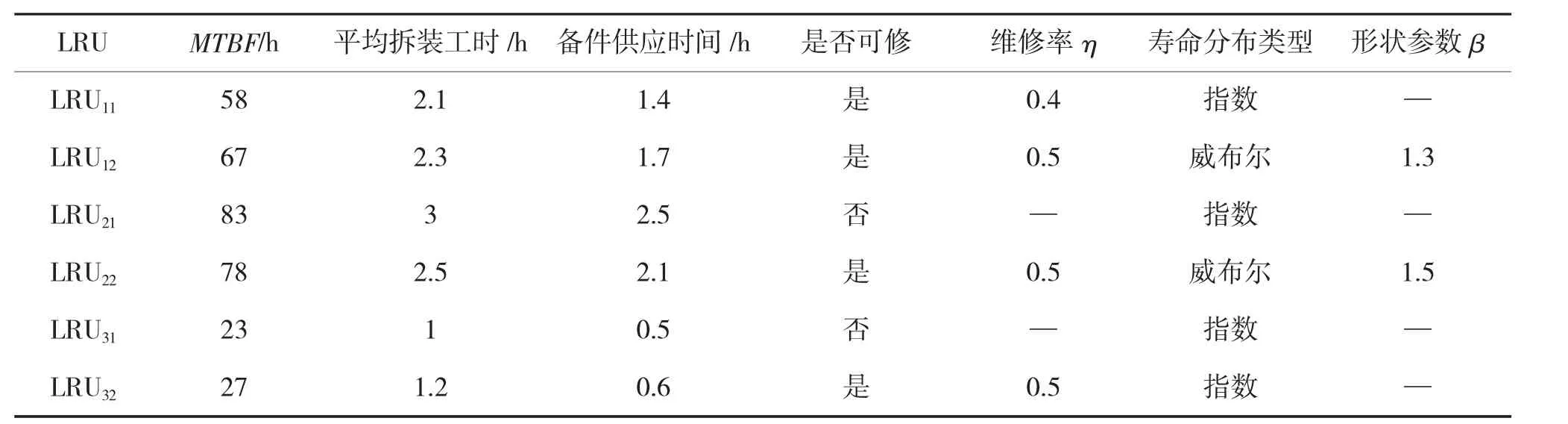
表1 LRU 相关参数

其次，根据式（1）进行飞行小时仿真时钟折算，可得该周期内单架飞机总飞行小时T'为136 h。再次，由式（2）可得可修备件等效后的MTBF'值，修正后MTBF 的如表2 所示。

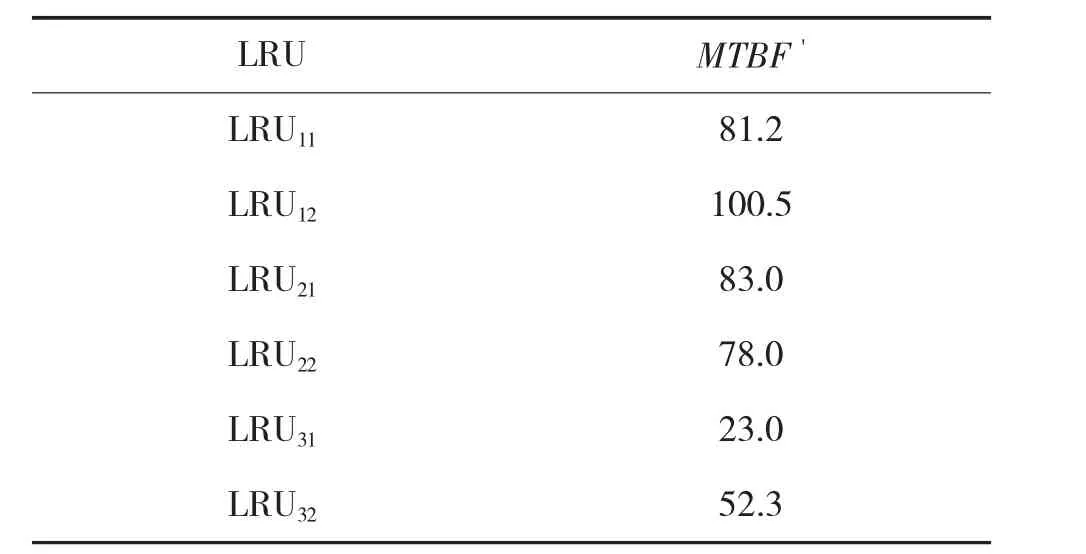
表2 等效后的备件MTBF '

最后，根据不同寿命分布类型备件的故障规律和参数，结合Bayes 公式，由式（3）～式（10），确定在仿真周期内故障对象的故障概率或条件概率，如下页表3 所示。

表3 仿真周期内的故障概率

4.2 结果确定

将参数输入到本文模型中，进行500 次仿真后得到与各类备件需求量的对应关系，如下页图8 所示。设定判定阈值ε 取0.01，结合备件需求量确定规则对数据进行分析计算，得到最优备件配置方案为LRU11配置8 个，LRU12配置13 个，LRU21配置9个，LRU22配置18 个，LRU31配置20 个，LRU32配置11 个。

图8 Rij 与备件数量关系图

4.3 对比验证

为验证本文方法的科学性和优越性，设定2 个对比方案，其中，方案1 是所有备件均充足时的配置方案，方案2 是以文献［10］方法得到的备件配置方案。配置方案如表4 所示。

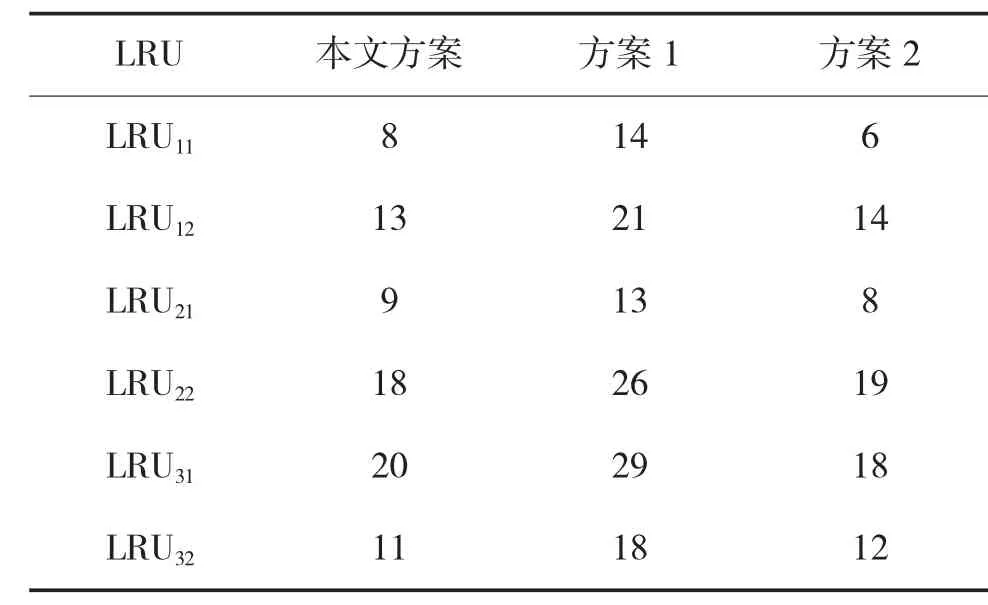
表4 备件需求量配置方案

将各方案的备件需求量输入仿真模型中，进行500 次仿真，得到的对比结果如表5 所示。

由表5 可知，本文方案的平均飞机出动架次率与方案1 的平均飞机出动架次率仅差1.3%，但本文方案的备件数量配置规模相比于方案1，缩减了37.1%，在假设备件成本相同的情况下，有效降低了备件库存管理成本，提高了备件保障费效比。本文方案与文献［10］给出的方案相比，在备件配置规模大体相同的情况下，本文方案的飞机出动架次率相较于方案2 增加了1.1%。对比结果验证了本文方法的科学性和有效性。