基于MacCormack 法的膨胀波火炮内弹道数值模拟*

郭张霞，谢景云，李 闯，王永存，金寅翔

（1.中北大学机电工程学院，太原 030051；2.晋西工业集团有限责任公司，太原 030024；3.西北机电工程研究所，陕西 咸阳 712099）

0 引言

膨胀波火炮采用新的发射机理研制而成，在内弹道的某一时刻，突然打开安装在炮尾处的后喷装置，膛内部分高温高压燃气从喷管向后喷出，膛底压力下降，膨胀波向炮口方向移动，追赶向前运动的弹丸，使膨胀波在弹丸飞出炮口前未赶上弹丸，便能够在不降低火炮威力的情况下，显著减小发射过程中产生的后坐能量和身管热量［1-3］。

内弹道设计是膨胀波火炮研制的基础。膨胀波火炮内弹道模型基于闭膛经典内弹道，增加关于流量的方程，在进行求解计算时，会假设平均压力求解、弹后空间密度均匀分布，这样会引起压力呈现整体性变化，计算出的弹丸初速比实际结果低，对火药燃气后喷产生的膨胀波在炮膛的传递过程，经典内弹道不能进行准确描述，后喷过程中火药燃气在膛内的流动规律无法准确获得。膨胀波在膛内的流动是一维的，而膛内火药燃气的流动也主要为一维，为准确、方便地计算弹丸初速，获得膛内流动参数的变化规律，创建膨胀波火炮一维均相流内弹道模型。一维均相流模型忽略气固两相间的相互作用，计算相对简单、便利，求解结果具有相当的准确性，能满足工程上的需要，是研究膨胀波火炮内弹道一个较好的工具［4-7］。

MacCormack 法是Lax-Wendroff 的变种，在空间和时间上具有二阶精度，是解决流体流动问题的一种显式有限差分法，具有简单、便于理解和易于编程实现、占用电脑内存小、求解时间短等优点，常用于求解可压缩和不可压缩流体非定常流动，往往都能得到令人满意的求解结果，该方法在兵器装备、航空航天、管道模拟等方面均有广泛应用［8-11］。

本文建立了膨胀波火炮的一维均相流模型，并采用MacCormack 法，推导出膨胀波火炮的一维均相流方程，并对其进行内弹道求解，得出膨胀波火炮的平均压力、弹丸速度等参数，通过与经典内弹道求得的结果进行对比，证明了MacCormack 模型的正确性。

1 膨胀波火炮一维均相流数学模型

1.1 基本假设

根据膨胀波火炮的发射特点，对其进行以下假设：

1）气体和固体混合均匀，将混合体看作连续介质的流体，忽略气相和固相间的相互作用；

2）混合体在膛内一维流动，不考虑混合体流动时的摩擦力；

3）火药颗粒服从几何和指数燃烧定律，所有的火药颗粒的形状、大小和物化性质均相同；

4）通过减少火药力的办法来修正身管的热散失和未燃火药由初温升到着火点温度而吸收的热量；5）不考虑身管后坐对膛内混合体流动影响；6）气体压力视为混合体的压力。

1.2 膨胀波火炮内弹道

火药燃气的状态方程为

1.3 计算参数

笔者以35 mm 闭膛火炮为计算原型，后喷装置打开方式选择为主动式爆炸隔板打开，（下文称“开闩”）假设开闩瞬间完成，所需的身管结构参数、火药参数等如下表1 所示。

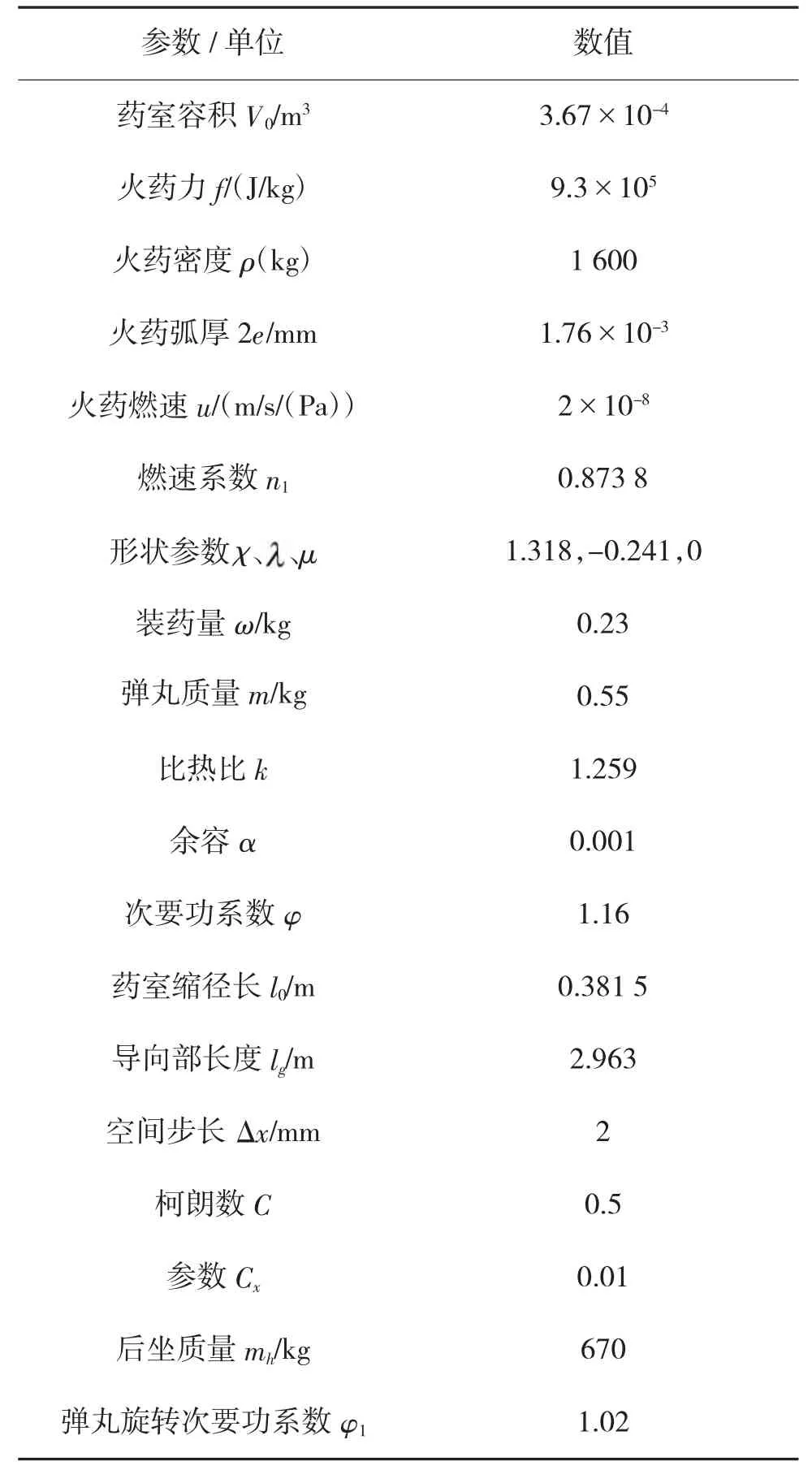
表1 35 mm 膨胀波火炮计算参数

图1 膨胀波火炮炮膛结构

其中，截面A 为喷管出口，截面B 为喷管入口，截面C 为药室底面，截面D 是弹底面（弹丸未运动前），截面E 为炮口端面，其结构参数如表2 所示。

表2 炮膛结构参数

后喷装置最佳打开时间为：开闩后，膨胀波逐步向炮口方向的运动，在弹丸出炮口的瞬间，膨胀波刚好传递到弹底，此为最理想状态，不影响弹丸初速，并能有效降低后坐力。开闩时间过早，会影响弹丸初速，开闩时间过迟，后喷气体减少，减后坐效率降低。根据闭膛经典内弹道，可以反推出膨胀波火炮的最佳开闩时间，为2.27 ms。

2 膨胀波火炮MacCormack 内弹道模型

2.1 MacCormack 法解内弹道方程组

采用MacCormack 法求解膨胀波火炮一维均相流内弹道，称为MacCormack 内弹道模型，MacCormack 法由预估步和校正步构成。

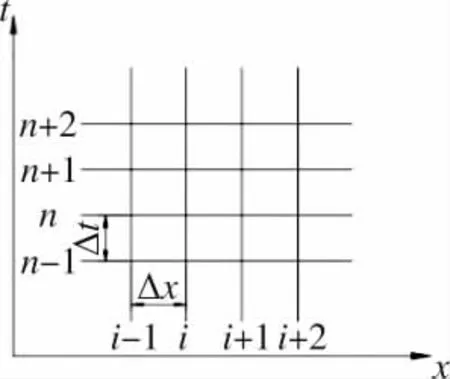
图2 时间推进

预估步为：

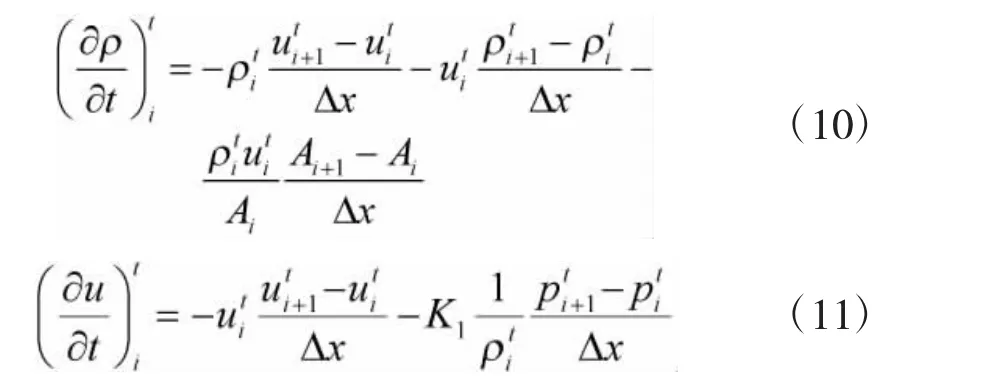
2.2 边界条件

2.2.1 左边界

左边是炮尾方向，左边求解分以下3 种情况：1）固定壁面；2）超声速出口；3）亚声速出口。判断条件为：1）后喷装置未打开，按固定壁面求解，后喷装置打开；2）喷管尾部马赫数Ma≥1，按超声速出口求解；3）喷管尾部马赫数Ma≤1，按亚声速出口求解。

2.2.2 右边界

右边是炮尾方向，右边求解分以下3 种情况：1）运动壁面；2）超声速出口；3）亚声速出口。判断条件为：1）弹底截面未离开炮口截面，按运动壁面求解，弹底截面离开炮口截面；2）炮口马赫数Ma≥1，按超声速出口求解；3）炮口马赫数Ma≤1，按亚声速出口求解。

其中，Cx是任意给定的参数，在0.01 到0.03 之间取值，用于调整计算。

3 MacCormack 内弹道模型计算结果

3.1 验证MacCormack 内弹道模型

根据MacCormack 内弹道模型，在MATLAB 软件中编写内弹道程序，计算出不开闩和开闩状态下的内弹道参数变化规律，并与闭膛经典火炮内弹道计算结果，以及用平均压力法计算的膨胀波火炮内弹道结果进行对比，对比结果如下页图3（a）～图3（d）和表3～表4 所示（图表中方法1 为MacCormack法，方法2 为平均压力法）。

图3 平均压力与弹丸速度变化曲线图

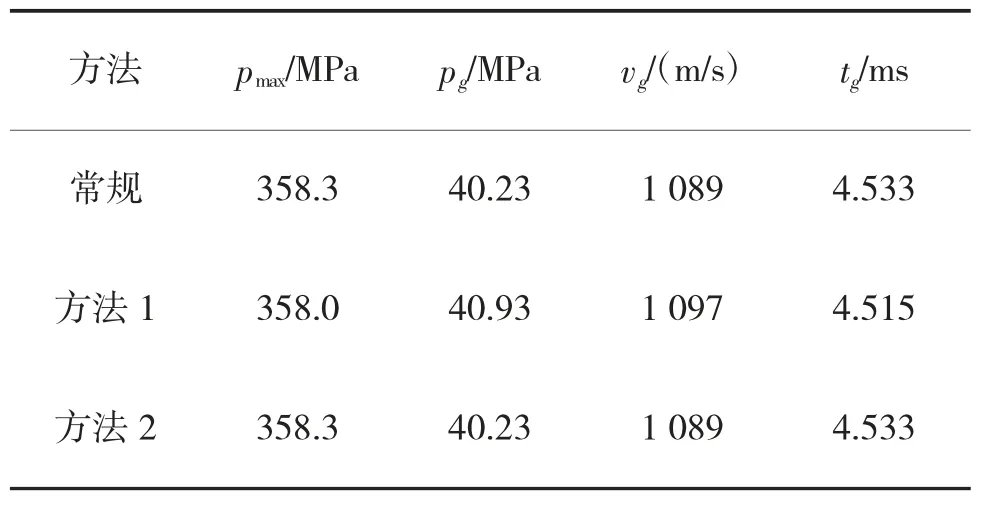
表3 内弹道特殊点数据对比（不开闩）

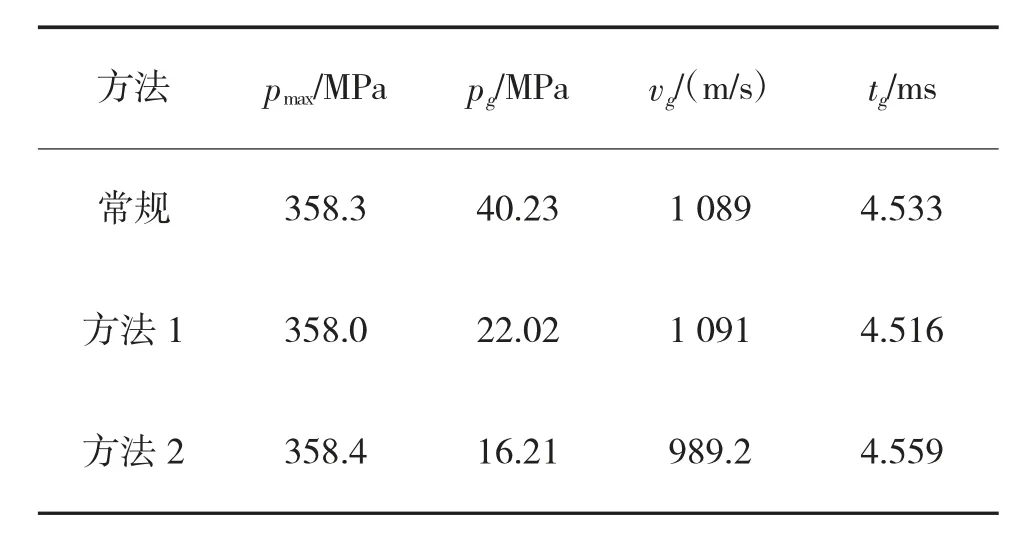
表4 内弹道特殊点数据对比（开闩）

如图3（a）～图3（b），在不开闩情况下，MacCormack 法和平均压力法求解的膨胀波内弹道参数变化规律与闭膛经典火炮一致；如图3（c）～图3（d），在开闩情况下，平均压力法计算的弹丸初速与闭膛经典内弹道初速相差较大，而MacCormack 法所求弹丸初速与闭膛经典内弹道初速相近，满足膨胀波火炮的发射要求。通过上述对比，证明了MacCormack 内弹道模型的正确性，并且比平均压力法求解结果更准确。

3.2 MacCormack 内弹道模型求解结果

本节用MacCormack 法求解膨胀波火炮内弹道，开闩和不开闩情况的内弹道参数对比结果如图4（a）～图4（d）所示，部分点的数据对比如表4～表5所示。

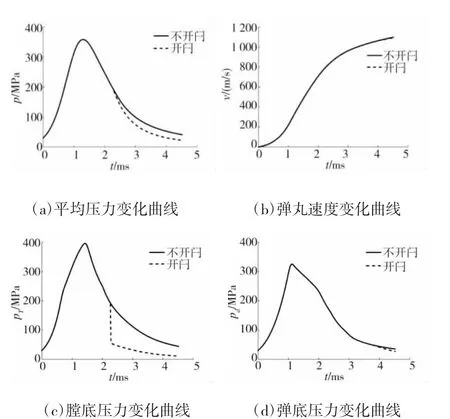
图4 内弹道参数对比结果

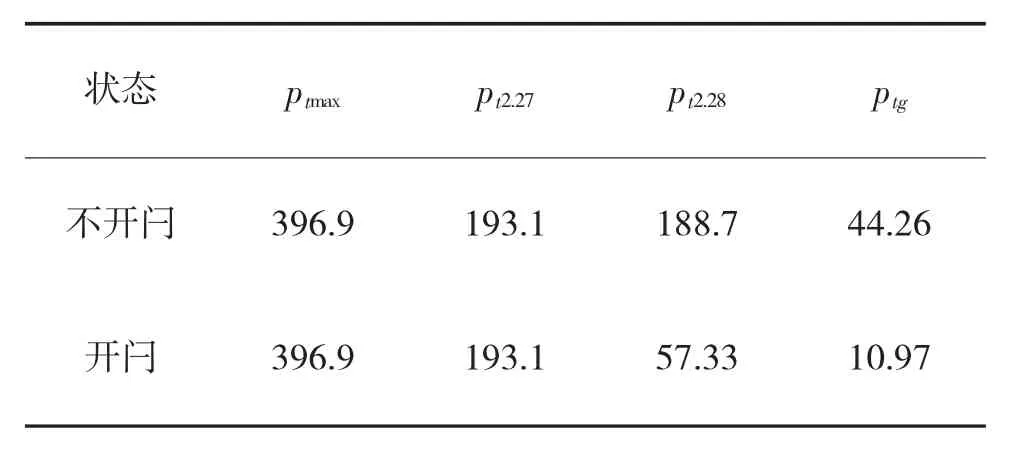
表5 膛底压力结果对比（单位：MPa）

（下标“d”表示弹底，“t”表示膛底，“g”为出炮口点，“max”表示最大值，数字表示特殊时间点）

图4 和表4～表6 表明，运用MacCormack 内弹道模型计算膨胀波火炮内弹道，弹丸初速在开闩和不开闩状态下差别很小，开闩与否几乎不影响弹丸初速；开闩后，膛内压力减小，膛底压力在开闩后的零点几个毫秒内迅速降低，而后继续减小；弹底压力在刚开闩时并无影响，在3.8 ms 左右，开始略有下降，可能是膨胀波传递到弹底，也可能是求解误差所致，并且在出炮口时弹底压力差值不大。

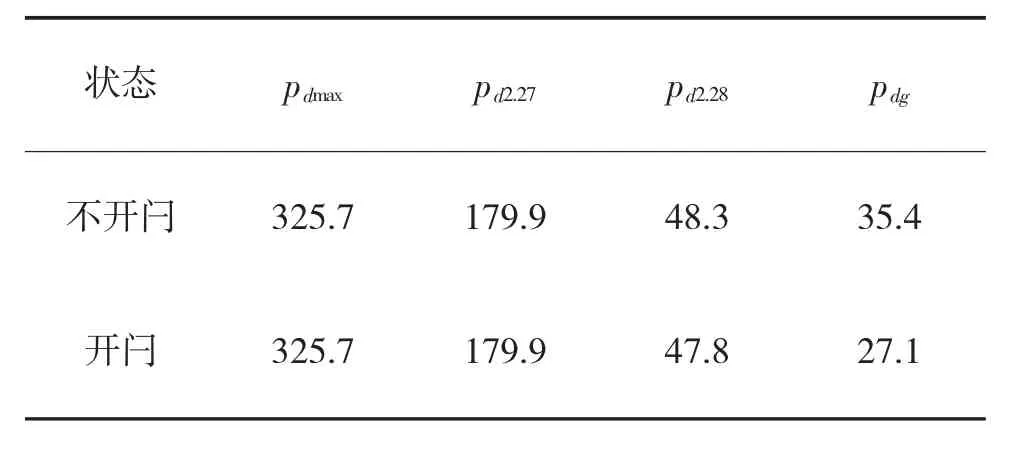
表6 弹底压力结果对比（单位：MPa）

根据计算结果，得出最大压力附近时刻到出炮口时间段的膛内火药气体压力、速度、密度、温度等内弹道参量的分布规律，如图5 所示。

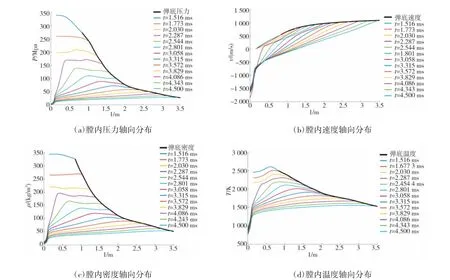
图5 内弹道参数分布规律图

如图5（a）所示，彩色曲线为不同时刻的膛内压力的轴向分布，把彩线右端的点连接起来而绘制的黑色曲线，为弹底压力随时间的变化规律，图5（b）～图5（d）中曲线类似。由图5 可知，在开闩前，最大膛压出现在药室底部附近；开闩后，最大膛压向炮口方向移动，火药气体一部分向后喷出，药室底部速度与炮口方向相反，膛内火药气体的密度、温度变化规律与压力的一致。

4 结论

本文建立了膨胀波火炮内弹道一维均相流模型，并推导出适应MacCormack 格式的数值求解模型，对膨胀波火炮内弹道进行数值仿真，并将计算结果与闭膛经典内弹道结果进行对比，验证了所建模型的正确性。计算得到了不同时刻下，膨胀波火炮膛内压力、速度、密度、温度的分布规律，真实地反映了膨胀波在膛内的运动过程。