基于结构可置信性鲁棒优化算法的离散优化问题研究

23232323

(1.大连大学 机械工程学院，大连 116622； 2.大连理工大学 工业装备国家重点实验室 工程力学系，大连 116024；3.大连理工大学 宁波研究院，宁波 315016)

1 引 言

结构优化设计按照设计变量类型可以分为连续变量优化设计和离散变量优化设计。而实际上，大多数工程设计对应于离散变量优化设计问题。因为许多工程构件的选择都遵循一套标准化的计量办法，以满足工业化大生产的要求；同时测量工具通常也具有特定精度和量程，因而导致工程结构的参数通常是离散的。相对于连续优化的理论，离散优化理论的发展还处于远不成熟的阶段[1,2]。当前在处理实际工程的离散变量设计问题时，出现了两种不同的思路。一种首先采用连续优化方法得到一组最优解，然后对解的每个分量采用四舍五入或者向上取整等方法得到离散解，并凭工程师的经验对其进行适当调整和验证，以满足产品设计的需求。另一种做法是直接根据离散数学及其相关优化算法，基于严谨的理论分析和数值计算来求得工程设计问题的离散最优解。尽管现阶段来说，后种做法的计算量较大且可解决的问题也相对有限，但此类基于理性的研究方法对完善结构优化体系和指导工程设计均具有重要意义。

根据研究问题的角度不同，离散优化设计的分类方法有多种，如隋允康等[3]把离散变量优化方法分为圆整方法、离散方法和离散优化映射为连续优化的方法。Arora等[4]对非线性离散变量优化问题相关工作进行了总结。陈立周[5]撰写了国内关于结构离散优化方面较早的专著。柴山等[6]提出了精确的启发式算法，即相对差商法，能够解决目标函数和约束函数单调的离散优化问题。Templeman等[7]通过构造力学模型使离散变量问题映射为连续变量问题，予以求解后反演回离散变量问题的解。李兴斯等[8]把离散变量结构优化设计问题转化为带有互补约束的优化问题，并利用NCP函数进行求解。谭涛[9]介绍了离散变量优化设计的连续化方法。石连拴等[10]提出了离散变量结构优化设计序列定界组合算法。王跃方等[11]研究了多工况下受应力和位移约束的离散截面变量桁架结构的布局优化问题。Juang等[12]采用修正的离散拉格朗日搜索法解决了桁架结构的离散优化问题。Wolkowicz等[13]采用半定规划方法来求解离散优化问题和矩阵完成问题。此外，Bertsimas等[14]提出了鲁棒离散优化(RDO)理论，利用整数规划方法考虑了概率边界，并主要用于求解网络流问题。

另一方面，传统优化设计的研究通常认为问题的参数(如材料属性和外载荷等)是确定的，可以精确给出。但在实际应用中参数的不确定性是无法避免的，如产品制造或者测量时都可能引入系统误差和人工误差。更值得注意的是，某些优化问题可能对参数的波动具有非常高的灵敏度[15]。因而随着计算技术的快速发展，考虑不确定性的结构优化设计近年来受到越来越多的关注，相关数值优化方法大量涌现。一般来说这些方法分为两类，一类是基于概率模型，另一种则基于非概率模型。由于获得不确定性参数的概率分布函数需要较大的样本，并且研究发现概率模型对其自身的参数(如均值和方差等)较为敏感，采用非概率模型解决不确定性结构优化问题受到了广泛关注。

在非概率框架下，不确定参数通常假定为未知但有界的集合，而无需具体的参数概率分布信息。鲁棒优化的研究目标之一为在不确定框架下寻找一个最优解，使得不确定性参数在给定集合中取任何值都能满足约束条件，也称为最不利情况的设计和优化WCDO(Worst Case Design and Optimization)。非概率不确定性优化在数学规划领域的研究开始于Ben-Tal等[16-18]以及El Ghaoui等[19,20]的开创性工作。随着解决凸优化问题的内点法(特别是半定规划)的快速发展[21]，已发展出大量的理论研究成果和技术工具用来求解凸优化问题的鲁棒最优解。Ben-Tal等[22]系统地研究了鲁棒优化中的线性规划、锥规划和半定规划问题。Calafiore等[23]发展了计算不确定线性方程组的最小定界椭球法。作为不确定性分析的强大工具，区间代数通常用于WCDO问题的求解。Chen等[24]提出了区间优化方法用于不确定结构的分析，通过结合泰勒展开技术的区间扩充运算，导出了一个确定性问题的列式。近来，Guo等[25]应用区间分析中估算不确定性结构响应的界限，进而构造了鲁棒设计列式。除了区间模型外，基于椭球凸模型的鲁棒优化设计问题也受到了学者们的广泛关注[26-29]。

综上所述，离散优化问题和非概率不确定优化问题的研究方法存在较大差异。若把其割裂开来，如单纯考虑结构不确定性，所得到的最优设计(如件的横截面积)将很难找到相匹配的工业型材，而相近型材对应设计的可行性以及鲁棒性难以有效保证。而若单纯考虑结构设计变量的离散性，得到的最优设计的安全性和鲁棒性又是未知的。本文研究发现若把结构鲁棒优化的不确定参数看作未知且有界，则其求解方法和离散优化问题的求解方法则具有相似性；进而提出了基于结构可置信性鲁棒优化算法的离散优化问题求解新思路，称为鲁棒圆整法，能够解决同时考虑参数不确定性和离散性的结构离散鲁棒优化问题，保证其最优解取离散值且在不确定性的情况下仍然能够满足约束条件，从而更好地应用于解决工程实际问题。

2 求解离散优化问题的鲁棒圆整法

事实上，鲁棒优化的基本思想和传统连续优化圆整法之间存在着内在的联系。首先如图1所示，A,B,C和D四点都在连续最优解附近，都可能选为圆整后的离散最优解，但是其中最为接近连续最优解的点A却是违反约束的不可行点(如桁架面积的连续最优解经过圆整以后引起了内力重分布，对位移函数和目标函数都有影响)，圆整解的可行性无法得到理论上的保证。由于工程实际问题会尽量避免可行性无法得到保证的最优设计，而通常允许设计值存在一定的安全裕度，因此有必要对传统连续优化圆整法做出改进，使得经过圆整后的最优解能够在理论上自然满足约束条件。

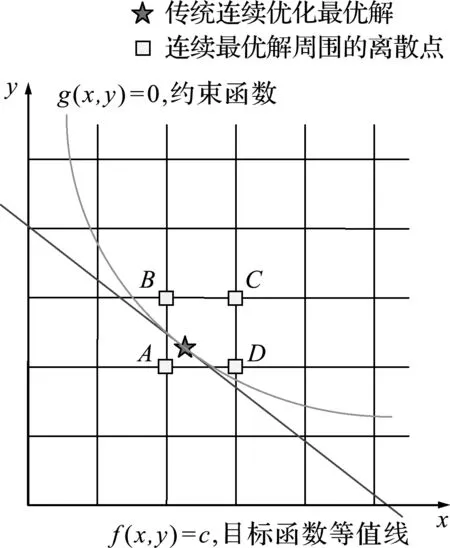
图1 传统连续优化圆整法

为了实现这一目标，可以首先在连续优化阶段构造鲁棒优化问题并采用可置信性鲁棒优化方法得到最优解，然后对该解在其鲁棒性允许的区间内进行圆整得到离散的最优解，本文把这样的方法称为鲁棒圆整法。

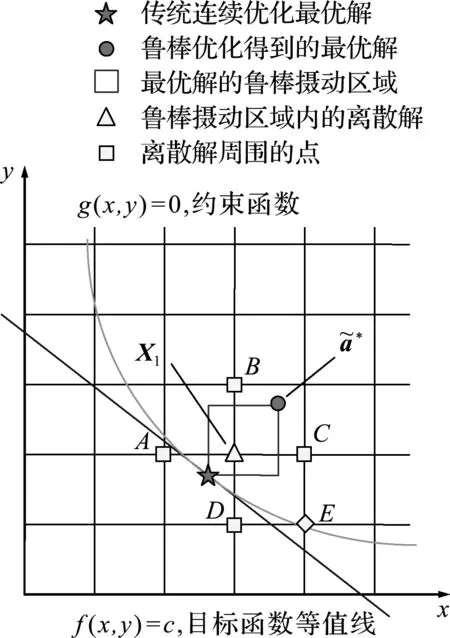
图2 鲁棒圆整法(一)

2.1 离散优化问题的等价鲁棒优化列式

鲁棒圆整法的目的和传统的连续优化圆整法一样，都是要求解离散优化问题。本文以桁架结构重量极小化问题为例，确定性离散优化问题的整数规划列式如下，

(1)

现在构造以下鲁棒优化问题，

(2)

2.2 鲁棒优化列式的求解

(3)

(4)

不确定区间是非对称的，需要进行转换，由于

(-1≤ξi≤1)

令

(5)

(6)

式中ξ=(pT,1)T∈Rnm +1

(7)

(8)

等价于

(9)

(10)

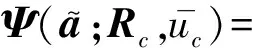
(11)

其他的结构响应约束(如应力)可以采用完全类似的方法来处理。

(12)

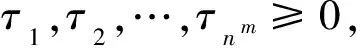
(13)

基于以上分析和讨论，原优化问题转化为如下可置信性的单层优化列式,

τi≥0 (i=1,…,nm)

(14)

2.3 离散可行解的修正

为求解离散优化问题，2.2节通过可置信性鲁棒优化以及鲁棒圆整找到了一个能够自然满足约束条件的离散可行解X1，X1是鲁棒性区域内唯一的离散点，本文对其最优性进行讨论。

首先对一阶离散局部最优解进行定义，从鲁棒圆整得到的离散可行解X1出发，每次只改变一个分量，移动到相邻的离散点处，如图2和图3所示，二维问题共有4个相邻点，分别是A,B,C和D四点，如果不存在满足约束且比X1处目标函数更小的离散解，那么就称X1为一阶离散局部最优解。

图3 鲁棒圆整法(二)

本文利用相对灵敏度商的规则或者相对差商规则[6]对X1进行修正，步骤如下。

(1) 首先在横截面积没有达到下限的杆件中，根据规则找到第j号杆件的横截面积aj，使其下降到相邻的整数，即第j号杆件的横截面积aj更新为aj-1。

(2) 检查约束条件是否满足，如果满足，跳回步骤(1)继续执行；否则把aj赋回原值，即把aj+1赋值给aj，得到一阶离散局部最优解，记为X2。

(3) 对X2继续修正，减少一个目标函数灵敏度大的杆件面积，同时增加一个目标函数灵敏度小的杆件面积，如果满足约束，那么得到更好的局部最优解X3；否则采用步骤(2)得到的局部离散最优解X2。

由于步骤(2)所得的最优解X2已经达到了一阶局部最优性，步骤(3)将得到满足更高阶精度的局部最优解，如图2的点E。一般来说一阶离散局部最优解能够满足实际需要，为了节省计算量，在本文算例中只追求一阶离散局部最优解X2。

现对上述改进方法的步骤(1)需要满足的规则进行详细阐述，本文有两种下降规则，第一种是需要提供当前点的解析灵敏度，称为相对灵敏度商规则；第二种是需要计算相邻两步之间的差分值，称为相对差商规则。采用两种规则所得到的最优解一般是不同的(但通常很接近)，本文可以选取其中较好的一组作为离散最优解。

首先介绍相对灵敏度商规则。假设第i号杆件的面积ai发生改变，目标函数的灵敏度可以写为

∂W/∂ai=ρili

(15)

约束函数的灵敏度可以写为

(16)

(1) 在全部nm根杆件中，如果存在第j号杆件，使得约束函数的灵敏度∂g/∂aj≥0，那么选取第j号杆件的面积aj变为aj-1。事实上X1的分量中，满足这样条件的aj很可能已经达到下限。若不存在则转向下一步。

(2) 全部nm根杆件中，∂g/∂ai<0 (i=1,…,nm)，本文知道选取使目标函数下降较快，而约束函数上升较慢的杆件来调整比较有利，所以定义参数

(17)

找出其中的最大值βj≥βi(i=1,…,nm)，对应的杆件j，面积aj变为aj-1。

相对差商规则和相对灵敏度商规则比较类似，假设第i号杆件的面积ai发生改变，目标函数的差分方程可以写为

(18)

约束函数的差分方程可以写为

(19)

(1) 在全部nm根杆件中，如果存在第j号杆件，使得约束函数的差分敏度Δg/Δaj≥0，那么选取第j号杆件的面积aj变为aj-1。事实上X1的分量中，满足这样条件的aj很可能已经达到下限。若不存在则转向下一步。

(2) 全部nm根杆件中，Δg/Δai<0(i=1,…,nm)，由于选取使目标函数下降较快而约束函数上升较慢的杆件来调整比较有利，所以定义参数

(20)

找出其中最大值βj≥βi(i=1,…,nm)，对应的杆件j，面积aj变为aj-1。

值得注意的是相对灵敏度商规则的使用有一个前提，即当前点和将要移动到的点两者的约束灵敏度符号必须一致，郭旭等[30]已经证明了在桁架结构中存在这种单调性特征，所以使用相对灵敏度商规则也是有理论依据的。

2.4 鲁棒圆整法求解离散优化问题的流程

本文给出了离散优化问题的鲁棒圆整法流程，如图4所示。

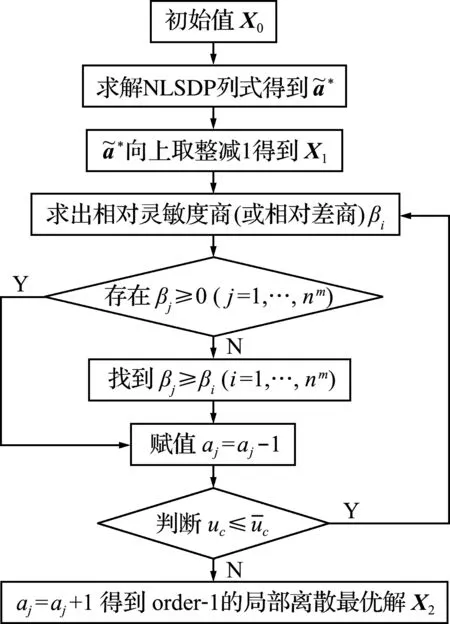
图4 鲁棒圆整法流程

2.5 鲁棒圆整法求解离散优化问题的数值算例

本节通过2个桁架结构重量极小化问题说明鲁棒圆整法的有效性。所有杆件的弹性模量是 100 GPa，密度为10 g/cm3，横截面积初始值为1 cm2。

算例129杆桁架结构

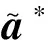
图5 29杆桁架

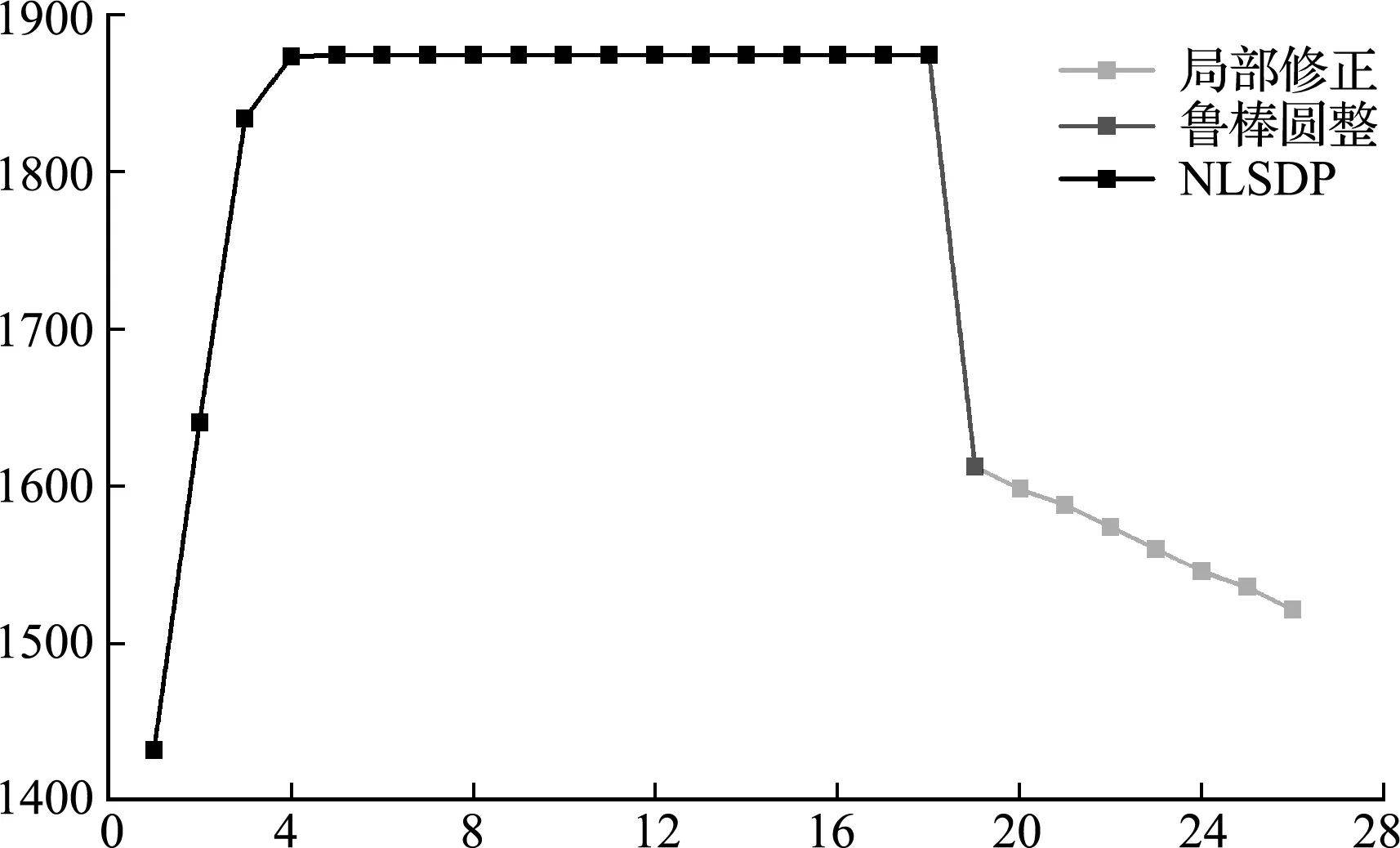
图6 29杆离散结构优化问题目标函数的鲁棒圆整法迭代曲线

算例251杆桁架结构

如图7所示的51杆桁架结构，所有杆件的横截面积只能在[3,100]取整数值。外载荷向量f=(10,0)TkN作用在3,5,7,9,11号节点上。约束为13号杆件的水平方向位移u13x不大于1 cm。表2列出了鲁棒圆整法和传统连续优化圆整法所得的最优横截面积及结构重量等的比较。由表2可知，鲁棒圆整得到的离散解X1满足约束条件，一阶离散局部最优解X2非常接近于连续优化的最优解，而传统连续优化圆整(四舍五入)后并不满足约束条件。

图7 51杆桁架结构

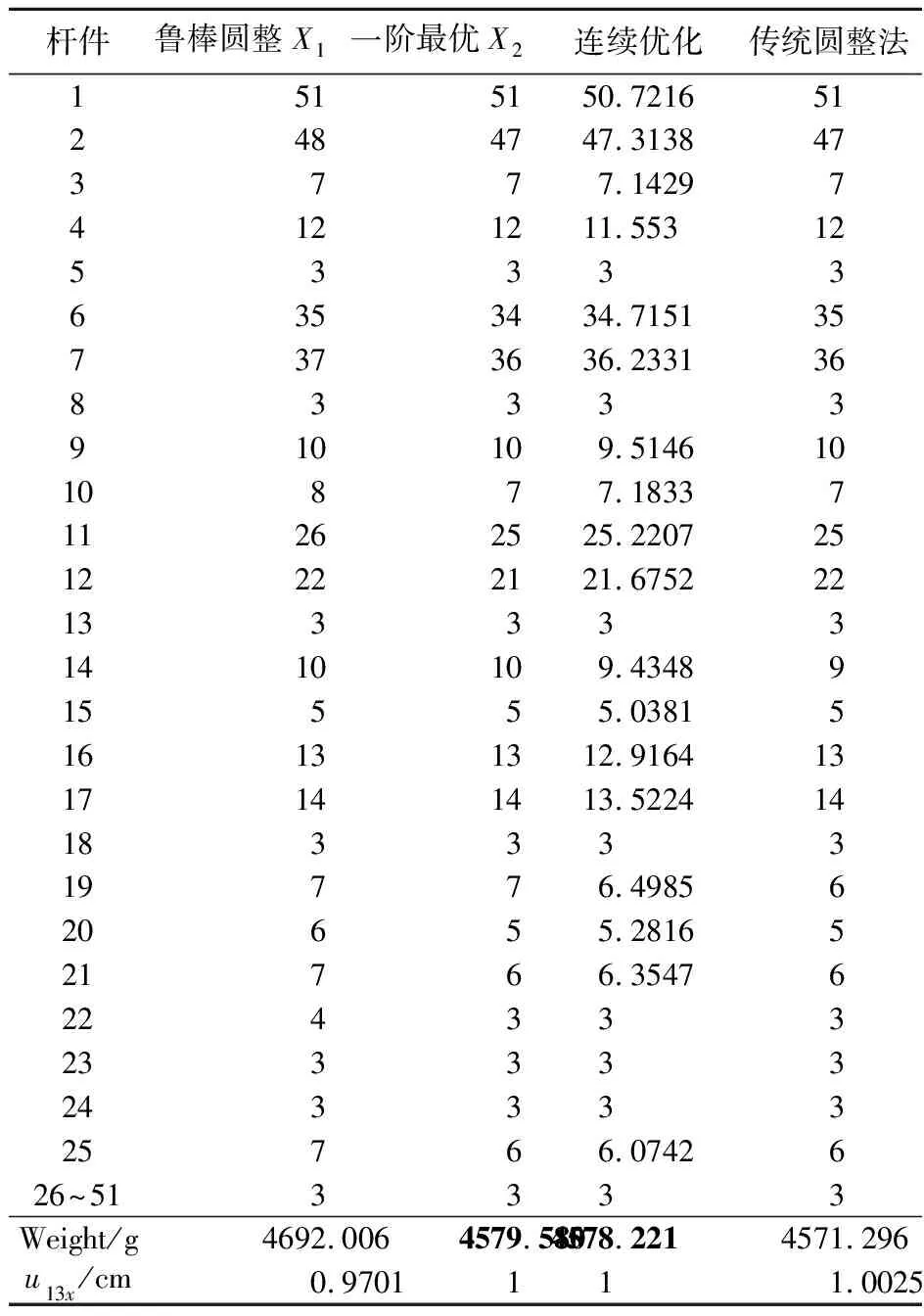
表2 鲁棒圆整法和传统连续优化圆整法最优解的比较(单位：cm2)

3 鲁棒圆整法求解刚度不确定的

离散鲁棒优化问题

刚度不确定的鲁棒优化问题可以使用单层的NLSDP方法[25]求解，但所得到的最优杆件横截面积仍然在正数范围内取连续值，而实际杆件横截面积的取值通常是一个离散数的集合。这就需要把考虑参数的不确定性和设计变量的离散性相结合，发展求解鲁棒问题可置信性离散最优解的方法。本文分两个小节分别介绍使用鲁棒圆整法求解离散鲁棒优化问题的数学模型和离散可行解的修正方法，最后通过数值算例证明方法的可靠性。

3.1 离散鲁棒优化问题的模型和求解

以刚度不确定的桁架结构重量极小化问题为例，假设横截面积为正整数，本文首先给出离散鲁棒优化的数学规划列式，

(21)

本文考虑两种刚度不确定性刻画方法,

(22)

鲁棒圆整法需要求解的鲁棒优化问题就是采用这种不确定性模型。

(23)

(24)

(25)

3.2 离散鲁棒优化问题离散鲁棒可行解的修正

如2.3节所述，本文可以利用相对灵敏度商的规则对离散鲁棒可行解X1进行修正，步骤如下。

(1) 首先在横截面积未达到下限的杆件中，根据规则将第j号杆件的横截面积aj更新为aj-1。

(2) 检查约束条件是否满足。如果满足，跳回步骤(1)继续执行；否则把aj赋回原值，即把aj+1赋值给aj，得到满足鲁棒性约束条件的一阶离散局部最优解X2。

与离散优化问题的区别是，离散鲁棒优化问题每次判断最优解是否满足约束时，都要进行鲁棒问题的结构极值响应分析，本文可以采用郭旭等[30]提出的精确结构极值响应方法，或者基于灵敏度定界的结构极值响应方法[31]求得位移极值，这样就可以检查每一步设计变量改变后能否满足约束条件。

但不确定问题的精确位移极值响应的求解过程比确定性问题位移的求解要复杂很多，计算量很大。若在中间过程使用快速的近似算法替代，直到继续改进离散解会违反约束时，再采用精确的结构位移极值响应分析方法进行严格检验，则可避免在迭代中频繁使用全局最优化算法，从而提高整体计算效率。

(26)

除了较为精确，单调性方法的另一个好处是在每一步迭代中几乎不增加任何计算量，因为在采用相对灵敏度商规则判断下降方向的时候，已经进行过灵敏度分析。

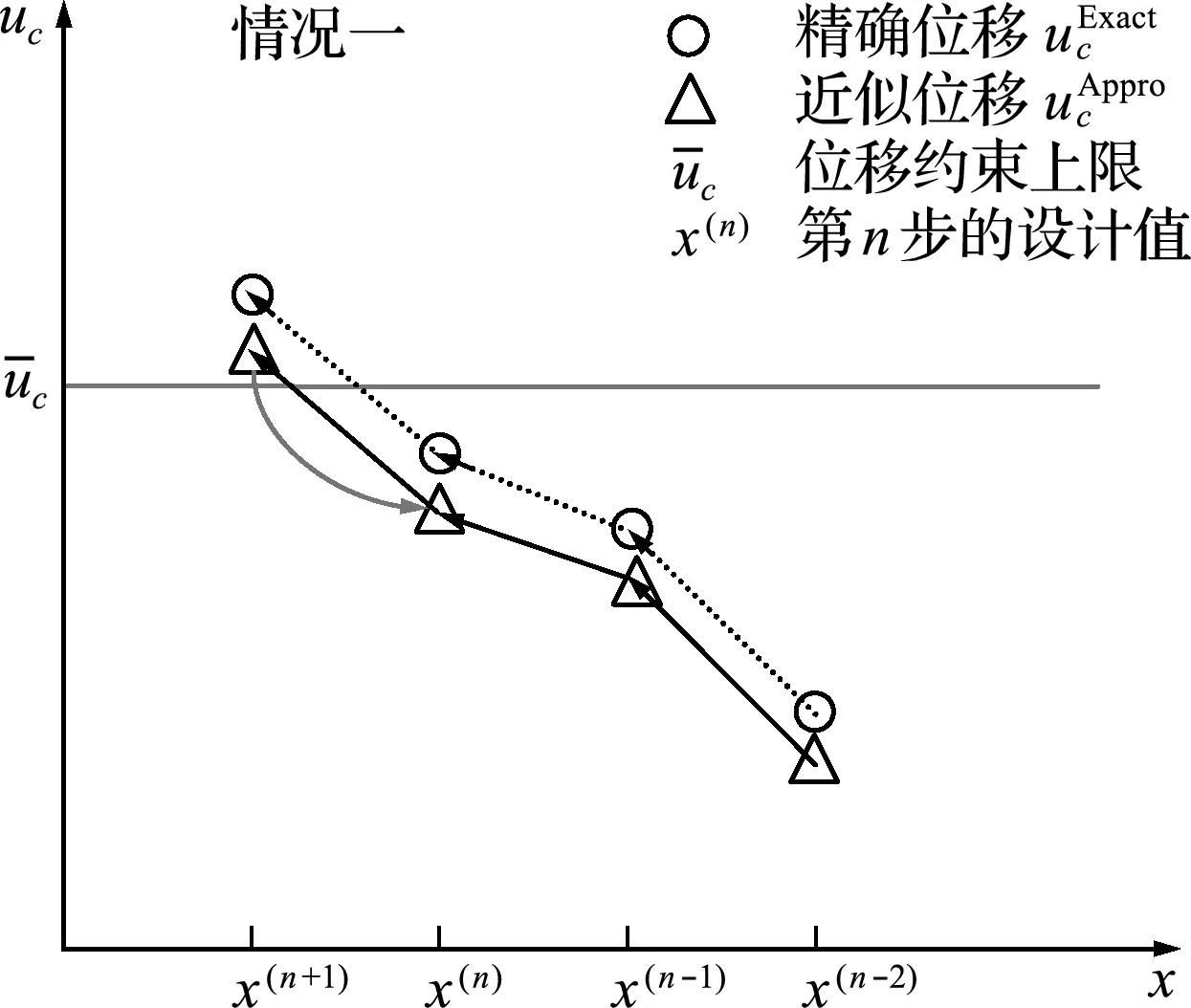
图8 离散鲁棒优化问题收敛过程(一)

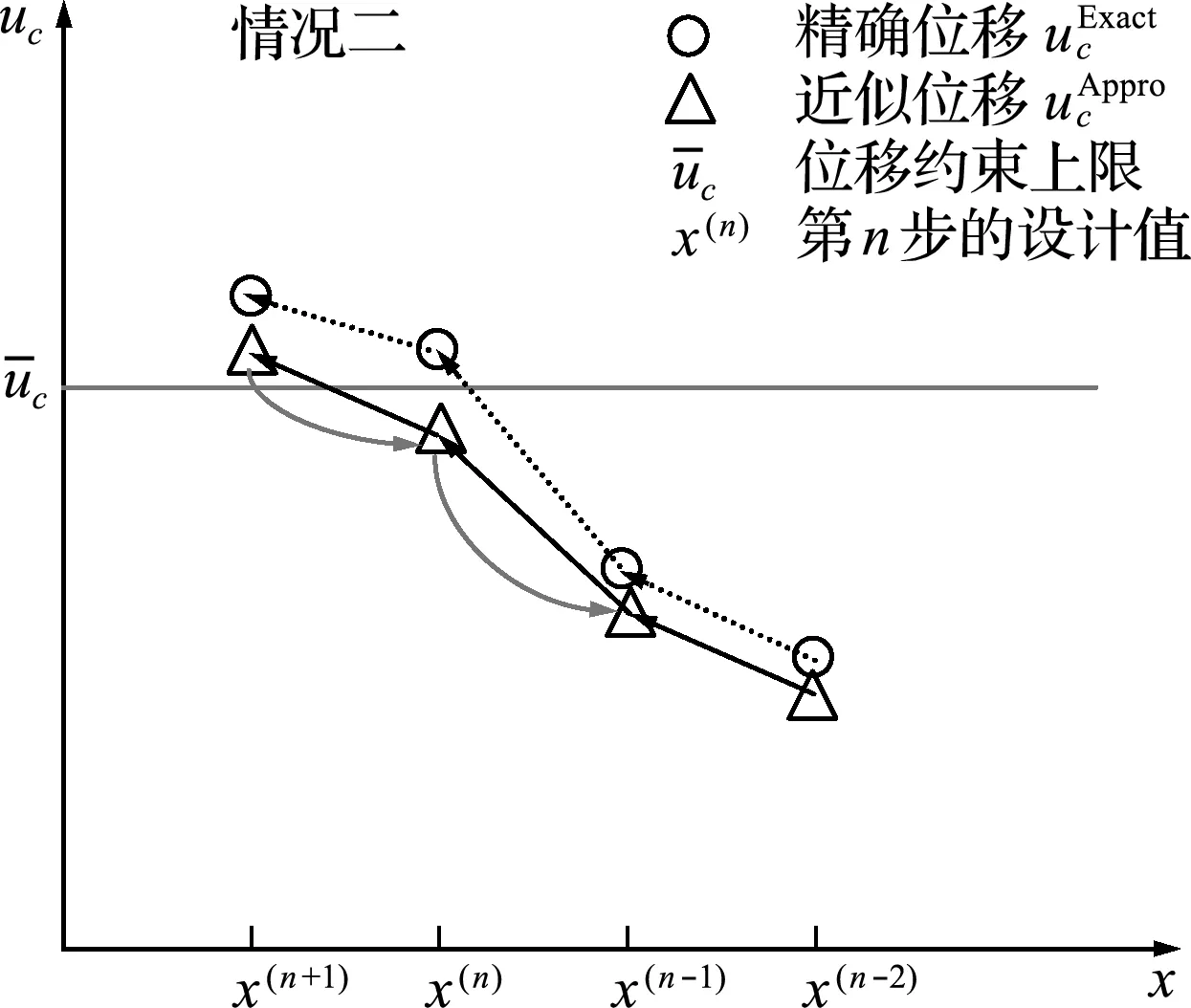
图9 离散鲁棒优化问题收敛过程(二)

3.3 离散鲁棒优化问题的数值算例

算例329杆桁架结构

图10 29杆离散鲁棒优化问题目标函数的迭代曲线

表3 离散鲁棒优化和连续鲁棒优化最优解的比较(单位：cm2)

算例451杆桁架结构

如图7所示的51杆桁架，规定所有杆件的横截面积为[3,100]的整数值。外载荷和约束条件等与算例2相同。表4列出了离散鲁棒优化和连续鲁棒优化所得的最优横截面积及结构重量等的比较。由表4可知，离散鲁棒优化得到的最优解能够满足鲁棒性约束条件，且与连续鲁棒优化最优解的目标函数非常接近，保证了其最优性。

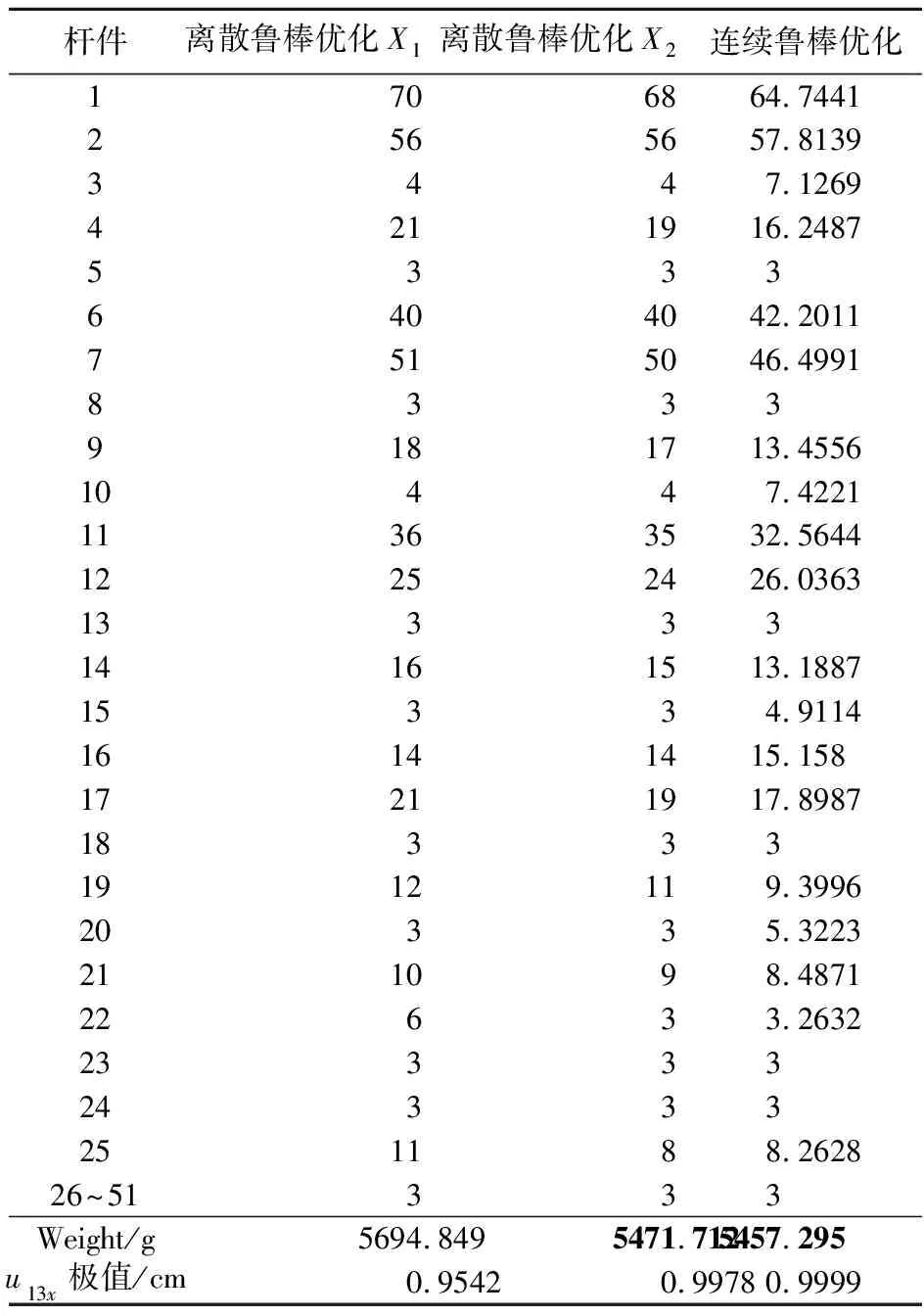
表4 离散鲁棒优化和连续鲁棒优化最优解的比较(单位：cm2)

4 结 论

本文提出了与离散优化列式等价的鲁棒优化列式，并证明了两者的等价性。把可置信性鲁棒结构优化思想应用到离散优化中，提出了用于解决离散优化问题的鲁棒圆整法，并进一步拓展到考虑刚度不确定性的离散鲁棒优化中。鲁棒圆整法首先通过可置信性单层NLSDP算法求解所构造的鲁棒优化问题得到连续最优解，然后在鲁棒性区域内进行圆整得到可理论上保证满足约束条件的离散解，最后利用相对差商规则或者相对灵敏度商规则进行修正，得到一阶离散局部最优解。相对于传统的连续优化圆整法来说，本文提出的鲁棒圆整法的优势是能够严格保证离散解的可行性。此外，本文提出的结构可置信性离散鲁棒优化方法在计算耗费上和连续鲁棒优化相似，因而具有较大的应用价值。

参考文献(References):

[1] 加里，约翰逊.计算机和难解性[M].张立昂，沈 泓,译.北京:科学出版社,1987.(Garey M R,Johnson D S.ComputersandIntractability[M].ZHANG Li-ang,SHEN Hong,translated.Beijing:Science Press,1987.(in Chinese))

[2] Papadimitriou C H,Steiglitz K.组合最优化算法和复杂性[M].北京:清华大学出版社,1988.(Papadi-mitriou C H,Steiglitz K.CombinatorialOptimization:AlgorithmsandComplexity[M].Beijing:Tsinghua University Press,1988.(in Chinese))

[3] 隋允康,袁晓兵,叶宝瑞,等.力学映射下板壳结构的截面离散优化设计[J].工程力学,2006,23(8):1-5,11.(SUI Yun-kang,YUAN Xiao -bing.YE Bao -rui,et al.Discrete optimized design of shell structures based on mechanics mapping[J].EngineeringMechanics,2006,23(8):1-5,11.(in Chinese))

[4] Arora J S,Huang M W,Hsieh C C.Methods for optimization of nonlinear problems with discrete variables:A review[J].StructuralOptimization,1994,8(2-3):69-85.

[5] 陈立周.工程离散变量优化设计方法原理与应用[M].北京:机械工业出版社,1989.(CHEN Li-zhou.EngineeringDiscreteVariableOptimizationDesignMethodPrincipleandApplication[M].Beijing:China Machine Press,1989.(in Chinese))

[6] Chai S,Sun H C.A relative difference quotient algorithm for discrete optimization[J].StructuralOptimization,1996,12(1):46-56.

[7] Templeman A B,Yates D F.A linear programming approach to the discrete optimum design of trusses[J].EngineeringOptimization,1982.

[8] 李兴斯,谭 涛.离散变量结构优化设计的连续化方法[J].应用力学学报,2007,24(1):26-30，171.(LI Xing-si,TAN Tao.Continuous approach to discrete structural optimization design with discrete variables[J].ChineseJournalofAppliedMechanics,2007,24(1):26-30，171.(in Chinese))

[9] 谭 涛.离散变量优化设计的连续化方法研究[D].大连:大连理工大学,2006.(TAN Tao.Research on Continuous Method of Discrete Variable Optimization Design[D].Dalian University of Technology,2006.(in Chinese))

[10] 石连拴,柴 山,孙焕纯.离散变量结构优化设计序列定界组合算法研究[J].大连理工大学学报,1999,39:591-596.(SHI Lian-shuan,CHAI Shan,SUN Huan-chun.Application of a sequential delimitative and combinatorial algorithm to discrete optimum design of structures[J].JournalofDalianUniversityofTechnology,1999,39(5):591-596.(in Chinese))

[11] 王跃方,孙焕纯.离散变量桁架结构的布局优化设计[J].大连理工大学学报,1995,35(4):458-462.(WANG Yue -fang,SUN Huan-chun.On layout optimization of truss structures with discrete sizing variables[J].JournalofDalianUniversityofTechnology,1995,35(4):458-462.(in Chinese))

[12] Juang D S,Chang W T.A revised discrete Lagran-gian-based search algorithm for the optimal design of skeletal structures using available sections[J].StructuralandMultidisciplinaryOptimization,2006,31(3):201-210.

[13] Wolkowicz H,Anjos M F.Semidefinite programming for discrete optimization and matrix completion problems[J].DiscreteAppliedMathematics,2002,123(1-3):513-577.

[14] Bertsimas D,Sim M.Robust discrete optimization and network flows[J].MathematicalProgramming,2003,98(1-3):49-71.

[15] Royset J O,Der Kiureghian A,Polak E.Reliability-based optimal design of series structural systems[J].JournalofEngineeringMechanics,2001,127(6):607-614.

[16] Ben-Tal A,Nemirovski A.Robust solutions of Linear Programming problems contaminated with uncertain data[J].MathematicalProgramming,2000,88(3):411-424.

[17] Ben-Tal A,Nemirovski A.Robust convex optimization[J].MathematicsofOperationsResearch,1998,23(4):769-805.

[18] Ben-Tal A,Nemirovski A.Robust solutions of uncertain linear programs[J].OperationsResearchLetters,1999,25(1):1-13.

[19] El Ghaoui L,Lebret H.Robust solutions to least-squares problems with uncertain data[J].SIAMJournalonMatrixAnalysisandApplications,1997,18(4):1035-1064.

[20] El Ghaoui L,Oustry F,Lebret H.Robust solutions to uncertain semidefinite programs[J].SIAMJournalonOptimization,1998,9(1):33-52.

[21] Boyd S,Vandenberghe L.ConvexOptimization[M].Cambridge:Cambridge University Press,2004.

[22] Ben-Tal A,Nemirovski A.Robust optimization -methodology and applications[J].MathematicalPro-gramming,2002,92(3):453-480.

[23] Calafiore G,El Ghaoui L.Ellipsoidal bounds for uncertain linear equations and dynamical systems[J].Automatica,2004,40(5):773-787.

[24] Chen S H,Wu J,Yu Y D,et al.Interval optimization for uncertain structures[J].FiniteElementsinAn-alysisandDesign,2004,40:1379-1398.

[25] Guo X,Du J M,Gao X X.Confidence structural robust optimization by non-linear semidefinite pro -gramming-based single -level formulation[J].InternationalJournalforNumericalMethodsinEnginee-ring,2011,86(8):953-974.

[26] Kang Z,Bai S.On robust design optimization of truss structures with bounded uncertainties[J].StructuralandMultidisciplinaryOptimization,2013,47(5):699-714.

[27] Bai S,Kang Z.Robust topology optimization for structures under bounded random loads and material uncertainties[J].Computers&Structures,2021,252:106569.

[28] Guo X,Bai W,Zhang W S,et al.Confidence structural robust design and optimization under stiffness and load uncertainties[J].ComputerMethodsinAppliedMechanicsandEngineering,2009,198(41-44):3378-3399.

[29] Liu J T,Gea H C.Robust topology optimization under multiple independent unknown-but-bounded loads[J].ComputerMethodsinAppliedMechanicsandEngineering,2018,329:464-479.

[30] Guo X,Bai W,Zhang W S.Extreme structural response analysis of truss structures under material uncertainty via linear mixed 0-1 programming[J].InternationalJournalforNumericalMethodsinEngineering,2008,76(3):253-277.

[31] Du J M,Du Z L,Wei Y H,et al.Exact response bound analysis of truss structures via linear mixed 0-1 programming and sensitivity bounding technique[J].InternationalJournalforNumericalMethodsinEngineering,2018,116(1):21-42.

[32] McWilliam S.Anti-optimisation of uncertain structures using interval analysis[J].Computers&Structures,2001,79(4):421-430.