基于主动学习Kriging模型与序列重要抽样的随机-区间混合可靠性分析

(大连理工大学 工程力学系 工业装备结构分析国家重点实验室,大连 116024)

1 引 言

不确定性广泛存在于物理系统的整个生命周期中，随着实际问题日益复杂，描述材料属性、结构几何、载荷条件以及制造公差等的不确定性信息呈现多元化特点，通常可分为随机不确定性和认知不确定性。前者描述的是物理系统的固有特性，通常采用概率形式量化；后者则是由于对物理系统的认识水平和信息缺乏而产生的认知差异，通常采用区间形式量化。实际工程的不确定分析问题中，随机与认知不确定性经常同时存在，因此解决多种类型不确定性变量的混合可靠性分析越来越受关注。

近年来，众多国内外学者对混合可靠性问题进行了深入的研究。王睿星等[1]综述了已有的4种主要非概率可靠性模型，针对线性功能函数分别从度量原理、可靠性指标物理意义、适用范围和结果精度等方面对各模型进行了对比和总结。郭书祥等[2]结合结构的概率和非概率混合模型，通过两级功能方程的逐次建立及可靠性分析,给出结构可靠的概率度量。Du[3]提出了基于一阶可靠性方法的FORM(First Order Reliability Method)的统一不确定性分析方法，称为FORM-UUA，可以处理具有高鲁棒性的黑箱功能函数；Guo等[4]基于该方法对具有随机变量和区间变量的混合可靠性问题进行了敏感性分析。Jiang等[5]构造了一个等效的随机变量单层优化算法，改进了双层循环算法的效率和稳定性，可计算最大失效概率。贾大卫等[6]采用Laplace渐进积分法分析了凸集-概率混合模型的结构可靠性问题。上述方法在处理功能函数高非线性和多设计点的情况容易出现计算失真。

在可靠性分析方法中，蒙特卡洛模拟MCS(Monte Carlo Simulation)是适用性和鲁棒性最好的方法，不受随机变量数目和功能函数形式的影响。但是在求解小失效概率问题时，需要大量的随机样本。为了解决MCS方法计算效率低的问题，往往采用减少方差的模拟方法，其中重要性抽样通过引入重要性抽样函数，来提高随机样本落入失效区域的几率。Liu等[7]提出了一种基于FORM-UUA的重要抽样法用于处理随机和相关区间变量的混合可靠性问题，但是当功能函数具有高非线性或者多设计点的情况下，该方法很难准确定位失效面附近，进而影响最终失效概率的准确性。序列重要抽样方法SIS(Sequential Importance Sampling)是一种有效的自适应重要抽样方法，通过中间分布的逐级采样逼近最优重要抽样函数，渐近收敛的特性使得算法处理复杂功能函数更加有效，在随机不确定性分析领域得到广泛应用，包括可靠性分析[8,9]、可靠性灵敏性分析[10]及可靠性优化[11]等。

同时，为了节省耗时功能函数的可靠性分析的计算成本，代理模型技术在可靠性分析领域得到广泛应用。Kriging[12,13]模型是最常用的代理模型之一，本质上是一个高斯过程模型，可以给出功能函数在未知点的预测均值和预测方差，为后续改进代理模型的精度提供了更多的可能。Yang等[14]将主动学习Kriging与MCS方法相结合用于解决随机-区间混合可靠性问题，称为ALK-HRA方法(Active Learning Kriging model for Hybrid Reliability Analysis)。Zhang等[15]提出一种基于投影边界的主动学习方法，提高了ALK-HRA方法的效率。但是基于MCS的方法在面对小失效概率问题时，过大的样本数使得主动学习过程变得繁杂耗时。

本文将序列重要抽样方法与主动学习Kriging模型结合，提出了一种有效处理随机-区间混合可靠性问题的方法。在序列重要采样方法中采用高斯混合分布作为提议分布进行逐级采样，通过合理选择高斯混合分布的参数使得算法适用于复杂功能函数；提出了构建Kriging模型的两步主动学习策略，在保证算法准确性的前提下显著提高计算效率。

2 随机-区间混合可靠性问题

对于随机变量和区间变量同时存在的混合可靠性问题，功能函数G(X,Y)包含随机变量X和区间变量Y。考虑区间变量，可以定义功能函数的上下界为

Gmax(X)={maxYG(X,Y)|Y∈D}

(1)

Gmin(X)={minYG(X,Y)|Y∈D}

(2)

式中D=[YL,YU]为区间变量取值范围，Gmin(X)和Gmax(X)分别为区间变量影响下功能函数的最小值和最大值，图1给出了设计空间中的失效区域。定义失效概率的上下边界为

图1 混合可靠性问题失效区域

(3)

(4)

混合可靠性分析就是计算失效概率的上下边界，这是一个双循环的过程，内层循环采用优化算法求解功能函数的极值响应，外层循环采用概率分析方法求解失效概率。可以采用蒙特卡洛方法MCS求解式(3,4)。首先，根据随机变量分布函数产生大量样本，然后估计每一个样本在区间变量影响下的最大和最小响应，最终统计失效响应的占比即可得到失效概率。虽然MCS方法具有很强的鲁棒性和适应性，但是计算成本较大。

3 基于主动学习Kriging的序列重要抽样方法

3.1 混合可靠性分析的序列重要抽样方法

重要性抽样通过引入合理的重要抽样函数h(X)，使得产生样本落入失效区域的概率增加，从而提高采样效率。在重要性抽样中，失效概率的计算式表示为

(5)

(6)

(7)

(8)

重要抽样方法的关键是合理选取重要抽样函数hU(X)和hL(X)。如果选取得当，可以显著降低采样方差，节省计算成本。理论上存在最优的重要抽样函数使采样方差为0，形式如下

(9)

(10)

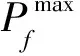
(11)

式中Φ(·)为标准正态累积分布函数。随着参数σ逐渐趋近于0，光滑函数对于指示函数的近似效果越好，即存在如下极限情况

(12)

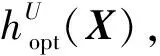
(13)

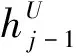
(14)

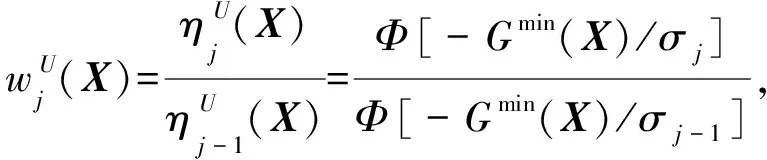
(15)

中间分布的参数选择是SIS方法的重要组成部分。为了确保相邻中间分布之间的归一化常数比估计值式(15)的准确性，应该合理选择参数σ使得相邻分布之间的差异不大。文献[9]提出了一种自适应的参数σ选取方式。即在SIS的每一个迭代步中，可以通过求解下面的优化问题自适应的选择参数σ。

(16)

(17)

(18)

3.2 主动学习Kriging模型

本文采用Kriging模型近似真实功能函数。实验设计DoE(Design of Experiments)方法影响着Kriging模型的精度与效率，虽然可以通过DoE方法选取足够多的样本来提高Kriging模型的精度，但是会增加计算负担。为了平衡样本数和模型精度，学者们提出了构建代理模型的主动学习方法，通过少量的初始样本构建Kriging模型，然后采用某种学习方案序列的增加样本点，逐步提高Kriging模型的精度，如U准则[18]、EFF准则[19]和H准则[20]等。其中U准则是一种简单高效的主动学习策略，旨在将Kriging预测最不准确的点逐次加入到训练样本中。其学习函数如下

(19)

3.3 本文方法流程

本文提出基于主动学习Kriging模型与序列重要抽样方法相结合的ALK-HRA-SIS方法，求解随机-区间混合可靠性问题。SIS方法通过分布序列的逐级采样，将初始样本逐渐转移到近似最优的重要密度函数附近。当与主动学习Kriging方法相结合时，Kriging模型的近似精度需要满足以下两点需求，一是保证分布序列可以无偏收敛到近似最优的重要密度函数附近，二是确保最终的重要采样过程计算失效概率的准确性。因此，本文提出了两步主动学习策略，即在SIS方法的分布序列第一级和最后一级分别进行Kriging主动学习。第一个主动学习过程针对SIS分布序列的初始样本集，第一次提高Kriging模型的预测精度，以获得功能函数的整体近似。第二个主动学习过程针对SIS分布序列的最终重要样本集，第二次提升Kriging模型预测精度，保证最终失效概率计算的准确性。图2为基于主动学习Kriging模型的序列重要抽样方法流程，具体步骤如下。

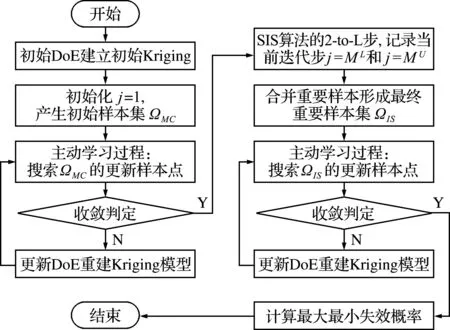
图2 本文方法ALK-HRA-SIS流程

(1) 初始化Kriging代理模型。采用拉丁超立方抽样在变量空间产生少量初始DoE样本，随机变量采用均值附近5倍标准差作为采样范围，区间变量采样范围即为变量界限。利用Matlab toolbox DACE建立初始化的代理模型。

(2) 产生初始样本集。迭代步j=1，为了计算失效概率的上下边界，SIS方法需要两个分布序列，其初始分布相同(随机变量的初始概率分布)，可以采用相同的初始样本集ΩM C。对于随机变量，根据分布产生随机样本；对于区间变量，采用LHS产生样本。

(3) 主动学习过程。使用Kriging模型预测初始样本集ΩM C的预测值和预测方差，采用U准则识别需要更新的样本点，加入到训练样本中，重新建立Kriging代理模型，重复上述过程，样本集上的U值最小值满足min(U)≥2时停止更新。

(4) 构造SIS分布序列。对于失效概率的上下边界，需要分别构造SIS的分布序列。采用上面步骤给出的Kriging模型，依照式(13～16)分别构造用于计算失效概率上下边界的分布序列，当两个分布序列收敛时，记录当前算法迭代步为j=ML和j=MU。

(20)

(21)

(6) 主动学习过程。使用Kriging模型预测样本集ΩI S的预测值和预测方差，采用U准则识别需要更新的样本点，加入到训练样本中，重新建立Kriging代理模型，重复上述过程，样本集上的U值最小值满足min(U)≥2时停止更新。

(7) 失效概率计算。根据式(17，18)，采用Kriging模型预测失效概率的上下边界。

4 算例分析

通过三个算例将本文提出的ALK-HRA-SIS算法与其他几种常用的混合可靠性分析方法进行比较，包括MCS、SIS、FORM-UUA[3]和ALK-HRA[14]，说明本文方法的计算效率和精度。对于每个算例，MCS采用200×106次真实功能函数调用，其中根据随机变量概率分布产生106个样本，根据区间变量产生200个样本，参考解是独立运行MCS方法10次所得的平均值。

4.1 算例1

本算例来源于文献[19]，本文对其进行了适当修改，功能函数如下,

(22)

式中x1和x2是相互独立的正态分布随机变量，x1～N(1.5,1)，x2～N(2.5,1)，y为区间变量，取值范围是[2,2.5]。已有研究[19]表明，该算例的功能函数在标准正态空间形状复杂，呈高非线性和多峰特性。本算例中，ALK-HRA-SIS方法初始样本集ΩM C个数为5000，每个中间分布取样个数为2000。

表1给出了不同方法的计算结果，其中，Pmax和Pmin分别为失效概率的上下界限，Ncall为调用实际功能函数的次数，相对误差(%)(U/L)为失效概率结果与MSC方法参考解的相对误差，U和L分别对应失效概率的上下界。

表1 算例1结果

由表1可知，FORM-UUA是基于一阶可靠度法的统一不确定性分析方法，分别采用了441次和1114次功能函数调用近似求解失效概率的上下界限，Ncall为二者的和1555次，失效概率结果相对误差很大，Pmax的相对误差达到了274.25%。ALK-HRA的功能函数调用次数为初始DoE样本和主动学习增加样本数目相加，共51次。本文提出的ALK-HRA-SIS实际功能函数为初始DoE样本与两次主动学习过程增加样本数目相加，共41次。SIS,ALK-HRA和ALK-HRA-SIS方法的失效概率相对误差均较小，其中SIS方法结果最接近MCS参考解，但计算量很大。相比ALK-HRA，本文的ALK-HRA-SIS方法计算精度更高，误差小于1%，而且功能函数调用次数更少，降低了样本池的规模，提升了算法的计算效率。

图3给出了本文方法获得的最终重要抽样样本与真实失效面，可以看出，ALK-HRA-SIS方法可以准确定位失效面的两个重要区域。同时，获得的两组重要样本的分布变化也捕捉到了最大与最小失效面的重要区域的变化。

图3 ALK-SIS最后一级样本

4.2 算例2

该算例是概率可靠性领域常用的例子，本文稍作修改，功能函数如下,

(23)

式中x1和x2为相互独立的标准正态随机变量，y是区间变量，取值范围为[2.5,3.2]。标准正态空间中，该算例的失效域具有多个设计点，同时失效域是断开的。FORM-UUA无法求解多设计点问题。

在本算例中，ALK-HRA和ALK-HRA-SIS方法的初始DoE设置为12。表2给出了不同方法的结果对比。尽管SIS精度很好，但函数调用次数太多；相比ALK-HRA方法，本文的方法在计算效率(功能函数调用次数43=12+20+11)和计算精度(误差分别为1.32%和1.60%)方面都有优势，说明本文方法可有效解决功能函数多设计点和高非线性问题。

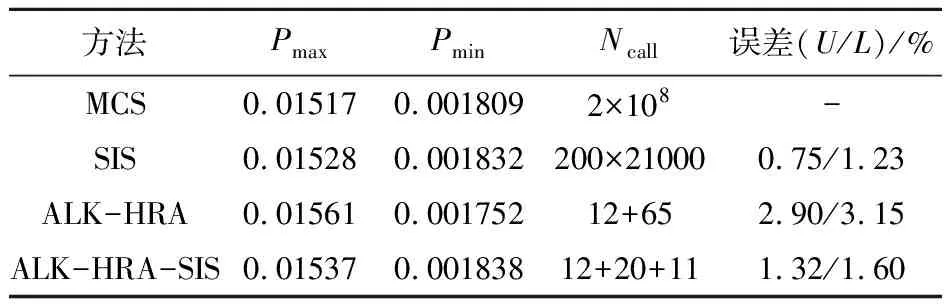
表2 算例2结果

图4给出了标准正态空间中本文方法样本点逐渐向最优重要抽样函数收敛的过程，算法在4步迭代之后收敛到重要失效区域，准确捕捉到了最优和次优失效面，同时重要样本的分布比例也表明了两个失效区域对于失效概率的贡献程度。

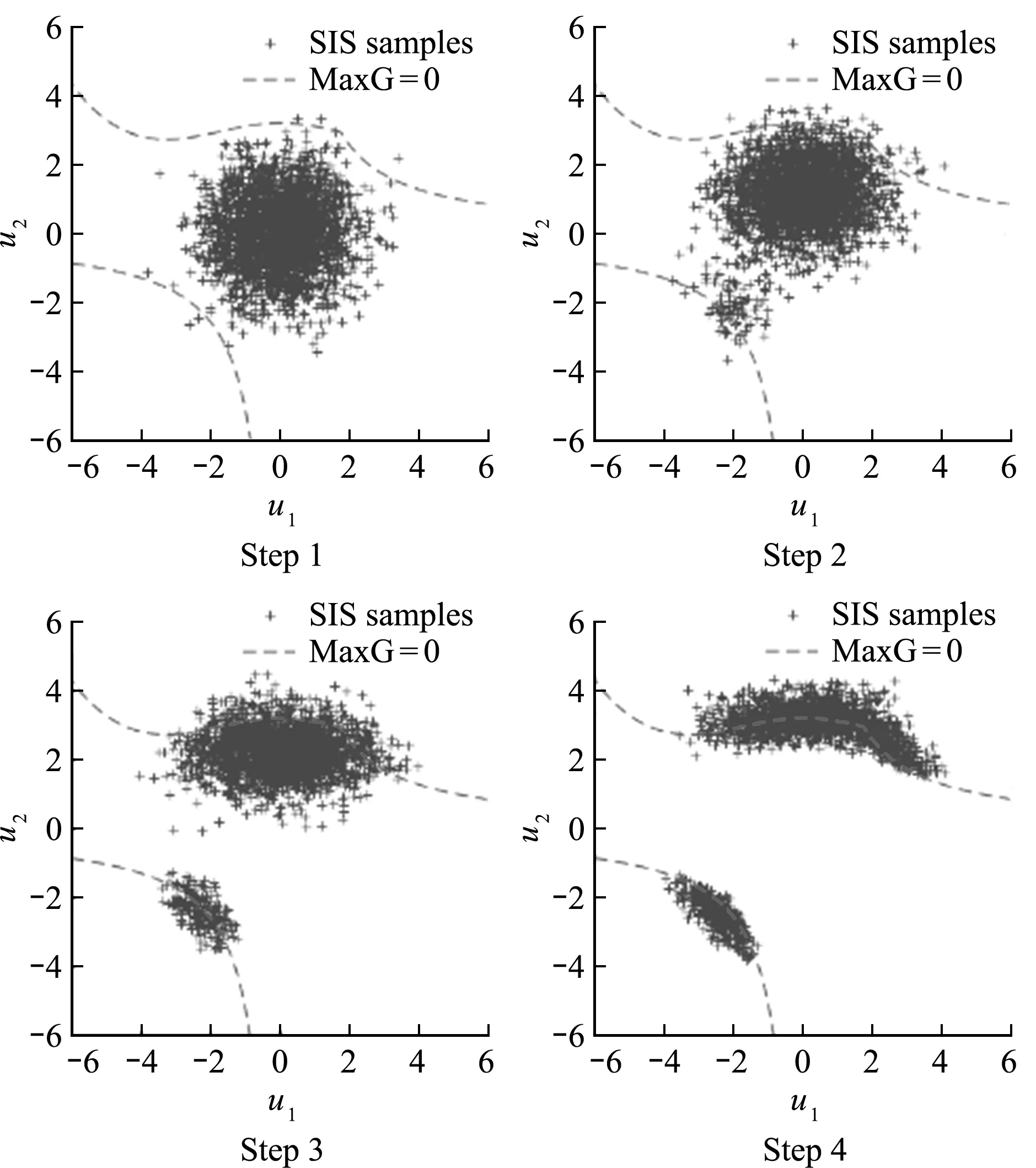
图4 对应失效概率下界的SIS样本收敛过程

4.3 算例3

如图5所示，屋顶结构受到均匀分布荷载q作用。顶层与压杆材料为混凝土，而底层与拉杆由钢材料构成。在结构分析中，均匀分布载荷等效为三个节点载荷，大小为P=ql/4。表3给出了随机和区间变量的参数信息。功能函数定义如下，

表3 屋顶结构不确定性变量

图5 屋顶结构

(24)

式中EC和ES分别为混凝土和钢筋的杨氏模量，AC和AS分别为其横截面积。功能函数表示节点C竖向挠度大于0.025 m则结构失效。

该算例有2个区间变量，因此采用400个区间样本用于估计失效概率的极值。同样，ALK-HRA与ALK-HRA-SIS方法的初始DoE设置为12。可以看出，对于屋顶结构混合可靠性问题，FORM-UUA相对误差最大，ALK-HRA与本文方法的相对误差均很小，本文方法的计算精度更高，真实函数调用次数更少(46次)。

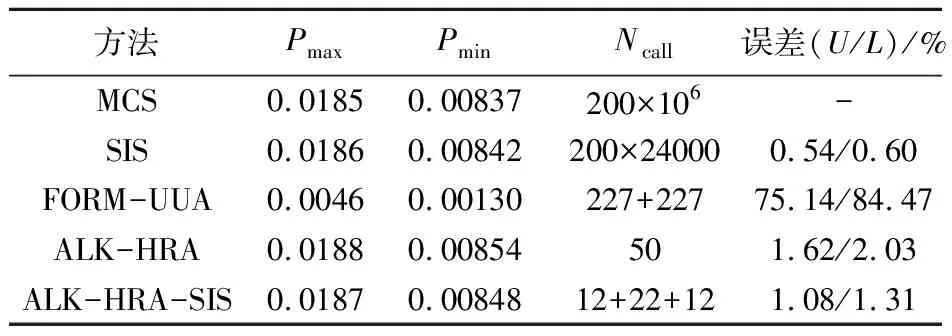
表4 算例3结果

5 结 论

对于随机-区间混合可靠性分析中的复杂功能函数，如高非线性和多设计点，本文提出了结合序列重要抽样方法和主动学习Kriging模型的ALK-HRA-SIS方法。通过自适应的分布序列逐级采样，实现对最优重要抽样密度的近似取样，采样过程中使用主动学习Kriging模型近似计算样本响应值，显著降低了功能函数的调用次数，在保证结果精度的同时提高了序列重要抽样的计算效率。算例分析表明，与FORM-UUA相比，本文方法对于高非线性及多设计点问题的处理能力更强；与ALK-HRA方法相比，降低了样本池的规模，提高了实际问题的计算效率。

参考文献(References):

[1] 王睿星,王晓军,王 磊,等.几种结构非概率可靠性模型的比较研究[J].应用数学和力学,2013,34(8):871-880.(WANG Rui-xing,WANG Xiao -jun,WANG Lei,et al.Comparisons of several non-probabilistic models for structural reliability[J].AppliedMathematicsandMechanics,2013,34(8):871-880.(in Chinese))

[2] 郭书祥,吕震宙.结构可靠性分析的概率和非概率混合模型[J].机械强度,2002(4):524-526.(GUO Shu-xiang,LÜ Zhen-zhou.Hybrid probabilistic and non-probabilistic model of structural reliability[J].JournalofMechanicalStrength,2002(4):524-526.(in Chinese))

[3] Du X.Unified uncertainty analysis by the first order reliability method[J].JournalofMechanicalDe-sign,2008,130(9):091401.

[4] Guo J,Du X.Reliability sensitivity analysis with random and interval variables[J].InternationalJournalforNumericalMethodsinEngineering,2009,78(13):1585-1617.

[5] Jiang C,Lu G Y,Han X,et al.A new reliability an-alysis method for uncertain structures with random and interval variables[J].InternationalJournalofMe-chanicsandMaterialsinDesign,2012,8(2):169-182.

[6] 贾大卫,吴子燕,何 乡.一种基于凸集-概率混合模型的结构可靠性分析法[J].固体力学学报,2020,41(5):470-484.(JIA Da-wei,WU Zi-yan,HE Xiang.A method for structural reliability analysis based on the convex set-probability hybrid model[J].ChineseJournalofSolidMechanics,2020,41(5):470-484.(in Chinese))

[7] Liu X X,Elishakoff I.A combined importance sampling and active learning Kriging reliability method for small failure probability with random and correlated interval variables[J].StructuralSafety,2020,82:101875.

[8] Katafygiotis L S,Zuev K M.Estimation of small failure probabilities in high dimensions by adaptive linked importance sampling[J].COMPDYN,2007.

[9] Papaioannou I,Papadimitriou C,Straub D.Sequential importance sampling for structural reliability analysis[J].StructuralSafety,2016,62:66-75.

[10] Papaioannou I,Breitung K,Straub D.Reliability sensitivity estimation with sequential importance sampling[J].StructuralSafety,2018,75:24-34.

[11] Beaurepaire P,Jensen H A,Schu⊇ller G I,et al.Reliability-based optimization using bridge importance sampling[J].ProbabilisticEngineeringMechanics,2013,34:48-57.

[12] 刘 阔,李晓雷,王 健.一种基于Kriging模型的机械结构可靠性分析方法[J].东北大学学报(自然科学版),2017(38):1002-1006.(LIU Kuo,LI Xiao -lei,WANG Jian.An analysis method of mechanical structural reliability based on the kriging model[J].JournalofNortheasternUniversity(NaturalScience),2017(38):1002-1006.(in Chinese))

[13] 周昳鸣,张君茹,程耿东.基于Kriging代理模型的两类全局优化算法比较[J].计算力学学报,2015,32(4):451-456.(ZHOU Yi-ming,ZHANG Jun-ru,CHENG Geng-dong.Comparison for two global optimization algorithms based on Kriging surrogate model[J].ChineseJournalofComputationalMechanics,2015,32(4):451-456.(in Chinese))

[14] Yang X,Liu Y,Gao Y,et al.An active learning Kriging model for hybrid reliability analysis with both random and interval variables[J].StructuralandMultidisciplinaryOptimization,2015,51(5):1003-1016.

[15] Zhang J,Xiao M,Gao L,et al.A novel projection outline based active learning method and its combination with Kriging metamodel for hybrid reliability analysis with random and interval variables[J].ComputerMethodsinAppliedMechanicsandEngineering,2018,341:32-52.

[16] Dubourg V,Sudret B,Deheeger F.Metamodel-based importance sampling for structural reliability analysis[J].ProbabilisticEngineeringMechanics,2013,33:47-57.

[17] Picheny V.Improving Accuracy and Compensating for Uncertainty in Surrogate Modeling[D].University of Florida,2009.

[18] Echard B,Gayton N,Lemaire M.AK-MCS:An active learning reliability method combining Kriging and Monte Carlo Simulation[J].StructuralSafety,2011,33(2):145-154.

[19] Bichon B J,Eldred M S,Swiler L P,et al.Efficient global reliability analysis for nonlinear implicit performance functions[J].AIAAJournal,2008，46(10):2459-2468.

[20] Lü Z,Lu Z,Wang P.A new learning function for Kriging and its applications to solve reliability pro -blems in engineering[J].Computers&MathematicswithApplications,2015,70(5):1182-97.