结构多源不确定性反问题的流形学习求解方法

韩 旭*1,， 刘 杰， 陈金龙

(1.河北工业大学 机械工程学院，天津 300401；2.湖南大学 机械与运载工程学院，长沙 410082)

1 引 言

工程反问题是从演化结果出发，根据观测数据或期望达到的性能来探求结构的内部规律或其受外部影响[1]。近几十年来，随着传感与测量技术的进步，以及数值模拟与智能计算方法的涌现，工程反问题理论与方法的研究已有长足发展，为准确获取传统试验测试难以确定的结构参量以及实现复杂工程结构的高精度建模与分析提供了有效途径。工程反问题方法研究主要集中于确定性反问题，即计算反求过程中的测量响应、结构模型和反求参量均在确定性框架下进行处理。然而，实际工程结构在几何、材料、工艺、载荷、测量响应和模型偏差等方面不可避免地存在不确定性因素[2-4]。为此，科学合理地度量工程反问题的复杂不确定性，实现多源不确定性下未知结构参量的高效计算反求，对于反问题的理论发展和工程应用都具有重要意义。

根据不确定性的来源不同，工程不确定性反问题可概括分为测量不确定性反问题和模型不确定性反问题。对于测量不确定性反问题，以发展成熟的概率理论为基础，早期主要发展了最大似然估计方法和贝叶斯反求方法。最大似然估计方法[5]是根据已知测量的统计信息，建立最大似然估计优化模型，以获取能够以较高概率产生测量数据的反求参量。为了充分利用先验信息，Tarantola[6]在贝叶斯框架下较为系统地探讨了模型参量识别的不确定性反问题理论和求解方法。Jiang等[7]发展了基于高斯过程模型的参量更新方法，增强了参量后验概率的可辨识性。但目前贝叶斯反问题的求解还依赖于计算耗时的马尔科夫链蒙特卡洛方法。为了克服不确定性反问题涉及的多层嵌套瓶颈，有效提高计算反求的效率和工程实用性，近年来基于不确定性传播和计算反求的解耦策略引起学者关注。Liu等[8,9]建立了面向任意概率分布的结构不确定性正向传播与反向识别统一框架，并将测量不确定性反问题转化为多个确定性反问题进行求解。另外，为了处理小样本、认知不确定性下的参量识别反问题，以非概率凸集度量为基础的计算反求方法有待发展。Jiang等[10]提出了区间反问题的概念和求解方法，实现了层合板结构材料特性参量的区间不确定性识别。Wang[11]考虑非精确信息发展了基于证据理论的结构参量识别方法。

对于模型不确定性反问题，不仅需利用已知测量信息和结构模型来实现未知参量的计算反求，而且还需要定量化分析结构建模本身的不确定性对反求参量的影响。由于求解过程的复杂性，目前关于模型不确定性反问题的研究相对较少。Du[12]提出了基于序列可靠性分析的不确定性反求方法，实现了建模不确定性下结构未知参量概率分布的有效估计。Liu等[13,14]利用随机结构之间的相似性，提出了基于相似系统分析和点估计的模型不确定性反问题高效求解方法，实现了模型参量的概率不确定性向反求参量的传播分析。Liu等[15]发展了区间不确定性结构的动态载荷识别方法，准确稳定地获取了载荷的不确定性边界。

事实上，对于实际工程问题中的结构参量反求，更为普遍的是测量不确定性和模型不确定性往往同时并存，这类问题在本文中称之为多源不确定性反问题。由于不同来源不确定性的耦合作用，以及反问题求解计算的复杂性等，导致很难探明多源不确定性在结构参量识别中的逆向传递机理，相关研究目前也鲜有报到。为此，本文针对实际工程中更为普遍存在的多源不确定性反问题进行探索性研究，特别是发展高效的基于混合度量和流形学习的多源不确定性计算反求方法，在实现未知结构参量识别的同时有效量化测量不确定性和模型不确定性对反求参量的综合影响，提高不确定性反问题的工程实用性。

2 不确定性反问题建模

从系统论的角度而言，结构参量识别反问题是利用已知的测量响应和正问题模型对未知的结构参量进行反求。对于实际工程结构，由于材料或载荷的随机性、制造或测量的误差以及物理过程认知不明晰等原因，在测量响应和正问题模型中往往存在各种不确定性因素。不确定性反问题的求解不仅需要实现结构参量的有效识别，而且还需定量化评估不同来源不确定性对参量识别结果的影响，因此是一个涉及结构参量计算反求和不确定性传播的双层嵌套复杂求解过程。根据不确定性在系统中出现位置的不同及对反求参量影响的不同，特别是双层嵌套求解机制的不同，可将结构参量识别的不确定性反问题分为测量不确定性反问题、模型不确定性反问题和二者并存的多源不确定性反问题。

2.1 测量不确定性反问题

结构测量响应不确定性来源于测量误差的统计或不确定性结构的统计响应。测量不确定性反问题可描述为利用已知的不确定性测量响应和确定性系统模型，对未知的结构参量进行识别，并评价测量不确定性对参量识别影响，其模型可表述为

(1)

式中Z和fZ(Z)为测量响应及其不确定性度量，X和fX(X)为待反求的结构参量及其不确定性度量，F为测量不确定性到反求参量不确定性之间的映射关系，g为结构正问题模型。

测量不确定性反问题的求解可通过不确定性传播分析和优化反求的迭代来实现。如图1所示，对于测量不确定性反问题涉及的双层嵌套求解过程，其内层为结构不确定性传播，即利用结构正问题模型实现从给定的fX(X)到计算响应不确定性的量化分析；其外层为优化反求过程，即对待反求参量的fX(X)进行优化，使计算响应与测量响应之间的不确定性度量达到匹配。

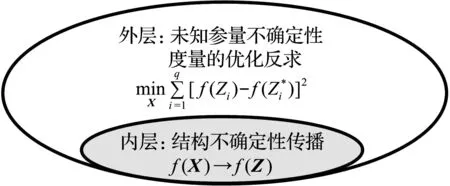
图1 测量不确定性反问题的嵌套求解

2.2 模型不确定性反问题

模型不确定性反问题中部分模型参量及其不确定性度量已知，如随机结构中参量概率分布已知，而部分模型参量未知，需通过有限的测量响应进行反求识别，并评估模型不确定性对反求参量的影响。鉴于此，模型不确定性反问题可表述为

(2)

式中U和fU为结构正问题模型中的不确定性参量及其度量。

事实上，在不确定性参量每一特定的蒙特卡洛采样下，结构正问题模型可认为是确定的，故可通过大量采样下的确定性反问题求解及反求参量的统计来实现模型不确定性反问题的求解。基于此思想，模型不确定性反问题也是通过不确定性传播分析和优化反求的迭代来实现，但其内外层结构与测量不确定性反问题相反。如图2所示，其内层为在特定不确定性参量样本点下，进行确定性计算反求获取相应未知参量的识别结果；其外层为利用不确定性传播分析方法，实现从模型参量不确定性度量到反求参量不确定性度量的量化分析。

图2 模型不确定性反问题的嵌套求解

2.3 多源不确定性反问题

对于工程中更为普遍的多源不确定性反问题，在实现未知结构参量反求的同时，需综合评价测量不确定性和模型不确定性对待参量识别结果的影响，其模型可表述为

(3)

式中fZ(Z)·fU(U)为测量和模型的联合不确定性度量，且两类不确定性相互独立。

通常结构响应可通过多次测量获取较为充足的响应样本，故本文采用概率模型来度量测量响应中的随机不确定性。结构建模过程存在一定的认知局限性，且难以获取复杂工程结构的模型样本，本文采用非概率多边凸集模型[14]来度量结构模型中的不确定性。如图3所示，以二维不确定性为例，根据少量样本点可以获得传统区间模型

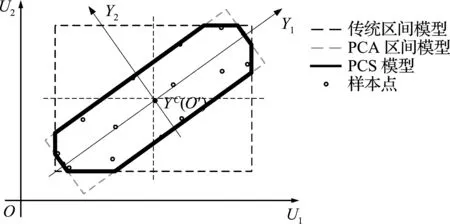
图3 多边凸集模型

U∈{ΩI|UL≤U≤UR}

(4)

式中UL和UR为不确定建模参量样本的上下界。对样本点数据进行主成分分析，得到特征向量PT，并将其作为样本数据空间的正交基底，即转换矩阵。以特征向量对应的基方向构成新的不确定性建模坐标系，并将样本数据向其投影，得到主成分PCA(Principal component analysis)区间模型

(5)

(6)

多源不确定性反问题求解的基本思想是将不确性反问题转化为确定性反问题，以实现测量及模型两类不确定性反问题的解耦。在多边凸集度量下，对于凸集不确定性模型参量每一特定的蒙特卡洛样本，结构正问题模型可视为是确定的，则多源不确定性反问题退化为测量不确定性反问题。在概率度量下，求解该测量不确定性反问题可获得反求参量的一条概率分布函数CDF(Probability distribution function)曲线。如图4所示，如遍历整个多边凸集模型采样，可获得一簇CDF曲线，进而可采用CDF曲线的边界即 P -box 模型来实现多源不确定性反问题识别结果的综合不确定性量化。

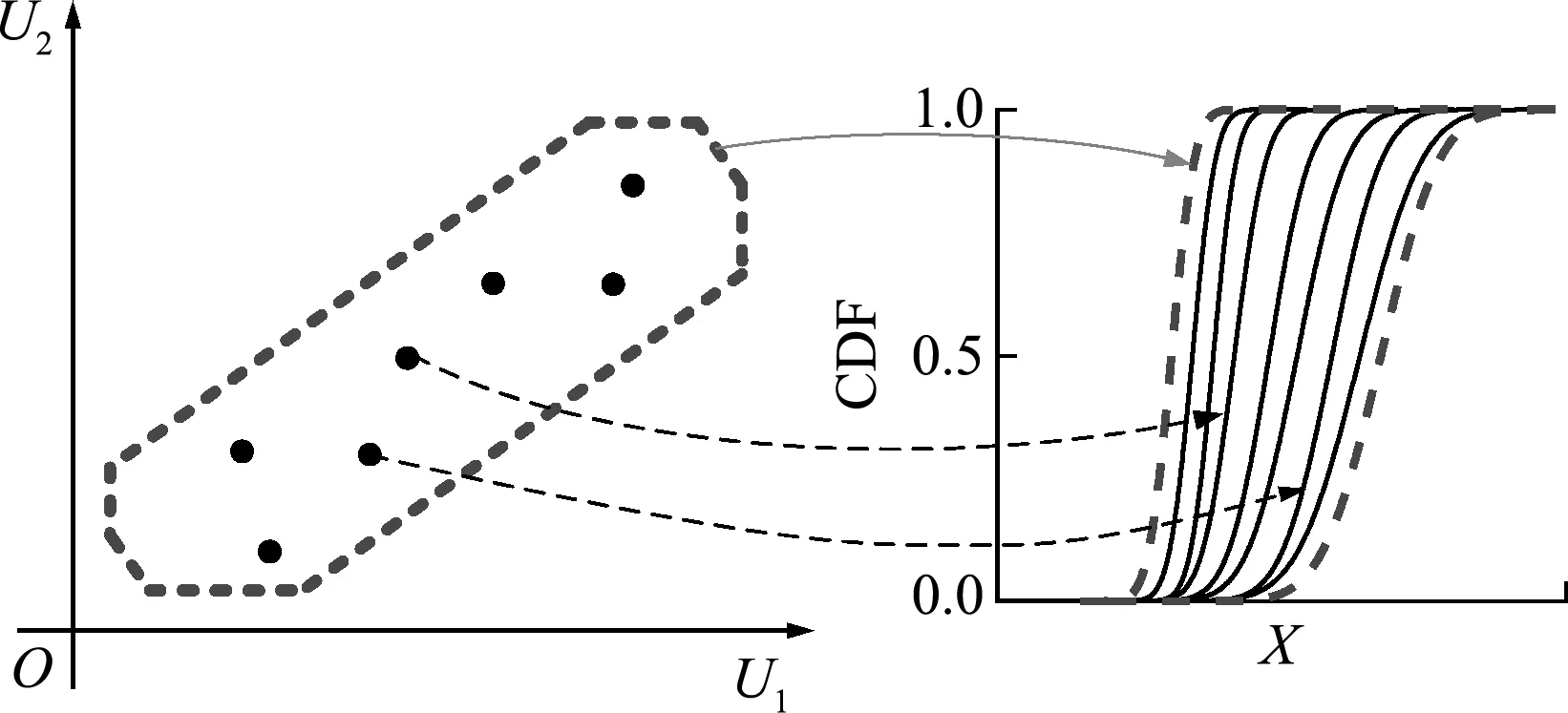
图4 不确定性模型参量与反求参量CDF间的映射

根据上述分析可知，如图5所示，多源不确定性反问题的求解是一个复杂的多层嵌套过程，涉及模型不确定性反问题和测量不确定性反求的耦合，并存在迭代求解计算量大的瓶颈问题。

图5 多源不确定性反问题求解策略

3 基于CDF流形学习的多源不确定性反求方法

由于不确定性模型参量的多边凸集模型中任意一个样本点都与反求参量的 P -box 模型中的一条CDF曲线对应，如能构建出二者之间映射关系，则有望快速遍历整个多边凸集模型的采样，获取反求参量的 P -box 模型。基于此思想，本文提出基于CDF流形学习的多源不确定性反问题高效求解方法。该方法通过建立不确定性模型参量与反求参量CDF间的流形学习映射模型，实现测量响应不确定性反问题与模型不确定性反问题的解耦，从而将多源不确定性反问题转化为少数几个测量不确定性反问题，进而将测量不确定性反问题通过降维积分方法又转化为了少数几个确定性反问题，以此解决多源不确定性反问题多层耦合嵌套导致的计算量大的难点问题。

3.1 不确定参量与反求参量的CDF流形学习映射

本文方法的重点是建立不确定性模型参量与高维反求参量CDF曲线之间的映射关系。为此，将流形学习方法引入映射模型构建中，将高维CDF曲线转化为流形空间的低维特征参数，通过建立模型参量与低维特征参数之间的代理模型，实现给定模型参量下反求参量CDF的快速预测。

在多边凸集模型内对不确定性模型参量进行最优拉丁超立方抽样，获取m个样本点。对于每一样本点，进行测量不确定性反问题求解，可获得与之相对应的m条待反求参量CDF曲线。统一将每组CDF曲线进行离散，则可获得离散维矩阵H。

H=[h1,h2,…,hm]T

(4)

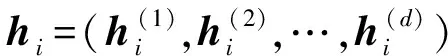
(5)

对协方差矩阵C进行特征值分解，并将特征值按由大到小的顺序排列。在保证CDF流形学习映射模型精度的情况下，舍弃贡献较小的特征值，实现数据降维，即取前k(k≪d)阶特征值和对应的特征向量。

通过上述分析，可将d维的高维问题转化为k维的低维问题进行处理，通过低维流形空间中特征向量的线性组合可近似重新构建高维的反求参量CDF，实现给定模型不确定性参量U下对应的反求参量CDF曲线离散向量的快速预测，即

(6)

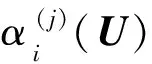
3.2 基于降维积分的测量响应不确定性反求

3.1节通过流形学习方法将多源不确定性反问题转化为少数几个测量不确定性反问题，本节将利用基于衍生的λ-PDF降维积分方法进一步将测量不确定性反问题转化为少数配置点处的确定性反问题。

对于测量不确定性反问题，待反求参量的概率密度函数PDF(Probability density function)形式未知，即其PDF可能为任意形式。为此，本文采用二阶衍生的λ-PDF[18]对未知反求参量的不确定性进行建模，

f(x|b0,b1,b2,λ)=

(7)

κ=Γ(λ+1)/[Γ(0.5)Γ(λ+0.5)]

(8)

式中b0,b1和b2为衍生的λ-PDF的控制参数，Γ(·)为伽马函数。如图6所示，二阶衍生的λ-PDF可以参数化地表示未知的任意概率密度曲线。

图6 不同λ下衍生的λ-PDF

可通过匹配计算响应与测量响应的统计矩来反求未知参量的PDF，故基于前四阶矩的测量不确定性反问题的目标函数可表示为

(9)

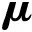
(10)

(11)

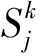
(12)

其可以通过二项式定理递推求解

(13)

(14)

基于此，原系统的统计矩分解为子系统的统计矩进行计算，从而有效提高了不确定性传播效率。

在实现正向不确定性传播后，利用优化算法对式(9)进行迭代求解，可实现λ-PDF控制参数的有效反求，进而通过式(7)得到与测量响应概率特征最相匹配的待反求参量的CDF曲线。

3.3 多源不确定性反问题求解流程

本文提出的基于流形学习的多源不确定性反问题求解流程如图7所示。

图7 多源不确定性反问题求解流程

(1) 获取结构不确定性测量响应的概率密度函数和模型参量不确定性的多边凸集模型。

(2) 在多边凸集内对模型参量进行最优拉丁超立方采样。

(3) 对于每个模型参量样本点，利用降维积分和优化算法进行测量不确定性反问题求解，获取待反求参量的CDF曲线。

(4) 对步骤(3)获取的CDF曲线进行流形分析，得到低维流形空间的特征向量和特征参数。

(5) 利用步骤(2)模型参量的样本点和步骤(4)低维流形空间的特征参数，建立径向基函数代理模型，并实现从模型参量到反求参量CDF的流形学习映射关系建模。

(6) 基于流形学习映射模型对多边凸集模型中模型参量的蒙特卡洛样本进行反求参量CDF预测，并统计获取反求参量的 P -box 模型。

4 算例分析

4.1 数值算例

考虑如下的数值模型

(14)

式中Z1和Z2为已知的测量响应，分别服从正态分布N(9,1.6)和N(23,2.6)；U1和U2为不确定性模型参量，采用如图8所示的多边凸集模型对其不确定性进行度量；X1和X2为待反求参量。

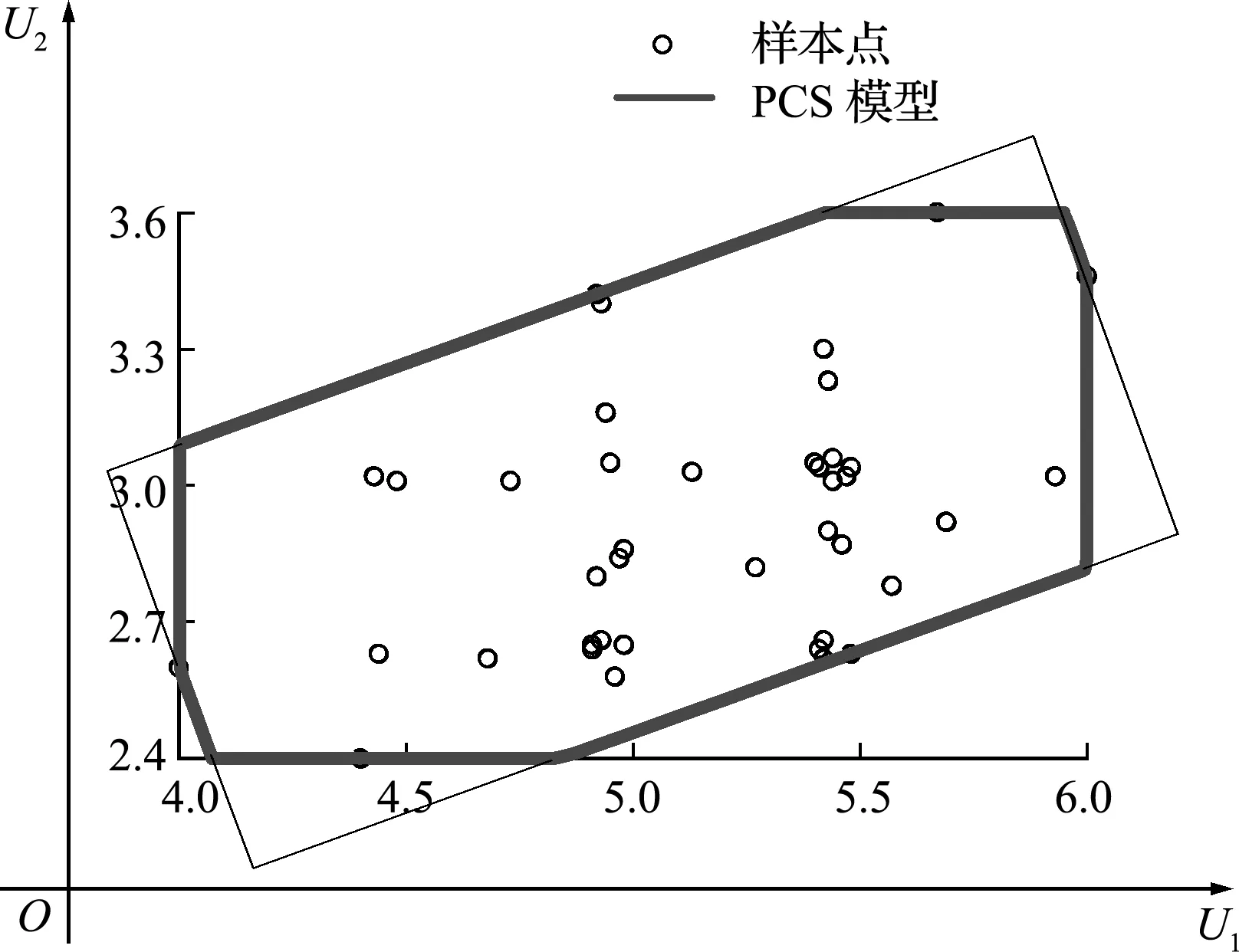
图8 模型参量样本点和多边凸集模型

在不确定性模型参量多边凸集域内进行最优拉丁超立方采样，生成40个样本点。在每个样本点下通过基于降维积分的不确定性反求方法进行测量响应不确定反问题求解，获得40条反求参量的CDF曲线。将高维的CDF离散数据进行流形分析，将其转化为低维流形空间中的特征参数和特征向量，并建立不确定性模型参量与待反求参量CDF之间的流形学习映射模型。为验证流形学习映射模型准确性，图9给出了4个模型参量测试样本点下直接预测的CDF曲线与计算反求的CDF曲线。由对比结果可知，流形学习映射模型获得的CDF与计算反求获得CDF几乎一致，可用该映射模型直接替代耗时的测量不确定性反问题求解过程。

在流形学习映射模型基础上，通过蒙特卡罗仿真MCS(Monte Carlo simulation)实现多边凸集度量下模型不确定性反问题的统计求解，快速获得了待反求参量X的 P -box 边界。为进一步验证该方法的准确性，在MCS产生的每一模型参量样本点进行测量不确定性反问题求解，获取待反求参量的 P -box 边界，两种方法的反求结果如图9所示。根据对比结果可得，本文提出的基于流形学习的多源不确定性反求方法的反求结果与MCS方法的反求结果基本一致，验证了本文提出方法的准确性。

图9 反求结果对比

4.2 涡轮叶片热力学参数的不确定性识别

航空发动机涡轮叶片和气体的对流换热系数对涡轮叶片的温度场分布有很大的影响，因此，有效识别对流换热系数对涡轮叶片冷却系统设计及叶片寿命评估具有重要影响[16]。本算例通过测量叶片表面应力来反求叶片压力面和吸力面与空气之间的对流换热系数。考虑到应力测量结果和涡轮叶片建模的多源不确定性，采用本文提出的不确定性反求方法对流换热系数进行识别。

图10所示为涡轮叶片的有限元分析模型，其中两个实心点为应力测量点。叶片热力学参数不确定性识别对应的正问题模型可表示为

图10 涡轮叶片有限元模型

σ=g(h1,h2,ε,λ)

(16)

式中σ=[σ1,σ2](MPa)为两个测点处的应力，分别服从N(671,1)和N(156.84,2)的正态分布。热膨胀系数ε(10-61/K)和导热系数λ(W/(m·K))为不确定性模型参量，对应的多边凸集模型如图11所示。h1和h2分别为压力面和吸力面上的对流换热系数，为待识别的未知参量。

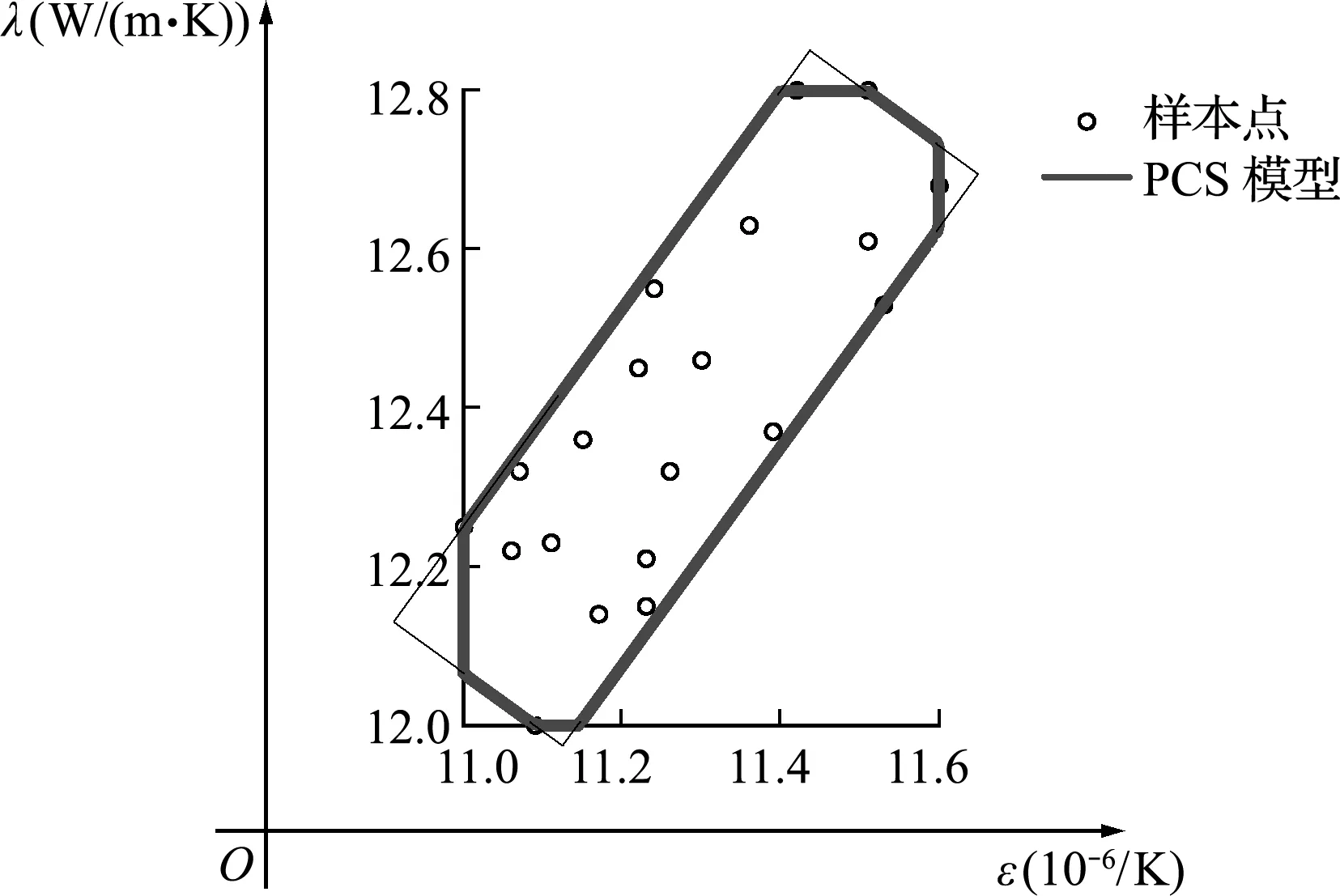
图11 参数h1和h2多边凸集模型

在模型参量多边凸域内随机抽取20个样本点，在每个样本点处利用基于降维积分的反求方法实现测量不确定性反问题求解，获得相应的识别参量的CDF曲线。利用流形学习方法，构建模型参量与反求参量CDF之间的映射模型，将热力学参数的多源不确定性反问题转化为流形学习映射模型下的不确定性传播问题。通过蒙特卡罗方法对度量模型参量的多边凸集不确定性向反求参量不确定性进行传播分析，获得涡轮叶片热力学参数 P -box 边界。反求结果如图12所示，由反求得到的 P -box 模型可知，压力面的对流换热系数大致分布范围在[52,70] W/(m2·K)区间内，吸力面的对流换热系数分布在[35,48] W/(m2·K)，另外图中CDF对比曲线再次验证了本文提出方法的准确性。

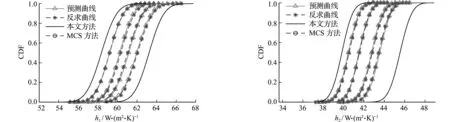
图12 反求的对流换热系数 P -box

5 结 论

本文针对多源不确定性反问题中面临多层耦合嵌套及大规模计算的难点问题，提出了基于概率-非概率混合度量和流形学习的多源不确定性高效计算反求方法。该方法通过建立模型参量与反求参量CDF之间的流形学习映射模型，以少量的计算成本实现了未知参量的 P -box 模型的高效反求。在反求过程中，通过流形学习实现了测量响应不确定性反问题与模型不确定性反问题的解耦，将多源不确定性反问题转化为少数几个测量不确定性反问题；进一步对于测量不确定性反问题，通过降维积分方法又转化为了少数几个确定性反问题，从而克服了多源不确定性反问题求解过程多层嵌套导致的反求效率和精度问题，在实现参量识别的同时综合量化了测量不确定性和模型不确定性对反求参量的综合影响。

参考文献(References):

[1] Han X,Liu J.NumericalSimulation-BasedDesign[M].Springer Press,2020.

[2] Elishakoff I,Fang T,Sarlin N,et al.Uncertainty quantification and propagation based on hybrid expe -rimental,theoretical,and computational treatment [J].MechanicalSystemsandSignalProcessing,2021,147:107058.

[3] Luo Y J,Kang Z,Li A.Structural reliability assessment based on probability and convex set mixed mo -del[J].Computers&Structures,2009,87(21-22):1408-1415.

[4] Wu D,Gao W,Song C M,et al.Probabilistic interval stability assessment for structures with mixed uncertainty [J].StructuralSafety,2016,58:105-118.

[5] Fonseca J R,Friswell M I,Mottershead J E,et al.Uncertainty identification by the maximum likelihood method [J].JournalofSoundandVibration,2005,288(3):587-599.

[6] Tarantola A.Popper,Bayes and the inverse problem [J].NaturePhysics,2006,2(8):492-494.

[7] Jiang Z,Apley D W,Chen W.Surrogate preposterior analyses for predicting and enhancing identifiability in model calibration[J].InternationalJournalforUncertaintyQuantification,2015,5(4):341-359.

[8] Liu J,Meng X H,Xu C,et al.Forward and inverse structural uncertainty propagations under stochastic variables with arbitrary probability distributions [J].ComputerMethodsinAppliedMechanicsandEngineering,2018,342:287-320.

[9] Meng X H,Liu J,Cao L X,et al.A general frame for uncertainty propagation under multimodally distributed random variables [J].ComputerMethodsinApp-liedMechanicsandEngineering,2020,367:113109.

[10] Jiang C,Liu G R,Han X.A novel method for uncertainty inverse problems and application to material characterization of composites[J].ExperimentalMe-chanics,2008,48(4):539-548.

[11] Wang C.Evidence -theory-based uncertain parameter identification method for mechanical systems with imprecise information[J].ComputerMethodsinApp-liedMechanicsandEngineering,2019,351:281-296.

[12] Du X P.Inverse simulation under uncertainty by optimization [J].JournalofComputingandInformationScienceinEngineering,2013,13(2):021005.

[13] Liu J,Hu Y F,Xu C,et al.Probability assessments of identified parameters for stochastic structures using point estimation method [J].ReliabilityEngineering&SystemSafety,2016,156:51-58.

[14] Cao L X,Liu J,Xie L,et al.Non-probabilistic polygo -nal convex set model for structural uncertainty quantification[J].AppliedMathematicalModelling,2021,89:504-518.

[15] Liu Y R,Wang L,Qiu Z P,et al.A dynamic force reconstruction method based on modified Kalman filter using acceleration responses under multi-source uncertain samples [J].MechanicalSystemsandSignalProcessing,2021,159:107761.

[16] Abu A O,Eshati S,Laskaridis P,et al.Aero -engine turbine blade life assessment using the Neu/Sehitoglu damage model [J].InternationalJournalofFatigue,2014,61:160-169.