例析导数解题中的若干“陷阱问题”

广东省惠州市第一中学 (516007) 余 军 方志平

导数在高中数学的学习当中是十分重要的,导数也为函数问题的求解带来了新的视角，但由于学生对导数中一些概念理解不清，而造成解题错误的现象是屡见不鲜的.在平常的教学中，我们要注意研究易错的知识点和加强对易错问题的反思，尤其是要对“形似质异”的导数问题多加甄别.本文通过对几例导数中的“陷阱问题”加以剖析，旨在唤起大家的注意.

1.导数在解决有关函数极值问题上的陷阱

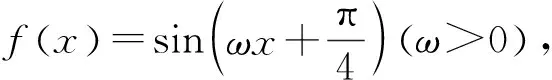
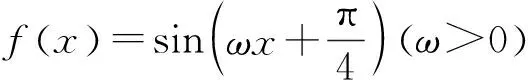
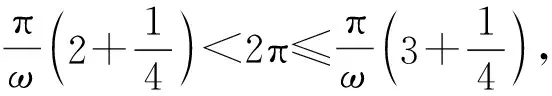
评注：函数极值、极值点的定义：如果函数f(x)在点x=x0的一个邻域(x0-δ,x0+δ)内有定义，对任意的x∈(x0-δ,x0)∪(x0,x0+δ),总有f(x)f(x0)，则称f(x0)为函数f(x)的极小值，x0称为函数f(x)的极小值点.可见函数的极值f(x0)是与x0“附近”的左、右两边函数值进行比较而得知.所以极值点只能落在区间的内部，不能落在区间的端点处.

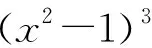
A.x=1 B.x=0 C.x=-1 D.x=-1、0或1

错解：由f′(x)=6x5-12x3+6x，令f′(x)=0，解得极值点为x1=-1,x2=0,x3=1.故选择D.

评注：使导数值为0的点不一定是极值点.如，常见的函数y=x3，在x=0处导数值为0，但x=0并不是该函数的极值点.是否为极值点，这需要根据极值点的定义进行判别.

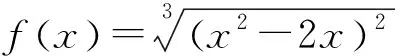
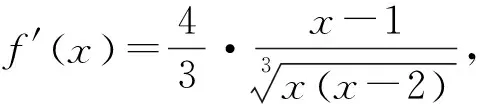
陷阱：函数f(x)在定义域内不可导的点为x1=0,x2=2.当x变化时，f′(x)的变化情况如下表：

x-∞,0 00,1 11,2 22,+∞ f'x -不存在+0-不存在+

所以x1=0,x2=2是函数f(x)的两个极小值点，函数f(x)的极小值为f(0)=f(2)=0.从而函数f(x)的极大值为1,极小值为0.

评注：对任意函数来说，极值可能在定义域内导数为0处取得，也可能在函数不可导处取得.

例4 函数f(x)=x3+ax2+bx+a2在x=1时有极值为10,那么a+b的值为( ).

A.-7 B.0

C.-7或0 D.以上都不对

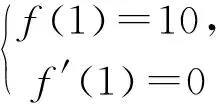
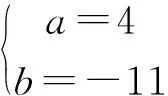
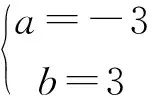
评注：对于可导函数在极值点处导数值一定为0，但导数值为0的点未必是极值点.

2.导数在解决有关函数单调性问题上的陷阱

例5 已知函数f(x)=x3-mx2+2m2-5(m<0)的单调递减区间是(-9,0)，求实数m取值的集合.

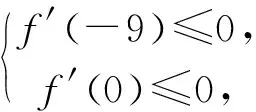
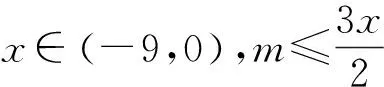
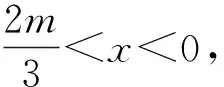
评注：“函数f(x)在区间(a,b)单调递减”，与“函数f(x)单调递减区间是(a,b)”，这是两个不同的概念.前者中的区间(a,b)不一定是函数的单调递减区间，但一定是单调递减区间的子区间；后者是指函数“在且仅在”区间(a,b)上单调递减.

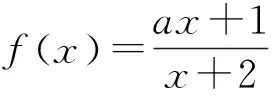
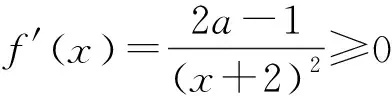
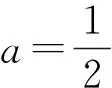
评注：对于(a,b)内可导函数，f′(x)≥0是函数f(x)单调递增的必要不充分条件；而f′(x)>0是函数f(x)单调递增的充分不必要条件.

3.导数在解决有关函数图象切线问题上的陷阱

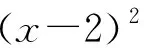
错解：直线C1的斜率为k=y′=2x，C2为k=y′=-2x+4，从而2x=-2x+4,解得x=1,于是直线l的斜率为k=2,所以直线l与C1的切点是(1,1)，与C2的切点是(1,-1)，由点斜式方程得切线方程为2x-y-1=0和2x-y-3=0.

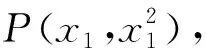
评注：直线l是曲线C1、C2的公切线，切线是同一条，但切点不一定是同一个，因此，如果建立斜率相等的方程2x=-2x+4,就等于承认切点是相同的了，这显然是不严谨的.

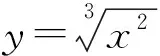
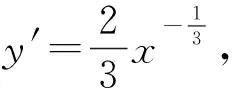
评注：一些学生误认为斜率不存在，切线就不存在.其实函数在某点处可导，则其图象在该点处必有切线，反之，若函数图象在某点处有切线，则函数在该点处不一定可导.

例9 求曲线f(x)=3x-x3过点A(2,-2)的切线方程.

错解：∵点A在曲线f(x)=3x-x3上，且f′(x)=3-3x2，∴f′(2)=3-3×22=-9,故所求切线方程为y+2=-9(x-2),即9x+y-16=0.

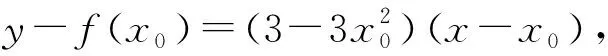
评注：曲线“在某点处的切线”是指过该点且以该点为切点的切线,从而该点也必须是曲线上的点；“过某点的切线”则不一定以此点为切点,该点也不一定在曲线上,因此所求切线可能不止一条.

通过对上述易错点的诊断，我们不难发现，审题不清、概念模糊或受思维定式的影响，常常会使学生落入题目设计的“陷阱”中去，这也提醒我们，在解决与导数有关的问题时，要重视对基本概念和题意的理解.