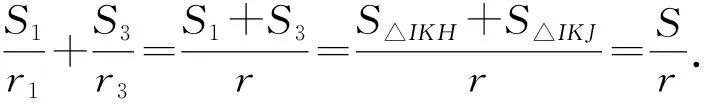圆外切四边形涉及旁切圆的一个性质
2021-09-06江苏省运河高等师范学校221300颖江苏省苏州工业园区工业技术学校215000胡甲维
中学数学研究(江西) 2021年8期
江苏省运河高等师范学校 (221300) 胡 颖江苏省苏州工业园区工业技术学校 (215000) 胡甲维
圆外切四边形有许多优美的性质,本文给出的是与它内切圆和四个旁切圆相关的一个性质.

图1
如图1所示,圆外切四边形ABCD,与四边形的一边及它的两条相邻边的延长线都相切的圆称为四边形的一个旁切圆,共有四个旁切圆.旁切圆的三个切点构成的三角形称为这个旁切圆的切点三角形.四边形的内切圆与各边的切点构成的四边形称为切点四边形.设四个旁切圆半径依次是r1,r2,r3,r4,相对应的四个切点三角形面积依次为S1,S2,S3,S4,内切圆半径为r,切点四边形面积为S,则有如下性质:
为了证明上面这个性质,首先证明一个引理.


图2
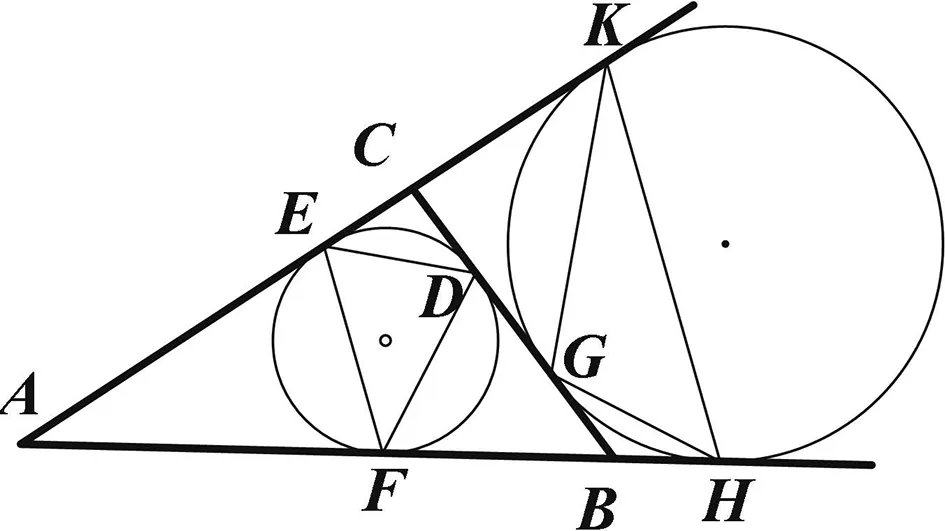
图3
为了证明上面的引理,先给出并证明下面几个结论.
结论1 如图3,两个切点三角形分别是△DEF和△GHK,则有∠EDF+∠HGK=180°.当然也有sin∠EDF=sin∠HGK.


图4

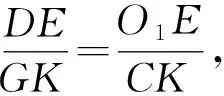
结论3O1B·O1C=O1O2·r1,
O2B·O2C=O1O2·r2.

图5
证明:如图5,不难看出O1,B,O2,C四点共圆,则∠O1O2C=∠O1BD,由此得O1B·O1C=O1B·O1O2·sin∠O1O2C=O1O2·O1B·sin∠O1BD=O1O2·O1D=O1O2·r1,同理可证O2B·O2C=O1O2·r2.

有了上面的引理,证明本文的性质就容易了.我们分两种情形来说明.
情形1:圆外切四边形的两组对边分别交于一点.
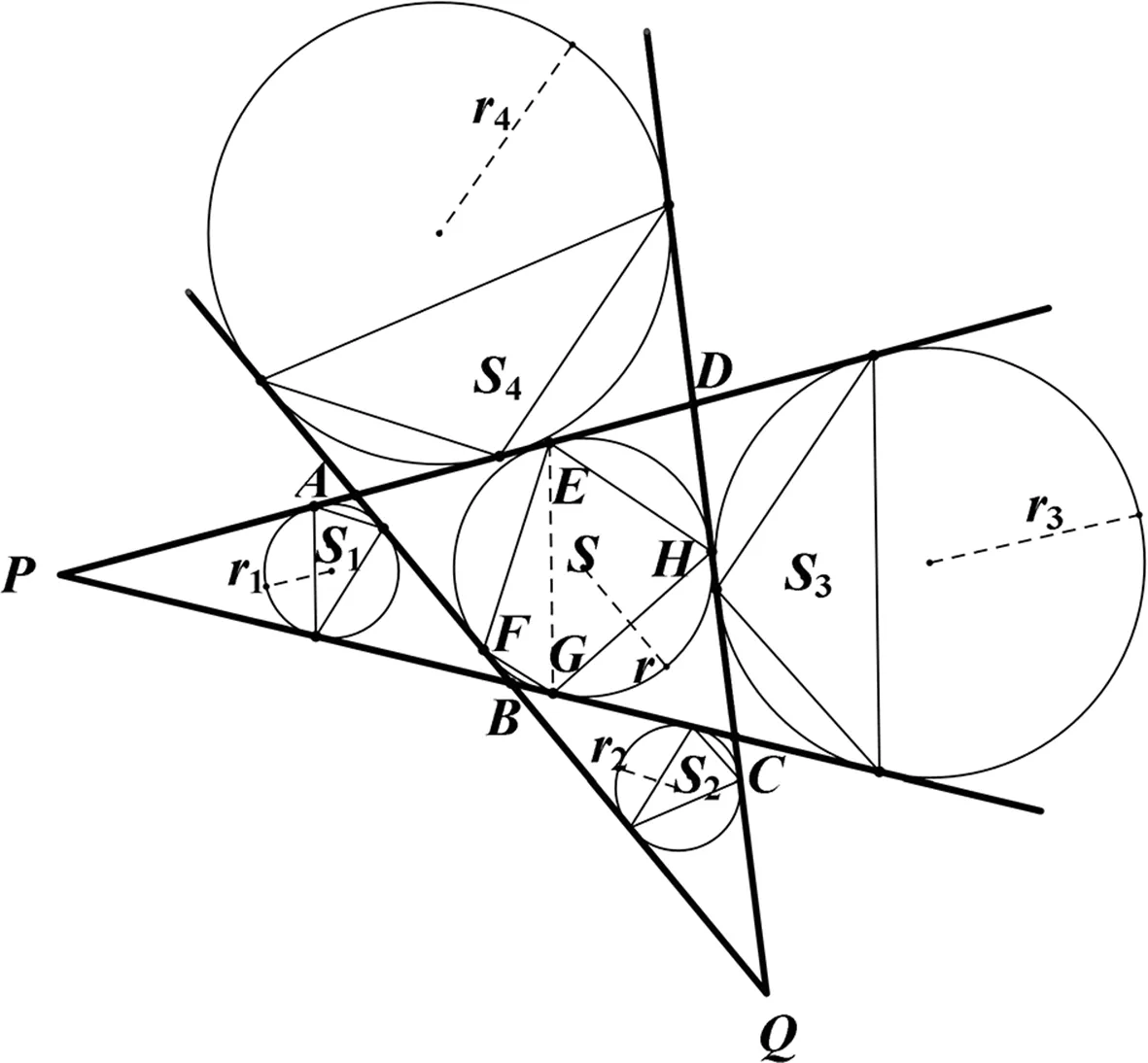
图6

情形2:圆外切四边形的两组对边有一组对边平行或两组对边分别平行.

图7