基于双耦合电感高增益二次型Boost变换器

田东豪，荣德生

(辽宁工程技术大学电气与控制工程学院，辽宁 葫芦岛 125105)

1 引言

近年来，光伏、风能等可再生能源发展迅速，其核心部件高增益DC-DC变换器备受关注。理想的Boost电路理论上在极限占空比的情况下可以达到很高的增益，如果占空比工作在接近于1的极限状态下，输出二极管的导通时间极短，将会导致严重的反向恢复和电磁干扰问题，而且由于电路寄生参数的存在，升压增益特性受限[1-3]。因此高稳定性、高增益、高效率的DC-DC变换器受到国内外学者的广泛关注。

传统的Boost变换器一般采用倍压单元[4]、开关电容(Switched Capacitor，SC)[5,6]或开关电感[7]、电压乘法单元(Voltage Multiplier Cell,VMC)、级联等方式提高电压增益。针对传统Boost变换器电压增益受限的问题，文献[8-14]提出了一系列基于耦合电感的高增益非隔离直流变换器，通过合理地设计耦合电感的匝比，变换器可以获得很高的电压增益。但存在漏感能量利用率低、开关管电压尖峰高、漏感和开关管寄生电容谐振等问题。文献[15]在基于耦合电感Boost变换器的基础上通过添加无源钳位电路和有源钳位电路，用以吸收漏感能量，减少电路谐振现象，从而提出了一系列具有钳位电路的耦合电感Boost变换器。但输出二极管电压应力高的问题没有得到改善。文献[16]提出了一种耦合电感高增益双管升压变换器，该变换器具有电压增益大及开关管电压电流应力低的特点，但该结构使用了两个开关管，增加了控制的复杂度。

文献[17]提出了单管高增益Boost变换器，所提变换器具有控制难度低、二极管电压应力低等优点，但输出功率较低，仅为38 W，且由于使用一个耦合电感，电压增益受限。文献[18]采用了双耦合电感的结构，进一步提升电压增益、减小二极管电压应力，但引入了一组二极管电容无源吸收回路，增加了电路的复杂度。本文受文献[17，18]的启发，对其提出的拓扑进行改进，提出了一种基于双耦合电感高增益二次型Boost变换器，在变换器输入端采用两级Boost，并引入两个耦合电感倍压单元，两个耦合电感副边串联，以提高变换器的电压增益。与输出端共用二极管和电容实现无源吸收回路，抑制了开关管电压尖峰，同时提高了电路的功率密度。文中详细分析了所提变换器的工作原理和工作特性，并制作了一台180 W、18 V/180 V的实验样机，验证了理论分析的正确性。

2 工作原理分析

2.1 电路拓扑

图1(a)为双耦合电感Boost高增益DC-DC变换器拓扑，电路由输入电源Vin，耦合电感L1、L2，电容C1、Co1、Co2、Co3,二极管VD1、VD2、VDo1、VDo2和VDo组成。图1(b)为拓扑等效电路，耦合电感L1、L2等效为由励磁电感Lm1、Lm2，漏感Lk1、Lk2和匝比为np1:ns1、np1:ns2的理想变压器构成，假设n=ns1/np1=ns2/np2。输出二极管VDo和输出电容Co1构成无源吸收电路，当开关管S关断后，耦合电感L1原边的漏感Lk1通过VD2向电容C1释放能量；耦合电感L2原边的漏感Lk2通过二极管VD2向电容Co1释放能量，从而提升了漏感能量的利用率。VDo、VDo1、VDo2为输出二极管，Co1、Co2、Co为输出滤波电容，C1为中间储能电容，Ro为负载电阻。为简化分析，提出如下假设：

(1)开关管S和二极管VD1、VD2、VDo1、VDo2、VDo为理想器件。

(2)电容C1、Co1、Co2、Co3的容值足够大，其端电压保持恒定。

(3)设两个耦合电感的耦合系数k相等，并且设k=Lm/(Lm+Lk)。

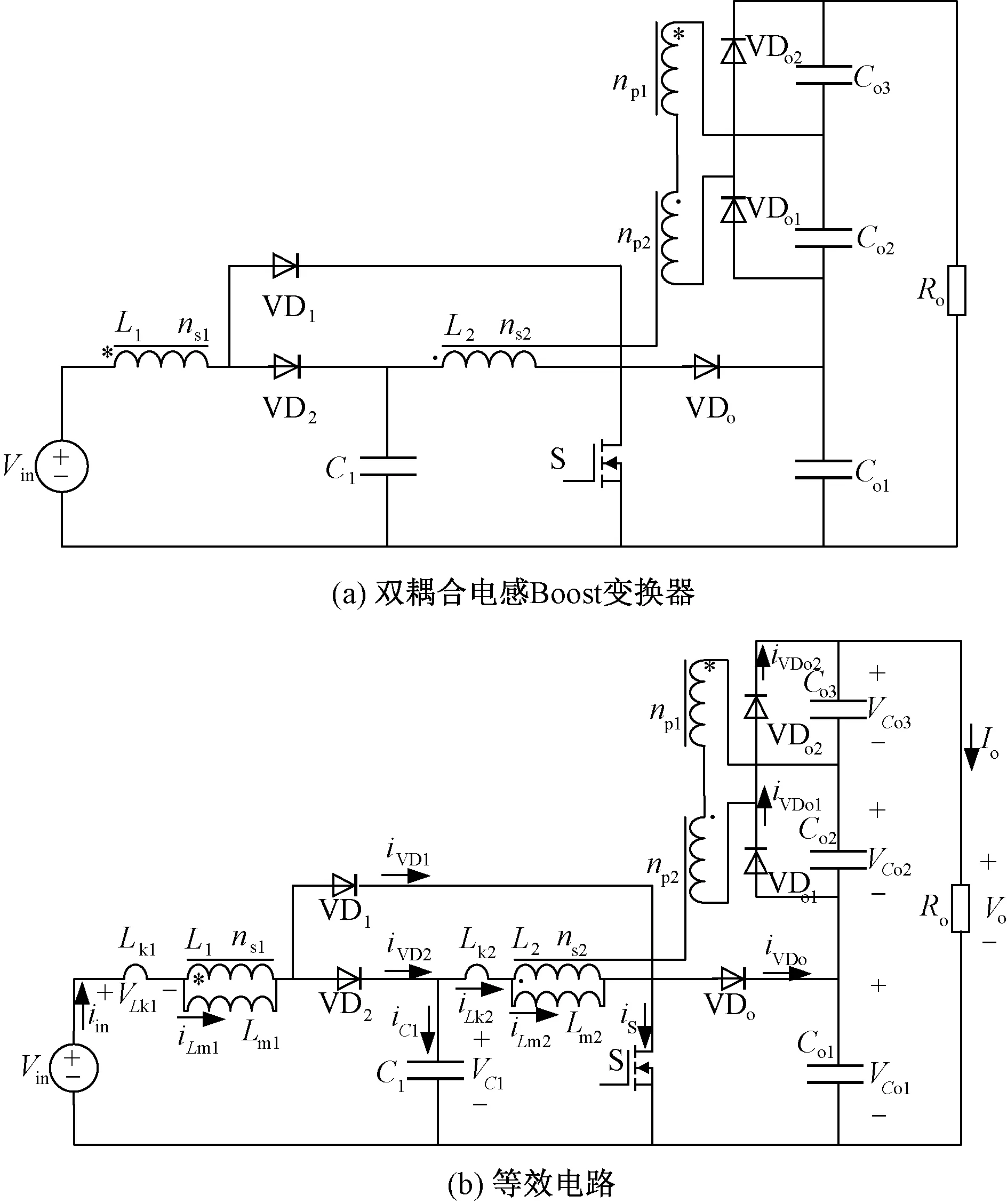
图1 所提变换器拓扑结构Fig.1 Proposed converter topology

2.2 连续工作模态分析

假设励磁电感Lm1和励磁电感Lm2的电流均连续，即工作在连续工作模式(Continuous Conduction Mode,CCM)。如图2为该变换器工作在CCM下的关键工作波形，在一个开关周期内，该变换器存在如图3所示的5种工作模态。

图2 变换器的主要波形图(CCM)Fig.2 Main waveforms of converter (CCM)

模态Ⅰ[t0～t1]：如图3(a)所示，开关管S处于导通状态，二极管VD1和VDo1因承受正向压降导通，二极管VD2、VDo2和输出二极管VDo关断。输入电压作用在励磁电感Lm1上，励磁电感Lm1储能，励磁电感电流iLm1线性上升。电容C1通过开关管S给励磁电感Lm2储能，电感电流iLm2线性上升。耦合电感L1的漏感电流即输入电流线性上升。耦合电感副边串联给输出电容Co2充电，输出电容Co1、Co2和Co3串联给负载供电。当开关管S关断时，此模态结束。在此阶段，根据基尔霍夫电压定律，iLm1、iLm2和iin可以表示为：

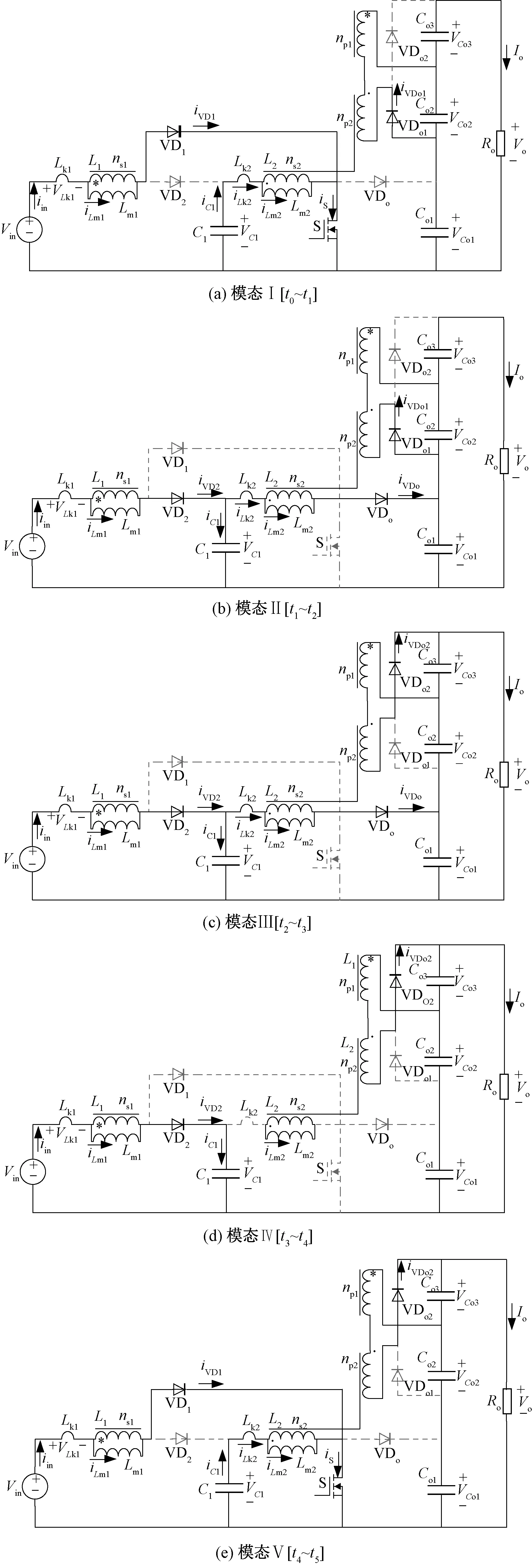
图3 所提变换器各个工作模态等效电路图(CCM)Fig.3 Equivalent circuits of switching modes(CCM)

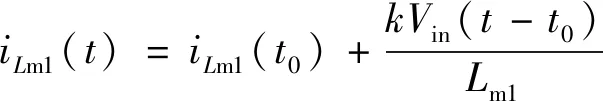
(1)

(2)

(3)

模态Ⅱ[t1～t2]：如图3(b)所示，t1时刻，二极管VD1关断。为提供耦合电感L1原边线圈的电流通路，二极管VD2和VDo因承受正向电压而开通，二极管VDo1和VDo2维持上一模态状态不变。输入电压Vin、励磁电感Lm1和漏感Lk1串联给电容C1充电，漏感Lk2的能量释放给输出电容Co1，耦合电感副边串联继续给输出电容Co2充电。由于此模态过程极短，可认为励磁电感电流基本不变。二极管VDo1承受反向电压关断时，此模态结束。

模态Ⅲ[t2～t3]：如图3(c)所示，开关管S保持关断，二极管VDo1关断，为提供耦合电感副边线圈的电流通路，二极管VDo2因承受正向电压而导通；二极管VD1和VD2维持上一模态状态不变。输入电压Vin和耦合电感L1的原边串联给中间电容C1充电。输出二极管VDo导通，输入电源Vin、耦合电感L1原边和耦合电感L2原边经过VDo给输出电容Co1充电。同时漏感电流iLk1向C1释放，iLk2向Co1释放，输出电容Co3通过励磁电感副边储能。励磁电感电流iLm1和iLm2线性下降。输出电容Co1、Co2和Co3串联为输出负载供电。输出二极管VDo电流下降，当iVDo=0时，VDo自然关断，此模态结束。励磁电感Lm1和Lm2的电流表示如下：

(4)

(5)

模态Ⅳ[t3～t4]：如图3(d)所示，t3时刻，二极管VDo实现零电流关断，其余二极管维持上一模态状态不变。漏感Lk2的能量释放完毕，励磁电感Lm2能量通过耦合电感传递到副边，励磁电感电流iLm1和iLm2继续线性下降。输入电源和耦合电感L1原边串联给电容C1充电，耦合电感副边串联给输出电容Co3充电。输出电容Co1、Co2和Co3串联为输出负载供电。直到下一个开关周期驱动脉冲的到来，此模态结束。

模态Ⅴ[t4～t5]：如图3(e)所示，t4时刻，驱动信号VGS加在开关管S的两端，开关管S导通。二极管VD1和VDo2因承受正向压降而导通。二极管VD2、VDo1和VDo关断。当开关管S导通时，输入电压作用在耦合电感L1原边，电容C1释放能量给耦合电感L2原边。励磁电感电流iLm1和iLm2线性上升，副边通过二极管VDo2给输出电容Co3充电，输出电容Co1、Co2和Co3串联给负载Ro提供能量，当二极管VDo2因承受反向电压而关断时，此模态结束。

2.3 非连续工作模态分析

当励磁电感Lm1电流连续，Lm2的电流断续，电路工作在连续-非连续工作模式(Continuous Conduction Mode-Discontinuous Conduction Mode,CCM-DCM)模式下；当励磁电感Lm1和Lm2的电流均断续，电路工作在DCM-DCM下。在一个开关周期内，所提变换器在CCM-DCM下存在5个工作模态，图4为变换器工作的主要波形，各个模态的等效电路如图5(a)～图5(e)所示。

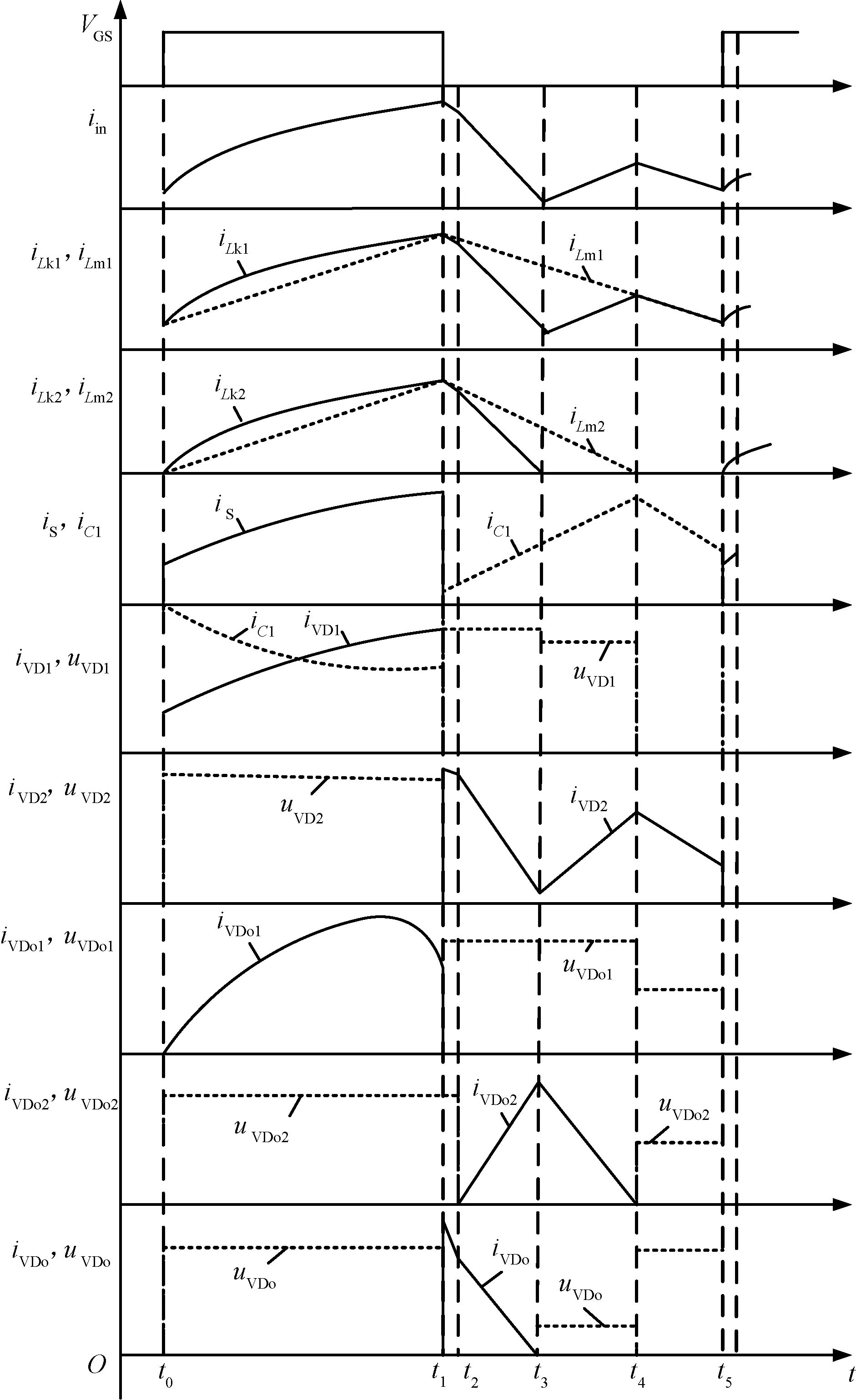
图4 变换器的主要波形图(DCM)Fig.4 Main waveforms of converter (DCM)

模态Ⅰ[t0～t1]：如图5(a)所示，在t0时刻，开关管S开通，二极管VD1和VDo1导通，二极管VD2和VDo2关断，输出二极管VDo关断。电源电压加在耦合电感L1原边Lm1上，耦合电感L2原边电压VLm2等于C1两端电压。电流iLm1和iLm2线性上升。耦合电感副边串联给Co2充电。当开关管S关断时，此模态结束。

模态Ⅱ[t1～t2]：如图5(b)所示，在t1时刻，开关管S关断，二极管VDo、VD2和VDo1导通，二极管VD1和VDo2关断。漏感电流和励磁电感电流缓慢下降。耦合电感副边给电容Co2充电。电容C1和Co1吸收漏感能量。负载能量由输出电容Co1、Co2和Co3串联提供。此模态持续时间极短，当二极管VDo1关断，二极管VDo2导通时，此模态结束。

模态Ⅲ[t2～t3]：如图5(c)所示，开关管S保续关断，二极管VDo2导通，二极管VDo1关断，其他二极管状态与上一模态相似。耦合电感L1和L2原边漏感电流快速下降，漏感能量继续被电容C1和Co1吸收，耦合电感副边串联给输出电容Co3储能，原边励磁电流iLm1和iLm2线性下降，当耦合电感L2原边漏感电流iLk2降至零时，此模态结束。

模态Ⅳ[t3～t4]：如图5(d)所示，在t3时刻，开关管保持关断，漏感Lk2的能量已经释放完毕。二极管VD2和VDo2保持导通，二极管VD1、VDo1和VDo截止。输入电流即励磁电感Lm1的电流线性下降，且电压为k(Vin-VC1)，电容Co3继续充电储能。当励磁电感Lm2中的电流iLm2为零时，此模态结束。

模态Ⅴ[t4～t5]：如图5(e)所示，在这个模态中，励磁电感Lm2电流为零，耦合电感L1的漏感电流iLk1和励磁电感电流iLm1相等。二极管VD2导通，开关管S和二极管VD1、VDo、VDo1、VDo2均关断，VD2中的电流线性下降。电容C1充电储能。负载能量由输出电容Co1、Co2和Co3串联提供。当开关管S导通时，此模态结束，下一周期开始。

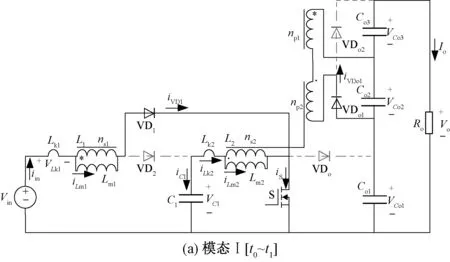
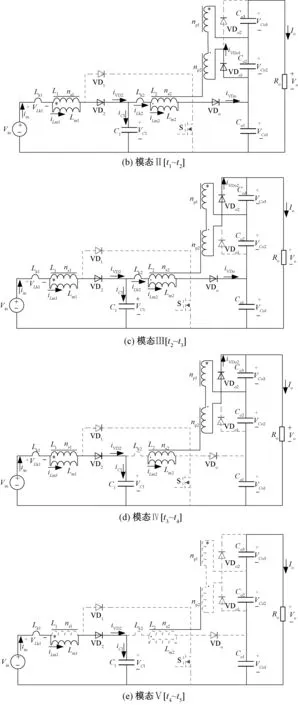
图5 所提变换器各个工作模态等效电路图(DCM)Fig.5 Equivalent circuits of switching modes(DCM)

3 变换器稳态性能分析

3.1 CCM工作模态模式

为了便于稳态分析，忽略过渡模态Ⅱ和Ⅴ，仅讨论分析模态Ⅰ、模态Ⅲ和模态Ⅳ。假设耦合电感的耦合系数相同且为k，耦合系数k为：

(6)

假设耦合电感的匝比相同且为n，匝比n可以表示为：

(7)

当变换器工作在模态Ⅰ时，根据图3(a)，有：

(8)

(9)

(10)

当变换器工作在模态Ⅲ时，由图3(c)有：

(11)

(12)

(13)

当变换器工作在模态Ⅳ时，由图3(d)有：

(14)

(15)

对耦合电感L1、L1原边励磁电感Lm1和励磁电感Lm2使用伏秒平衡原理，有：

(16)

(17)

结合式(8)、式(11)、式(14)和式(16)得到电容C1的电压为：

(18)

根据式(10)可以得到Co2的电压为：

(19)

由式(9)、式(12)、式(14)、式(15)和式(17)可以得到Co1的电压为：

(20)

根据式(13)可以得到Co3的电压为：

(21)

结合式(19)～式(21)可以得到输出电压Vo的表达式为：

(22)

根据式(22)可以得到变换器工作在CCM下的电压增益表达式为：

(23)

根据式(23)可知，变换器的电压增益和耦合电感的匝比n、耦合系数k有关。图6是变换器电压增益和耦合电感匝比n、耦合系数k的关系曲线。从图中可以看出，耦合电感匝比n越大，变换器的电压增益越高；而随着两耦合电感漏感的增加，所提变换器的电压增益有一定的减小，故在实际设计中，应尽可能地使耦合电感紧耦合。

为了简化分析，令耦合电感耦合系数k=1，忽略漏感对变换器的影响。此时变换器的电压增益为：

(24)

开关管S的电压应力为：

(25)

二极管VD1和VD2的电压应力为：

(26)

(27)

二极管VDo的电压应力为：

(28)

二极管VDo1和VDo2的电压应力为：

(29)

3.2 DCM临界条件

假设励磁电感Lm1的电流连续，励磁电感Lm2电流断续，即工作在CCM-DCM下。并假设所提变换器为理想变换器，有：

VoIo=VinIin

(30)

对于励磁电感Lm1工作在CCM下需满足以下条件：

2ILm1>ΔiLm1

(31)

式中，ILm1为励磁电感Lm1的电流平均值；ΔiLm1为励磁电感Lm1的电流纹波。

ILm1可以表示为：

(32)

励磁电感Lm1的电流纹波可以表示为：

(33)

假设等效电感时间常数τLm1表示为：

(34)

由式(30)～式(34)可以得到励磁电感Lm1电流连续的临界条件为：

(35)

当τ<τLm1时，变换器工作在CCM-DCM模式。

假设模态Ⅲ持续的时间为DX，模态Ⅳ持续的时间为DY。在每一个开关周期中，二极管VDo的平均值可以表示为：

(36)

二极管VDo2的电流平均值可以表示为：

(37)

假设输出电容Co1、Co2、Co3足够大，则可以认为在变换器稳定工作时流过输出电容的电流为零，所以可近似认为IVDo1、IVDo2、IVDo三者电流相等。根据式(36)和式(37)可以得到：

(38)

(39)

设开关管的开关频率为fs，励磁电感Lm2的时间常数τLm2可以表示为：

(40)

图7展示了当耦合电感匝比n=1时，所提变换器励磁电感Lm1和Lm2的电流临界连续的时间常数与占空比D的关系。当τ>τLm2时，变换器工作在CCM-CCM模式；当τLm1<τ<τLm2时，变换器工作在CCM-DCM模式；当τ<τLm1时，变换器工作在DCM-DCM模式，即流过励磁电感Lm1和Lm2的电流断续。

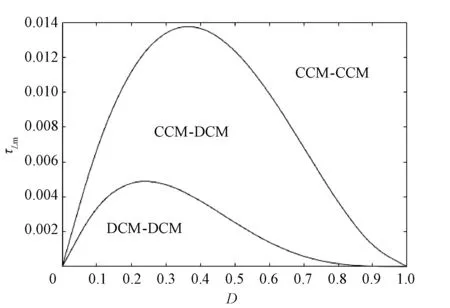
图7 临界等效电感时间常数与占空比D的关系曲线图Fig.7 Relationship between critical parallel equivalent inductance time constant and duty cycle D

3.3 变换器性能对比

将本文所提变换器与文献[17-19]所提变换器的各项性能指标进行对比，各项参数对比见表1。本文所提变换器当匝比n=1，k=1时，开关管S的电压应力仅为输出电压的2/5，具有开关管电压应力低的优点。

表1 不同变换器性能参数Tab.1 Different converter performance parameters

在匝比n固定的情况下，给定耦合电感匝比n=1，变换器的增益对比曲线如图8所示。从图8中可以看出，当n和k固定的情况下，所提变换器的电压增益明显更高。

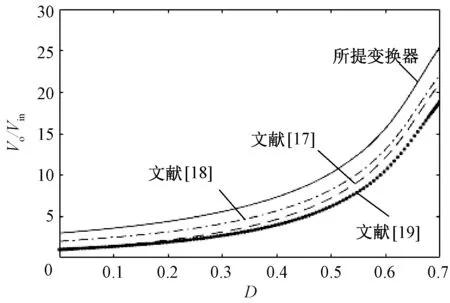
图8 变换器增益对比曲线Fig.8 Converter gain comparison curves

图9为变换器开关管电压应力对比曲线，尽管在占空比大于0.4的时候文献[19]比所提变换器的开关管电压应力小，但在相同增益的情况下，所提变换器仍比文献[19]开关管电压应力小。

图9 变换器开关管电压应力对比曲线Fig.9 Comparative converter switch voltage stress curves

4 实验结果与分析

为验证本文所提出的高增益DC-DC变换器原理的正确性，制作了一台试验样机以验证理论分析的正确性，主电路的主要参数见表2。实验样机如图10所示。

表2 主电路参数Tab.2 Main circuit parameters

图10 试验样机Fig.10 Experimental prototype

图11为变换器的输入输出电压波形，可以看出，变换器实现了输入18 V，输出180 V的高增益变换。图12为开关管S的电流波形及电压波形图。图13为两个耦合电感漏感Lk1和Lk2的电流波形图。

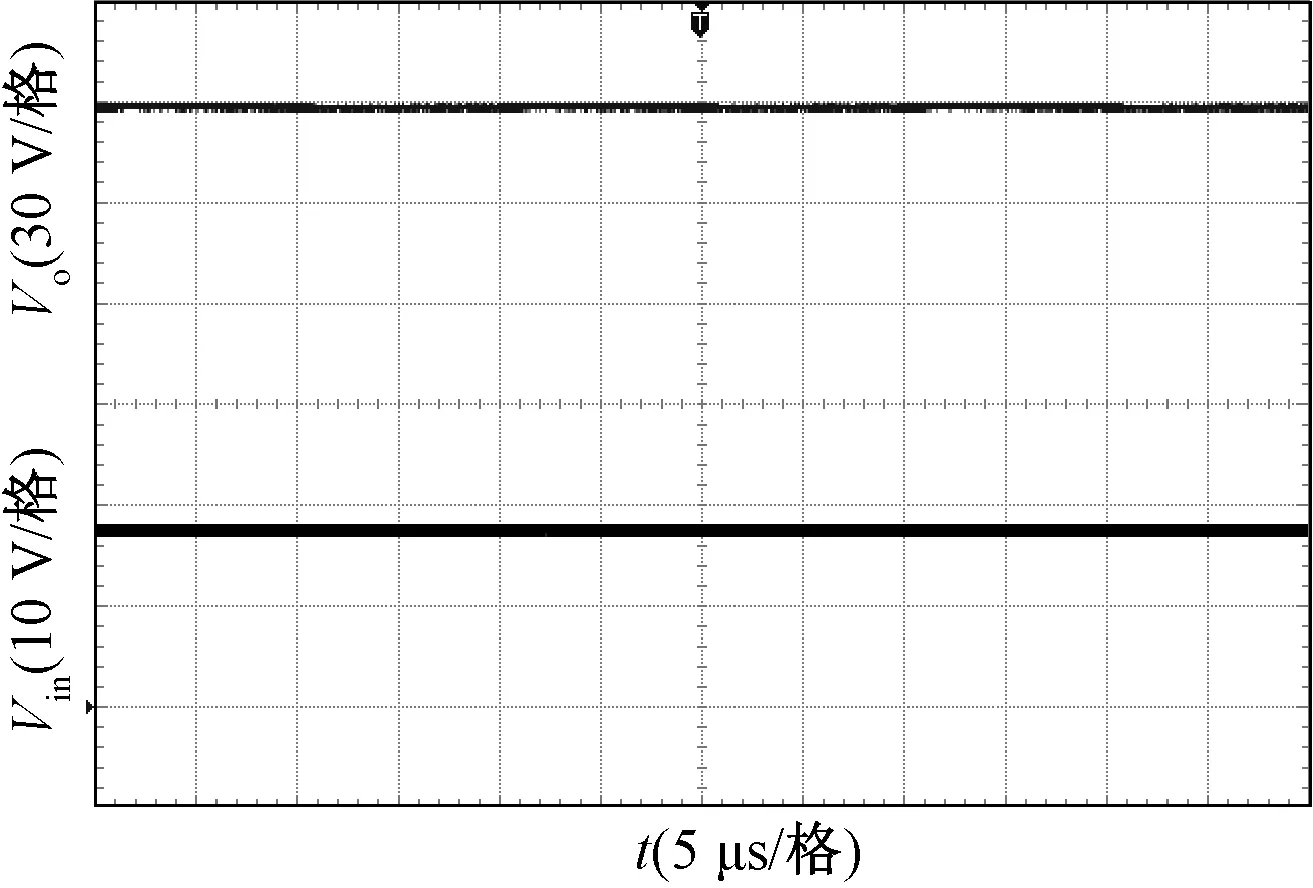
图11 Vin,Vo波形Fig.11 Waveforms of Vin and Vo

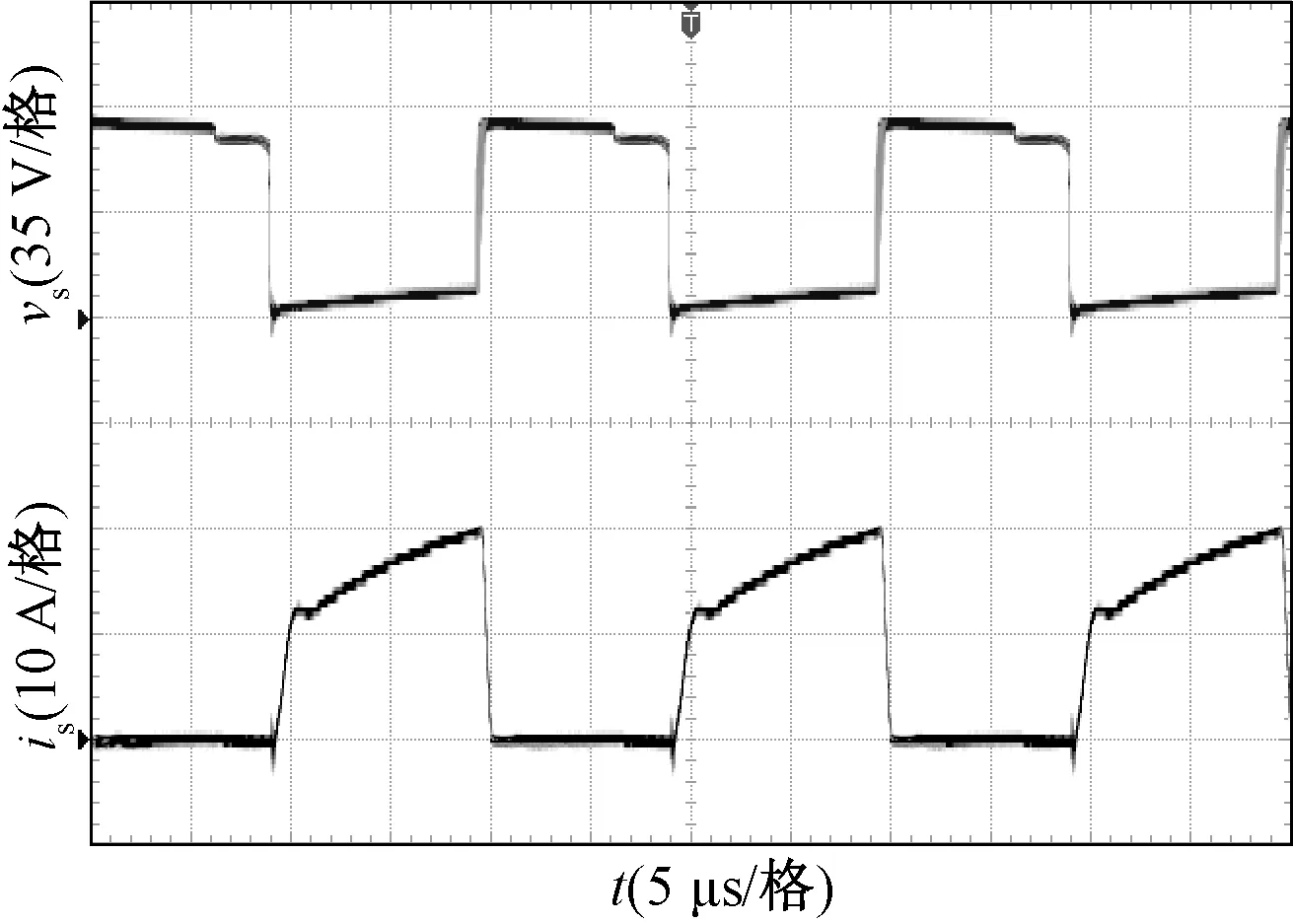
图12 开关管S的电流和电压波形Fig.12 Waveforms of us and is

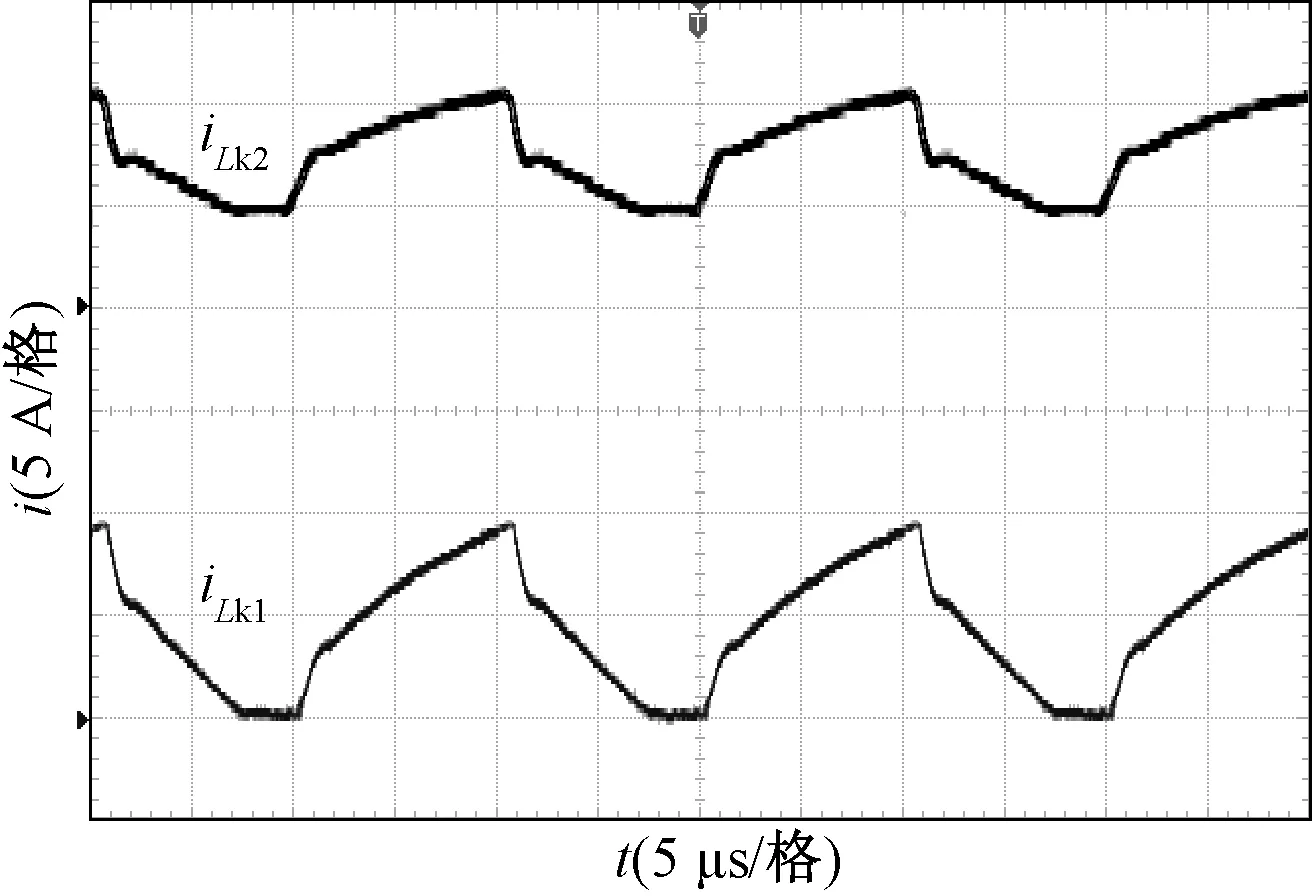
图13 Lk1和Lk2的电流波形图Fig.13 Waveforms of iLk1 and iLk2

图14为输出二极管VDo电流和电压波形图，VDo的电压约为80 V低于输出电压。图15和图16分别为二极管VD1和VD2的电流和电压波形图，两个二极管的电压约为40 V。图17和图18分别为输出二极管VDo1和VDo2的电流和电压波形图，两个输出二极管的电压约为90 V，电流约为3 A。

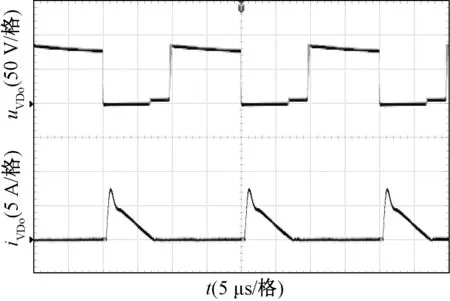
图14 二极管VDo的电压和电流波形Fig.14 Waveforms of uVDo and iVDo

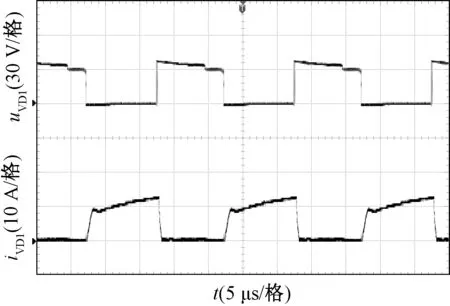
图15 二极管VD1的电压和电流波形Fig.15 Waveforms of uVD1 and iVD1

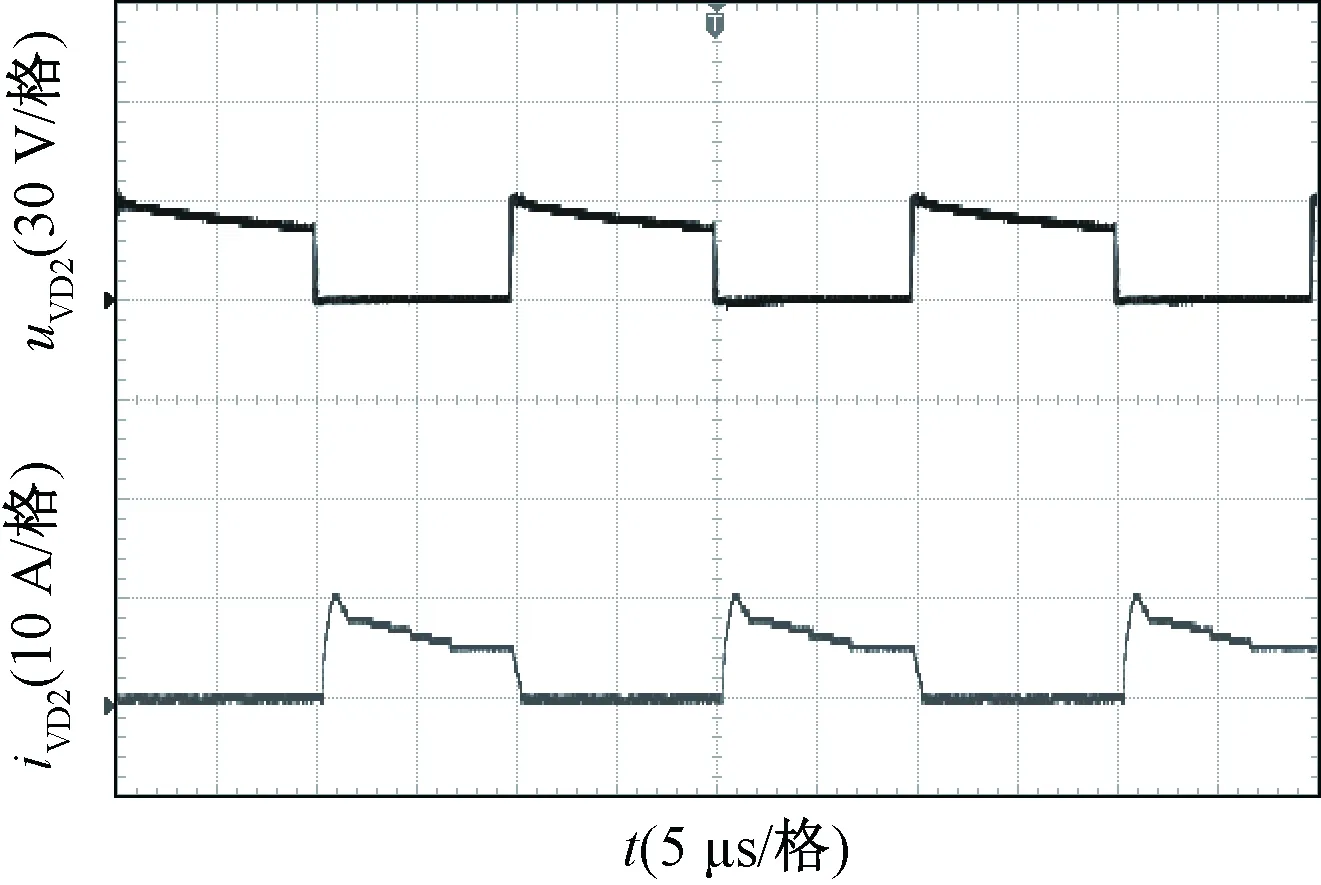
图16 二极管VD2的电压和电流波形Fig.16 Waveforms of uVD2 and iVD2

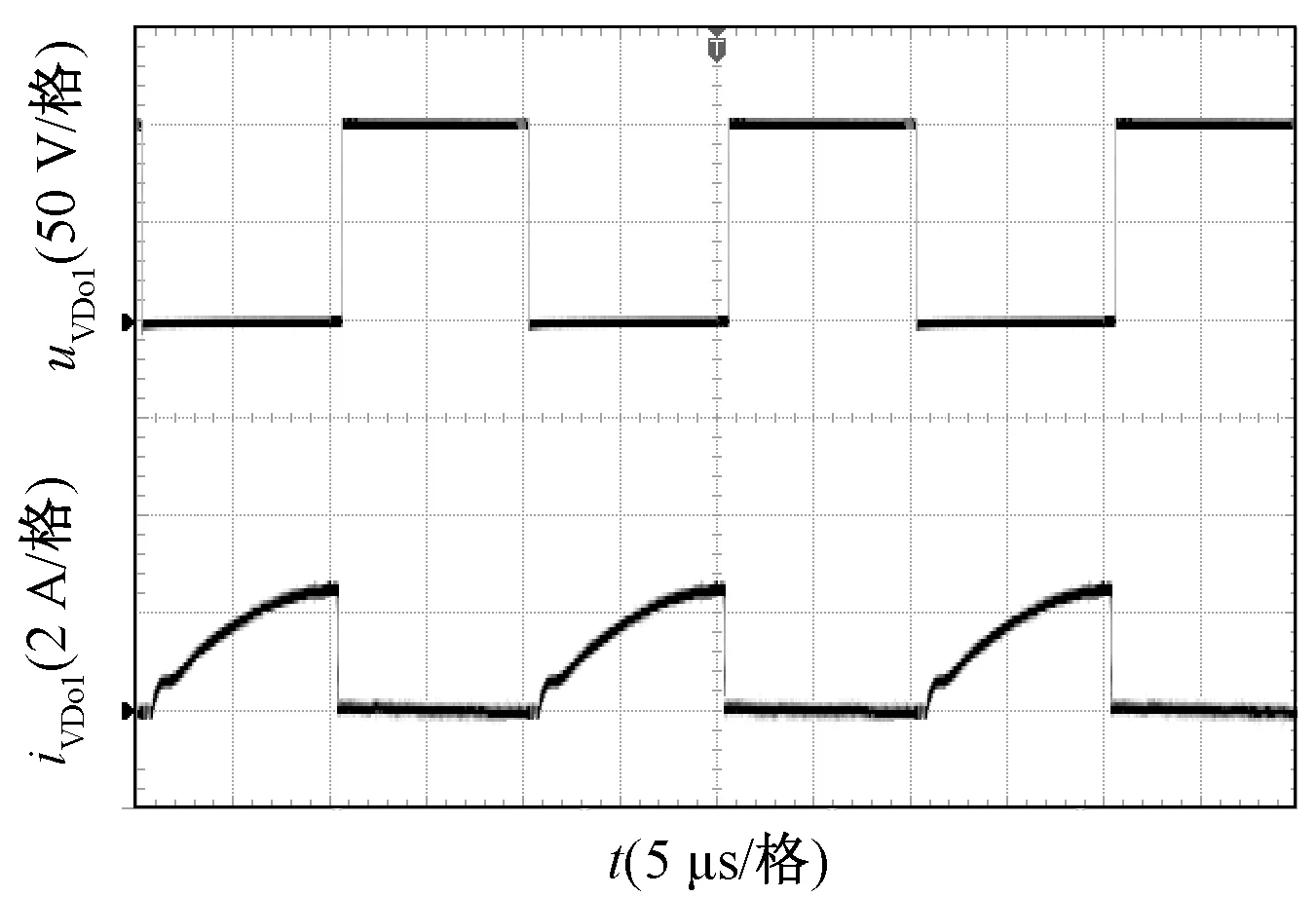
图17 二极管VDo1的电压和电流波形Fig.17 Waveforms of uVDo1 and iVDo1

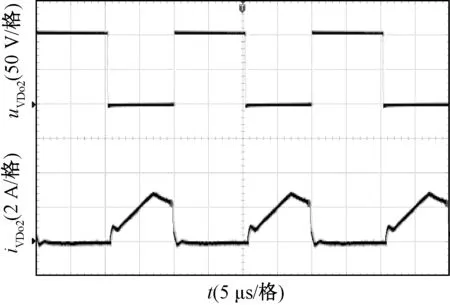
图18 二极管VDo2的电压和电流波形Fig.18 Waveforms of uVDo2 and iVDo2

为进一步证明所提变换器高增益和二极管低电压应力等特点，将输入电压设置为12 V，测得其耦合电感漏感电流波形、开关管电压波形、二极管VDo1、VD1、VD2电压和输入输出波形，如图19所示。从图19中可进一步验证本文所提拓扑理论的正确性。

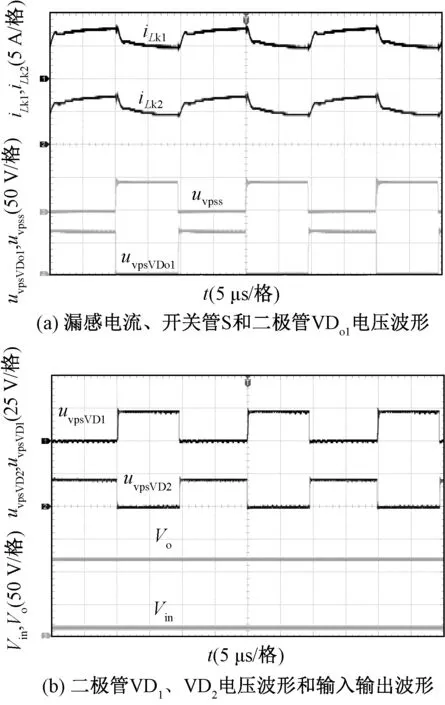
图19 Vin=12 V时关键波形图Fig.19 Waveforms of Vin=12 V

图20为所提变换器在180 V输出不变的情况下，效率随输出功率变化的曲线。当输出功率为90 W时，输出功率最大，最大效率为94%，在额定功率180 W条件下效率可达92.5%。

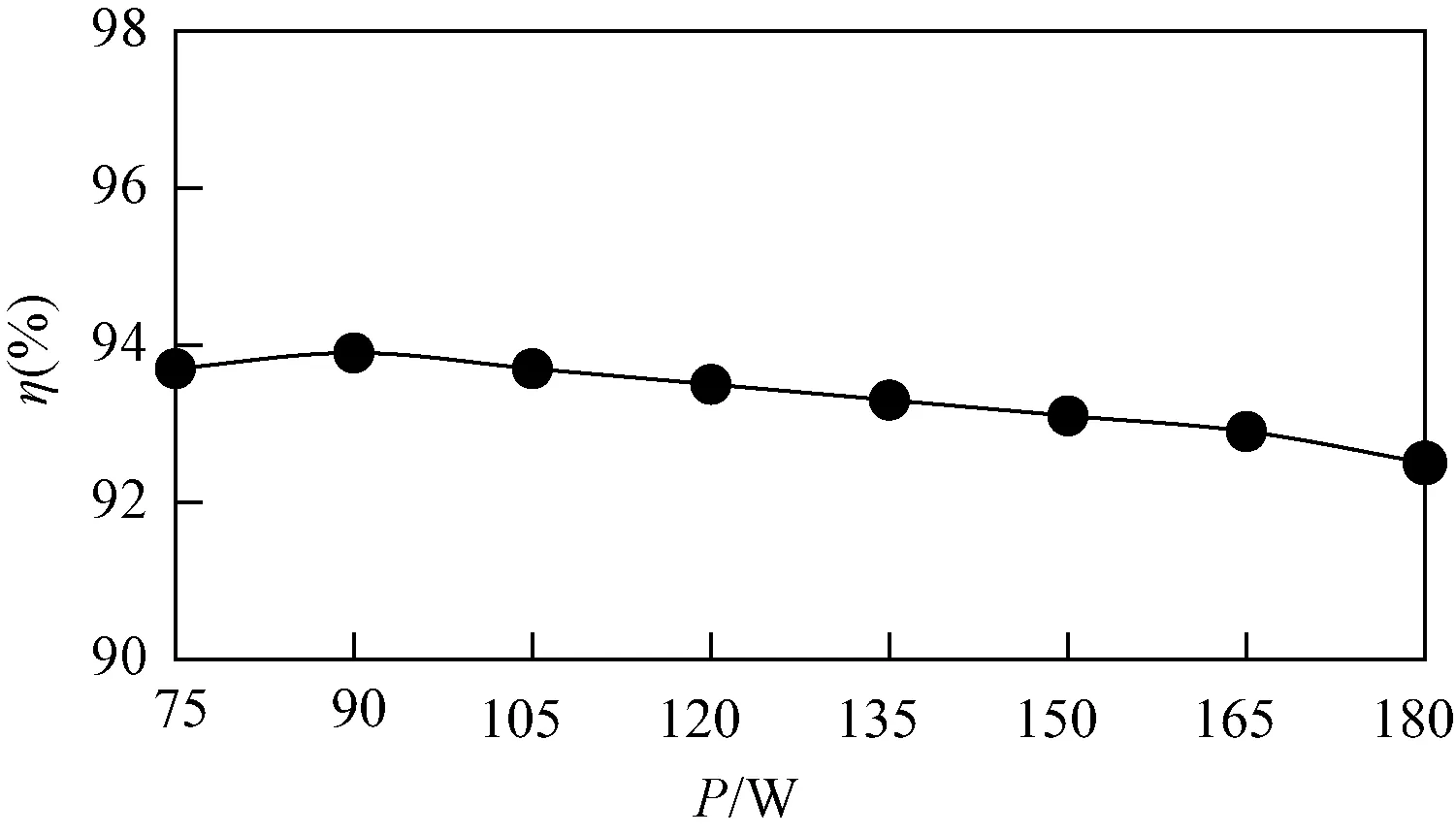
图20 效率曲线Fig.20 Efficiency curve

5 结论

为进一步提升DC-DC变换器的增益，提出了一种双耦合电感非隔离高增益变换器拓扑，分析了其CCM-CCM、CCM-DCM和DCM-DCM状态下的工作原理，与传统的直流变换器相比，具有如下优点：

(1)在相同占空比下，所提拓扑具有更高的电压增益，更低的开关管电压应力，且使用单管控制，降低了控制的复杂度。

(2)输出电容和输出二极管同时作为无源吸收回路，充分利用漏感能量，提高变换器的功率密度。

(3)对于双耦合电感结构，可以通过调节占空比D和耦合电感匝比灵活调节变换器的电压增益，有效地避免变换器工作在极限占空比的情况。