电动汽车充电用LCL型PWM整流器输出阻抗分析及稳定性改善方法
2021-08-31曾四鸣李秉宇杜旭浩崔顺尧杜庆诚肖国春
常 征,曾四鸣,李秉宇,杜旭浩,崔顺尧,杜庆诚,肖国春
(1.国网河北省电力有限公司,河北 石家庄 050021;2.国网河北省电力有限公司电力科学研究院,河北 石家庄 050000;3.国网河北省电力有限公司辛集市供电分公司,河北 石家庄 052300;4.西安交通大学电气工程学院,陕西 西安 710049)
1 引言
随着电动汽车的普及、续航里程的增加以及政策引导,人们对大功率快速充电的需求越来越强烈[1,2]。为了适应大功率充电的需要,必须保证充电系统在不同负荷以及不同负荷切换时系统稳定运行。大功率电动汽车充电系统一般主要由输入(前级)PWM整流器与输出(后级)DC/DC变换器组成[3],是一个典型的交直流混合级联系统。充电系统中独自稳定运行的各个交流与直流模块在(交流或直流)公共节点连接后可能因为模块间的相互作用导致系统不能稳定运行[4,5],进而对电网、电池及充电系统带来不利影响和危害。
电动汽车充电系统是典型的电力电子级联系统,包括PWM整流器组成的源变换器和DC/DC变换器组成的负载变换器。与建立系统稳态模型由零极点分布研究稳定性方法相比,阻抗法通过各模块端口阻抗特性研究负载变换器接入对系统稳定性的影响,简化分析过程[6-8]。目前大多数文献是基于Middlebrook准则,利用模块端口的阻抗特性来分析系统的稳定性[9],若在系统工作的整个频率范围内,当源变换器的输出阻抗小于负载变换器的输入阻抗,则系统能稳定运行。本文主要研究PWM整流器输出阻抗特性对稳定性的影响。
文献[10]研究通过在直流母线处并联RC回路降低输出阻抗来提高系统稳定性。为减小文献[10]增加并联回路带来的损耗,文献[11,12]提出直流母线端并联调节器的方法,通过控制调节器调节直流母线上的纹波电流,改善系统稳定性。除此外,还可以通过改善系统的控制策略来改善系统的稳定性。文献[13]将直流母线电压中的交流分量经过补偿反馈回控制器,实现降低输出阻抗的效果,提高系统稳定性;文献[14]将直流母线电压的纹波小信号作为负反馈信号叠加到电压外环给定端,通过引入虚拟阻抗实现输出阻抗的优化,提高了系统稳定性。然而,通过改变控制的方法引入虚拟阻抗在提高系统稳定性的同时会导致电网侧电流谐波增加,电流畸变率变高[14,15]。
LCL滤波的PWM整流器与L滤波的PWM整流器相比,具有成本低、体积小、滤波效果好等优点[16]。目前文献多是针对L滤波的PWM整流器进行的,而对于网侧连接LCL型PWM整流器阻抗分析很少,本文首先对其建立小信号模型,研究其闭环输出阻抗特性,讨论分析了影响输出阻抗的相关因素;并针对所研究的充电系统中引入虚拟阻抗在提高系统稳定性时导致电网侧电流谐波增加的问题,本文提出一种变参数虚拟阻抗控制方法,既增强了直流侧系统的稳定性,又减小了网侧电流谐波,提高了网侧电流质量。仿真和实验结果验证了所提出方法的正确性。
2 LCL型PWM整流器建模与阻抗分析
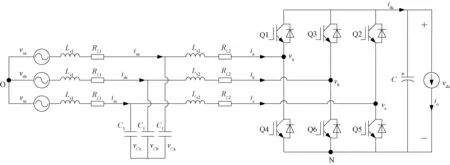
图1 LCL型PWM整流器拓扑图Fig.1 Topology diagram of PWM rectifier with LCL
2.1 PWM整流器模型
与网侧串联L型滤波器相比,LCL型滤波器能够降低总电感值、减小体积并能显著提高滤波效果[17]。如图1所示为三相LCL型PWM整流器拓扑图,根据基尔霍夫电压和电流定律建立dq坐标系下的三相PWM整流器的平均模型如下:
(1)
式中,Ls1为网侧电感;RL1为内阻;Ls2为整流器侧电感;RL2为内阻;C1为网侧LCL滤波电容;C为直流侧母线电容;ω为角频率;isd为dq变换后的网侧电流;id、iq为dq变换后的整流器侧电流;vCd、vCq为dq变换后的滤波电容端电压;vsd、vsq为dq变换后的网侧电压;vd、vq为dq变换后的桥臂中点电压;io为后级DC/DC充电系统用电流源;vdc为直流母线电压。
从式(1)可知,d轴与q轴电流变量之间存在相互耦合的影响,为了简化分析,对dq轴电流采取解耦控制的方法[18],且由于LCL型滤波器存在谐振尖峰,影响系统稳定性,通过采用网侧电感电流反馈的有源阻尼控制方法以抑制谐波振荡[19],令占空比满足如下关系:
(2)
式中,将占空比分为三部分,其中,gd1和gq1是控制系统输出的占空比大小,受电流内环调节器Gci的影响;gd2和gq2是生成耦合电流的占空比大小;gd3和gq3是采用网侧电感电流反馈增加有源阻尼的占空比,K为有源阻尼系数。考虑到滤波电容的数值极小,可以忽略ωvCd和ωvCq对式(1)中滤波电容模型的影响,同时根据式(2)的解耦方法对式(1)进行解耦分析,可得:
(3)
考虑到iq=0、vq=0,且dq电流互相解耦,vdc只与d轴分量有关。所以可以忽略q轴分量的影响,最终得到解耦降阶后的PWM整流器平均模型为:
(4)
设在直流工作点,d轴占空比为Gd1,d轴电流为Id,负载电流源为Io,直流侧电压为Vdc,考虑到当PWM整流器工作在稳态工作点时,有Isd、Id以及Vdc、VCd的变化量为0,可以得直流稳定工作点,如下所示:
(5)
对式(4)在稳态工作点附近做小信号扰动,忽略其中二次项,得到PWM整流器降阶后的小信号模型:
(6)
其所对应的输出方程为:
(7)
对式(6)、式(7)经过拉氏变换和矩阵运算可得(具体参数及符号见附录):
(8)
2.2 输出阻抗分析
根据输出阻抗定义,由式(8)可得三相PWM整流器的开环输出阻抗为:
(9)
根据式(9)采用电压外环与电流内环的控制结构得到降阶小信号模型闭环控制框图,如图2所示。其中,Gcv为电压外环PI控制器传递函数,Gci为电流内环PI控制器传递函数,其表达式如下:
(10)
式中,KP1为电压环比例系数;KI1为电压环积分系数;KP2为电流环比例系数;KI2为电流环积分系数。
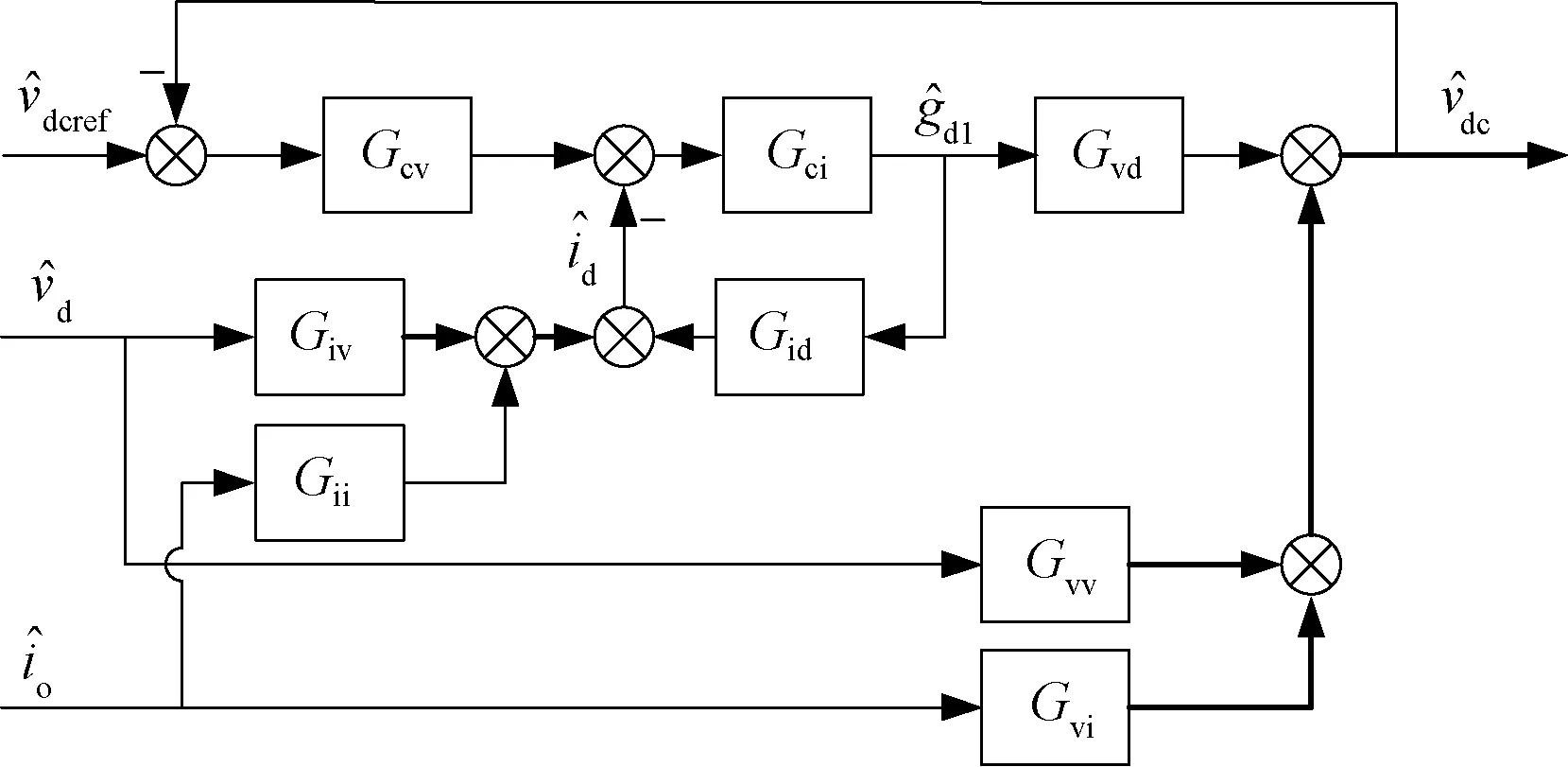
图2 PWM整流器小信号模型闭环控制框图Fig.2 Small signal model closed-loop control block diagram of PWM rectifier
由图2闭环控制框图,根据梅森增益公式可得闭环输出阻抗:
(11)
如图3所示为不同参数对输出阻抗影响。从图3(a)和图3(b)来看,直流母线电容容量主要影响输出阻抗的高频部分,电压环积分控制参数主要影响输出阻抗的低频部分,而对系统输出阻抗幅值最大值的中频部分基本没有影响;图3(c)说明改变电压环比例参数会改变系统输出阻抗的幅值最大值,影响系统的稳定性。而电压外环控制器参数由典型Ⅱ型控制系统的参数整定关系可以得出,其控制参数与直流母线电容正相关[20],所以在控制性能不受影响的情况下改变直流母线电容容量使其控制参数发生改变[21],系统稳定性将随着电容容量的减小而减弱,如图3(d)所示。所以,直流母线电容主要影响输出阻抗的高频部分,而电压环的比例参数对中频部分阻抗有一定影响,其积分参数主要影响低频部分,电流环控制参数对输出阻抗影响较小。
3 变参数控制
在不增加系统额外电路的情况下,将直流母线电压经过高通滤波器得到的纹波小信号作为反馈信号加到电压外环给定端[14],通过引入并联虚拟阻抗的方法实现输出阻抗的优化,提高系统稳定性,其控制框图如图4所示。
根据图4由梅森增益公式可得到引入母线电压小信号反馈的输出阻抗为:
(12)
式中,k为反馈系数。
由式(12)得到其输出阻抗伯德图如图5所示,其输出阻抗的极值随着系数k的增大而减小,反馈系数越大,输出阻抗的幅值就越小,系统稳定性越强,突加负载时直流母线电压波动幅度越小。但是,采用传统并联虚拟电阻的有源阻尼控制方式由于随着其反馈系数的增大,在稳定性增强的同时会引起稳态时网侧电流波形正弦度变差,谐波电流增大。为此,本文提出了一种基于变参数控制方法来解决母线电压小信号反馈系数过大导致的网侧谐波电流增加的问题。
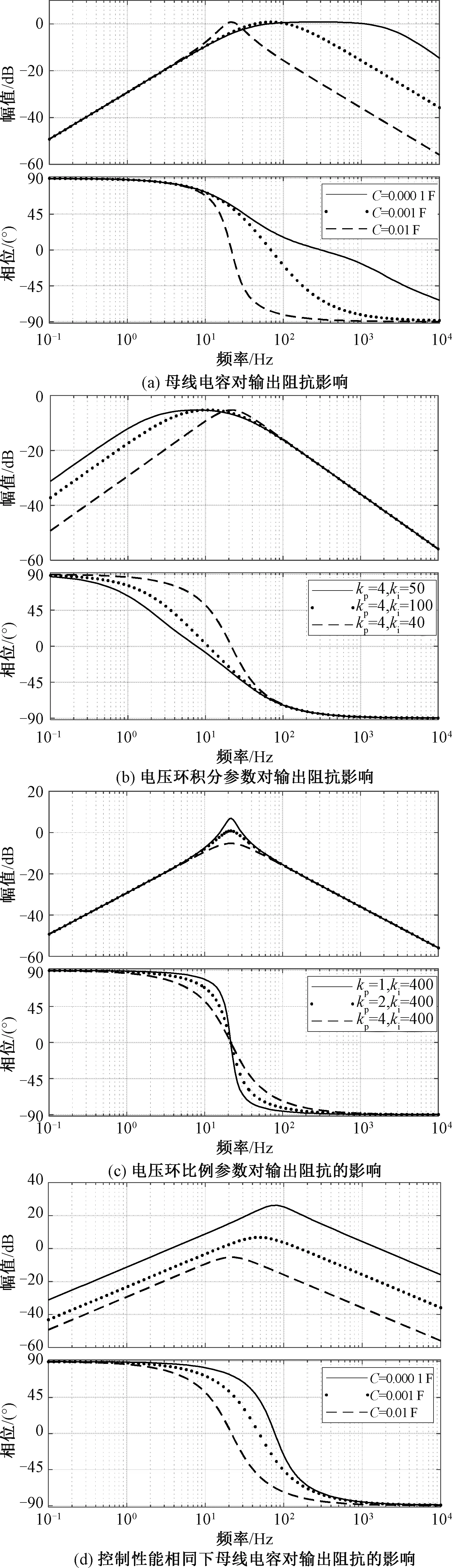
图3 影响输出阻抗的相关因素Fig.3 Factors affecting output impedance
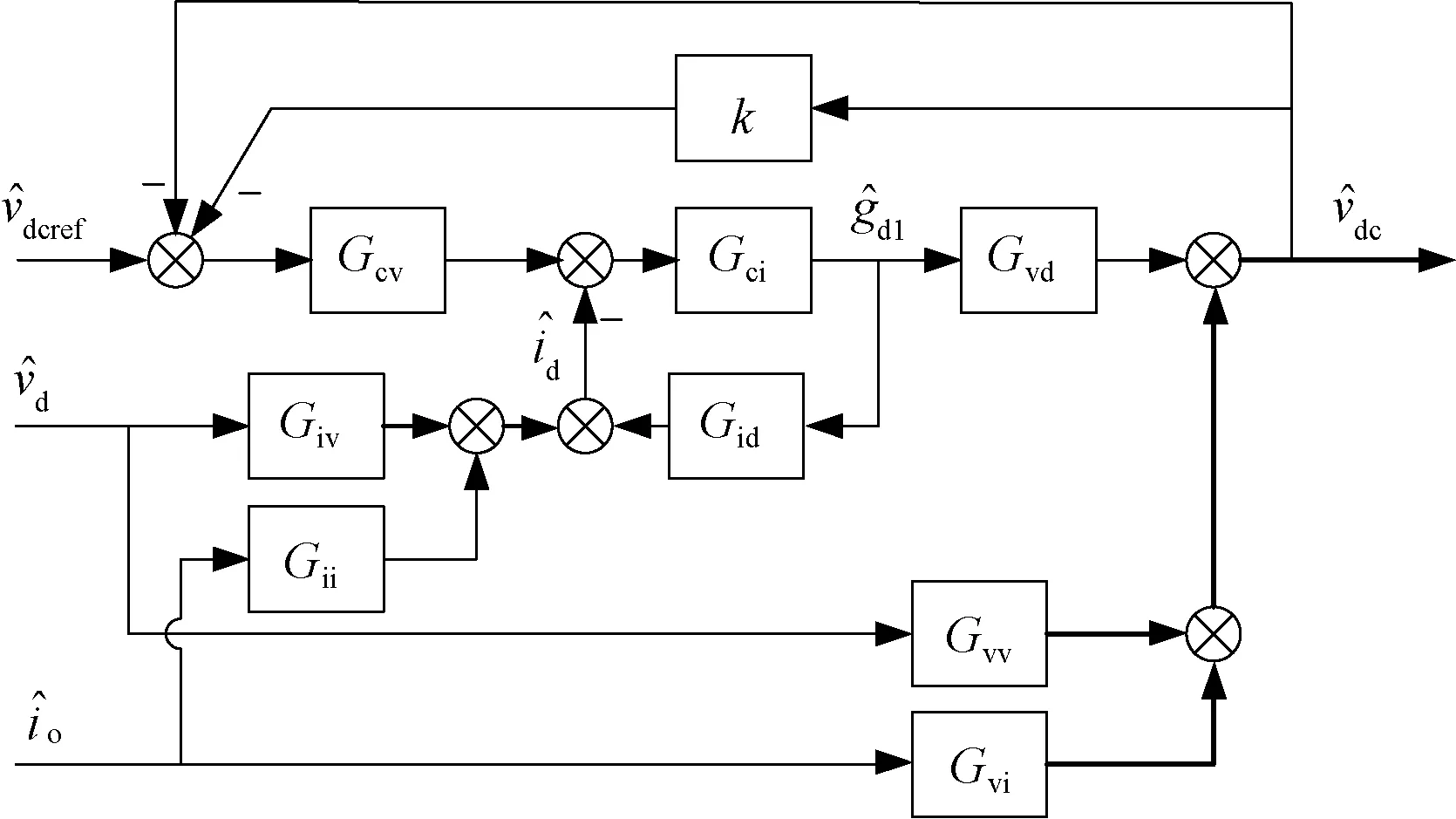
图4 母线电压小信号反馈的小信号模型闭环控制框图Fig.4 Small signal model closed-loop control block diagram of bus voltage small signal feedback

图5 母线电压小信号反馈Fig.5 Small signal feedback of bus voltage
传统控制器中的控制参数一旦确定就不能改变,也无法根据系统运行的实际情况对控制参数进行调整,因而存在控制效果不理想等情况。变参数控制策略是在不改变系统稳定性的情况下,根据系统的运行情况不断调整反馈系数k,使网侧电流谐波减少,正弦度得到改善。
其母线电压小信号反馈控制环节表达式为:
u=vdcGk
(13)
式中,k为反馈系数;G为高通滤波器,表达式如下:
(14)
式中,K0为增益(取K0=2);ω0为截止频率(ω0=2 000 rad/s)。
其变参数控制算法如下式[22]:
k=k0(1-αe-βerror2)
(15)
式中,error为被控量直流母线电压与母线电压给定值偏差值;k0为反馈系数初始值(取k0=6);α、β为修正系数(本文中α=1,β=-5)。
其基本思路是:反馈系数k随着偏差值error的大小变化。当偏差值较大时,引入反馈系数,使系统稳定性提高;当偏差值减小,减小反馈系数;当偏差值为零,即系统趋于稳定时,则撤去母线电压小信号反馈,使得稳态时的网侧电流波形得到改善。完整的PWM整流器控制框图如图6所示。
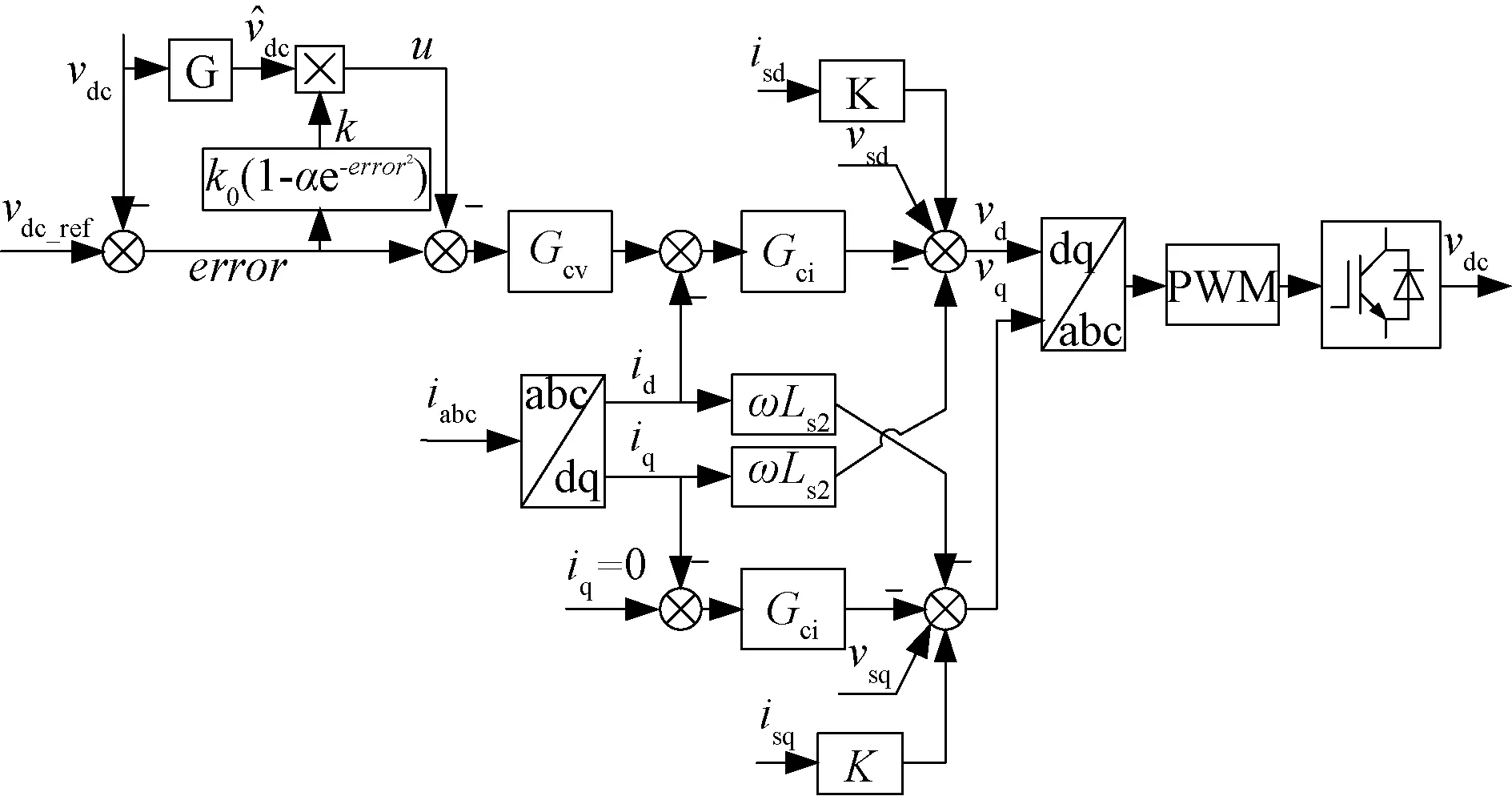
图6 PWM整流器控制系统框图Fig.6 Block diagram of PWM rectifier control system
4 仿真与实验结果分析
为验证上述的理论分析和变参数自适应控制的合理性与可行性,在Matlab/Simulink中搭建了如图1所示的三相LCL滤波的PWM整流器模型,对其进行仿真分析与验证。其中,网侧电压有效值为115 V,直流母线电压为300 V,整流器侧电感为1.5 mH,网侧电感为0.2 mH,滤波电容为10 μF、内阻为0.2 Ω,直流母线电容为0.001 F,开关频率为15 kHz,负载功率为525 W,电压环比例参数为0.5其积分参数为100,电流环比例参数为100其积分参数为100。
4.1 阻抗分析仿真验证
通过采用图7所示电流扰动注入的方法仿真测量三相LCL滤波的PWM整流器在不同频率的输出阻抗,如图8所示。图中实线为LCL型PWM整流器理论计算得到的阻抗Bode图,圆圈为LCL型PWM整流器在Simulink中仿真测量的阻抗Bode图,其理论结果与仿真结果的一致性,验证了理论分析计算结果的正确性与准确性。

图7 电流扰动注入法Fig.7 Current disturbance injection method

图8 三相PWM整流器闭环输出阻抗Fig.8 Three-phase PWM rectifier closed loop output impedance
4.2 系统输出阻抗优化与变参数仿真验证
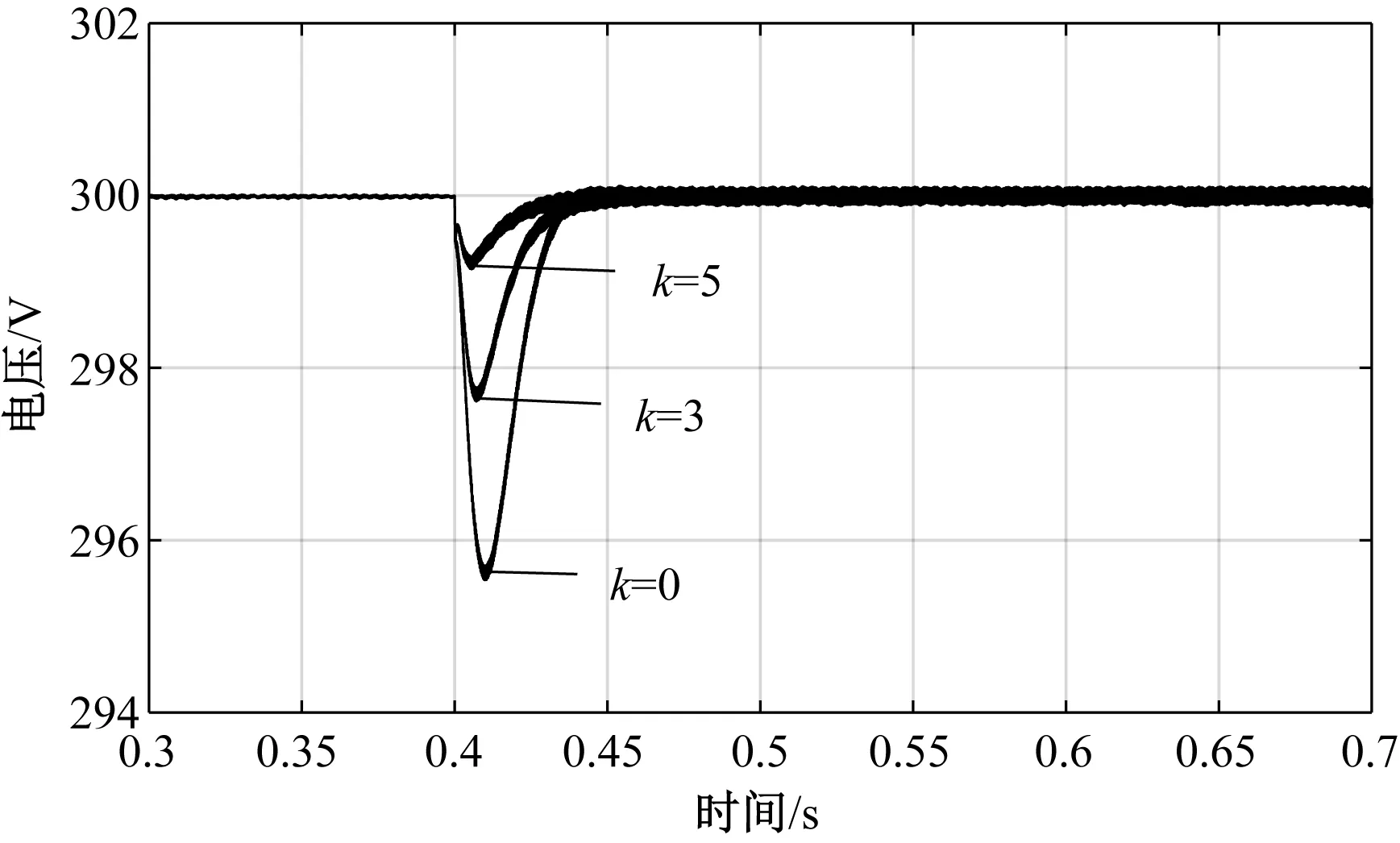
图9 不同反馈系数的直流母线电压波形Fig.9 DC bus voltage waveform with different feedback coefficients when load is applied
仿真或实验环境下通过观察负载变化时直流母线电压波动大小直观观测级联系统运行稳定性情况[14,15,21]。当PWM整流器运行稳定后,在0.4 s突加负载,得到如图9所示参数不变情况下不同反馈系数的母线电压波形图,图10为不引入母线电压小信号反馈稳态时的网侧电流波形图和其谐波分析图,图11和图12分别为反馈系数为3和6时的稳态响应。从图9中可以看出,随着反馈系数的增加,其母线电压波动减小,级联系统稳定性得到了改善。但从图10~图12可知随着反馈深度的增加,稳态时的网侧电流谐波增加。图10(b)中利用FFT工具分析在不引入母线电压小信号反馈环节稳态时的网侧电流的THD=3.16%;图11(b)为当k=3时得网侧电流波形图,其谐波增加较多,此时的THD=4.48%;图12(b)为当k=6时得网侧电流波形图,其谐波有所增加,此时的THD=5.13%。
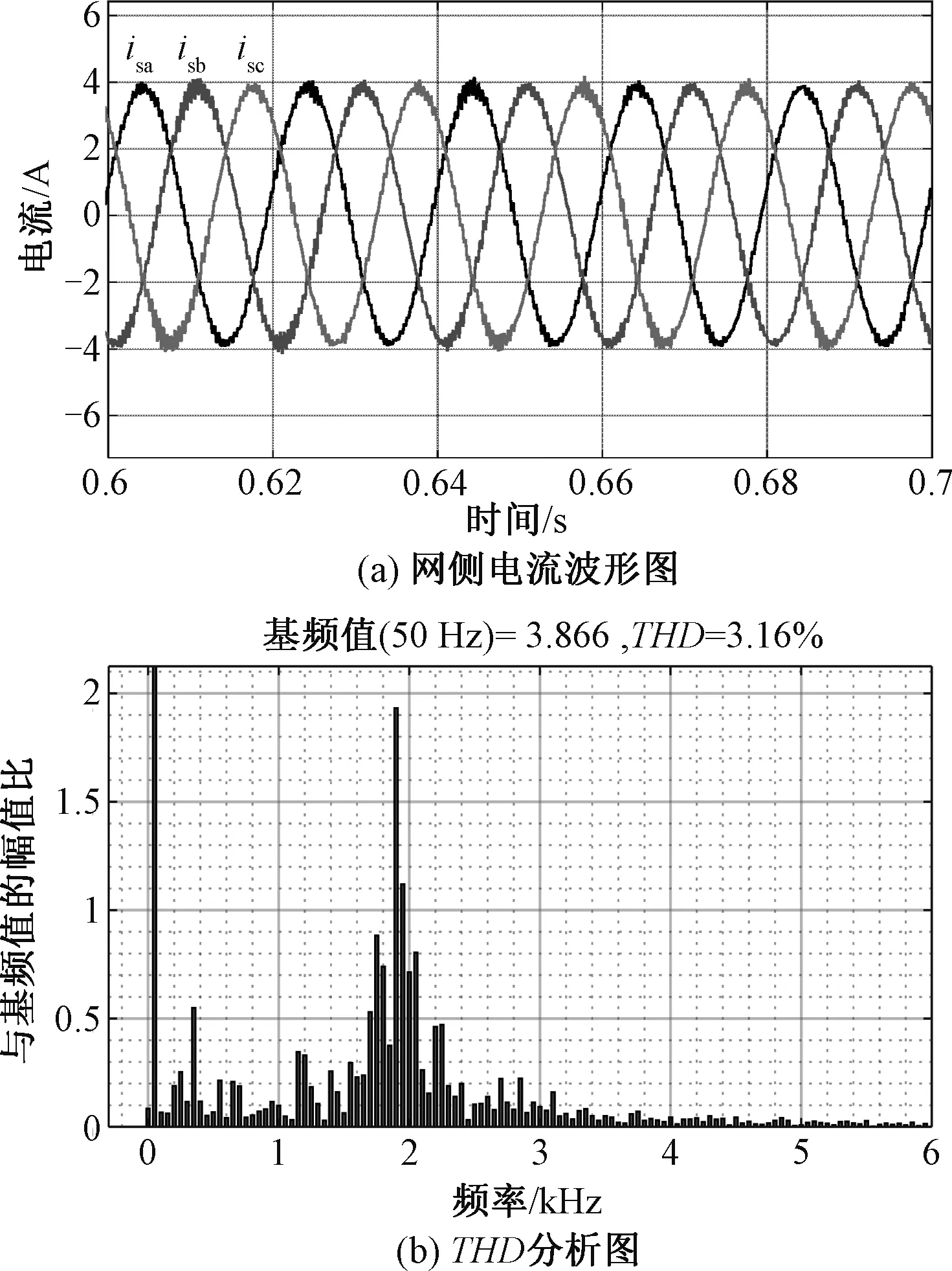
图10 不引入母线电压小信号反馈时的稳态响应Fig.10 Steady-state response when small signal feedback of bus voltage is not introduced

图11 反馈系数k=3时的稳态响应Fig.11 Steady-state response when k=3

图12 反馈系数k=6时的稳态响应Fig.12 Steady-state response when k=6
图13为引入变参数控制后的母线电压波形图。从图中可以看出采用变参数控制后,直流侧电压波动大小几乎不变,级联系统稳定性基本不受影响。图14为k=6时采用变参数控制其网侧电流波形图,与图12不采用变参数控制相比,其稳态时的网侧电流波形正弦度较高,其THD=3.76%,网侧电流谐波得到有效降低。说明采用变参数控制在提高级联系统稳定性的前提下其网侧电流波形得到了有效改善。

图13 采用变参数控制的直流母线电压波形Fig.13 DC bus voltage waveform adopting variable parameter control
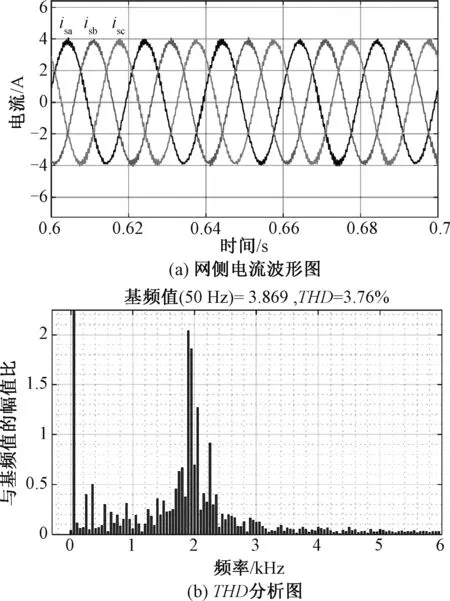
图14 采用变参数控制网侧电流波形和谐波分析图(k=6)Fig.14 Variable parameter control grid-side current waveform and harmonic analysis diagram (k=6)
4.3 实验验证
为进一步验证阻抗优化方法及变参数控制对提高系统稳定性和改善网侧电流波形的有效性,搭建了基于TMS320F28335的三相LCL滤波器的PWM整流器的实验平台,后级通过DC/DC变换器与电池相连。电池为四块铅酸电池串联,单块电池电压12 V,实测总内阻为0.2 Ω,容量为100 A·h。当整流器稳定工作后,分别在不引入反馈、引入母线电压小信号反馈及采用变参数算法下对电池施加10 A电流充电,得到如图15~图17所示的响应波形。
图15为不引入反馈系数时加载实验波形,从图中可看出其母线电压跌落了11 V,从图15(b)和图15(c)得知,加载时刻与稳态时的网侧电压与网侧电流同相位且正弦度较好,整流状态工作正常,稳态时的网侧电流THD=3.75%。图16为引入母线电压小信号反馈后的实验波形图,此时的反馈系数k=3,与不引入反馈相比其母线电压跌落了3 V,振幅较小,级联稳定性得到了有效改善。但是与图15(c)对比可知,引入母线电压小信号反馈后,其网侧电流的波形正弦度变差,其THD=5.47%,说明引入母线电压反馈后,导致网侧电流谐波增加。

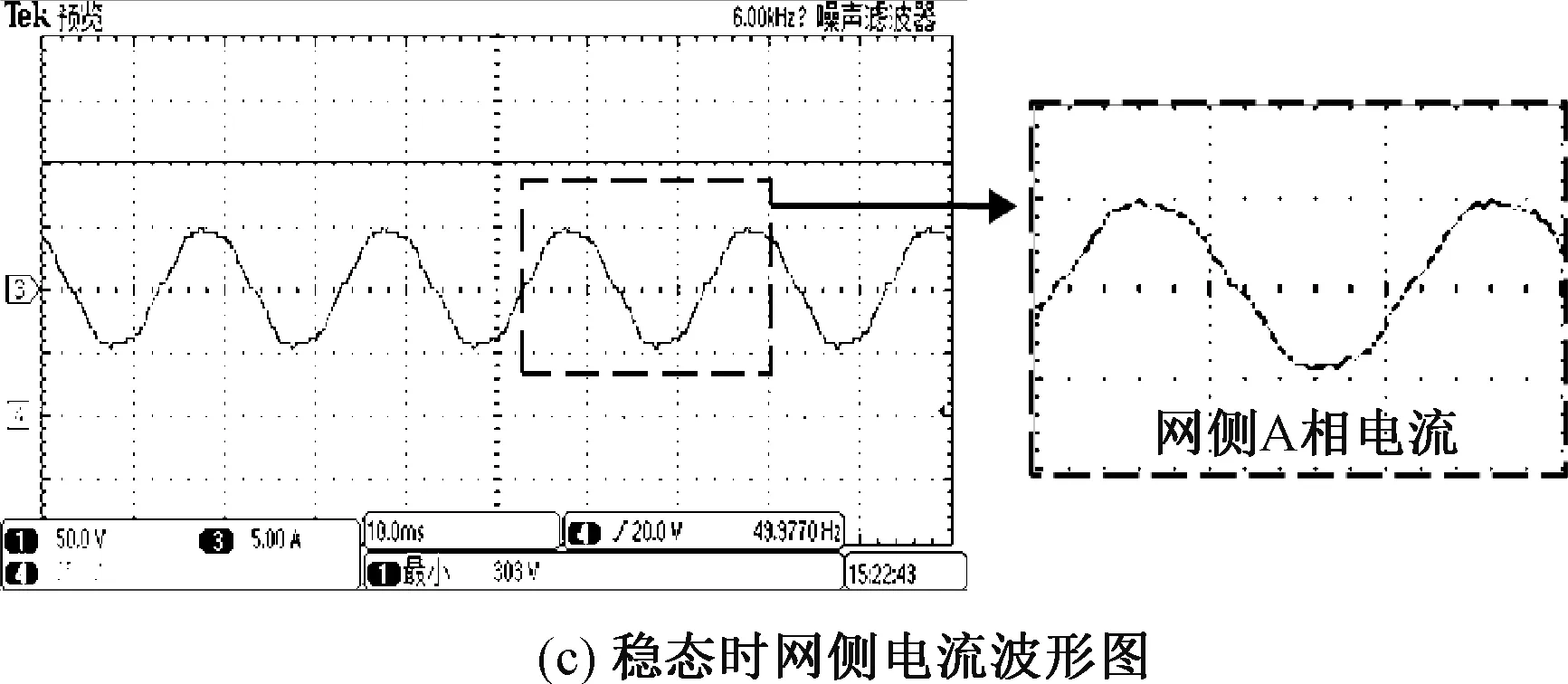
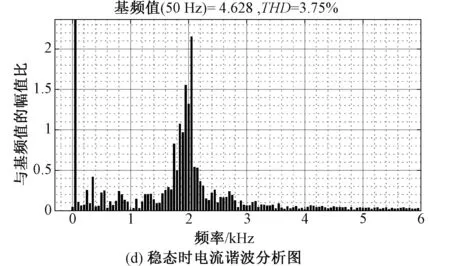
图15 不引入反馈时的响应波形Fig.15 Response waveform without feedback

图16 引入母线电压小信号反馈时的响应波形Fig.16 Response waveform when small signal feedback of bus voltage is introduced
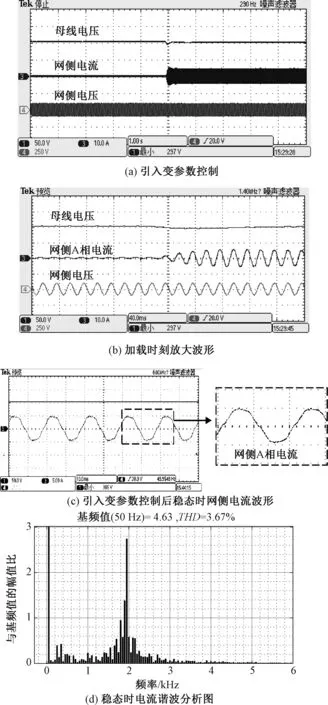
图17 引入变参数控制的响应波形Fig.17 Response waveform when introducing variable parameter control
图17所示为在母线电压小信号反馈的基础上通过引入变参数控制后的相应波形图,其母线电压小信号反馈系k=3。与图16引入母线电压小信号反馈的实验波形对比可知,加载后母线电压幅值同样只跌落了3 V,且其网侧电流的THD=3.67%,对比图16(c)可以发现引入变参数控制后,在不改变级联系统稳定性的前提下,有效改善了网侧电流波形质量,验证了该方法的有效性。
5 结论
在大功率电动汽车充电系统中,PWM整流器的输出阻抗是影响后级DC/DC变换器电池充电装置稳定运行的重要因素之一。论文对网侧LCL滤波器的PWM整流器进行了小信号建模,研究了影响其输出阻抗的相关因素,并通过仿真验证了理论分析的正确性与可行性。仿真和实验证明在基于直流母线电压小信号反馈控制方法中引入变参数自适应控制既能降低输出阻抗提高级联系统稳定性,又能有效减小稳态时的网侧电流畸变,改善网侧电流质量。论文研究为大功率电动汽车充电系统中LCL滤波器的PWM整流器与DC/DC电池充电装置设计提供参考。
附录
LCL型PWM整流器降阶后的小信号模型为:
(A1)
该降解模型所对应的输出方程为:
(A2)
对式(A1)、式(A2)进行拉氏变换,可得:
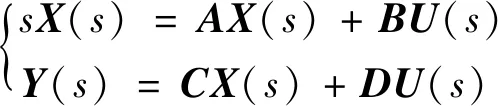
(A3)
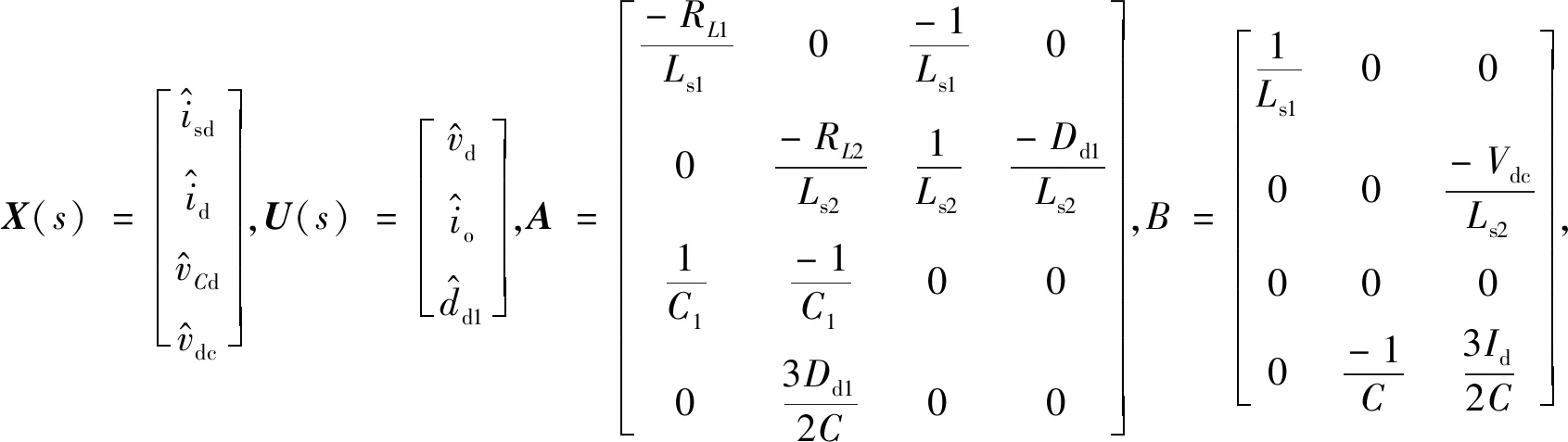

由式(A3)进行矩阵运算可以得到:
(A4)
根据式(A4)可以得到:
(A5)
式中
(A6)
