基于谐波磁链偏差的多模式调制切换策略研究

周 亮，苏和鹏，韩金洋

(1.海军工程大学舰船综合电力技术国防科技重点实验室，湖北 武汉 430033；2.92730部队82分队，海南 三亚 572016)

1 引言

在大功率电力牵引驱动系统中，为降低开关损耗，提高输出功率，逆变器需要工作在几百赫兹以内的低开关频率。为改善低开关频率下驱动电机的谐波畸变，逆变器通常采用同步优化脉宽调制(Pulse Width Modulation，PWM)[1-3]。电力牵引系统的基本要求是满足列车较宽的运行范围，为了保证牵引电机在全速度范围内的平稳运行，除了常规异步调制[4，5]外，还需要引入优化PWM的多模式分段调制策略[6-9]。

不同调制模式之间的过渡阶段，调制方式的切换难以保证状态连续，容易引起电流振荡，造成系统不稳定。因此不同模式之间的平滑切换是工程应用中需要解决的实际问题。目前应用较多的切换策略主要有两种：一是基于工程考虑分析选择冲击最小的切换点进行切换；二是基于定子磁链偏差消除的控制切换策略。

基于工程考虑，文献[10]通过推导谐波电流与电压基波相位之间的关系，总结得到对过渡过程影响最小的切换时刻，但并未揭示机理。文献[11]基于基波连续的原则对中间60°调制的切换策略进行研究，但无法选择最优切换点。确定切换点后，切换动作在三相同时进行，可以充分简化牵引电机的切换算法，但切换时三相之间存在耦合，切换原则缺乏理论依据[12]。分析电流冲击的产生原理，可以对切换控制策略提供理论依据。文献[13]从电路原理的角度，解释了电流和转矩在暂态响应过程中发生冲击的机理，并证明了三相独立切换算法的合理性，但对于切换条件的判断没有形成一个通用简单的方法。

定子磁链轨迹控制策略通过修正开关角补偿切换过程的调制误差，可以明显降低切换过程的转矩冲击，但没有考虑切换前后的调制规律[14]。文献[15,16]则借鉴直接自控制(Direct Servo Control,DSC)思想，提出改进的定子磁链轨迹跟踪方法跟踪理论磁链阈值，解决切换冲击问题，实现了分段调制模式下的平滑运行。通过分析定子磁链轨迹的变化规律，基于电机定子磁链分析的电流谐波最小PWM(Current Harmonic Minimum PWM,CHMPWM)切换策略被证明是可行的[17-19]。文献[17]介绍了一种利用定子磁链轨迹重合点确定切换点的方法，但磁链轨迹无法全面表示矢量之间关系。文献[18]提出了基于定子磁链幅值偏差和谐波磁链幅值的切换策略，只需要对优化开关角进行推导就可以选择最优的切换时刻，但结合两个幅值量确定切换点需要分情况进行具体选择，分析过程较为复杂。

本文基于谐波磁链分析的方法，提出一种通过计算谐波磁链偏差幅值确定最佳切换点的策略。该方法对优化开关角进行推导计算得到谐波磁链偏差幅值，根据幅值大小即可对切换时刻进行选择，不需要复杂的理论计算。通过仿真和半实物实验验证了切换策略的有效性。

2 多模式调制切换冲击问题

2.1 多模式分段调制

受到高压大功率开关器件本身特性、开关损耗以及散热的限制，牵引逆变器的最高开关频率一般在几百赫兹以内。在低开关频率下，使用异步PWM调制时，会导致电机在高速区产生较大的电流谐波畸变和转矩脉动，甚至无法正常运行。要想减小谐波，应采用同步且对称的优化PWM调制，如CHMPWM调制，使开关频率随着输出频率同步变化，使输出波形保持正负半周对称、半周期中左右对称。

多模式分段调制策略将整个逆变器输出频率范围分成若干频段，如图1所示。每一个频段都可以根据不同工况采用不同方式。一般情况下，低频阶段采用异步PWM以充分利用开关频率，高频采用不同载波比(fs/f=N1,N2,N3,…,1)的同步优化PWM以利用很少的开关次数获得最佳的谐波性能。

图1 多模式分段调制策略Fig.1 Multi-mode modulation strategy

2.2 切换冲击产生原因

异步调制切换到同步调制时一般不会引起冲击，而不同载波比的同步优化PWM进行切换时，将会产生较大的电流冲击。其原因主要有两个：一个是原有谐波电压的幅值和相位突变引起的冲击；另一个是引入了新的谐波成分导致的冲击。

图2(a)为感应电机谐波等效电路，n为谐波次数，sn为n次谐波的转差率。通常，电机励磁支路阻抗远远大于谐波漏抗，因此可以去掉励磁支路，若进一步忽略电机定、转子电阻对电压的影响，从而可将电机谐波等效电路简化为图2(b)的近似电路。

图2 感应电机谐波等效电路Fig.2 Harmonic equivalent circuit of induction motor

由切换过程的谐波等效电路可知，切换过程可以等效为各次谐波的暂态响应过程，表示为原有谐波含量突加一个冲击分量，则切换后的n次谐波电压可表示为：

un+=Umn-sin(nωt+φn)+ΔUmnsin(nωt+φn)

(1)

式中，Umn-为切换前的n次谐波电压幅值；ΔUmn为n次谐波电压的暂态冲击分量幅值；φn为n次谐波电压切换时的相位。

将切换冲击电流看作电压冲击的零状态响应，对于图2(b)简化后的电路而言，可得到n次谐波的冲击电流为：

(2)

式中，L1s和L1r分别为定、转子漏感；ωe为同步角速度；τ为时间常数；φ为阻抗角，φ≈π/2。

对于选择性谐波消除PWM(Selective Harmonic Eliminated PWM,SHEPWM)调制来说，若在基波电压峰值处切换，此时φn=nπ/2，且n为奇数，由式(2)可知sin(φn-φ)≈0，可以消除电流冲击。但对于CHMPWM来说，分析其谐波特性以确定切换相位的方法则对计算量提出了更高的要求。

除了电压电流谐波之外，也可以利用定子磁链矢量来判断PWM的性能和变化趋势。当忽略定子电阻时，谐波电流、谐波电压和谐波磁链之间存在以下关系：

(3)

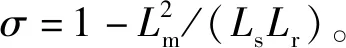
则切换前后谐波电压的变化会反映到谐波磁链的变化为：

(4)

式中，ψh1和uh1分别为切换前的谐波磁链和电压；ψh2和uh2分别为切换后的谐波磁链和电压。切换前后的谐波电压uh不同导致切换冲击，也可以将切换冲击产生的原因归结为不为0的谐波磁链偏差Δψh。

如图3所示，谐波磁链的产生是优化PWM电压产生的电压磁链(V1T1-V2T2)与参考磁链路径ψs_ref不同所导致的。

图3 谐波磁链的产生原理Fig.3 Cause of harmonic flux linkage

3 基于谐波磁链偏差的切换策略

3.1 平滑切换原则

对于感应电机而言，电磁转矩可以表示为：

Te=Km|ψr||ψs|sinγ

(5)

式中，Km为常数；ψs和ψr分别为定子磁链和转子磁链；γ为定子磁链矢量和转子磁链矢量之间的夹角。

转子磁链幅值给定为常值，则电磁转矩主要由定子磁链矢量决定。若能对定子磁链矢量的幅值和相位进行控制，则能对电机的电磁转矩进行控制。在模式切换过程中，定子磁链轨迹的切换是造成电流和转矩冲击的根本原因。若要实现平滑切换，需定子磁链轨迹连续平滑变化，即保证切换前后定子磁链的幅值和相位是连续的。当保证定子磁链轨迹平滑过渡，相应地就能保证电磁转矩和电流的平稳过渡。

基于上述原则，定子磁链轨迹控制算法可以控制切换后的定子磁链矢量跟踪切换前的定子磁链矢量以实现磁链轨迹连续。但因为脉冲修正算法是滞后于变化时刻的，且磁链修正的幅度有限，若直接将定子磁链轨迹控制算法应用于调制模式之间的切换过程，并不能充分保证修正效果。为充分消除切换冲击，可以对切换点进行预先选择。若能选择切换点的磁链偏差很小，则此时切换前后的定子磁链相对连续，相应地能保证调制模式的平滑切换。

3.2 定子谐波磁链

当三相电机连接到逆变器时，定子电压等于逆变器电压，忽略定子电阻，t时刻的定子磁链矢量ψs=[ψsαψsβ]T为：

(6)

式中，ψs(0)为积分初始值；m为调制比；Us(ωst)=[UsαUsβ]T；ωs为定子角频率。

又由于定子电压矢量相位角θ=ωst，可将定子磁链表达式变换为关于角度θ的函数：

(7)

进一步整理得：

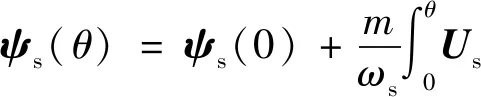
(8)

式中，积分变量ϑ∈[0,θ]；积分初始值ψs(0)应使磁链轨迹以原点为中心，因此积分初始值为定子磁链整个基波周期内积分的平均值，表示为：

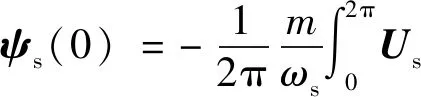
(9)

为了定量计算磁链偏差的大小，定义谐波磁链矢量等于实际定子磁链与参考定子磁链矢量之差，则可得谐波磁链矢量的表达式为：

ψhN=ψN-ψref=(ψNα-ψrefα)+j(ψNβ-ψrefβ)

(10)

式中，ψhN为谐波磁链矢量；ψN为优化脉冲模式下定子实际磁链矢量；N为1/4基波周期内开关角数量；ψref为参考定子磁链矢量，轨迹为标准圆。

以N=3，m=0.8为例，在一个基波周期内对式(10)进行积分计算，画出谐波磁链矢量ψh3示意图和谐波磁链轨迹图，如图4所示。

图4 N=3,m=0.8时谐波磁链Fig.4 Harmonic flux trajectory when N=3,m=0.8

从图4(b)可以发现，谐波磁链轨迹同样存在周期对称性，如果实际磁链矢量与参考磁链矢量的相位和幅值连续，则理论上谐波磁链应为零。但是由谐波磁链轨迹无法准确判断过零点时刻，因此对谐波磁链的幅值进行计算：

(11)

图5为定子磁链轨迹和谐波磁链幅值波形。从图5(a)可看出在θ=0～60°范围内实际磁链轨迹与参考磁链轨迹存在不止一个重合点，而图5(b)中谐波磁链幅值仅在θ=30°时才接近零，二者似乎存在矛盾。但从图5(c)可以清晰地看出，尽管实际磁链与参考磁链的幅值之差有多处等于零，但同时它们的相位之差也等于零的时刻仅在θ=30°处。这种现象可解释为：图5(a)中实际磁链矢量的旋转速度并不是匀速的，而参考磁链矢量是匀速旋转的，轨迹图中二者的重合点在时间上并不一定是同一时刻，这也证明了利用定子磁链轨迹的重合点来选择切换时刻的局限性。而利用谐波磁链偏差来进行不同模式之间的切换点选择，可以保证切换前后的谐波磁链连续，实现平滑过渡。

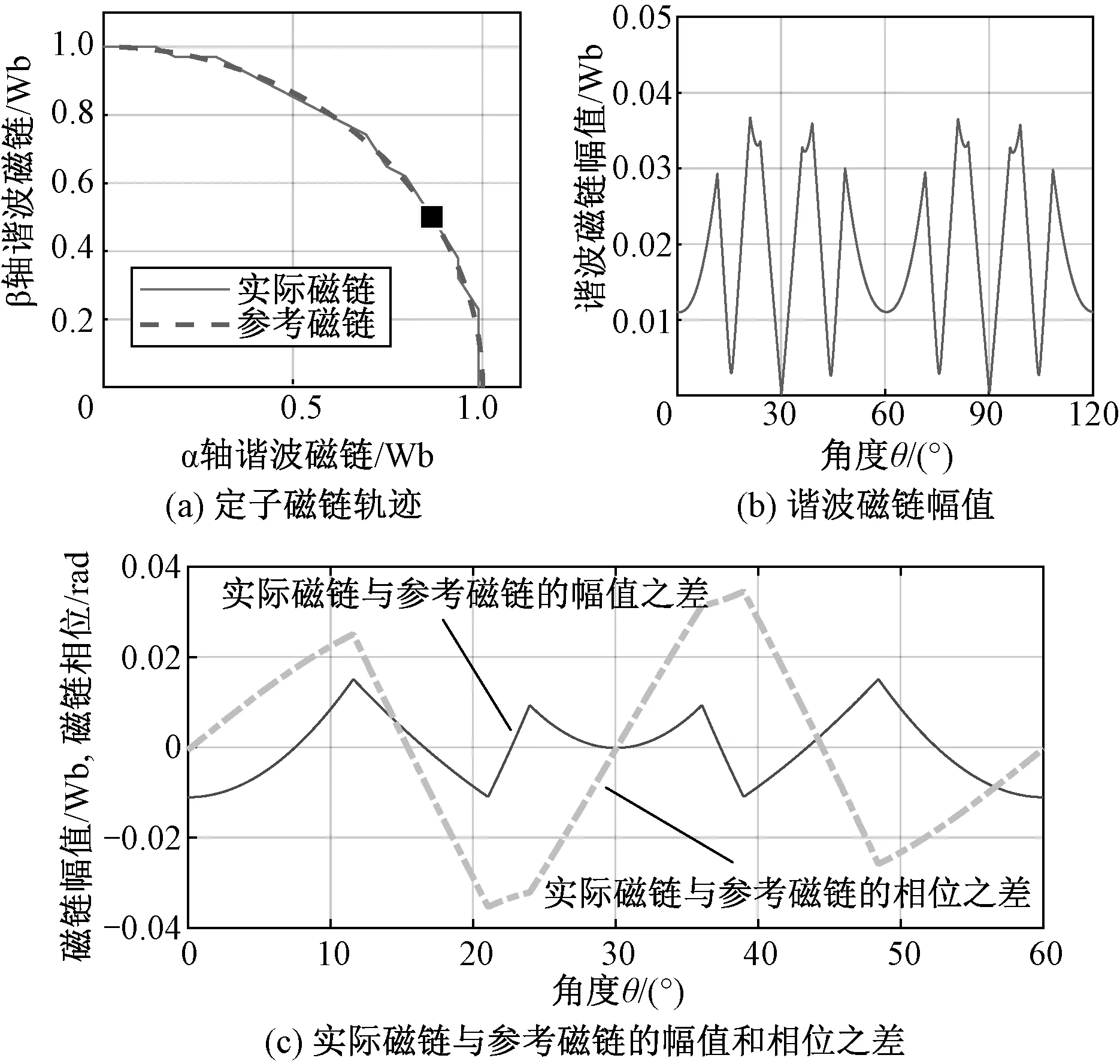
图5 定子磁链轨迹和谐波磁链幅值波形(N=3,m=0.8)Fig.5 Stator flux trajectory and amplitude of harmonic flux

3.3 最佳切换点

根据优化PWM脉冲模式对称性，αβ坐标系下的定子磁链轨迹可划分为六个扇区，六个扇区具有周期性，以下对0～60°扇区进行分析。图6为N=5和N=3模式下的稳态定子磁链轨迹。

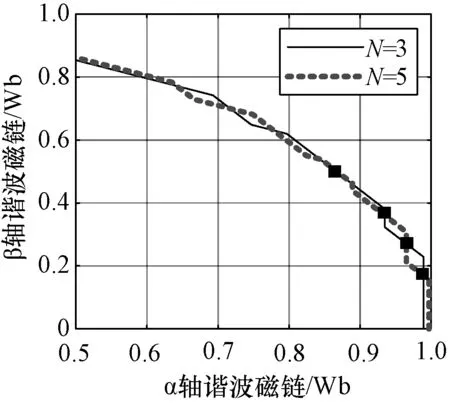
图6 N=3和N=5时定子磁链轨迹Fig.6 Stator flux trajectory when N=3 and N=5

图6中，标注点为二者的重合点，由3.2节的分析可知，轨迹重合点不能作为切换点的选择依据。而磁链矢量包含幅值和相位信息，可以作为切换点的选择依据。

图7展示了切换前后N=5和N=3的定子磁链矢量和谐波磁链矢量之间的关系。若要保证切换前后定子磁链矢量的幅值和相位连续，可以等效为切换前后的谐波磁链矢量连续，即ψh3=ψh5。对应上述情况，若切换前后的谐波磁链偏差等于0时，则切换前后的谐波磁链矢量是连续的。而谐波磁链偏差越小，代表切换前后磁链矢量的幅值和相位越接近，谐波磁链偏差的幅值可以体现切换前后谐波磁链的关系。当谐波磁链偏差的幅值等于0时，ψh3和ψh5必然重合。类似的，谐波磁链偏差的幅值越小，证明切换前后谐波磁链之间的距离越小。

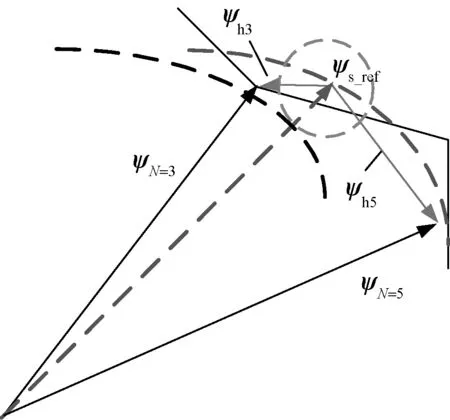
图7 切换前后定子磁链和谐波磁链矢量之间的关系Fig.7 Relationship between stator flux and harmonic flux before and after switching

以N=5和N=3两种模式为例，为了进一步分析谐波磁链偏差的幅值分布情况，以确定切换时刻，定义切换前后的谐波磁链偏差的幅值|Δψh|为：

|Δψh|=|ψh3-ψh5|

(12)

根据上文分析可知，当切换前后的谐波磁链偏差为0时，可以保证切换前后的谐波磁链连续。对谐波磁链偏差进行定量计算，可以得到N=5和N=3模式切换时谐波磁链偏差的幅值|Δψh|关于角度θ的分布，如图8所示。

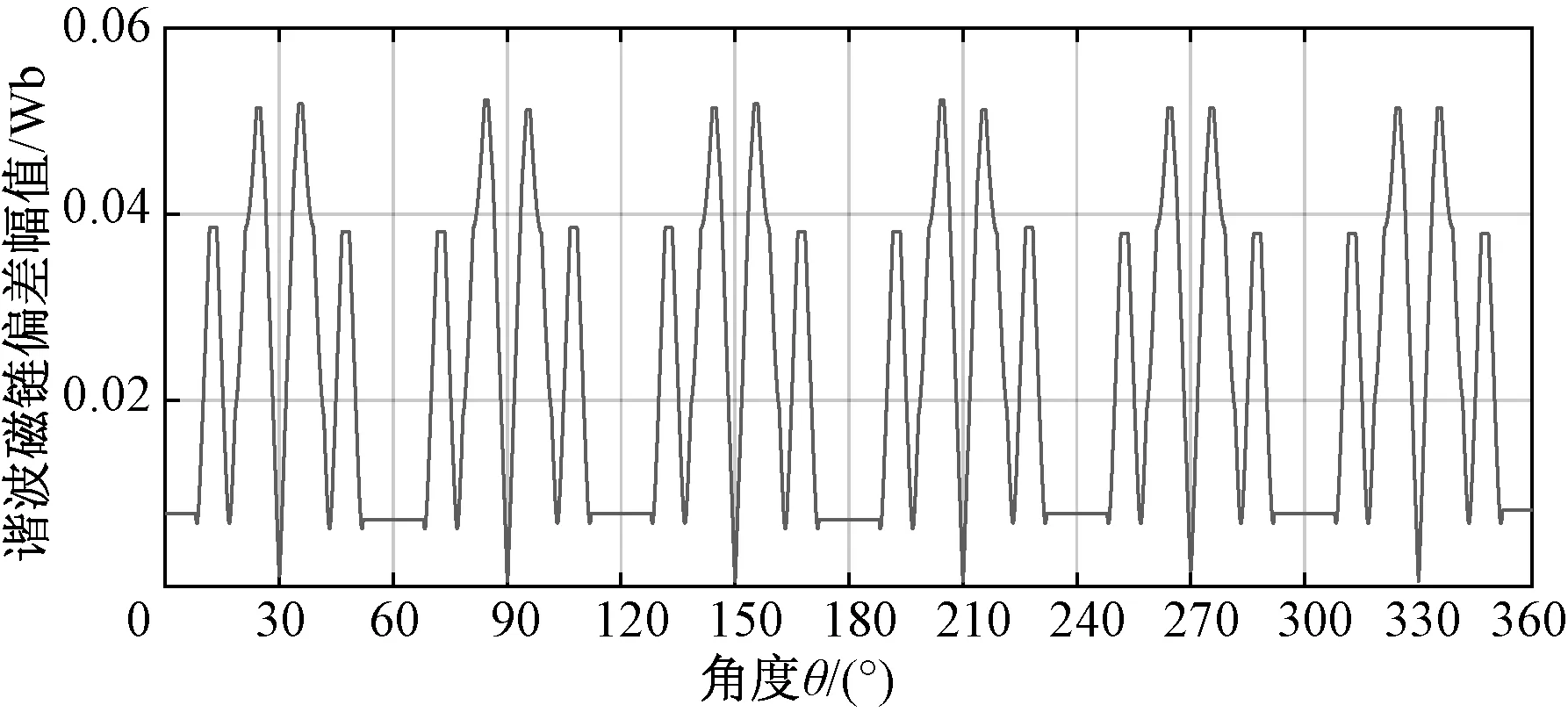
图8 谐波磁链偏差的幅值Fig.8 Amplitude of harmonic flux error

从图8中可看出，谐波磁链偏差的幅值同样存在周期性，在θ=0～60°扇区范围内，谐波磁链偏差的幅值在θ=30°处最小，|Δψh|≈0，此时切换电流和转矩冲击最小；在θ=24°和θ=36°附近谐波磁链偏差的幅值达到最大，|Δψh|≈0.052 Wb，此时切换冲击将达到最大值，效果最差。其他扇区具有相似的结论，因此整个基波周期内所有最佳切换点相位为{30°，90°，150°，210°，270°，330°}。

对于其他优化PWM，只需得到对应调制比的优化开关角即可重构定子磁链矢量，并得到谐波磁链矢量的分布，再根据谐波磁链偏差的幅值对最佳切换点进行选择。当偏差幅值存在0点时，则选择0点，若全范围内不存在0点，则选择幅值最小的时刻。由于谐波磁链偏差的幅值具有周期性，因此在基波周期内最佳切换点不止一个，如上文分析的N=5和N=3模式最佳切换点有6个，为了尽快完成切换，可按照就近选择的原则，选择离当前相位最近的最佳点切换。

此外，该方法分析的是定子磁链综合矢量，选择的时刻是三相整体冲击最小处，属于三相同时切换算法。因此该方法具有通用性，且分析过程进一步简化，只对谐波磁链矢量偏差的幅值进行判断，不需要逐一情形进行分析。

4 仿真与实验验证

为验证理论分析正确性，基于MATLAB/Simulink仿真软件对切换策略进行仿真，并搭建了RT-Lab半实物实验平台进行验证。牵引逆变器采用三电平中点钳位式(Neutral Point Clamped，NPC)电路拓扑，如图9所示，采用图1所示的多模式分段调制策略控制感应电机，在切换频率处设置了±0.5 Hz的滞环，当同时满足频率切换点和相位选择点的时候进行切换。

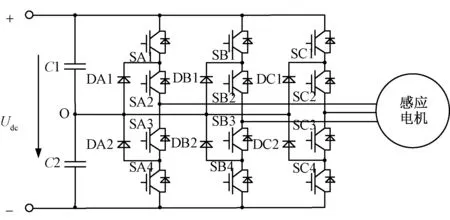
图9 三电平NPC逆变器驱动系统Fig.9 NPC three-level inverter driving system

牵引感应电机的具体参数见表1，电机采用基于间接转子磁场定向的控制策略。实验设定转速指令为3 400 r/min，电机经历异步调制→N=7→N=5→N=3→N=1同步调制模式的调速过程。

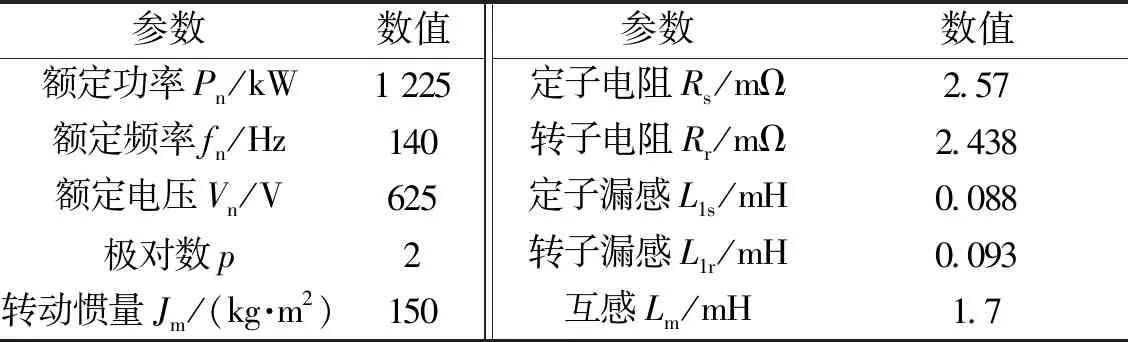
表1 感应电机参数Tab.1 Induction motor parameters

4.1 仿真结果

为了对比不同相位下切换对系统冲击的影响，本文选取N=5到N=3切换的仿真结果进行说明，仿真波形如图10所示。

图10 不同相位下切换过程波形Fig.10 Switching waves under different phases

仿真中，N=5到N=3之间的频率切换点为42 Hz，并分别在相位θ=10°、24°和30°处进行调制模式切换。从图10仿真波形可看出，在θ=24°切换时，由于切换前后谐波磁链偏差的幅值将达到最大值，此时的定子电流和电磁转矩冲击也最大，冲击电流为510 A，而电磁转矩波动达到了1 360 N·m，定子磁链幅值波动也有0.1 Wb；而在θ=30°切换时，定子电流、电磁转矩和定子磁链幅值均没有明显冲击或波动，冲击电流仅为67 A，转矩波动减小到80 N·m，定子磁链幅值波动近似为零，与理论分析的最佳切换点效果完全一致；在θ=10°切换时，电流冲击、转矩和定子磁链幅值波动大小介于24°和30°切换之间，仿真结果验证了理论分析的正确性。

4.2 实验结果

为了进一步验证切换策略的有效性，进行了半实物实验验证，实验平台如图11所示。

图11 实验平台Fig.11 Experimental platform

实验中，实时仿真目标机是感应电机和三电平逆变器实时模型的运行平台。实验时将设计的驱动系统模型经MainControl软件进行编译，并上传到实时仿真目标机。控制器是基于DSP 28335+FPGA Virtex-4完成软件编程，再利用仿真主机完成试验的操作运行。实验电机模型参数与仿真相同。

本文采用优化CHMPWM调制方法，IGBT开关输出脉冲波形如图13所示。图12中，S1、S2、S3、S4分别代表单个桥臂上的4个IGBT的开关信号，基波频率设置为100 Hz，调制模式N=3。根据NPC逆变器的工作原理可以推导出输出相电压波形，可以发现脉冲满足1/4周期对称和半波奇对称性。

图12 优化PWM输出脉冲波形(N=3)Fig.12 Waveform of optimal PWM output pulse (N=3)

图13为优化CHMPWM不同调制模式下进行切换的实验结果。电机进行异步调制→N=7→N=5→N=3→N=1的频率切换点分别为42 Hz、57 Hz、85 Hz、110 Hz，并根据本文提出的最佳切换点选取方法选择切换相位。从图13所示的实验波形可看出，切换过程实现了电压电流的平滑过渡，并未出现任何冲击。

仿真和实验过程都实现了不同调制模式之间的无冲击切换，证明了基于谐波磁链偏差的多模式调制切换策略是有效的。同时，这种分析方法也适用于其他优化PWM，只需要得到优化PWM的开关角，即可根据脉冲序列重构稳态定子磁链，对切换前后的谐波磁链偏差进行定量分析，便可根据幅值大小选择最佳切换相位，实现平滑切换。

图13 切换过程实验波形Fig.13 Experimental waveforms of switching process

5 结论

本文对基于优化PWM的多模式调制切换策略进行了研究，得到以下结论：

1)产生切换冲击的直接原因是不同调制模式切换前后的谐波特性突变，可以归结为谐波磁链的突变。要避免切换过程电流和转矩冲击的产生，需要保证切换前后的谐波磁链是连续的。

2)切换前后的定子磁链矢量可以从优化脉冲模式推导得到，基于谐波磁链偏差幅值的分析可以选择不同优化PWM模式之间的最佳切换点。该方法分析对象为定子磁链矢量，属于三相同时切换算法。由优化脉冲模式推导得到磁链矢量，对谐波磁链矢量偏差的幅值进行判断即可确定切换时刻。分析方法简单有效，且适用不同类型的优化PWM。