水产品贮运过程中货架期预测的研究进展
2021-08-31王红丽王锡昌施文正王玥科
王红丽,王锡昌*,施文正,周 纷,王玥科
(上海海洋大学食品学院,农业农村部水产品贮藏保鲜质量安全风险评估实验室, 上海水产品加工及贮藏工程技术研究中心,上海 201306)
水产品主要指鱼类、贝类、甲壳类、藻类、海参头足类等产品及其加工品,它们是食品供应的重要组成部分,为人类提供了大量优质蛋白,而且富含人体必需的不饱和脂肪酸及多种微量元素[1-2]。我国是水产品(包括淡水和海水)生产、贸易、消费的大国,2019年我国水产品总产量达到6 480万 t[3]。
新鲜水产品捕捞后经过运输、贮藏等环节才能到达消费者手中,但水产品肉质细腻、营养丰富,具有高水分含量和高蛋白活性等特点,且目前生化和微生物分解机制及水产品低温保藏技术及冷链物流体系相对还不够完善,因此水产品在贮运过程中极易发生蛋白质变性、脂肪氧化、质构特性等品质劣变[4-5]。鲜度决定着水产品品质,而消费者了解其品质主要是通过货架期。货架期指食品在不被消费者接受的情况下可以贮存的时间长度[6-7], 它也可以定义为食品可保持其微生物、物理、化学和感官指标的贮存时间。货架期的预测具有经济、环保的优点,因为它决定了产品的最大商业化时间,同时避免食物浪费[8]。近年来通过建模实现对水产品货架期快速预测和评估已成为该领域的研究热点。
为建立贮运过程中水产品的品质变化模型,研究人员应用已知模型通过系统建模方法确定影响水产品品质的特性指标并进行量化,构建影响水产品货架期各个因素间的预测模型,有助于监测整个贮运过程中水产品的质量和安全状况,更加准确及时地预测流通过程中水产品的货架期[9]。本综述介绍了水产品贮运过程中货架期预测内涵和方法,阐述了货架期预测模型的研究进展,以期为水产品的实时品质控制提供参考。
1 水产品贮运过程中货架期预测内涵
从食品工业的角度来看,货架期是产品在适当的贮藏条件下可以保持其品质的时间。达到货架期终点的食品在感官上可能仍然是可以接受的,而对于消费者来说意味着食品具有不可接受的风味[10]。由于食品体系及变质机制复杂且个体无法满足整体消费者的需求,因此不可能建立一个通用的货架期定义。尽管如此,根据某些主要的腐败变质模式可以预测食品的货架期。准确的货架期预测和计算产品在特定条件下的货架期能够为产品的运输、贮存、分销策略提供有效依据。
水产品贮运过程中货架期预测模型实际上是集食品科学、物理、化学、微生物学、数学和计算机科学等多个学科发展起来的技术,对水产品的品质进行预测,通过较低的成本对水产品质量和安全实现快速评估和预测,从而可为水产品的加工和销售提供理论指导依据[11]。
水产品贮运过程中品质变化通常是理化反应与微生物共同作用的结果,此过程会受到温度、水分、气体环境等因素的影响。水产品品质变化机理及货架期模型的研究思路如图1所示[12]。货架期预测模型实际是使用数字算法,选择敏感的、关键的水产品品质指标,基于物理、化学或微生物学的相关原理研究其变化规律,进而研究水产品品质的整体变化规律,实现货架期的预测[13-14]。Tsironi等[15]研究了冷藏过程中金头鲷片相关品质(色泽、总挥发性盐基氮(total volatile basic nitrogen,TVB-N)含量、感官评价等)变化并进行了动力学建模。吴行印等[16]比较了不同贮藏温度下小黄鱼感官评价、TVB-N含量、菌落总数及K值(鲜度指标)等的变化,并运用Arrhenius方程对TVB-N含量、菌落总数和K值建立动力学预测模型。

图1 水产品品质变化机理及货架期模型的研究思路[12]Fig.1 Mechanism underlying quality change and strategy for shelf-life modeling of aquatic products[12]
2 水产品贮运过程中货架期预测的研究方法
货架期通常由两种稳定性测试程序来预测:等温法和货架期加速实验(accelerated shelf life testing,ASLT)法。产品开发阶段的货架期测试全过程[17]如图2所示。早期ASLT采用两步等温法,即在压力过高的环境中(如高温、低pH值和高水分活度)进行等温贮藏实验,根据加速因子和降解速率之间的关系利用方程通过外推法来预测特定贮藏环境的货架期[18],但预测数据具有不确定性。ASLT法逐渐发展到非等温方法,此方法尽量避免外推,充分利用Q10模型、Ea(活化能)等参数将加速贮藏和Arrhenius方程结合应用于货架期预测。目前ASLT法通常是等温和非等温法相结合,等温实验所得模型进行了变温实验,通常将动力学方程与Arrhenius方程结合共同评价货架期。

图2 产品开发阶段的保质期测试策略[17]Fig.2 Shelf-life testing strategy for different product development stages[17]
温度是最常用的加速因子。水产品尤其是冷冻品品质损失动力学反应速率较慢,ASLT使用苛刻的实验条件将加速实验结合动力学模型在短时间内协助研究品质损失,进而进行货架期预测[18]。研究表明,-5 ℃是稳定冷冻肉制品ASLT的安全测试温度。然而,腐败变质可能在达到消费者可接受时间之前发生,因此也有研究推荐 -8 ℃作为冷冻品稍高的加速温度。由于-20 ℃下水产品的货架期较长,因此在足够短的时间内发生可测量变化的温度限制在-15~-5 ℃范围内[19-20]。近年来对冷藏温度下ASLT的研究较多,但用于冻藏条件下预测模型较少,可能由于冻结伴随着相变,因此将相关的温度范围限制在凝固点以下。货架期预测在冷冻水产品中的研究较少,而在冷冻果蔬等产品中均有报道[21-22]。等温法 和ASLT法优缺点的比较如表1所示。Li Deyang等[23]采用加速贮藏实验结合Arrhenius方程,预测了热风干燥和冷冻干燥南美白对虾的货架期,此外,在干蛤的货架期 预测[24]中也有相关报道,但并非针对于冷冻水产品。Tsironi等[25]研究了可变贮藏条件对冻虾货架期品质的影响,为了确定其在实际冷链中适用性,对所建立的模型在温度波动的情况下进行了验证。

表1 等温法和ASLT法的优缺点比较[21]Table 1 Comparison of advantages and disadvantages between isothermal method and ASLT method[21]
3 水产品贮运过程中货架期预测模型的研究进展
水产品贮运过程中货架期预测模型主要分为基于温度的货架期预测模型、基于化学反应动力学预测模型等5 种,近年来水产品中几种常见的货架期预测模型如表2所示,进而对货架期模型的分类及国内外研究进展分别进行详细阐述。

表2 水产品货架期预测的主要模型Table 2 Major prediction models for the shelf life of aquatic products

续表2
3.1 基于温度的货架期预测模型
3.1.1 Arrhenius方程
水产品贮运过程中品质劣变速率受多种因素的影响,其中温度对其影响最大。Labuza等通过Arrhenius关系式确定了食品的腐败变质速率与温度的关系,其一般反应式如式(1)[43]所示。

式中:B表示品质指标值;t表示时间;k表示品质速率常数;n表示反应的动力学级数。
不同反应的动力学常数应根据食品品质衰变的指标来描述其品质变化规律[44]。描述化学反应的最常用基准模型是Arrhenius方程,它表示温度对水产品品质指标的影响,其方程式如式(2)所示。

式中:K0、Ea、T、R分别表示指前因子、 活化能/(kJ/mol)、绝对温度/K、摩尔气体常数(8.314 4 J/(mol·K))。
Arrhenius方程描述温度与反应速率的关系,目前主要集中研究化学反应动力学与Arrhenius方程结合使用,其形式简单、适用性比较强,且只考虑温度的变化。由于微生物生长是一个生物化学过程,因此在一定的温度范围内将遵循Arrhenius方程。如果所有其他生态因素保持不变,生长速率的温度依赖性则可用总活化能来表征。缺点是适用于较小温度范围水产品货架期的预测,温度范围较大时准确度降低。雷志方[45]、Li Weiqing[26]等分别探究了金枪鱼、真空包装扇贝贮藏的货架期预测模型,冻虾[25]、 草鱼[46]等的货架期预测模型也被广泛研究。Arrhenius方程为水产品品质预测和优化提供了一个很好的途径。然而,有研究证明Arrhenius方程不适合预测鲫鱼、鲤鱼等鱼类在低温贮藏过程中腐败后期的变化[31,47]。
3.1.2Q10模型
Q10模型是根据Van’t Hoff经验规则衍生而来,是指当温度升高10 ℃时,反应速率为原来速率的倍数或货架期的变化率[48]。Q10模型需借助Arrhenius方程求出Ea,且预测温度范围较小,因此Q10模型预测范围有限[49]。Q10模型可通过公式(3)表示,一般与Arrhenius方程结合使用。
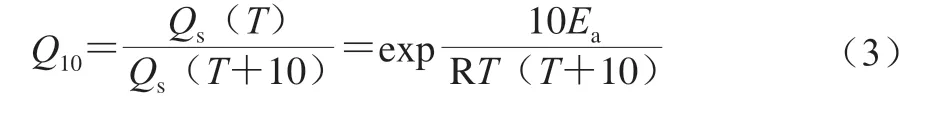
式中:Qs为水产品的货架期寿命,Q10的大小取决于食品系统、温度和绝对范围。
冷冻食品Q10值一般在2~20之间[50]。Q10模型实际是一种简单的加速货架期实验方法,优点是不需要考虑反应级数,只侧重于温度对货架期的影响,但应用范围较窄,且仅适用于较小的温度范围,而导致其预测精度较低[51],在水产品货架期预测方面应用较少,而在罐头食品相对较多。佟懿等[27]利用电子鼻技术结合理化指标建立了鲳鱼Q10货架期的预测模型。
3.1.3Z值模型
Z值模型侧重于以微生物改变为主的生化变化过程,主要用于基于杀菌效果的罐头货架期分析中,而在水产品货架期预测研究空白,Z值模型预测精度较高[44],通常与Arrhenius方程结合用于货架期的预测,两者都能反映温度与品质速率变化的关系[28]。Z值模型克服了水产品贮运过程中实际微生物的生长并非理想的状态,而Arrhenius方程中微生物的生长默认为理想状态,因此Z值模型常用来进行杀菌致死预测[52],但此模型仅适用于较小温度范围水产品货架期预测,因此应用相对较少。
基于温度的货架期预测模型能够预测不同温度下水产品品质变化规律,可为减少生产、贮运过程中环境温度变化导致的腐败变质提供参考。
3.2 基于化学反应动力学的预测模型
化学反应动力学模型的建立是基于水产品相关品质变化会受到化学反应的影响,忽略了环境因素的变化,而在贮运过程中温度、湿度、微生物、pH值、气体环境等都会影响化学反应速率,只考虑水产品贮运过程中理想状态下的变化[53],其应用范围有一定局限性且依赖刚性模型,但品质变化规律可为贮运过程中水产品品质提供参考[54]。
水产品化学反应动力学模型的建立一般分为3 步:1)根据样品性质设定贮藏温度梯度,依据不同温度的贮藏时间点对相关指标进行测定,其变化规律则通过零级或一级反应方程进行描述;2)根据敏感指标进行曲线拟合分析,从而获得Arrhenius方程中未知参数的值,同时验证模型的有效性确定水产品变温条件下品质变化动力学模型;3)结合贮藏实验货架期终点品质指标值,实现对水产品剩余货架期的预测[12]。水产品在贮运过程中的质构、色泽、营养风味等变化的反应规律大多数遵循零级、一级或二级化学反应动力学[54],其中一级反应动力学应用最广泛,在鲫鱼[29]、花蛤[31]等中都有相关研究。
3.3 基于微生物学的预测模型
因为微生物是影响水产品货架期的重要因素,所以微生物生长动力学模型得以广泛应用[55]。水产品微生物学预测模型主要是以特定腐败菌的生长规律为基础,如冰藏海鱼中的腐败希瓦氏菌、冰鲜淡水鱼类中的假单胞菌和二氧化碳、冷鲜鱼类中的发光杆菌[56],具有较高的预测准确度。Whiting等[57]将微生物生长动力学分为初级、二级和三级模型,其中初级模型适用于描述微生物数量随时间变化的关系,常用来建立不同温度下微生物生长预测模型;环境因素(温度、水分活度、pH值等)对微生物生长动力学参数的影响常用二级模型表示;三级模型则是进一步建立在一级和二级模型基础上的应用软件程序,进一步增加了模型的快捷及实际应用功能[58]。 常见的微生物生长动力学模型分类如表3所示。

表3 微生物生长动力学模型的分类及特点Table 3 Classification and characteristics of microbial growth kinetic models
初级模型中Gompertz模型、Baranyi模型和Logistic模型等是最常用的微生物货架期生长预测模型[60]。蓝蔚青等[32]采用修正的Gompertz方程建立了流化冰贮藏 (-1.8 ℃)、碎冰贮藏(0 ℃)、冷藏1(4 ℃)与冷藏2 (10 ℃)条件下鲈鱼的希瓦氏菌与假单胞菌数动态变化,并分别以Belehradek平方根方程和Arrhenius方程建立微生物生长预测模型,为鲈鱼流通货架期的预测提供理论依据。运用Belehradek平方根方程和Rakowsky模型进行微生物货架期生长预测在大西洋鲑鱼[33]、热带咸淡水虾[34]等中也有应用。通过水产品特定腐败菌的生长特性的模拟构建微生物预测模型是目前研究的重点。尽管利用微生物预测模型进行水产品货架期已得到广泛应用,但仍然存在以下问题:1)研究大多数是针对新鲜水产品微生物生长繁殖引起的品质衰变而进行的货架期模型预测,对冻品而言,水产品的品质的劣变主要是由于蛋白质 变性、脂肪氧化水解及冰晶的形成迁移等,但温度波动下的水产品品质劣变又与微生物有较大关系,对温度波动下水产品的货架期则是需要深入研究的方向之一;2)水产品贮运过程中品质劣变通常是多种腐败菌共同作用的结果,仅靠几种特定腐败菌准确性大大降低;3)通过大量数据模拟的微生物建模主要为经验性模型,而数据的来源对微生物货架期预测的准确性和实用性有着较大的影响。
3.4 基于统计学的预测模型
3.4.1 威布尔危害分析法
为了评估食品的品质,研究者使用微生物测试和客观的理化分析方法,最后与感官分析数据相关联,以此提高品质评价的准确性。大多数食品的货架期只能通过观察其发生感官品质劣变或微生物变化所需的时间来评估,样品集内个别单元的损坏率的极端差异表明,对多个样品的感官分析是评价货架期最合理、最简单的标准。WHA是一种图形方法,也称为最大似然法,是由Gacula等提出的运用感官评价手段对相对误差进行模型验证一的种新的货架期预测方法,首次将食品失效时间引入WHA能直接预测水产品的货架期,但仅能处理食品感官实验数据,不能对理化或微生物指标进行分析,且对感官人员的实验技术水平和专业知识要求较高[61],常用于肉制品、乳制品、化妆品等食品货架期的预测。
由于消费者对滋味和气味的敏感性具有主观性,因此需要大量的感官人员来进行统计分析,进而用统计技术来确定所需预测模型的准确性。目前将WHA用于水产品贮运过程中货架期模型的预测研究较少。陈慧斌[35]、 戴阳军[36]等研究了牡蛎速冻、草鱼片微波速冻过程中的危害因素和关键控制点,建立了相应的预防措施。 Aguile等[62]应用WHA模型较好地拟合了4 种冻藏温度下大西洋鲑鱼质构特性及盐溶性蛋白含量。
3.4.2 最小偏二乘法
最小偏二乘法能综合处理和分析数据得到函数关系式从而来确定未知参数的一种基于统计的方法。它能消除随机成分和噪音,通过降低均方误差和提高模型的相关系数来提高预测模型的稳定性[63],通常与快速检测技术(近红外光谱技术、电子鼻分析等)联合共同预测水产品的货架期。
最小偏二乘法因使用过程中已经默认了是线性估计,因此使用具有一定局限性。励建荣等[37]以K值作为鲜度预测的变量,采用偏最小二乘法选取大黄鱼近红外光谱的特征光谱区进行建模分析。张欣欣等[38]通过近红外光谱技术测定了镜鲤的相关鲜度指标,分别用偏最小二乘法和人工神经网络(artificial neural network,ANN)进行预测模型的比较建立。
3.5 基于人工智能的预测模型
3.5.1 人工神经网络
新兴的货架期预测方法ANN是一种模仿生物神经网络 结构和功能的数学或计算模型,主要包括BP-ANN和径向-ANN[59]。通过学习过程在输入和输出变量之间建立有意义的关系,针对非公式化和非稳定性计算结果的信息分析技术,能够处理复杂的、相互关联的过程及线性和非线性回归问题[64]。通过对已知数据的反复学习、网络训练的方式能较好地解决多指标预测问题,具有自学能力,且可同时研究多个环境因子,为了实现数据的高度拟合,达到均方误差最小化需要不断修改网络的权值和阈值,已用于加工后的水产品货架期预测[65]。但软件开发费时,用于数据回归的数据量较大,相比于传统动力方程对自身算法过程没办法解释,容易丢失信息,需要进一步完善,一旦开发出来,经过数据的整合和解释说明可以很容易地在程序、电子表格、计算器或硬件设备中得以应用[66]。
近年来ANN在水产品中逐渐得到应用,未来也必将是水产品货架期预测的趋势。与其他预测模型相比,它的优势在于不需要确定品质指标变化规律,能综合多个指标而非单一综合评价,且不需考虑参数之间的关系,从而减少系统误差,通过不断学习从而提高预测的准确性。Siripatrawan等[67]对常压空气和体积比4∶3∶3的二氧化碳、氧气、氮气的混合气体改性空气包装条件下鲍鱼肉从气味、色泽、外观等感官特征进行评价开发了一种新的新鲜指数法,用于ANN算法以新鲜度指数校准生化和仪器分析,该神经网络能够将生化分析和仪器分析与新鲜度指标相关联。Shi Ce等[39]建立了BP-ANN,可作为预测鲢鱼在0~3 d热处理期间肌苷酸损失的潜在工具。Liu Χiaochang等[64]基于运用Arrhenius和ANN两种模型对不同贮藏温度下虹鳟鱼肉的感官评价、电导率和K值等指标的变化进行了比较分析,结果表明与Arrhenius方程相比,ANN模型能更准确地预测虹鳟鱼的货架期。
3.5.2 TTT理论和TTI的研发
早期冷冻贮藏实验特点是数据密集冗杂且缺乏组织性数据结果,导致结果较难比较分析,因为使用了不同的温度和标准来保持食品的品质,而关于初始品质、加工过程和包装(initial product, process and packaging,3P) 的数据往往不足。van Arsdel[68]在1957年对冻结食品(水果、蔬菜、家禽等)在不同的冻藏温度下选择各种指标进行了不同时间长度的测试,即TTT,也称为“Albany”系列实验,经过归纳总结揭示了冷冻食品3P与TTT的关系,对食品冻藏具有实际理论指导意义。上述货架期预测模型多数是在恒定温度下,TTT理论可用于实际水产品贮运过程中温度波动条件下货架期预测,因为冻结过程中品质下降是累积的、不可逆的,品质累积下降程度和剩余货架期可根据TTT曲线计算。TTT理论为计算水产品品质下降提供了最简便的方法,且可用于温度波动下水产品货架期的预测,曲线的绘制需要耗费大量的人力和物力,且需要对贮运过程中水产品的温度进行实时监控。
冷藏和冻藏水产品在贮运过程中需要对其从生产到消费整个过程的品质和安全进行持续监控,因此智能包装系统应运而生,它可以提供有关食品品质的直接信息(如新鲜度指示器)和间接信息(如时间-温度积分器/指示器)。TTI是一种可以跟踪从制造点到零售店的陈列架整个分销过程所经历的累积时间-温度分布函数设备或标签。它是基于机械、化学或酶系统不可逆转地发生变化,通过黏附在食品包装上颜色变化或者机械变形等多种不可逆变化原理直接显示水产品贮运过程中的剩余货架期,而颜色的变化与温度条件直接相关[69]。TTI反应速率常数通常遵循Arrhenius理论,常用于新鲜、易腐水产品货架期预测,具有方便、智能优势,为生产者、运输者以及消费者提供了准确检测和评估,但制作成本较高且需要智能精确化操作[70]。Taoukis等[41]报道了地中海金枪鱼天然菌群的温度行为,用Arrhenius和平方根函数模拟了菌群的最大生长速率与温度的关系,对来自相似 贮藏实验的几种TTI的响应进行了建模。Tsironi等[42]研究应用副溶血性弧菌和创伤弧菌在牡蛎中生长的预测模型,并设计了具有反应动力学的酶促TTI智能标签,用于指示弧菌的生长潜力。近年来水产品贮运过程中货架期预测的方法应用对比如表4所示。

表4 水产品贮运过程中货架期预测的方法应用对比Table 4 Comparison of various methods for shelf life predictive modeling of aquatic products during storage and transportation
4 结 语
在水产品贮运流通中过程中,基于消费者认可度的货架期才有实际意义,从这个角度讲,水产品的货架期不仅取决于水产品自身,还取决于消费者的感官评价。水产品贮运过程中货架期模型的建立能更好地对水产品的品质进行预测,从而对水产品贮运保鲜提供理论支撑。
目前,大多数水产品贮运过程中货架期预测主要基于特定的温度,而在实际贮运过程中,温度波动对水产品货架期影响较大,应试图寻找能实时监测水产品新鲜度的有效方法来量化水产品的品质,以此提高预测模型的准确性;货架期一级和二级模型应用较广泛,研究应将其与三级模型进行结合,建立更加准确、方便、快捷、完善的货架期监控预测模型;不同货架期模型、快速检测技术结合动力学方程[77-78]、智能包装 系统[79-81]、新传感器的研制等都为水产品新鲜度的判断及货架期预测提供了新思路。
