挖掘教材资源 培养学生数学素养

宛新民

摘要：数学素养是现代社会每一个公民应该具备的基本素养。培养和提升学生的数学素养，应该落实在教师每一堂课的教学活动中、每一道习题的解答中。充分有效地挖掘教材资源，只要方法得当，就能激发学生的学习兴趣和主动探索的热情。这不仅可以提高学生的学习效率，减轻学生课业负担，还能达到有效提升学生的数学素养的目的。

关键词：教材资源  数学思想方法  数学素养

提升学生的数学素养是义务教育阶段数学教育的一项基本任务。如何培养和提升学生的数学素养？大部分教师采用简单粗暴的题海战术，不仅占据了学生大量的课余时间，增加了课业负担，还得不到理想的教学效果，甚至适得其反，让孩子产生厌学情绪，成绩一落千丈。要摆脱这样的困境，除了引导学生自身探索、总结外，更应该将培养学生素养的教育理念落实在教师的每一堂课的教学活动中、每一道习题的解答中。其中，有效地开发和利用教材资源，只要方法得当，就能激发学生的学习兴趣和主动探索的热情，不仅可以提高学生的学习效率，减轻学生课业负担，也能达到有效提升学生的数学素养的目的。以下就是我在教学实践中的一则实例。

一、发现问题

人教版九年级数学下册第二十七章“相似”的复习题中，有这样一道题：如图1，AD⊥BC，垂足为D，BE⊥AC，垂足为E，AD与BE相交于点F，连接ED。你能在图中找出一对相似三角形，并说明相似的理由吗？

显然，这道习题并不复杂，但教材为了降低难度，只提出“找出一对相似三角形，并说明相似的理由”的问题。同时，这也是一道开放性的问题，为学生的回答提供了多种可能。不同的学生从不同的角度回答给出不同的答案。数学素养好的学生就会主动探究各种可能情况，而一般的学生只要找到一种答案就万事大吉了。作为教师，我们应该有意识地引导学生进行探究，从而锻炼学生的数学思维能力，促使他们领悟数学思想方法、提升数学素养。

在实际教学中，我根据学生提出的不同答案，因势利导地提问：图中共有多少对相似三角形？你能都找出来，并说出理由吗？结果发现，学生马上来了兴趣，都积极地寻找起来，可是能把所有相似三角形都找出来的同学并不多。究其原因，我认为主要是他们的思想方法不对，一味盲目地猜测而不去寻找规律，只能得到片面的结果，归根结底还是他们的数学素养问题。

二、解决问题

为了帮助学生解决问题，我引导学生先回顾复习一下前面学过的相似三角形的判定方法，有意识地运用如下的数学思想和方法来进行分析解答。

（一）建立模型

首先，回顾预备定理即“平行于三角形一边的直线和其他两边相交，所构成的三角形与原三角形相似”。有下列两种情形：如图所示，图2、图3中DE∥BC，则△ABC∽△ADE，我们分别称为“A”型和“S”型，这样就建立了数学模型。

（二）运用类比思想体会特殊与一般关系

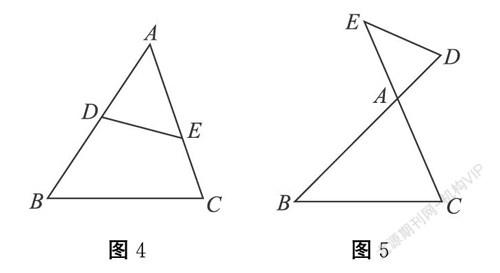
在上述模型的基础上，我们再通过类比全等三角形的判定方法分别得到：三边成比例的两个三角形相似（类比SSS）;两边成比例且夹角相等的两个三角形相似（类比SAS）;两角分别相等的两个三角形相似（类比ASA或AAS）三个判定定理。在判断两直角三角形相似时还有斜边和一条直角边成比例的两直角三角形相似（类比HL）等。再拓展一下，很容易得到下面的两种情形，若圖2、图3中的DE与AB不平行时，如下图所示：

图4的△ABC与△ADE中∠A为公共角，且∠B=∠AED，则△ABC∽△AED;图5的△ABC与△ADE中若∠B=∠E，又对顶角∠BAC=∠DAE，所以△ABC∽△AED。这两种情况我们分别称为反“A”型和反“S”型，从而又建立了两个判定相似三角形的模型。

（三）分类的思想

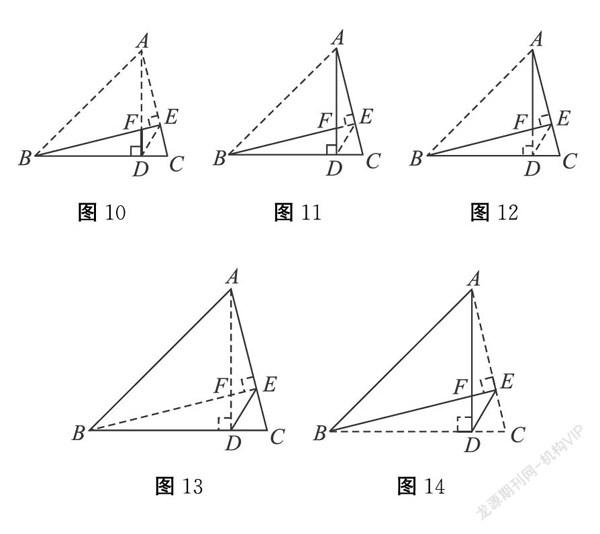
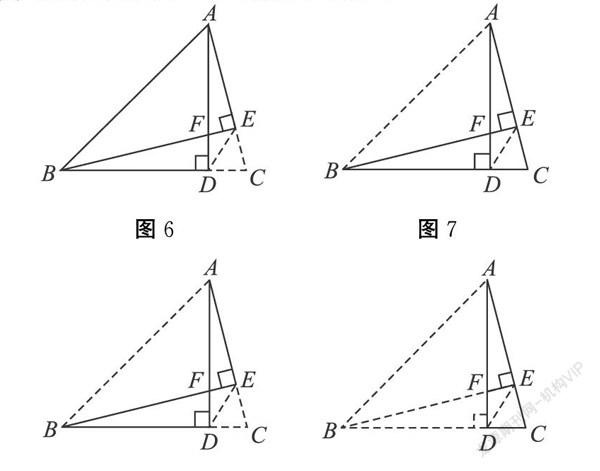
现在，我们再回到开始的习题，如何正确地找出图中所有相似三角形呢？我们从题目的已知条件入手，题中有两个垂直，可以很容易想到直角三角形，那么，我们就从直角三角形开始分析。图中有哪些直角三角形呢？它们相似吗？这就要求我们能从复杂的图形中找到我们所需要的简单图形或模型，我们可以看出图6～12的以下情形：

从中不难分析出直角三角形相似的情况。除此以外还有非直角三角形的情形，如图13、图14中△ABC∽△EDC，△ABF∽△EDF

再回过头来看一下可以发现，图9、图10、图13都属于反“A”型，图8与图14属于反“S”型。根据模型可以在复杂的图形中找到需要的简单图形，从而解决问题。

三、归纳反思

在上述寻找相似三角形并说明三角形相似的理由的过程中，我们首先要能从复杂的图形中找出简单的基本图形，体现了模型思想及由简单到复杂，再由复杂到简单的认识规律及数学思想。

在找相似三角形时，从三角形的形状来看分为直角三角形和非直角三角形两类;在直角三角形中又有相似和不相似两类;从两个相似三角形的位置来看分为反“A”型、反“S”型及其他类型。在说明两三角形相似的理由时，分为有公共锐角或对顶角的直角三角形（两角分别相等的两个三角形相似）、没有公共锐角或对顶角的直角三角形及两个非直角三角形等类型，体现了分类的数学思想，可以培养学生形成缜密的思维习惯。

我们还采用了类比的思想区分“A”型与反“A”型、“S”型与反“S”型等基本几何图形。

四、拓展应用

解决问题以后，我们再顺势提出：如果△ABC是等腰三角形（有AB=BC或AC=BC两种情形）时，其他条件不变，情况又会如何呢？如果△ABC是等边三角形时，其他条件不变，情况又会如何呢？也就是从一般情况看特殊情况，可以引导学生进一步去思考探究。

可见，充分有效地开发利用教材资源，不仅可以激发学生的学习兴趣，提高学习效率，减轻课业负担，也能达到有效提升学生的数学素养的目标。